Компьютерное моделирование активной фазированной антенной решетки

ПАНТЕНКОВ Д.Г.

ГУСАКОВ Н.В.

GUSAKOV Nikolay Vasilievich – deputy general designer at RSC Energia, Candidate of Science (Engineering)

В активной фазированной антенной решетке (АФАР) каждый ее элемент или группа элементов имеют свой собственный миниатюрный микроволновый передатчик, обходясь без единой большой трубки передатчика, применяемой в радарах с пассивной фазированной решеткой. Каждый элемент АФАР состоит из модуля, который содержит щель антенны, фазовращатель, передатчик и часто также приемник [1].

По сути АФАР является радиотехнической системой, в которой радиопередающее устройство и высокочастотный приемник интегрированы в антенную решетку в виде распределенной структуры, включающей в себя в качестве основных узлов приемопередающие активные модули.

В связи с этим при разработке АФАР необходим комплексный подход, учитывающий взаимное сопряжение электродинамических свойств излучателей антенного полотна и радиотехнических характеристик приемопередающих антенных модулей при различных видах сигналов, краевые эффекты, технологические и временные дестабилизирующие факторы отказов модулей.

Существенное повышение качества, надежности, устойчивости, оперативности радиосвязи, увеличение ее дальности и объемов передаваемой информации связаны, прежде всего, с разработкой в последние десятилетия систем спутниковой связи. В мобильных и космических радиокомплексах все шире применяются АФАР, позволяющие реализовывать многофункциональный режим работы и удовлетворять возрастающие требования к необходимым энергетическим и массогабаритным характеристикам связной аппаратуры [2].

Поскольку энергоресурсы мобильных пунктов, как правило, ограничены, поддержание высокого потенциала АФАР в секторе сканирования связано с минимизацией всех потерь как в передающем тракте, так и на участке радиолинии. Отсюда возникают следующие основные требования к АФАР:

• •    максимальное значение коэффициента эллиптичности поля излучения и минимизация его изменения в секторе сканирования;

• •    минимальные потери, обусловленные рассогласованием излучателей при сканировании;

• •    устойчивый режим работы антенных модулей АФАР при изменении нагрузки, вызванном взаимодействием излучателей и краевыми эффектами.

Выполнение перечисленных требований возможно лишь путем оптимизации параметров АФАР с учетом всех факторов, влияющих на ее работу [3–5].

Развитие космической техники предопределило широкое использование искусственных спутников Земли, находящихся на геостационарной орбите (ГСО) или высокоэллиптических орбитах (ВЭО), в качестве ретрансляторов в линиях связи.

К антенным системам (в том числе АФАР) космических аппаратов (КА) связи предъявляется ряд специфических требований:

• •    обеспечение высокого коэффициента усиления антенны (не менее 40 дБ) из-за большой удаленности КА от абонентских станций на земной поверхности (для ГСО расстояние составляет порядка 35 800 км, для ВЭО – до 40 000 км в апогее), что приводит к большим потерям на трассе распространения (затуханию полезного сигнала, зависящего от частоты излу-чения/длины волны излучения и от расстояния передачи информации);

• •    точность установки луча ретранслятора не хуже 0,05°, что накладывает весьма жесткие требования к системе стабилизации положения КА;

• •    реализация заданных законов амплитудно-фазового распределения по полотну сканирующей АФАР.

При этом активная фазированная антенная решетка космического аппарата должна формировать диаграмму направленности специальной формы, позволяющую облучать одни районы земной поверхности, не затрагивая других, а также обеспечивать устойчивость к воздействию преднамеренных и непреднамеренных помех и возможности перехвата излучения. Известными схемами построения антенных систем спутников связи являются зеркальные антенны с облучателем в виде АФАР.

Постановка задачи

Необходимо обосновать потенциально возможные технические характеристики АФАР для различных диапазонов частот в зависимости от габаритов антенно-фидерной системы, шага между элементами решетки и т.д., получить конкретные значения и обсудить полученные результаты на предмет решения целевой задачи подвижной спутниковой связи с борта КА.

Математический аппарат расчета основных технических характеристик АФАР

Активные фазированные антенные решетки описываются в основном теми же параметрами, что и другие классы антенных систем: диаграммой направленности, шириной ее главного лепестка, уровнем боковых лепестков, коэффициентом усиления (КУ), коэффициентом направленного действия, коэффициентами отражения элементов, и имеют те же характеристики.

Помимо этого добавляются новые энергетические характеристики, отражающие специфику АФАР: потенциал П и удельная спектральная плотность мощности шума Q .

Для передающей АФАР потенциал равен

П = СаПУ = КУ Р^,        (1)

где G _a — коэффициент усиления активной фазированной антенной решетки (численно равен произведению коэффициента полезного действия на коэффициент направленного действия); P ₀ — мощность излучения единичного излучателя; N _e — количество единичных излучателей; П _Σ — суммарный потенциал всех единичных излучателей.

Для приемной АФАР удельная спектральная плотность мощности шума

^ V^эф’             (2)

где h _ш — спектральная плотность мощности шума на выходе АФАР; S _эф — эффективная поверхность антенны.

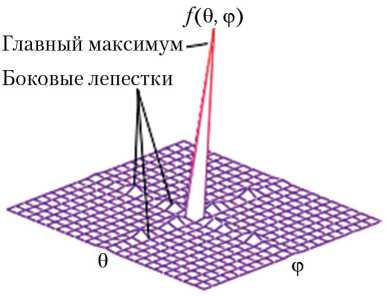
Трехмерная диаграмма направленности АФАР ƒ(θ, ϕ) в общем случае имеет вид где ивх, ивых, iвх, iвых — напряжения и токи на входе и выходе антенного модуля соответственно; e — нормированный вектор; Fвх, Fвых — нелинейные в общем случае интегродифферен-циальные линейно независимые операторы, описывающие активный элемент; Lвх, Lвых — линейные интегродифференциальные операторы, описывающие входные и выходные цепи активного элемента (вакуумной лампы, биполярного или полевого транзистора) и определяемые системой уравнений вида

L = У,ак ^—+Lb^Udt",

М            N                     x 7

l = TXn—^TX\Hdt\

BbIX dtm где R, F, n, m — индексы размерности операторного пространства; a, b — весовые коэффициенты.

Компьютерное моделирование активной фазированной антенной решетки

M

MN

sin \M ud^svtx 6 cos ф)/Х] sin [n ^_r(sin 0 cos tp)/X]

sin [Ж ^(sin 9 sin cp)/X] sin [л rf (sin 9 sin ф)/Х]

где M — количество излучателей по длине полотна антенной решетки; N — количество излучателей по ширине полотна антенной решетки; d_x — расстояние между излучателями в азимутальной плоскости; d_y — расстояние между излучателями в угломестной плоскости; λ — рабочая длина волны излучения; θ — азимут; ϕ — угол места.

Оптимальный выбор размеров антенной решетки выбирается согласно аналитической зависимости вида

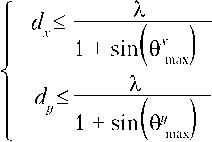
где θ ^x _max , θ ^y _max — максимальные углы раскрытия диаграммы направленности в азимутальном и угломестном направлениях соответственно.

Активный модуль АФАР во временной области можно описать следующей системой уравнений в операторной форме вида

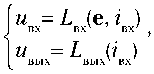
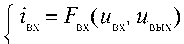
i =F (u ,u ) вых вых^х вх⁷ вых⁷

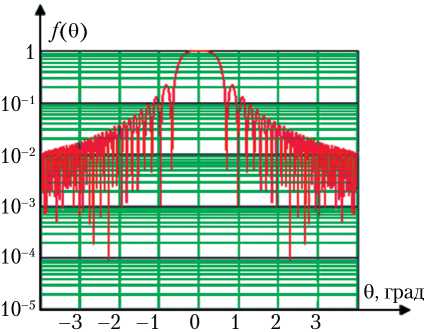
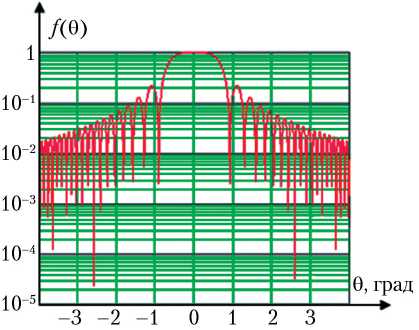
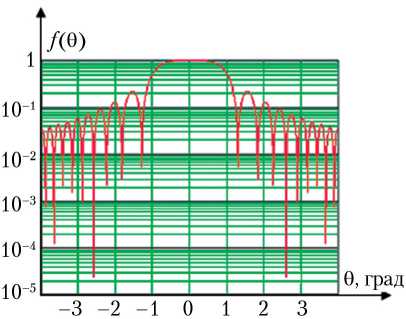
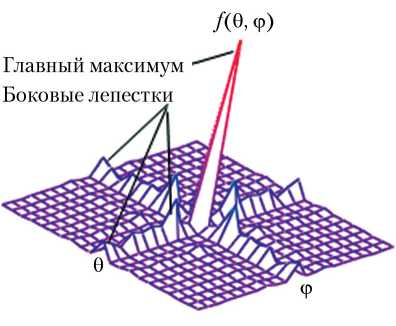
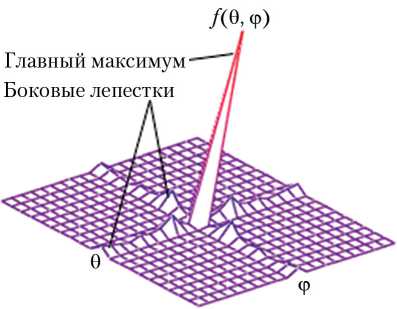
Компьютерное моделирование проводилось для АФАР размером 16 × 16 м на частотах 3, 10, 20 и 25 ГГц. Общее количество элементов антенной решетки составило 16 384 элемента ( M = 128 элементов в азимутальной плоскости и N = 128 элементов в угломестной плоскости). Расстояние между элементами d_x = d_y = 0,1 м. На рис. 1, а, б, в представлены двухмерные диаграммы направленности АФАР в азимутальной (угломестной) плоскости на частотах 20, 10 и 3 ГГц соответственно. В силу симметричности конструкции активной фазированной антенной решетки диаграммы направленности в азимутальной и угломестной плоскостях совпадают. На рис. 2, а, б, в представлены трехмерные диаграммы направленности по двум параметрам (азимуту и углу места) на частоте 10 ГГц АФАР размером 128 × 128, 160 × 160 и 200 × 200 элементов соответственно (шаг между элементами во всех случаях одинаковый, равен 0,125 м).

Моделирование основных характеристик активной фазированной антенной решетки позволяет определить (проанализировать) на этапе проектирования основные характеристики АФАР: минимальную ширину основного луча (важна при формировании многолучевой диаграммы направленности), уровень боковых лепестков (характеризует конструктивную грамотность исполнения АФАР), направленные свойства активной фазированной решетки в целом.

а)

б)

в)

Рис. 1. Двухмерные диаграммы направленности АФАР

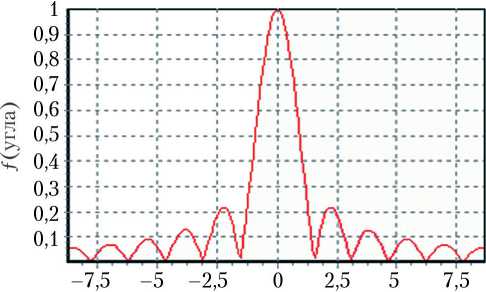
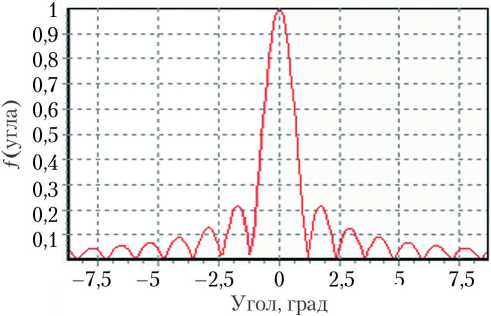
Аналогичное моделирование целесообразно проводить не только в пакетах математического анализа (MathLab, MathCad, Mathematica), но также и численным методом путем написания программ на языке высокого уровня (Borland Delphi, C Sharp, Python) . На рис. 3, а, б, в, г представлены диаграммы направленности в азимутальной (угломестной) плоскости, полученные численным методом в пакете Borland Delphi как суперпозиция всех единичных излучателей для решетки размером 128 x 128 элементов (шаг решетки составляет 0,125 м) на частоте 3, 10, 20 и 25 ГГц соответственно.

Результатом численного моделирования диаграммы направленности АФАР является обоснование технической реализуемости формирования минимального угла в зависимости от частотного диапазона при организации подвижной спутниковой связи.

Для электродинамического моделирования АФАР целесообразно использовать один из нескольких ведущих прикладных пакетов: CST Microwave Studio, HFSS, Microwave Office (возможно, но, как показывает практика, трудоемко и нецелесообразно, написать собственное программное обеспечение для моделирования конкретного типа антенной системы с интересующими граничными условиями и характеристиками, а также смоделировать воздействие окружающей среды на АФАР).

а)

б)

в)

Рис. 2. Трехмерные диаграммы направленности АФАР

Угол, град

Пакет электродинамического моделирования CST Microwave Studio позволяет проводить оптимизацию решетки по критериям направленности и эффективности. CST Microwave Studio имеет опцию для задания геометрических параметров АФАР.

На рис. 4 представлены структура панели АФАР и исходные данные для ее электродинамического моделирования.

а)

На рис. 5, а, б представлены диаграммы направленности для угла сканирования 30° и для ряда углов сканирования соответственно. На рис. 6 представлена итоговая трехмерная диаграмма направленности АФАР на частоте излучения 3 ГГц.

Необходимо отметить, что компьютерное моделирование позволяет уже на этапе эскизного проекта количественно оценить основные технические характеристики активной фазированной антенной решетки: ширину центрального луча диаграммы направленности, коэффициент усиления, уровень боковых лепестков, коэффициент направленного действия. На основании этих характеристик можно предъявить конкретные требования к геометрическим параметрам АФАР, количеству и мощности единичных излучателей, длине и ширине решетки, шагу между излучателями.

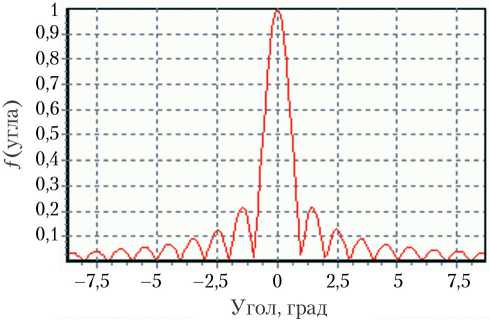
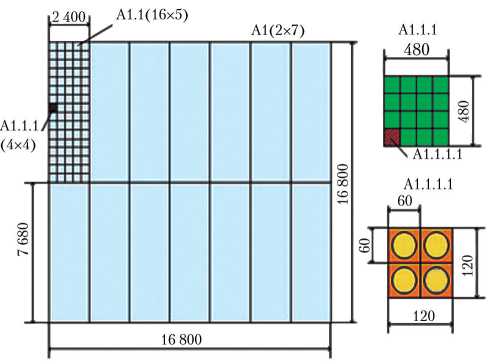
Рис. 4. Структура панели АФАР

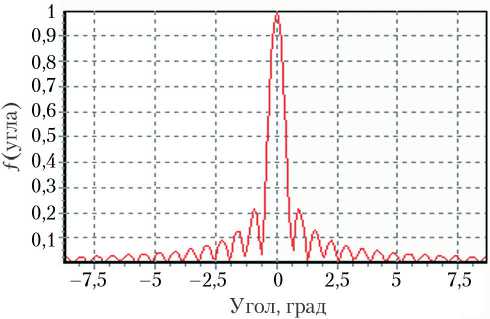
Рис. 3. Диаграммы направленности симметричной АФАР, полученные численным методом

Основные результаты моделирования

Компьютерное моделирование и аналитические расчеты показали, что при эквивалентной изотропно-излучаемой мощности 85 дБВт с борта КА гарантированно решается целевая задача связи на территории РФ, в этом случае плотность потока мощности на входе земной станции спутниковой связи составит не менее минус 84 дБВт в полосе сигнала (ширина диаграммы направленности АФАР в этом случае составит не более 0,7 х 0,7°).

При увеличении ширины диаграммы направленности АФАР до 1 x 1° плотность потока мощности составит минус 90 дБВт, при 1,5 x 1,5° — минус 98 дБВт, при 2,5 x 2,5°— минус 110 дБВт, при 5 x 5° — минус 125 дБВт, при 7 x 7° — минус 138 дБВт. Как показывает практика, на входе земной станции спутниковой системы связи (например, «Ямал-300») требуется уровень плотности потока мощности не менее 158 дБВт.

Таким образом, АФАР с передатчиком 85 дБВт гарантированно решает целевую задачу обеспечения подвижной спутниковой связи как одним глобальным лучом, так и множеством лучей шириной 0,7 x 0,7°. Необходимо добавить, что преимуществом формирования множества лучей по сравнению с глобальным лучом с одной АФАР являются: более высокая скорость передачи данных, относительно низкие требования к антенным системам наземных станций, большая помехозащищенность радиолинии, возможность динамического регулирования мощности сигнала в каждом луче.

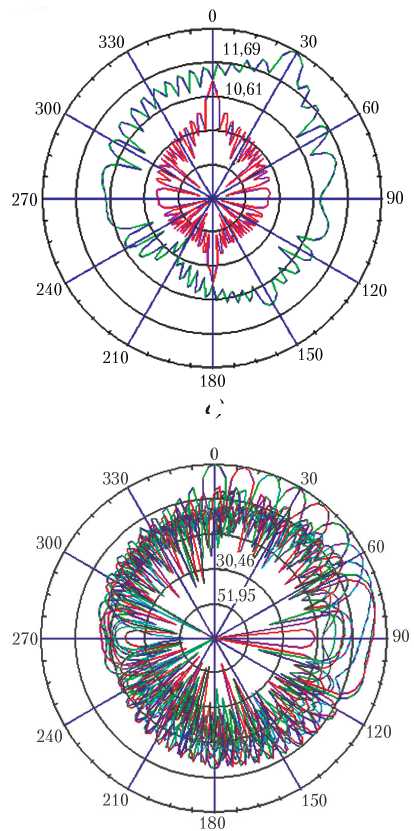
а)

б)

Рис. 5. Моделирование АФАР в полярной системе координат

С энергетических позиций АФАР размером 16 x 16 м способствует обеспечению коэффициента усиления 50 дБ и формированию минимальной ширины центрального луча диаграммы направленности 0,45 x 0,45°, что позволяет формировать локальный луч диаметром 230 км на поверхности Земли.

Трехмерные диаграммы направленности активной фазированной решетки позволяют количественно оценить уровни боковых лепестков в азимутальной и угломестной плоскостях в зависимости от рабочей частоты, шага между элементами решетки и числом элементов в решетке.

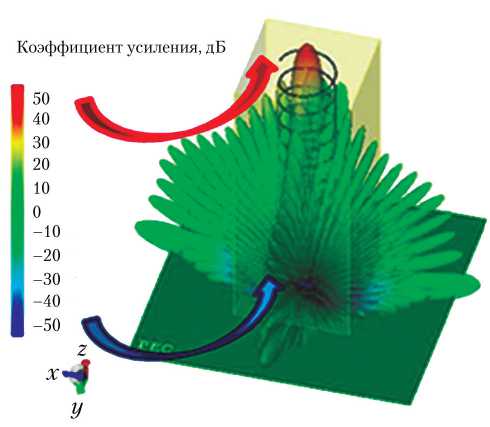
Рис. 6. Электродинамическое моделирование АФАР