Компьютерное моделирование асинхронного электропривода с гидромуфтой

Введение. Гидромуфты (ГМ) нашли широкое применение в силовых приводах ленточных, цепных скребковых и пластинчатых конвейеров, элеваторов, осевых вентиляторов и дымососов, в приводах питательных насосов и газовых турбин, дробилок и мельниц различных типов, роторных экскаваторов, дорожных катков, бетоносмесителей, барабанных сушилок и центрифуг, в составе гидромеханических коробок передач тепловозов, автомобилей, тракторов. Использование ГМ в составе силового привода даёт следующие преимущества:

• •    улучшение статических и пусковых характеристик машины;

• •    защита привода от динамических перегрузок при резкой остановке, например заклинивании рабочего органа машины;

• •    ограничение крутящего момента заданной величиной в режимах пуска и торможения, что предохраняет двигатель, привод и рабочий орган машины от недопустимых перегрузок;

• •    демпфирование и снижение амплитуды крутильных колебаний в приводах, возникающих при работе машины.

Наиболее распространён электропривод с асинхронными двигателями (АД) [1]. В ряде случаев ГМ является здесь связующим звеном между силовым валом АД и приводимого механизма. При этом ГМ обеспечивает плавность разгона механизма передачи энергии и облегчение условий прямого пуска АД на холостом ходу и с нагрузкой.

Эффективным способом анализа динамических процессов, поиска путей совершенствования конструкций является компьютерное моделирование. В связи с постоянным совершенствованием аппаратной части ЭВМ и программного обеспечения не перестаёт быть актуальной задача создания современных инструментов имитационного моделирования в электро- и гидроприводе, в том числе с использованием технологий визуального программирования.

Математическая модель трёхфазного АД. В основу компьютерной модели АД с ГМ положена математическая модель трёхфазной электрической машины в заторможенной системе координат а, Р, Y [2], оси которой совмещены с осями А, В, Сфаз статора. Модель дополнена с целью учёта потерь энергии в стали активными сопротивлениями гм контура намагничивания, включёнными в каждой фазе параллельно главным индуктивностям £р [3]. Уравнения, описывающие модель электромагнитных процессов в АД, представлены ниже.

ит = rjm	d^ + dt	^pa _ active	_£о^.
и* = Г^ф	+ d^. dt '	\$_active	_ yop .
и = г / 5/ 5у	dt	^W „active	r '
			MY
-и = г i
	dt	7з
	dt	V3
	d^ (^
-и = г i	+ —L + -—
	dt	7з

Здесь приняты обычные для математической модели обобщённой электрической машины допущения [2]: каждая из трёх обмоток статора создаёт в гладком зазоре синусоидально распределённую МДС. Коэффициент насыщения магнитной цепи принят неизменным. В выражениях (1) и далее приняты следующие обозначения: и — напряжение, / — ток, t — время, г— активное сопротивление, Ф — потокосцепление, оо — частота вращения. Нижние индексы о, Р, у обозначают принадлежность к соответствующей фазе. Нижний индекс s обозначает принадлежность к стато ру, индекс г— принадлежность к ротору, а индекс р — принадлежность к ветви намагничивания Т-образной схемы замещения АД. /м_йЛУе—активная составляющая тока намагничивания. Детализация составляющих системы (1) приведена в выражениях (2) — (5).

Напряжения и₀ на зажимах ветвей намагничивания фаз:

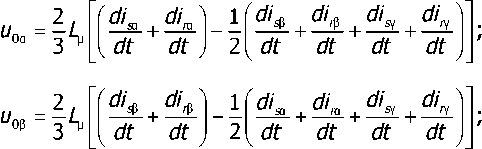
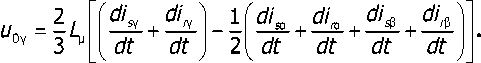
Потокосцепления [1, 2]

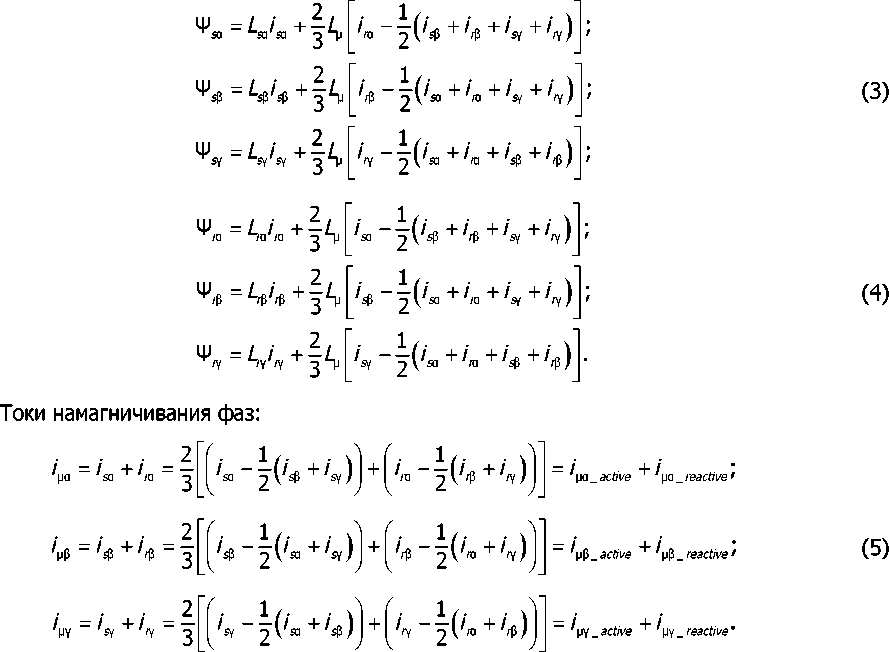
В выражениях (5) / reactive — реактивная (индуктивная) составляющая тока намагничива

ния фазы АД. Для АД типа АЖВ250М23УХЛ2 мощностью ПО кВт активная составляющая тока на магничивания / reactjve составляет приблизительно 5 % от тока намагничивания /м. Это справедли во как в ходе переходного процесса пуска, так и при установившемся режиме.

Уравнение электромагнитного момента АД имеет вид:

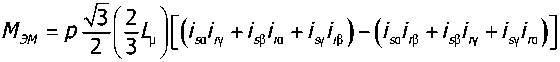
Кинематическая схема механической части привода принята следующая: вал АД — повышающий редуктор — вал насоса — ГМ — вал турбины, к которому присоединена механическая нагрузка. Уравнение движения для вала АД имеет вид:

d^=P_ м dt J ■

эм

м      о насоса ГМ    ^ мехО

р

Ш,о

СО, ,

-kconp.H^r .

Здесь J — момент инерции вращающихся частей ротора, редуктора и насоса с рабочей жидкостью; р — число пар полюсов АД; передаточное отношение jp редуктора — это отношение частоты вращения ротора АД к частоте вращения насоса ГМ jр   <Г /^насоса '

^мнасоса гм/J_P ^— вращающий момент на валу привода насоса ГМ, приведённый к валу ротора АД;

момент механических потерь АД при способе вентиляции электрической машины

«самовентиляция» [4]; р_мех0 — механические потери АД в режиме идеального холостого хода; ш_г0 — частота вращения АД в режиме идеального холостого хода; к_{сощх н}ш, — момент сил сопротивления вращению валов насоса ГМ и редуктора, приведённый к валу ротора АД.

Зачастую необходимо рассчитать энергетические показатели электрической машины в переходном процессе. Для АД при отсутствии электрического питания обмоток ротора мгновенное значение активной потребляемой мощности ^ вычисляется с помощью равенства

Г = ^+1^+1^.

Мгновенное значение реактивной потребляемой мощности Q равно

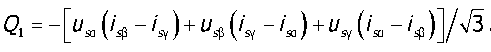
(Ю)

Мгновенное значение полезной мощности Р2 на валу АД

Р м н

(И)

г2 г насоса ГМ [ J р *

Форма уравнений математической модели АД, представленная в трёхфазных координатах о, Р, у, удобна при анализе и сравнении расчётных и реальных значений токов и напряжений фаз АД. Эта форма без дополнительных преобразований и уравнений пригодна для анализа особенностей несимметричных по характеристикам питания или параметрам режимов работы АД.

Компьютерная модель АД. При создании компьютерной модели АД средствами САПР, предназначенной в основном для проектирования и имитационного схемотехнического моделирования электронных и электротехнических устройств, была поставлена задача обеспечения встраиваемости модели АД в единую комплексную модель электрогидродинамической передачи энергии. Получена компьютерная модель, пригодная для описания АД как с короткозамкнутым, так и с фазным ротором. Обмотки фаз могут соединяться по схемам «треугольник», «звезда», иметь любую другую схему соединений между собой или с источником питания. Это достигнуто путём сочетания при построении модели АД двух подходов: схемотехнического для электрической части и метода структурных схем [5] для магнитной и механической частей.

В качестве датчиков и для ввода сигналов в составе модели АД использованы элементы типа ИНУН, ИНУТ, ИТУН. В этих сокращениях: И — источник, У — управляемый, К — напряжение, Т —ток. Например, ИНУТ — источник напряжения, управляемый током. Графическое изображение компьютерной модели фазы А обмоток статора и ротора АД, составленной по (1) — (5), показано на рис. 1, где ^ — индуктивность рассеяния фазы обмотки статора, ^_га — индуктивность рассеяния фазы обмотки ротора. Традиционно параметры ротора приведены к обмотке статора.

ИНУТ1 выполняет роль датчика тока фазы статора /я, аналогично ИНУТ2 — роль датчика тока фазы статора /га. ИТУН1 служит для ввода в схему тока /га — приведённого тока фазы ротора

ИНУН1 вводит в цепь намагничивания фазы напряжение и_Оа. Аналогичную функцию выполняет ИНУНЗ — вводит в цепь обмотки ротора разность ЭДС ветви намагничивания и ЭДС вращения, то есть величину падения напряжения. ИНУН2 является дифференциальным датчиком разности потенциалов на индуктивности . Последующая обработка этого сигнала напряжения путём деления на значение Ц^ даёт производную ^- тока статора фазы. С помощью ИНУН4 выполняется dL аналогичная операция с целью выделения сигнала .

В компьютерной модели, изображённой на рис. 1, использованы сигналы ЭДС ветви намагничивания (12) и ЭДС вращения (13) фаз ротора.

^Оо ^_ ^Оа' а — —// ■ ^сор - ^и0Р'

^Оу = -^0у"

erotQ=^-W>rl^;

^е^=^.-^>г/^', (13)

Активные сопротивления r_serv, указанные на рис. 1, имеют значения порядка 10 МОм. Они введены в служебных целях. Практически не влияя на численные результаты расчёта, указанные сопротивления стабилизируют ход решения (моделирования) за счёт сохранения цепи тока (физический смысл — путь протекания токов утечки). Это особенно важно при дискретном изменении сопротивления цепей питания АД, например при электрическом питании от полупроводникового преобразователя или при обрыве фазы.

Адекватность динамики разработанной здесь компьютерной модели АД подтверждена хорошим совпадением результатов динамического моделирования на эталонных моделях АД (с короткозамкнутым ротором) с номинальными мощностями 1,1 кВт и 4 кВт [1, 6]. Адекватность же статических режимов работы этой модели подтверждена многократными вычислительными экспериментами для известных АД с короткозамкнутым ротором типов НВА-55 (номинальная мощность 55 кВт) и АЖВ250М23УХЛ2 (номинальная мощность ПО кВт) [7, 8]. Результаты этих вычислений удовлетворительно совпадают с данными расчётных записок и протоколов испытаний ОАО «ВЭлНИИ» (г. Новочеркасск) и ОАО «НИПТИЭМ» (г. Владимир). В настоящей работе описаны результаты компьютерного моделирования АД АЖВ250М23УХЛ2 с параметрами и характеристиками, приведёнными в табл. 1.

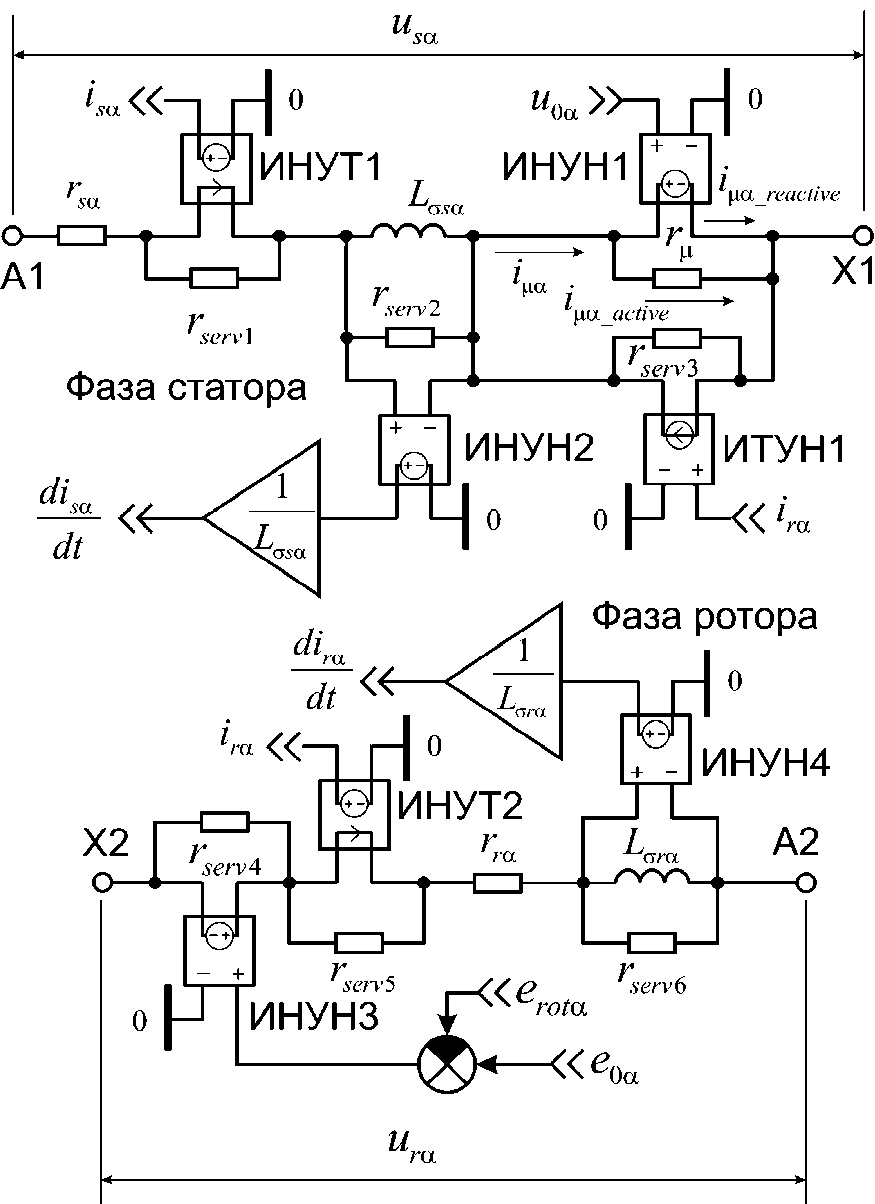
Рис. 1. Графическое изображение компьютерной модели фазы А обмоток статора и ротора АД

Математическая и компьютерная модели ГМ. За основу модели ГМ взята физическая и математическая модель ГМ постоянного заполнения, описанная в [9]. Вращающий момент на валу привода насоса ГМ

Тасоса ГМ = ?(« насосав - toTyp6mJ^Q, где Q— расход рабочей жидкости в ГМ, м3/с, равный _ 900gd2D4 п2

(И)

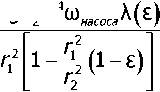
£ — относительное скольжение рабочих колёс ГМ, равное

’турбины

A = f (е) — опытная статическая характеристика ГМ, с²/м.

Таблица 1

Параметры и характеристики АД АЖВ250М23УХЛ2, использованные примоделировании

№ п/п	Наименование параметра	Обозначение параметра в системе координат а, Р, У	Традиционное обозначение параметра в Т-образной схеме замещения АД	Числовое значение	Единица измерения
1	Количество пар полюсов	Р	Р	1	-
2	Активное сопротивление фазы обмотки статора	rs	Л	0,0287	Ом
3	Индуктивность рассеяния фазы обмотки статора	Us	Ui	0,000546	Гн
4	Главная индуктивность фазы	U	U	0,021743	Гн
5	Активное сопротивление цепи намагничивания фазы	Гу	Гу	137,051	Ом
6	Активное сопротивление фазы обмотки ротора, приведённое к статору	Гг		0,013	Ом
7	Индуктивность рассеяния фазы обмотки ротора, приведённая к статору	Ur		0,000355	Гн
8	Момент инерции ротора	Jr	Jr	0,484	КГМ2
9	Номинальное           линейное напряжение статора	-	Uuihom	380	В
10	Частота вращения в режиме идеального холостого хода	СОю	СОю	314,159	рад/с
И	Механические потери в режиме идеального холостого хода	РмеУ)	РмеУ)	740	Вт

Описание других составляющих, участвующих в выражениях (14) — (18), дано ниже в табл. 2.

Уравнение движения для вала турбины ГМ имеет вид

Нгл       М      _ 1с м _ М

^^турбины _ ‘ ‘насоса ГМ ^сопр.Г^турбины ' ‘нагрузки

dt

Г        + /    + / турбины ж.Т нагрузки

В числителе правой части (17): первое слагаемое — вращающий момент на валу привода насоса ГМ (см. (14)); второе слагаемое — момент сил сопротивления вращению валов турбины ГМ и нагрузки; третье слагаемое — вращающий момент на силовом валу механизма внешней нагрузки.

Таблица 2

Значения параметров, использованные при моделировании силовогоэлектрогидродинамического привода

№ п/п	Наименование параметра	Обозначение параметра	Числовое значение	Единица измерения
1	Передаточное отношение редуктора	jp	1/1,2	-
2	Момент инерции колеса насоса	■^насоса	0,5	КГ'М2
3	Момент инерции жидкости насоса	Зж.Н	0,033	КГ'М2
4	Коэффициент, учитывающий увеличение момента инерции ротора АД за счёт приведённого момента инерции редуктора	б	1,2	-
5	Момент инерции колеса турбины	^турбины	0,5	КГ'М2
6	Момент инерции жидкости турбины	Зж.Т	0,033	КГ'М2
7	Момент инерции нагрузки	^нагрузки	2,4	КГ'М2
8	Коэффициент пропорциональности между частотой вращения вала АД сог и моментом сил сопротивления вращению валов насоса ГМ и редуктора, приведённым к валу ротора АД	U •хопр.п	0,0095	-
9	Коэффициент пропорциональности между частотой вращения вала турбины сотурв»™ и моментом сил сопротивления вращению валов турбины ГМ и нагрузки	т •хопр. Т	0,0095	-
10	Ускорение свободного падения	g	9,81	м/с2
И	Плотность рабочей жидкости ГМ	р	850	кг/м3
12	Активный диаметр ГМ	D	0,363	м
13	Малый радиус расчётного круга циркуляции (на средней струйке) колёс ГМ	л	0,054	м
14	Боьшой радиус расчётного круга циркуляции (на средней струйке) колёс ГМ	Гг	0,154	м
15	Ширина кольца выходного сечения канала ведущего колеса ГМ	bz	0,054	м

В (7) момент инерции ./является суммой составляющих

-7 - 5 J + U_Hacoca * З_жнМ ft

I \ nCLULC       Л\ ■! I / / * p

Для оценки (в первом приближении) временных характеристик быстропротекающих дина' мических процессов (например, при ударных нагрузках, вызывающих отрицательные угловые ус коремия порядка 2100 1/с2) последовательно с функцией А = 4 (с), характеризующей статический коэффициент момента ГМ, установленный опытным путём, включено апериодическое звено ^(4), учитывающее запаздывание во времени t реакции силовой гидродинамической передачи на скачок нагрузки, в виде k \ р а^ ?01*

Здесь $)1 — момент ударного нагружения ведомого вала ГМ, с; о — коэффициент, учиты вающий динамику реакции ГМ на нагрузку, 1/с. Нами принято а2 = 2100 1/с2 согласно рекоменда

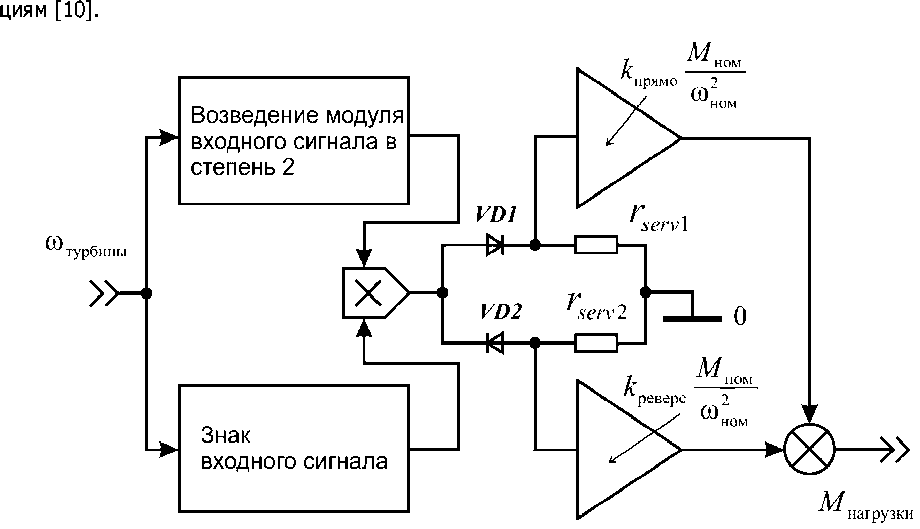
Рис. 2. Графическое изображение компьютерной модели способа формирования реактивного момента вязкого трения

Чтобы придать разработанной здесь модели гидродинамической передачи свойства ГМ со статическим самоопоражниванием (тяговой) [11] с ограничением вращающего момента, передаваемого ГМ, удобно в компьютерной модели использовать нелинейность типа «насыщение».

Для придания свойств ГМ с динамическим самоопоражниванием (предельной) [11], когда опоражнивание или заполнение рабочего объёма ГМ жидкостью начинается при переходе через критическое значение частоты вращения насоса ГМ шНасосакр, можно воспользоваться переходом с одной характеристики A = f (с) на другую в зависимости от степени заполнения ГМ жидкостью. Принимая (для упрощения), что характеристики A = f (с) при любом заполнении ГМ подобны по форме, можно домножать мгновенное значение функции A = f (с), полученное на основной характеристике (при наибольшем коэффициенте заполнения ГМ жидкостью), на текущее значение коэффициента заполнения. Плавное изменение последнего при переходе через шНасосакр получим, полагая процесс опоражнивания или заполнения жидкостью апериодическим с постоянной вре^ мени 0,2—0,3 с. Для этого воспользуемся апериодическим звеном типа кг (Г) в виде:

к     -сгИ^г)                             от

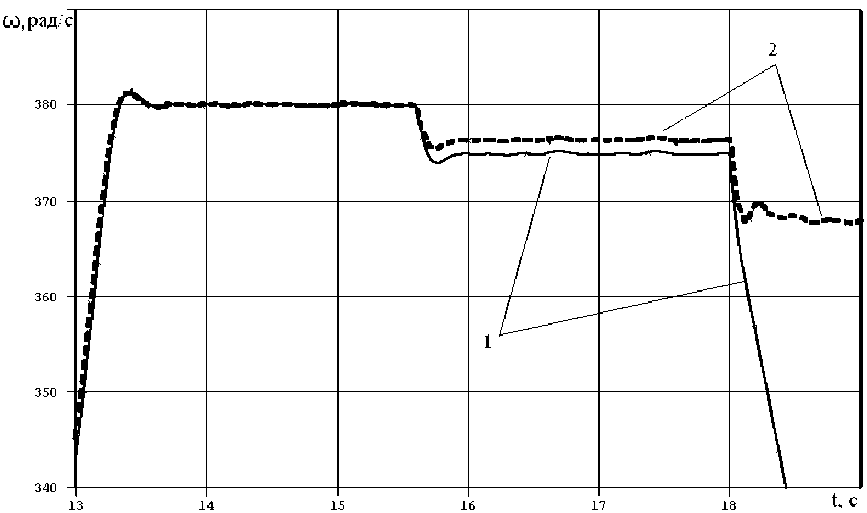
Рис. 3. Результаты компьютерного моделирования динамики привода для ГМ со статическим самоопоражниванием

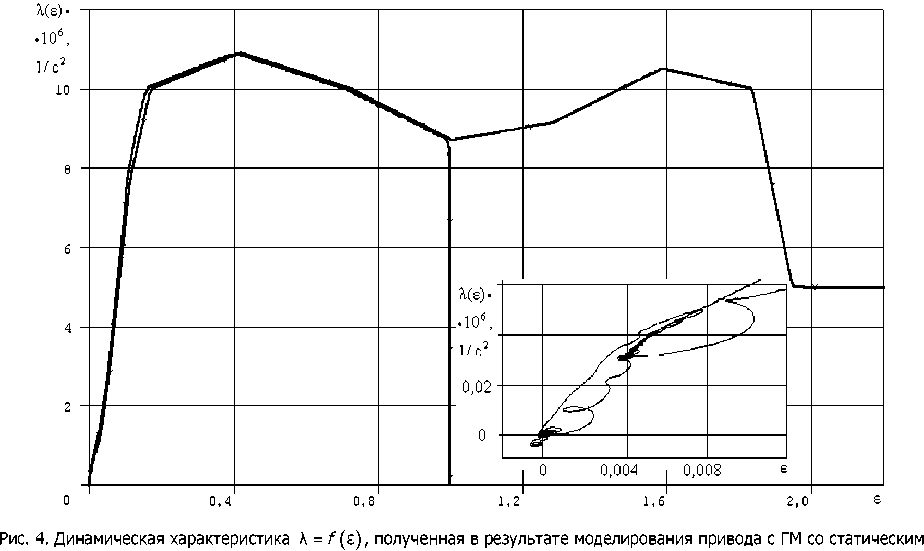
самоопоражниванием при параметрах согласно табл. 1 и 2

Здесь fez — момент достижения значения (й_Насоокр частоты вращения насоса ГМ, с; Р — КО' эффициент, учитывающий динамику опоражнивания или заполнения рабочего объёма ГМ жидко' стью, 1/с. Нами принято 1/3 =0,25 с.

При моделировании М_{нагрузки} в случае ГМ со статическим самоопоражниванием использовался кусочно-постоянный сигнал, изменяющийся ступенчато (холостой ход, нагрузка, перегрузка). В случае ГМ с динамическим самоопоражниванием М_{нагрузки} формировался как сумма реактивного момента вязкого трения (вентиляторного) и момента постоянной величины, действующего только в начальной стадии пуска, то есть до некоторой малой частоты вращения (момент трогания). На рис. 2 показан способ формирования реактивного момента вязкого трения, использованный в описываемой компьютерной модели.

Результаты компьютерного моделирования. Результаты моделирования динамики силового привода показаны для ГМ со статическим самоопоражниванием на рис. 3. Здесь кривая 1 — частота вращения вала турбины «турбины, 1/с. Кривая 2 — частота вращения вала насоса ГМ «насоса, 1/с. Последовательно показаны режимы разгона и работы на холостом ходу, работы под нагрузкой, особенности работы в условиях перегрузки на валу турбины.

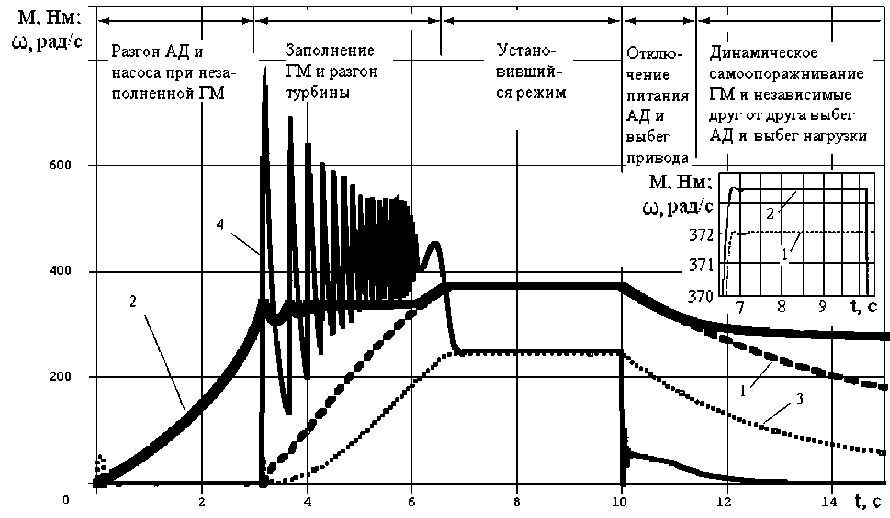
Рис. 5. Результаты компьютерного моделирования динамики привода при ГМ с динамическим самоопоражниванием

Для ГМ с динамическим самоопоражниванием результаты моделирования приведены на рис. 5, где график 1 — частота вращения турбины «турбины, график 2 — частота вращения насоса ГМ «насоса, график 3 — момент нагрузки на валу турбины Мнагружи, график 4 — момент на валу насоса ГМ Мнасосагм- Сценарий в этом случае следующий: пуск АД производится при незаполненном жидкостью рабочем объёме ГМ. Процесс заполнения ГМ рабочей жидкостью начинается при достижении валом насоса частоты вращения 90 % от номинальной, то есть при достижении «насосакр

(это начало разгона нагрузки и турбины). Привод выходит на устойчивый установившийся режим работы. В момент времени toff = 10 с происходит отключение питания АД. Вследствие этого при вод переходит в режим «выбега». При снижении частоты вращения вала насоса до 90 % от номинальной начинается процесс самоопоражнивания ГМ, по окончании которого ротор АД и нагрузка разъединяются, совершая далее «выбег» независимо друг от друга.

Выводы. Результаты компьютерного моделирования электрогидродинамического привода адекватно отражают сущность реальных физических процессов [12], происходящих на динамических и статических режимах асинхронного электропривода с ГМ. Использование ГМ с динамическим са-моопоражниванием позволяет осуществить присоединение нагрузки к уже разогнавшемуся АД, существенно облегчая процесс его пуска [12], рис. 5.