Компьютерное моделирование безоправочного волочения тонкостенных труб через вращаемую волоку

Тонкостенные трубы, изготавливаемые безоп-равочным волочением, обладают высоким качеством с точки зрения точности геометрических размеров, чистоты поверхности и механических свойств. Однако рост потребности в холоднотянутых трубах обуславливает необходимость совершенствования способов их производства.

В процессе безоправочного волочения значительная часть усилия уходит на преодоление внешнего трения трубной заготовки о рабочие стенки волоки. Уменьшить силы трения можно за счет приложения вращательного движения волоки в плоскости, перпендикулярной оси канала [1-4]. При таком движении контактная поверхность волоки перемещается относительно трубной заготовки по винтовой линии со скоростью в точке А V_рА (рис. 1), её составляющие:

V _окА = ω r _А = 2 π nr _А ,

F

к вА = в

FА ,

где ω – угловая скорость вращения волоки;

r_A – расстояние точки А от оси вращения;

n – число оборотов волоки в минуту;

V_в – скорость волочения;

V_окА – скорость перемещения в направлении вращения;

V_вА – скорость перемещения в направлении волочения;

F_А – площадь поперечного сечения трубы, проходящей через точку А ;

F_к – площадь поперечного сечения готовой трубы.

Ерисов Ярослав Александрович, студент.

Положение результирующего вектора скорости V_рА определяется углом

β = arctg ^{V окA}

^V вA .

В направлении, противоположном V_рА действует напряжение трения τ_А , проекции которого равны τ_А cos β и τ_А sin β . Значение τ_А определяется по закону Кулона:

τ _А = fp _А sin α , где f – коэффициент трения;

p_А – давление в канале волоки;

α – угол конуса рабочей зоны волоки.

При вращении волоки крутящим моментом М_в на контактной поверхности возникает реактивный момент трения М_тр , который передается трубе в очаге пластической деформации (ОПД). Таким образом, протягиваемая труба нагружается помимо усилия волочения P_в крутящим моментом, равным моменту от сил трения.

Рассматриваемый способ волочения при бе-зоправочном волочении мало изучен. В частности, нет данных о напряженно деформированном состоянии. Это затрудняет его использование на производстве.

В настоящей работе проведено компьютерное моделирование безоправочного волочения тонкостенных труб через вращаемую волоку с помощью метода конечных элементов (МКЭ) в специализированном программном комплексе ANSYS/LS-DYNA [5].

Для описания материала трубы принята модель упрочняющейся упруго-пластической среды – билинейная изотропная модель:

σi =σ0,2 + E′ei, где σi – напряжение течения;

σ _0,2 – предел текучести;

e _i – накопленная интенсивность деформаций;

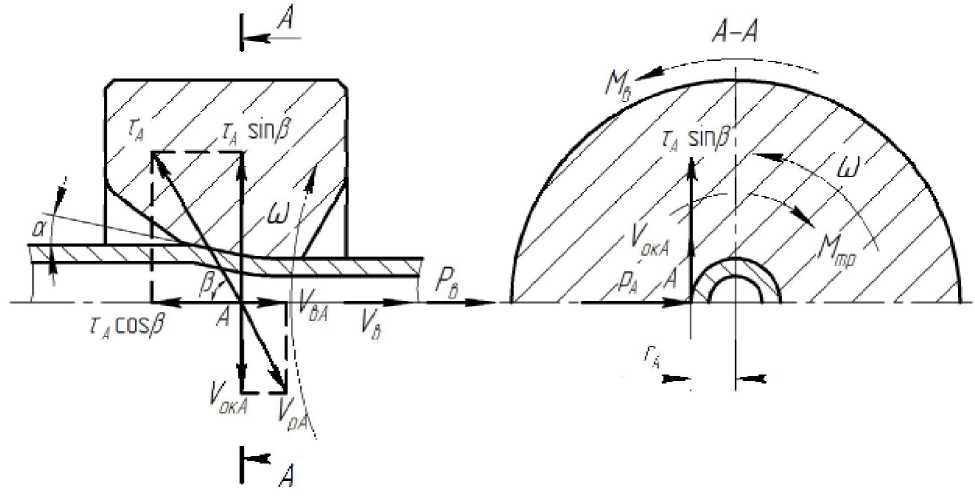
Рис. 1. Напряжения трения и скорости движения в канале вращающейся волоки

E ' - модуль упрочнения;

E,=       Ов - О0,2ln(1 + 5) + (^в - °0,2 )/E ,

О в - предел прочности;

5 — относительное удлинение;

E – модуль упругости.

Материал волоки сталь Х12МФ ( Е = 210 ГПа, n = 0,3) моделировали жестким.

Для построения трехмерной упорядоченной сетки конечных элементов выбрали оболочечные элементы. Конечно-элементная сетка трубы была сгенерированна с использованием 1920 элементов (длина ребра элемента 1 мм), волоки – 1936 элементов (0,5 мм) (рис. 2).

Компьютерное моделирование безоправоч-ного волочения тонкостенной трубы O10 мм из заготовки O13х1 мм из алюминиевого сплава Д16 (у0,2 = 320 МПа; ув = 450 МПа; Е = 72 ГПа; n = 0,34; д = 0,25) проводили в конические волоки с параметрами: угол конуса рабочей зоны – 12?; калибрующий поясок – 2,5 мм; радиус сопряже- ния обжимной и калибрующей зон – 5 мм. В расчетах принято f = 0,09; Vв = 15 м/мин; n = 1500 об/мин. Устойчивость процесса волочения обеспечивалась при длине трубы не менее 50 мм.

На установившейся стадии волочения через неподвижную и вращаемую волоку получено распределение компонент напряжений и деформаций в продольном сечении ОПД, показанное на рис. 3 и 4.

Из анализа графиков (рис. 3, а) следует, что осевые растягивающие напряжения o z , как следовало ожидать, возрастают к выходу из ОПД. Вращение волоки приводит к их снижению на 28%. Контактное давление p распределено в канале волоки неравномерно и имеет два экстремума на входе и выходе из ОПД. Причем пик давления на выходе из ОПД в 2,8 раза больше, чем на входе в ОПД. Величина тангенциальных напряжений ст_д по абсолютной величине при вращении волоки уменьшается, а р увеличивается.

Приложение вращательного движения к волоке приводит к увеличению радиальных дефор-

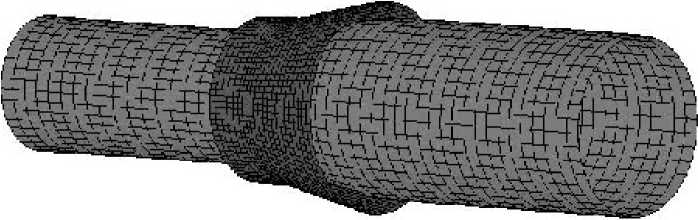
Рис. 2. Конечно-элементная сетка трубы и волоки

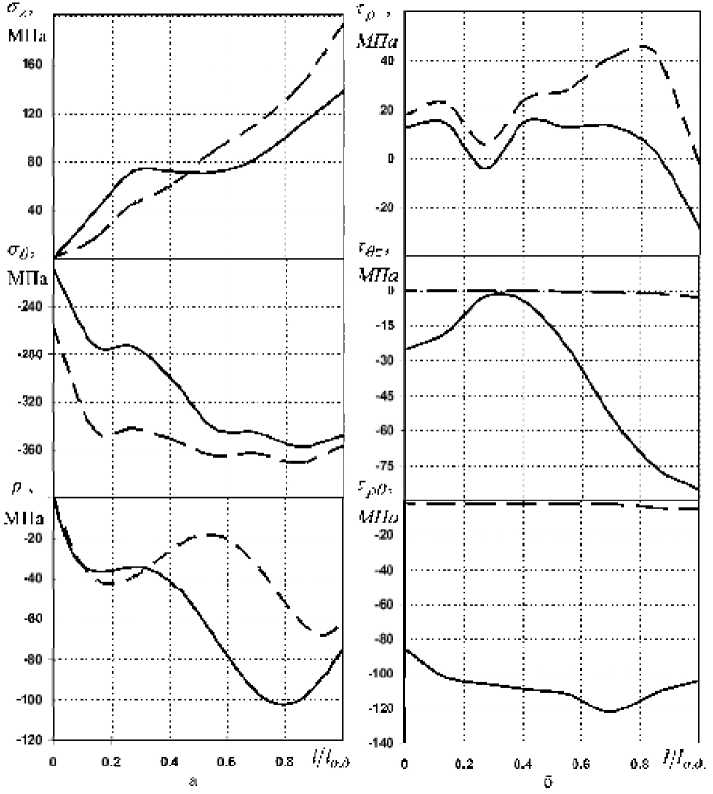
Рис. 3. Распределение компонент нормальных (а) и касательных (б) напряжений в продольном сечении ОПД:

---вращаемая волока; —--неподвижная волока

маций e_ρ на 20% (рис. 4, а), т.е. к более интенсивному утолщению стенки, что уменьшает длину протянутой трубы. При более высоких скоростях волочения с увеличением числа оборотов волоки толщина стенки растет менее интенсивно (рис. 5). Распределение тангенциальных e_θ и осевых e_z деформаций в продольном сечении ОПД вращаемой волоки отличается незначительно по сравнению с деформациями при волочении через неподвижную волоку.

В процессе волочения сдвиговые напряжения и деформации являются основным механизмом пластического формоизменения. Вращение волоки приводит к интенсификации сдвиговых напряжений и деформаций, что может оказать существенное влияние на формирование структуры и свойств готовых труб.

В поперечных сечениях ОПД по мере продвижения металла трубы вдоль канала вращаемой волоки касательные напряжения τθz и угловые деформации γθz приводят к осевому закручиванию трубы. Их величина нарастает от входа в ОПД, достигая своего максимального значения на выходе из ОПД. Установлено изменение схемы напряженного состояния с осесимметричной на объемную, что усложняет картину напряженно-деформированного состояния из-за наложения скручивающих сил и изменения условий на контактной поверхности “волока – заготовка”.

Получена зависимость усилия волочения P_в от числа оборотов волоки n при различных скоростях волочения V_в (рис. 5). При более высоких скоростях волочения для заметного снижения усилия необходимо вращать волоку с большим числом оборотов, что объясняется схемой сил, действующих в точке А контактной поверхности вращающейся волоки (рис. 1). Уменьшение сил трения, действующих в направлении, обратном волочению, тем значительнее, чем больше угол β .

Применение волочения через вращаемую волоку целесообразно при изготовлении тонкостенных труб большого диаметра, при моделировании которых установлено заметное уменьшение усилия с ростом числа оборотов волоки (рис. 5).

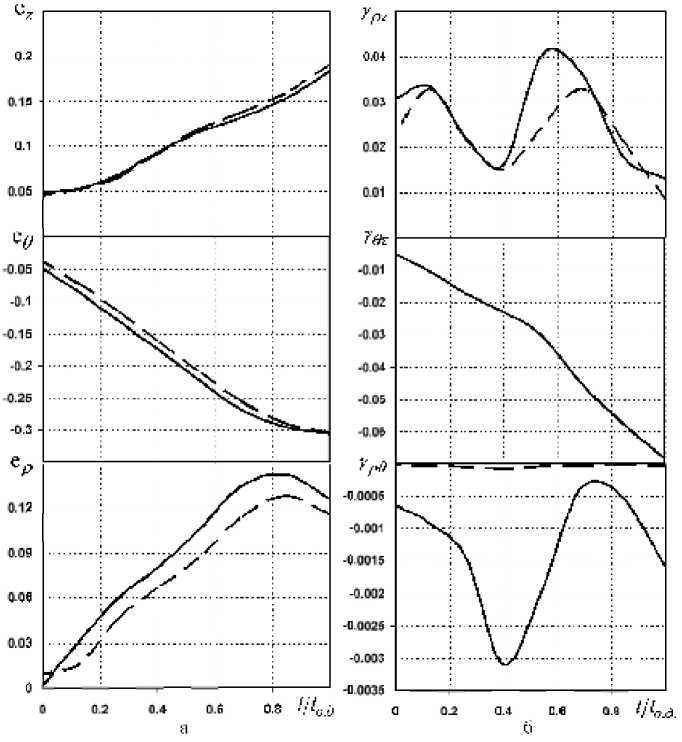
Рис. 4. Распределение линейных (а) и угловых (б) деформаций в продольном сечении ОПД: -----вращаемая волока; ---- – неподвижная волока

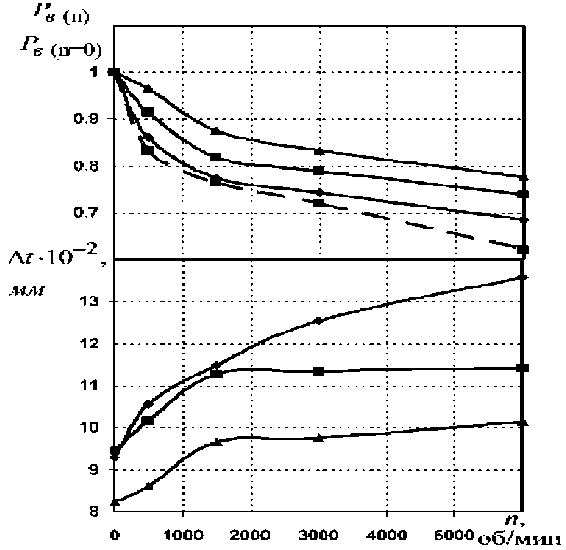
Рис. 5. Зависимость усилия волочения и толщины стенки от числа оборотов волоки:

~*— - V_B = 7,5 м/мин; ^е - V_B = 15 м/мин; ^ - V_B = 30 м/мин;

-- - D/t = 10; - - - D/t = 20

Таким образом, результаты компьютерного моделирования наглядно показывают особенности влияния кручения волоки в плоскости, перпендикулярной оси волочения, на изменение напряженно-деформированного состояния при безоправочном волочении тонкостенных труб.