Компьютерное моделирование динамики элемента сухого некулонова трения

движения, а также разработка достоверных методов идентификации динамических параметров механических систем с сухим некулоновым трением.

Для компьютерного моделирования динамики элемента с действующей силой сухого не-кулонова трения необходимо учитывать следующие факторы. Во-первых, необходимо выявить и задать так называемую «активную» обобщенную силу Q A как сумму всех действующих на систему сил, кроме сил сухого трения и сил инерции. Тогда уравнение движения тела массой m по обобщенной координате q можно представить в следующем виде:

q=-( Qa - Qtr )

m              .        (1)

В выражении (1) силу сухого некулонова трения Q TR зададим следующим образом:

9tnG?> —

/     ~F^'ec'™ 4 > °?

}      Рто,если. q < 0;

)-Ол,еыи4 = Он |А| -I Г„,еслж|(Ы >F„

где F_T D = F 0 — b 1 q + b 3 q & 3 - сила сухого некуло-нова трения движения; F TP – сила сухого трения покоя. При этом обычно F TP >F 0 .

Для построения и исследования математических моделей будем использовать среду визуального моделирования динамических систем Simulink/MATLAB [6]. Для численного решения уравнения (1) с учетом (2) создадим универсальный блок (рис. 1), входом которого будет являться текущее значение обобщенной активной силы Q A , а выходом – текущее значение обобщенной скорости q . Представленная блок-схема обеспечивает расчет обобщенной скорости

(выход 1 – «Skorost») динамической системы с сухим некулоновым трением при действии на неё некоторой внешней обобщенной активной силы (вход 1 – «QA»). Два дополнительных выхода рассмотренного блока подсистемы моделирования сухого некулонова трения позволяют исследовать изменения во времени ускорения (выход 2 – «Uskorenie») и самой силы сухого трения (выход 3 – «Fnec»).

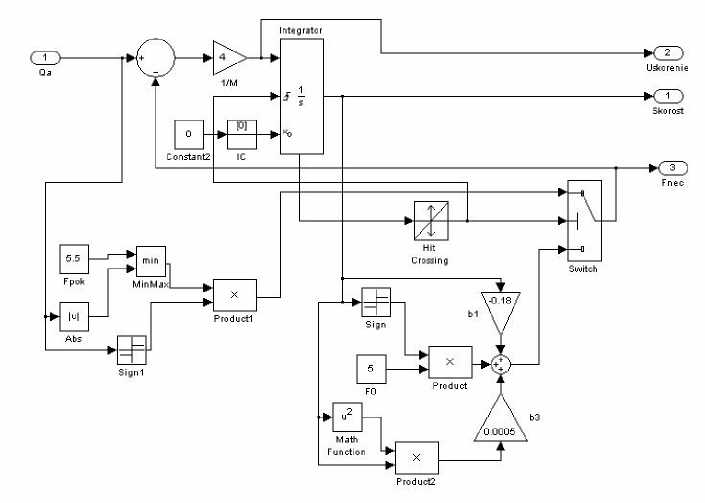
Рис. 1. Блок-схема подсистемы моделирования сухого некулонова трения

Рассмотрим теперь результаты компьютерного математического моделирования динамического поведения простейшей системы с сухим некулоновым трением, расчетная схема которой представлена на рис. 2, находящейся под воздействием внешней гармонической силы Psin ( ωt + φ ).

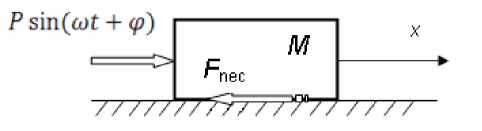
Рис. 2. Расчетная схема простейшей динамической системы с сухим некулоновым трением

Дифференциальное уравнение, описывающее поведение рассматриваемой системы, имеет следующий вид:

Mx + Fnec (x) = P sin (го • t + ф)

где M – приведенная масса системы; F_nec ( x & ) – значение некулоновой силы сухого трения, определяемой согласно выражению (2); P, ω, φ – соответственно амплитуда, частота и начальная фаза вынуждающей гармонической силы.

На рис. 3 представлена блок-схема Simulink-модели для численного интегрирования уравнения (3) установленным методом ode 23 (Bogacki-Shampine) с переменным шагом и относительной точностью 10^-5.

На рис. 4 показаны графики изменения во времени отдельных динамических характеристик рассматриваемой системы, синхронизированные во времени. Это позволяет эффективнее проанализировать характер их поведения и взаимозависимость. Например, из анализа представленных графиков отчетливо видно, что скольжение груза начинается при превышении вынуждающей силой силы трения покоя F pok =5,5 Н. Остановка системы происходит, когда сила трения и вынуждающая силы уравновесятся силами инерции. Движение системы в данном случае реализуется с продолжительными остановками. Сила трения во время этих остановок (схватывания с опорной поверхностью) «копирует» вынуждающую гармоническую силу, что хорошо согласуется с известными физическими представлениями.

Закон изменения самой силы сухого трения во времени имеет сложный характер, обусловленный прерывистостью движения, изменением направления движения и зависимостью значения силы некулонова трения от значения скорости скольжения. Реализуемый закон силы сухого некулонова трения в функции скорости скольжения представлен на рис. 5. Петля гистерезиса, площадь которой соответствует рассеиваемой силами трения механической энергии за один период движения системы, представлена на рис. 6.

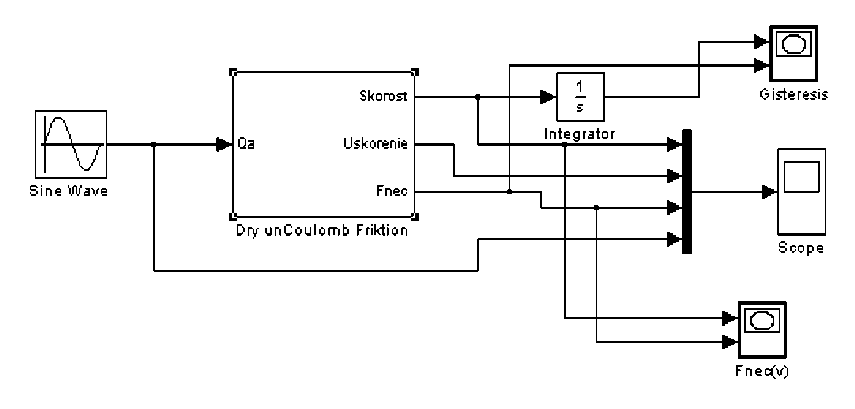
Рис. 3. Блок-схема Simulink-модели простейшей динамической системы с сухим некулоновым трением

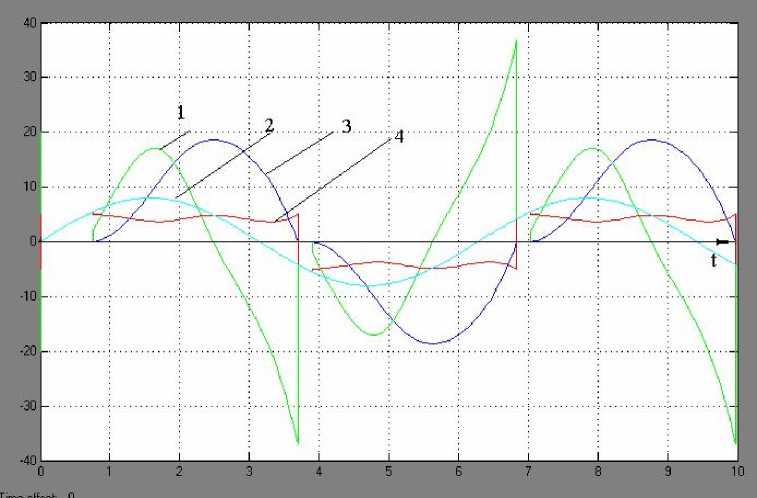
Рис. 4. Законы изменения во времени динамических характеристик исследуемой системы: 1 – ускорение, 2 – вынуждающая гармоническая сила, 3 – скорость, 4 – сила сухого некулонова трения

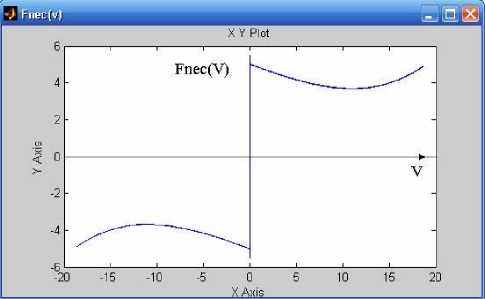
Рис. 5. Закон изменения силы сухого некулоно-ва трения от скорости скольжения ( F poc =5,5 (Н); F 0 =5 (Н); b 1 =0,18 Hc/м, b 3 =0,005 Нс³/м³)

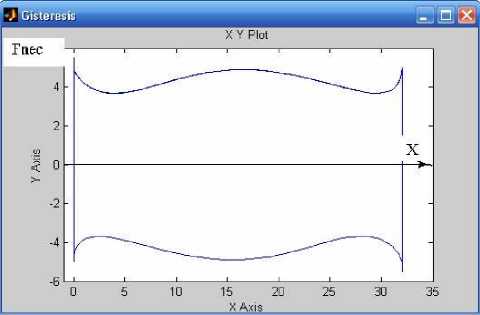
Рис. 6. Петля гистерезиса системы с некулоновым трением

Для проверки адекватности функционирования разработанного комплекса по моделированию динамических процессов в системах с сухим некулоновым трением рассмотрим классическую задачу возникновения фрикционных автоколебаний в такой системе, причиной которых как раз и является наличие падающего участка на законе F_nec ( x ^& ) . Расчетная схема исследуемой динамической системы представлена на рис. 7. Дифференциальное уравнение динамики данной системы имеет вид:

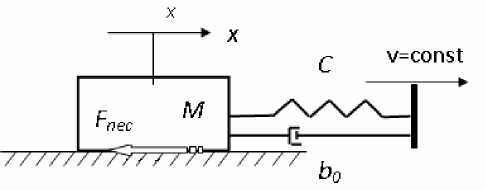
Рис. 7. Расчетная динамическая схема системы для исследования фрикционных автоколебаний

Mx + Fnec (x) + C (x - vt) + b 0( x^ - v) = 0, (4)

где C – коэффициент жесткости упругого элемента; b 0 – коэффициент вязкого сопротивления; v=const – постоянная скорость перемещения правого конца упругого элемента; ^{F nec ( x & )} – закон изменения силы сухого некулонова трения с падающей характеристикой от скорости в соответствии с принятой моделью (2).

Блок-схема Simulink-модели для численного решения уравнения (4) представлена на рис. 8. При исследовании приняты следующие значения параметров математической модели (4): M =0.25(кг); С =2(Н/м); b 0 =0.12 (Нс/м); v =4(м/с); F poc =F 0 =5 (Н); b 1 =0,18 Hc/м, b 3 =0,005 Нс³/м³.

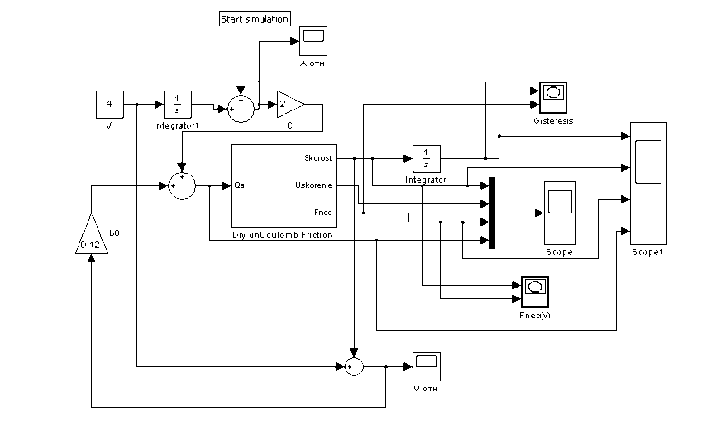
Рис. 8. Блок-схема Simulink-модели для исследования фрикционных автоколебаний

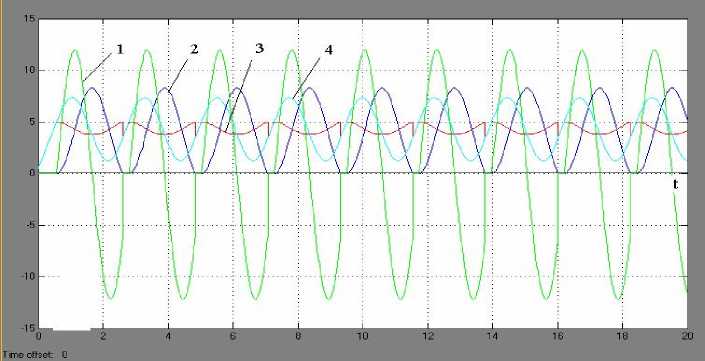
Рис. 9. Результаты моделирования фрикционных автоколебаний (копия экрана «Scope»): 1 – ускорение; 2 – скорость; 3 – сила сухого некулонова трения; 4–упругая сила пружины

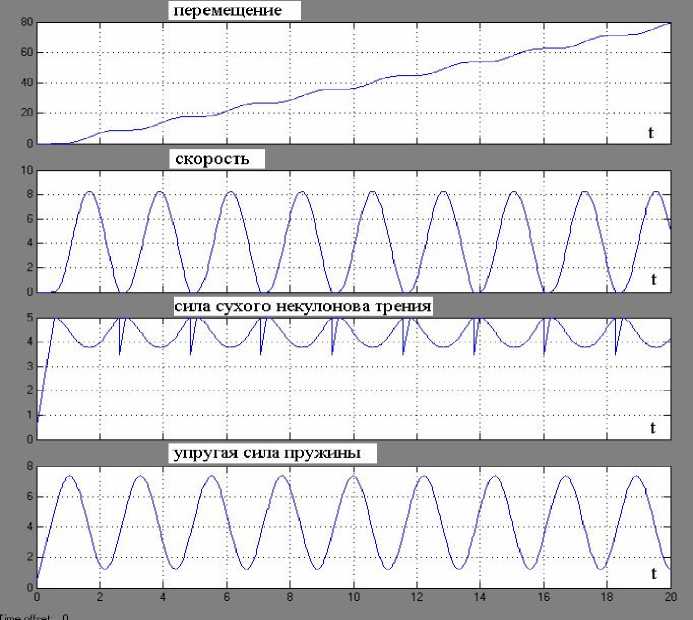
Рис. 10. Результаты моделирования фрикционных автоколебаний (копия экрана «Scope 1»)

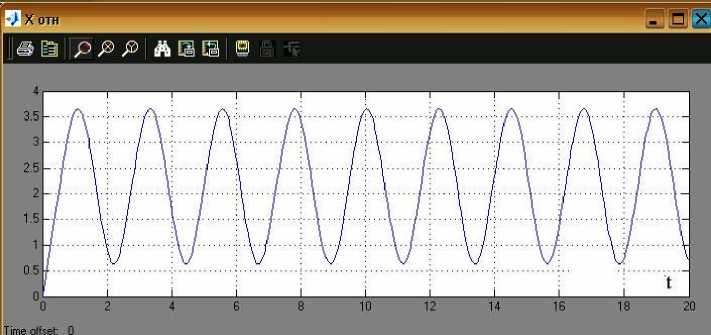
Рис. 11. График изменения относительного перемещения груза и правого конца упругого элемента

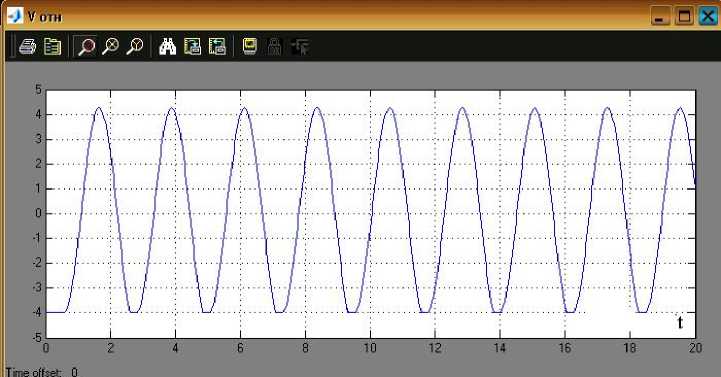
Рис. 12. График изменения относительной скорости груза и правого конца упругого элемента

На рис. 9 и 10 представлены результаты моделирования рассматриваемой системы в среде Simulink/MatLAB. Из анализа приведенных графиков видно, что груз М совершает квази-гармонические фрикционные автоколебания с частотой f =0,44 Гц, сопровождаемые периодическими остановками продолжительностью t ост =0,2 с. Амплитудные значения скорости груза превышают 8 м/с. Сила сухого некулонова трения имеет сложный закон изменения во времени, обусловленный падающим участком и прерывистым характером движения с остановками. На рис. 11 и 12 показаны графики относительного смещения и относительной скорости груза и правого конца упругого элемента, перемещаемого с постоянной скоростью. При этом хорошо заметны остановки груза, а также квази-гармонический характер движения.

Таким образом, известный характер поведения рассматриваемой системы полностью подтвердился при компьютерном вычислительном эксперименте.

Выводы: рассмотренная компьютерная модель сухого некулонова трения, представленная средствами блочного имитационного моделирования Simulink/MatLab, позволяет адекватно описывать динамические процессы, в частности, фрикционные автоколебания. Особо важным и сложным при моделировании является обеспечение соответствующего характера изменения силы сухого некулонова трения на этапах скольжения и относительного покоя поверхностей трения, а также определение момента смены одного этапа другим.

Работа выполнена в рамках реализации Федеральной целевой программы «Научные и научнопедагогические кадры инновационной России» на 2009-2013 годы по проблеме «Исследование закономерностей движения и идентификация динамических параметров механических систем с сухим неку-лоновым трением» (гос. регистр. № П2243, шифр НК 422П).