Компьютерное моделирование газонаполненных сепараторов. I. Конфигурирование ионно-оптической схемы

Газонаполненные сепараторы широко используются в ядерной физике для исследования структуры продуктов деления тяжелых ядер и для выделения сверхтяжелых элементов в асимметричных реакциях синтеза при бомбардировке твердых мишеней быстрыми частицами — нейтроноизбыточными изотопами [1]. Последняя задача привлекает в настоящее время наибольшее внимание в связи с недавними удачными экспериментами по синтезу новых элементов с атомными номерами 114 и 116 и попытками синтеза последующих элементов, приближающими к гипотетическому "острову стабильности" сверхтяжелых элементов [2]. Эти эксперименты проводятся сейчас в исследовательских центрах Дубны [3, 4], Berkeley [5], Jy-väskylä (Finland) [6, 7], Osaka [8, 9], Darmstadt [10]. Газонаполненные сепараторы этих научных центров включают в себя: дипольный магнит (D) с однородным полем, осуществляющий сепарацию частиц, и ряд квадрупольных магнитных линз (Q), (чаще в виде дублета), фокусирующих пучок на детектор. Возможности такой схемы, как было отмечено в недавнем обзоре [1], представляются исчерпанными, и для развития исследований в этой области необходимы инструменты с улучшенными характеристиками.

Разработка новых сложных исследовательских систем, какими являются газонаполненные сепараторы, требует большого объема математического моделирования и исследований на базе оптики заряженных частиц с учетом взаимодействия с газовой средой. Последнее обстоятельство является весьма существенным, поскольку ионно-оптические характеристики газонаполненных сепараторов в очень большой степени определяются этим взаимодействием.

Разработанные к настоящему времени компьютерные модели газонаполненных сепараторов как у нас в стране [11], так и за рубежом [10, 12–14] привязаны к конкретным ионно-оптическим схемам и в основном ориентированы на калибровку сепараторов. Разработанные модели движения заряженных частиц не в полной мере учитывают физические процессы, в частности не учитываются многоэлектронные процессы обмена зарядом. До сих пор не было проведено систематического сравнения различных схем, не исследовались схемы, отличные от классической схемы DQQ и включающие в себя различные комбинации дипольных магнитов, в том числе с неоднородным полем, и квадрупольных линз.

Целью данной работы является разработка компьютерной модели газонаполненного сепаратора произвольной конфигурации, ионно-оптическая схема которого включает произвольное число дипольных магнитов и квадрупольных линз, разделенных бесполевыми промежутками и расположенных в произвольном порядке. В качестве основного метода решения задачи исследования ионно-оптических характеристик принят траекторный анализ, основанный на методе статистического моделирования, позволяющий в полной мере учитывать физические, технологические и конструктивные параметры моделируемой установки. Основное внимание в этой работе уделено методам конфигурирования ионно-оптической схемы.

ПРИНЦИП ДЕЙСТВИЯ

ГАЗОНАПОЛНЕННОГО СЕПАРАТОРА

Принцип работы газонаполненного сепаратора описан в ряде работ (см., например, [5, 10–12, 15]). Диспергирующим элементом сепаратора является дипольный магнит. Ион массы m , имеющий заряд q и скорость v , в магнитном поле индукции B в вакууме движется по траектории, определяемой силой Лоренца

F = q[ v x B ].                      (1)

Магнитная жесткость иона

B p = mv ,                    (2)

q где p — радиус кривизны траектории (предполагается B±v), определяет траекторию его движения в однородном поле дипольного магнита. Ионы данной массы с различной магнитной жесткостью движутся по различным траекториям. Их распределение в фокальной плоскости сильно зависит от начальных распределений по скоростям и зарядам.

Если область магнитного поля заполнена газом, траектория движения иона наряду с магнитным полем определяется также столкновениями с молекулами газа. При столкновениях изменяется скорость иона (как по величине, так и по направлению) и его заряд. Если число столкновений достаточно велико, траектории ионов концентрируются вблизи траектории, соответствующей значению магнит ной ж есткости, определяемой средней величиной ( v / q ), где q — средний равновесный заряд иона, устанавливающийся в результате большого числа взаимодействий с молекулами среды с передачей одного или нескольких электронов.

Если принять приближение Бора для среднего заряда v 1/3

q = —Z ,                  (3)

v ₀

где Z — атомный номер иона, v 0 = e ² / h = = 2.19 • 10 8 см/с — боровская скорость, то для магнитной жесткости получаем

B p =    = 0.⁰²²⁶⁷ ^(T • м),     (4)

где A — масса иона в атомных единицах m ₀ ( m = Am 0 ).

В этом приближении радиус кривизны траектории иона в магнитном поле зависит только от его массы и атомного номера (заряда ядра) и не зависит от ионного заряда и скорости. На этом основан принцип действия газонаполненного сепаратора: все ионы данной массы независимо от их начального заряда и скорости будут собраны в ограниченной области фокальной плоскости.

Размеры фокального пятна определяются главным образом характером флуктуаций ионного заряда, угловым рассеянием из-за многократных столкновений с молекулами газа и размерами области источника ионов (области зарождения продуктов ядерных реакций). Определенный вклад вносит разброс ионов по скоростям и скоростная зависимость среднего заряда, в принципе отличная от боровской (3). Перечисленные выше составляющие вклада в размеры фокального пятна неустранимы в силу самого принципа действия газонаполненного сепаратора, их вклад значительно выше вклада ионно-оптических аберраций. Поэтому газонаполненные сепараторы отличаются невысокой разрешающей способностью по массам и уступают по этому параметру вакуумным сепараторам. Однако независимость их аксептанса от начального ионного заряда и скорости крайне важна при выделении продуктов ядерных реакций, имеющих очень широкие распределения по скоростям и ионным зарядам. Газонаполненные сепараторы остаются незаменимыми в тех задачах, где требуется высокое пропускание и где их основной недостаток — невысокая разрешающая способность — не играет большой роли [1].

ПОСТРОЕНИЕ ИОННО-ОПТИЧЕСКОЙ СХЕМЫ СЕПАРАТОРА

В газонаполненных сепараторах используются только элементы с магнитным полем: дипольные (D) и квадрупольные (Q) магниты. Любую схему сепаратора можно представить в виде определенной комбинации этих двух элементов, разделенных бесполевыми промежутками и диафрагмами. Таким образом, основными блоками, позволяющими построить ионно-оптическую схему (ИОС) произвольного сепаратора, являются:

α — дипольный магнит D;

β — квадрупольный магнит Qh или Qv (индексы h или v показывают соответственно фокусировку в горизонтальной или вертикальной плоскости);

γ — бесполевой промежуток или бесполевой канал (диафрагма).

Дипольный магнит описывается следующими ионно-оптическими и геометрическими параметрами:

• а)    углом поворота и радиусом центральной траектории ф и p ; при этом условимся, что Ф >  0, p >  0, если поворот происходит по часовой стрелке, в противном случае ф <  0, p <  0 . При таком выборе знаков длина центральной траектории в магнитном поле S D = pф положительна.

• б)    углами наклона входной и выходной границ

магнитного поля ε и ε ; положительные значения этих углов отвечают фокусировке в вертикальной плоскости.

• в)    углом λ полураствора полюсных наконечников конусных полюсов магнита.

• г)    величиной G полузазора полюсных наконечников магнита.

Квадрупольный магнит описывается длиной центральной траектории в магнитном поле S _Q , радиусом апертуры r _a и значением индукции магнитного поля B вблизи полюсов.

Бесполевой промежуток и бесполевой канал (диафрагма) описываются их геометрическими размерами: длиной и размерами поперечного сечения.

Каркасом, на котором строится схема сепаратора, является центральная (осевая) траектория, состоящая для рассматриваемых нами элементов из отрезков прямых (для элементов типа β или γ ) и дуг окружности (для элементов типа α ). Для ее описания вводится глобальная система координат (ГСК) XYZ. Будем считать, что плоскость XY — плоскость дисперсии (плоскость симметрии дипольных магнитов), или горизонтальная плоскость, XZ — вертикальная плоскость (рис. 1). Каждому из элементов соотнесем свою двумерную локальную систему координат (ЛСК) xi yi в плоскости XY , где i — порядковый номер элемента в схеме (рис. 1). Начало координат O i локальной системы координат i-го элемента поместим в точку входа центральной траектории в этот элемент, а ось O i xi направим вдоль центральной траектории. Локальная система координат полностью определяется глобальными координатами ее начала XОiYОi и углом Ψi между осью O i xi и осью OX, который назовем углом ориентации ЛСК. Будем считать Ψi > 0, если поворот от оси OX к оси O i xi осуществляется по часовой стрелке, и Ψi< 0, если — против.

Для элемента с поворотом центральной траектории (типа α ) при ρ _i <  0 осуществляем дополнительно отражение относительно оси O ⁱ xⁱ , так что ось O ⁱ yⁱ будет направлена вдоль радиуса центральной траектории в точке входа по направлению от центра кривизны. Такое преобразование обеспечит нам инвариантность выражений для траекторий движения иона в ЛСК как при ρ _i >  0 , так и при ρ _i <  0 .

Координаты начала ЛСК ( i+ 1)-го элемента в глобальной системе координат и угол поворота Ψ_i полностью определяются рекуррентными соотношениями.

Если i -й элемент — элемент с прямолинейной центральной траекторией (элемент типа β или γ ), то для глобальных координат начала ЛСК ( i+ 1)-го элемента имеем (см. рис. 2)

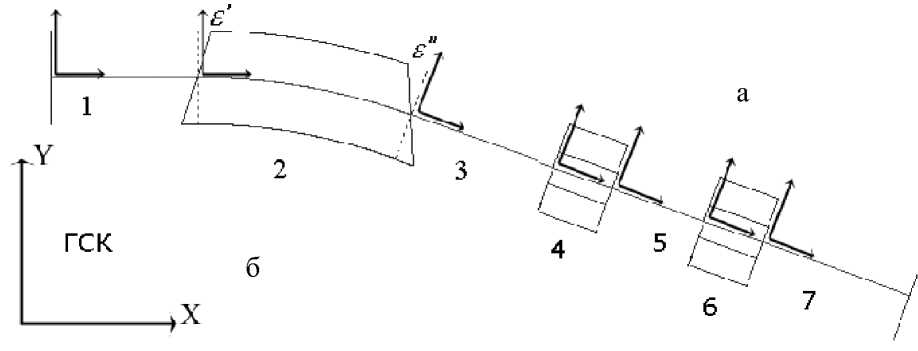
Рис. 1. Сепаратор из семи элементов.

а — совокупность локальных систем координат (ЛСК);

б — глобальная система координат (ГСК)

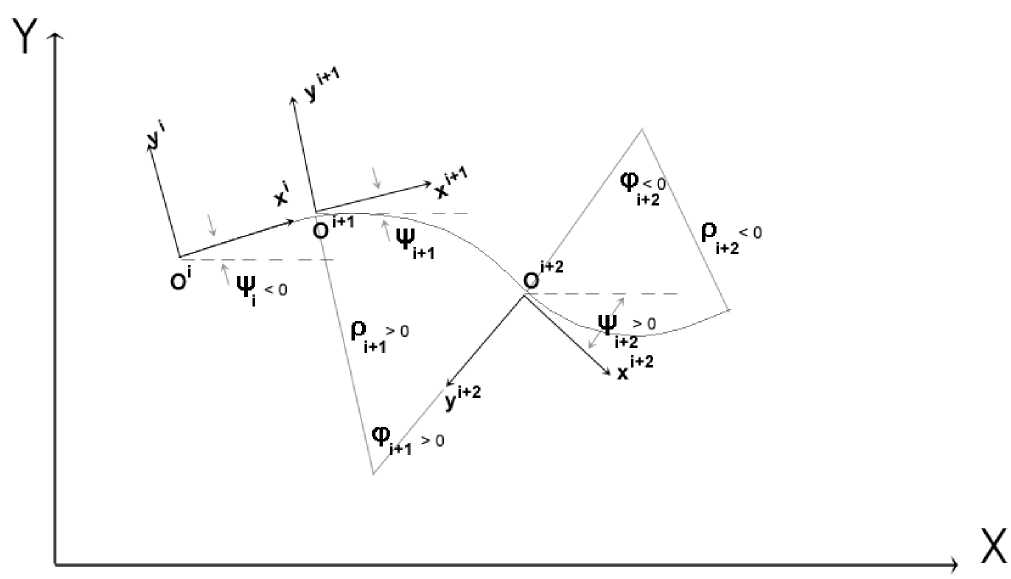
Рис. 2. Локальные системы координат для трех последовательных элементов схемы: c прямолинейной осевой траекторией (i-й элемент), c поворотом центральной траектории по часовой стрелке ((i+1)-й элемент), c поворотом центральной траектории против часовой стрелки ((i+2)-й элемент)

X Oi + 1 = X Oi + S i cos ^ i ,

’^i = Y oi — S i -sin ^ i ,                  (5)

. УМ = ^i, где Si — длина центральной траектории в i-м элементе.

Если i -й элемент — элемент типа α с поворотом центральной траектории, то

X Oi + 1 = X Oi ⁺ P i (sin ^ i + 1 - sin ^ i ),

• - O oi + 1 = O oi + P i (cos ^ + i - cos ^ i ),             (6)

. ^ i + i = ^ i + V i -

Единообразие соотношений (6) обеспечивается указанным выше выбором знаков параметров ф и р .

Конфигурация системы сепаратора — число, последовательность и тип элементов схемы и их параметры — однозначно определяет множество локальных систем координат: координаты начала ЛСК и их ориентацию.

Если известны координаты точки траектории

( x , y , z ) в локальной системе координат i -го элемента, то ее координаты в глобальной системе определятся с учетом поворота вокруг оси O ⁱ zⁱ на угол Ψ i и параллельного переноса начала координат:

X = X oi + x cos ^ i + y sin ^ i ,

• - У = Yoi ^- x sin Ф i + y cos Ф i , (7) Z = z .

Для элементов типа α (с поворотом центральной траектории) при p i <  0 сначала проводим отражение относительно оси O i X : y ^ - y , а затем определяем глобальные координаты по формулам (7).

Тем самым мы описали траекторию иона как в локальной, так и в глобальной системе координат, связанной с установкой в целом. При этом локальные системы координат обеспечивают нам возможность записывать уравнения траекторий в инвариантном виде.

Начальными значениями для уравнений траектории в (i+1)-м элементе являются координаты конечных точек траекторий в i-м элементе, пере- считанные в ЛСК (i+1)-го элемента, в том числе с учетом отражения, если (i+1)-й элемент типа α с Pi+1 < 0.

Введение локальных систем координат для каждого элемента схемы позволяет достаточно просто проверять геометрические условия прохождения с учетом величины межполюсного зазора дипольных магнитов, радиуса апертуры квадрупольных линз и размеров диафрагм.

Таким образом, произвольная конфигурация сепаратора может быть описана в глобальной системе координат с помощью совокупности ЛСК в плоскости Z = 0, связанных с ней преобразованиями параллельного переноса, поворота и отражения относительно оси.

МОДЕЛИРОВАНИЕ ТРАЕКТОРИЙ

Для описания траекторий используется стандартная техника статистического моделирования. В ее основу положена микроскопическая модель движения ионов в газовой среде [16], учитывающая процессы обмена электронами иона с молекулами газа, рассеяние ионов на малые углы в результате многократных столкновений и потери энергии. В качестве промежутка дискретизации траектории принимается случайная величина — длина свободного пробега l между двумя последовательными столкновениями с изменением заряда иона. Длина свободного пробега генерируется в соответствии с соотношением l = -X In R,

где R — равномерно распределенное на промежутке [0, 1) случа й ное число. Средняя длина свободного пробега X определяется полным сечением ст tot процесса изменения заряда и концентрацией n молекул газа

X = 1/( п ст tot ). (9)

В каждой точке столкновения производится изменение заряда иона в соответствии с вероятностями захвата ст cl ст _tot и потери электрона ст _l / ст _tot. В этих формулах ст c и ст _l — сечения захвата и потери электрона соответственно, ^ст c ^{+ ст} i = ^ст tot -

В этой же точке производится пересчет направления движения и энергии частицы. В соответствии с принятой моделью угол отклонения траектории иона разыгрывается по нормальному закону

Р ( 6 ) =

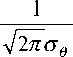
( exp

V

62 '

2 ст _е ²

6 7

.

Стандартное отклонение распределения ст₆ пропорционально длине l отрезка траектории, пройденной ионом до столкновения, и концентрации молекул газа n . Его численное значение определяется на основе формализма Мейера [17], Зигмунда [18].

Энергия частицы уменьшается на величину

^ E = sl ,                         (11)

где s = - d E /d x — коэффициент торможения, значения для которого берутся из таблиц [19]. Скоростная зависимость коэффициента торможения определяется в соответствии с формулой Линдхар-да—Шарфа [20], если скорость иона сравнима со скоростями атомных электронов, но не слишком велика ( v <  Z ^2/3 v ₀ , Z — атомный номер иона),

S = C Ls n- ,                   (12)

v ₀

или в соответствии с формулой Бете—Блоха [21] для больших значений скорости v2

s = C BB n —0- ln(2 mv ² l I ),             (13)

v ²

где I — средний потенциал возбуждения атомов среды. Коэффициенты C_LS и C_BB определяются атомными номерами иона и атомов среды [21].

На длине свободного пробега l ион движется по траектории, определяемой только внешним магнитным полем. Выражения для этих траекторий могут быть взяты в параксиальном приближении, поскольку вклад ионно-оптических аберраций в размеры фокального пятна значительно меньше вклада, обусловленного взаимодействием с молекулами среды.

ОПИСАНИЕ ПРОГРАММЫ

Общая схема моделирования представлена на рис. 3.

Ионно-оптическая схема сепаратора представляется в программе в терминах блоков. Каждый блок — это элемент схемы со своими параметрами и соответствующая ему процедура расчета. Например, для элемента схемы "магнитный диполь" будем иметь:

• •    блок — дипольный магнит;

• •    расчетная процедура — dmgnGFS;

• •    параметры: углы наклона входной и выходной границ; длина и радиус центральной траектории в элементе; угол полураствора и величина полузазора полюсных наконечников конусных полюсов магнита.

  

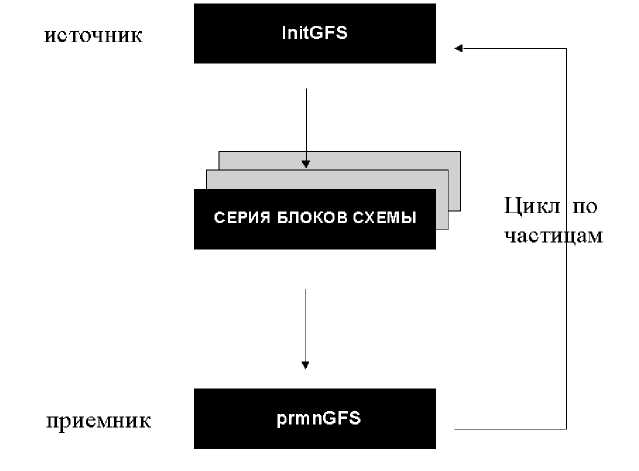
  Рис. 3. Общая схема программы

  
  

  Перечень типовых элементов и соответствующих расчетных процедур программы

  Типовой элемент	Расчетная процедура
  Бесполевой промежуток	poletGFS
  Бесполевой канал (диафрагма)	trandGFS
  Вход в дипольный магнит	entmGFS
  Дипольный магнит	dmgnGFS
  Выход из дипольного магнита	eximGFS
  Квадрупольный магнит	qmgnGFS
  Приемник	prmnGFS

  
  

Перечень типовых элементов (блоков) и соответствующих им расчетных процедур приведен в таблице. Любая ионно-оптическая схема может быть задана последовательностью таких блоков. Расчетные процедуры блоков "Бесполевой промежуток", "Бесполевой канал", "Вход в дипольный магнит", "Выход из дипольного магнита", "Приемник" моделируют движение ионов в бесполевом пространстве элементов схемы различной геомет- рической конфигурации. Блоки "Вход в дипольный магнит" и "Выход из дипольного магнита" выделены в отдельные группы для удобства моделирования схем с косыми углами входной и выходной границ магнитного поля дипольного магнита. Расчетные процедуры блоков "Дипольный магнит" и "Квадрупольный магнит" моделируют движение ионов в однородном и квадрупольном магнитных полях соответственно.

Все начальные параметры программы хранятся в текстовом файле, который считывается при каждом запуске программы. В текстовом файле хранятся несколько групп данных, каждая из которых отвечает за определенную часть работы программы. Среди этих групп:

• 1)    параметры окон (при запуске программы в качестве Windows ^TM -приложения );

• 2)    параметры схемы и геометрии;

• 3)    полевые параметры магнитных элементов;

• 4)    параметры начальных условий движения;

• 5)    параметры блока рассеяния;

• 6)    параметры режима счета и вывода результатов.

Параметры второй и третьей групп задаются в виде массивов, среди которых имеется массив конфигурации, определяющий порядок и тип элементов схемы. Такой подход позволяет в рамках единого кода сконфигурировать любую схему.

Расчет траекторий начинается с вызова процедуры initGFS (рис. 3), в которой генерируются начальные условия движения. Далее для каждой траектории производится последовательный проход по элементам схемы. Данные, полученные в результате работы программы, хранятся в виде одномерных и двумерных гистограмм распределений частиц по координатам, энергиям и зарядам.

Программа позволяет проводить моделирование траекторий без учета взаимодействия ионов со средой, а также с включением лишь отдельных факторов этого взаимодействия: малоуглового рассеяния, потери энергии, изменения заряда. Это позволяет исследовать вклад каждого из перечисленных факторов в отдельности.

Программа предусматривает два режима работы: фоновый и стандартный. При стандартном запуске программа работает как многооконное Windows ^TM -приложение для одного набора начальных параметров. В этом режиме визуализируются схема и траектории ионов как в горизонтальной, так и в вертикальной плоскостях. При запуске в фоновом режиме программа запускается без визуального вывода на длительное время, как правило, с несколькими наборами начальных параметров. Фоновый режим позволяет более эффективно использовать программу, запуская ее с целым набором файлов начальных данных, а также позволяет делать выборку по значениям одного или нескольких параметров для каждого файла.

На рис. 4–8 представлены примеры конфигурирования ряда схем реально существующих и гипотетических сепараторов.

Газонаполненный сепаратор DGFRS Лаборатории ядерных реакций ОИЯИ (г. Дубна) имеет конфигурацию DQhQv [11]: дипольный магнит с однородным полем—квадрупольный магнит с фокусировкой в горизонтальной плоскости— квадрупольный магнит с фокусировкой в вертикальной плоскости. Горизонтальный разрез его ионно-оптической схемы приведен на рис. 4. Здесь же показаны параксиальные траектории ионов без учета взаимодействия со средой. На рис. 5 приведены горизонтальный и вертикальный разрезы той же схемы со спрямленной центральной траекторией и с базовыми параксиальными траекториями.

Аналогичную конфигурацию имеют сепараторы SASSY [5], HECK [10], проектируемая модификация сепаратора RITU [7].

Принципиально иную конфигурацию имеет сепаратор JOSEF [22]. Он имеет симметричную схему и состоит из трех последовательно расположенных дипольных магнитов, причем первый и последний — с однородным полем, средний магнит — с полем B ~ 1/ ρ (рис. 6, 7).

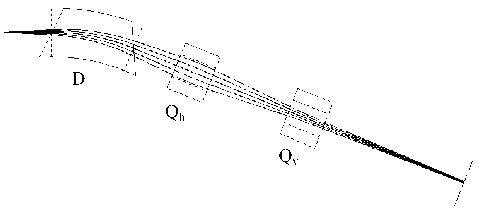
Рис. 4. Ионно-оптическая схема газонаполненного сепаратора Лаборатории ядерных реакций ОИЯИ (г. Дубна) [11]. Конфигурация DQ_hQ_v . Приведены параксиальные траектории ионов без учета взаимодействия

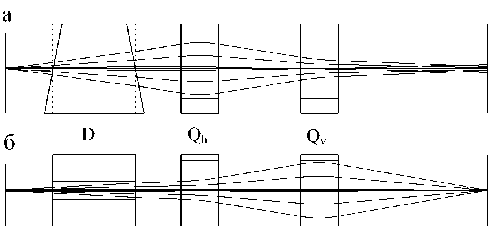
Рис. 5. Горизонтальный со спрямленной осевой траекторией (а) и вертикальный (б) разрезы схемы газонаполненного сепаратора Лаборатории ядер-ных реакций ОИЯИ (г. Дубна)

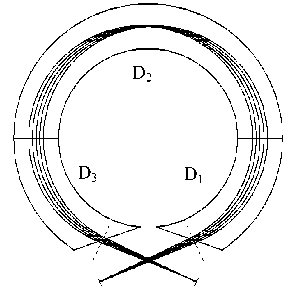
Рис. 6. Ионно-оптическая схема сепаратора JOSEF [22]. Конфигурация DDD

На рис. 8 приведены две гипотетические схемы, состоящие из одинаковых элементов: двух дипольных и одного квадрупольного магнита. В первой схеме поворот центральной траектории в дипольных магнитах осуществляется в одном направлении ("С-конфигурация"), во второй — в противоположных ("S-конфигурация"). Сравнение этих схем по степени уширения пучка ионов представляет интерес в связи с установленными ранее свойствами тандемных изотопных масс-спектрометров по изотопической чувствительности [23]: рассеяние ионов на остаточном газе вносит меньший вклад в уширение пиков в масс-спектрометрах, построенных по схеме S, по сравнению со схемой C.

Результатам моделирования траекторий ионов с учетом всего многообразия процессов рассеяния и сравнению различных схем будет посвящена отдельная статья.

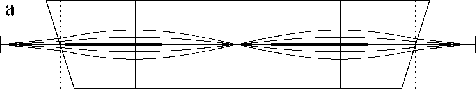
б          D 1              D₂              D 3

ВЫВОДЫ

Рис. 7. Горизонтальный со спрямленной осевой траекторией (а) и вертикальный (б) разрезы схемы сепаратора JOSEF

Предложенная методика и разработанные на ее основе алгоритм и программа конфигурирования ионно-оптической схемы составляют основу компьютерной модели газонаполненного сепаратора и позволяют генерировать схему, состоящую из произвольного числа элементов: дипольных магнитов, квадрупольных линз, диафрагм и бесполе-вых промежутков. Число элементов ограничено только ресурсами компьютера.

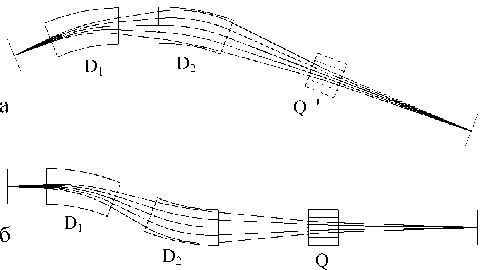
Рис. 8. Ионно-оптические схемы DDQ-сепараторов: а — "С-конфигурации" (поворот центральной траектории в дипольных магнитах осуществляется в одном направлении) и б — "S-конфигурации" (поворот центральной траектории в дипольных магнитах осуществляется в противоположных направлениях)

Введенные в работе глобальная система координат и связанные с отдельными элементами схемы локальные системы координат, получающиеся в результате параллельного переноса, поворота и отражения относительно оси, позволяют записывать уравнения траекторий ионов в различных элементах в инвариантном виде.