Компьютерное моделирование газонаполненных сепараторов. II. Флуктуации ионного заряда

Настоящая работа, являющаяся продолжением работы [1], посвящена построению математической модели флуктуации ионного заряда при движении быстрой заряженной атомной частицы в газовой среде ионно-оптических трактов газонаполненных сепараторов.

Флуктуации заряда наряду с угловым рассеянием ионов при многократных столкновениях с молекулами газа вносят основной вклад в уширение ионного пучка. В основном этими факторами определяется разрешение газонаполненного сепаратора [2]. Определенный, но существенно меньший вклад в размеры фокального пятна вносит разброс ионов по скоростям и скоростная зависимость среднего равновесного заряда. Все эти факторы неустранимы в силу самого принципа действия газонаполненного сепаратора. Поэтому построение адекватных и эффективных математических моделей указанных процессов является определяющим при создании компьютерной модели газонаполненного сепаратора.

В разработанных к настоящему времени математических моделях газонаполненных сепараторов процессы флуктуаций ионного заряда трактуются либо в одноэлектронном приближении [3, 4], либо вообще не обсуждаются [5]. Учет захвата и потери ионом только одного электрона при принятой в работах [3, 4] аппроксимации сечений этих процессов приводит к симметричным распределениям по зарядам ионов в пучке. Между тем экспериментальные данные свидетельствуют о наличии заметной асимметрии в равновесных зарядовых распределениях ионов в МэВ-диапазоне энергий при их прохождении через ве- ионов пучка в фокальной плоскости сепаратора.

щество [6–8]. Кроме того, в указанном диапазоне энергий сечения потери ионом двух и более электронов при столкновении с молекулой газа становятся сравнимыми с сечениями захвата и потери одного электрона [6].

В настоящей работе предлагается математическая модель флуктуации ионного заряда при столкновениях с молекулами газа, учитывающая процессы захвата одного электрона и процессы потери одного или двух электронов. Исследуется влияние флуктуации ионного заряда на распределение ионов пучка в фокальной плоскости сепаратора.

СРЕДНИЙ РАДИУС КРИВИЗНЫ ТРАЕКТОРИИ В МАГНИТЕ

В дипольном магните радиус кривизны траектории иона массы m с зарядом q равен р = mv / qB,                (1)

где v — составляющая скорости иона, ортогональная вектору магнитной индукции B . Пусть q = q n + A q , где q n — номинальное значение заряда, соответствующее магнитной жесткости, на которую настроен дипольный магнит. Обычно настройка ведется на величину среднего равновесного заряда q n = q .

Полагая Aq / qn << 1 и раскладывая (1) в ряд Тейлора в окрестности qn , имеем те

р(q) = Pn У(-Aq / qn)k, k=0

где p n = mvI q_nB — номинальное значение радиуса кривизны траектории. Усредняя по распределению заряда и учитывая, что q n = q , получаем

∞ p=pn 2 (-a q1 q) k • к=0

Для симметричного относительно среднего значения распределения заряда при нечетных значениях к выполняется ( A q ) ^k = 0, и в сумме остаются только положительные слагаемые. Поэтому p >  p n , и превышение среднего радиуса кривизны по сравнению с номинальным значением тем больше, чем меньше среднее равновесное значение заряда и чем шире распределение. Заметим, что торможение ионов в газе приводит к уменьшению радиуса кривизны траектории, и в этом смысле потери энергии и симметричные флуктуации заряда — противоположно действующие факторы.

Для несимметричных распределений (с отличными от нуля нечетными центральными моментами) среднее значение радиуса кривизны траектории может быть как больше, так и меньше номинального значения.

Приведенное выше рассмотрение свидетельствует о необходимости разработки в рамках общей модели газонаполненного сепаратора математической модели флуктуации ионного заряда, учитывающей многоэлектронные процессы, приводящие к асимметрии равновесного распределения зарядов в пучке.

КИНЕТИКА ФЛУКТУАЦИЙ ИОННОГО ЗАРЯДА

При движении иона со скоростью v в газовой среде флуктуации его заряда описываются кинетическим уравнением dFq (t)

—/ = 2 ["(qq)Fq' (t) - а(q, q3Fq (t)], (2) d t ■ где Fq (t) — вероятность зарядового состояния q в момент времени t, 2_Fq = 1; а (q', q) = = n7(q', q)v — частота столкновений иона с молекулой газа с переходом из зарядового состояния q' в зарядовое состояние q, 7(q', q) — соответствующее сечение перехода, n — концентрация молекул среды. Величину Fq можно считать долей ионов в пучке в зарядовом состоянии q.

Следует отметить, что сечение перехода 7(q', q), входящее через а(q', q) в уравнение (2), относится к основному состоянию иона. Это на- кладывает ограничение на плотность газовой среды: она должна быть достаточно мала, чтобы среднее время между столкновениями 1I а было больше времени релаксации иона, возбужденного в результате предыдущего столкновения. В противном случае в уравнении (2) необходимо учитывать зависимость сечения перехода от электронного состояния иона. Вопрос о влиянии плотности газовой среды на средний равновесный ионный заряд обсуждался в работе [9].

Если скорость иона постоянна, то удобнее в уравнении (2) от времени перейти к величине x = tvn — "толщине" мишени. Тогда dFq (x) хч /,

——= 2 ^{[ 7 (} q , q ) Fq' ⁽ x ) ^{- 7 (} q , q ) ^F q ⁽ x ^)].

dx

Равновесное, не зависящее от x зарядовое распределение F ( q ) = F_q ( ” ) определится из соотношения

2[7(q', q)F (q') - 7(q, q')F (q)] = 0, q′≠q

Кроме того, для равновесного распределения при произвольной фиксированной величине заряда q должно выполняться

2 ^{[ F (} q ^{, ) 7 (} q ‘ , q ‘ ) - ^{F (} q ^{,,) 7 (} q " q q ^{, ) ]}= ⁰.      ⁽⁴⁾

q ′< q ≤ q ′′

Отсюда, если ограничиться одноэлектронными процессами, когда | q ' - q | = 1, для равновесного распределения F ₀( q ) получаем

^F 0 ⁽ q ⁾⁷i ⁽ q ) = ^F 0 ⁽ q + ^{1) 7} _C ⁽ q + 1),        ⁽⁵⁾

где 7 c ( q ) — сечение захвата, а 7 _l ( q ) — сечение потери одного электрона.

Если, следуя работам [3, 4], принять экспоненциальную аппроксимацию для сечений:

⁷ c ⁽ q ) = A c ^exp⁽ a c ⁽ q - q 0 ));

(6) 7i(q) = Al exP(-al(q - q0)), то соотношению (5) удовлетворяет гауссово распределение [6]

F 0 ( q ) = (iMi n d 0 )exp{ - ( q - q )I2 d 02 },      (7)

где

1I d 02 = a c + a i , A i = A c exp[( « c - a )I2]. (8)

В этих формулах q — текущее значение заряда, q = q ₀ — среднее равновесное значение заряда иона, d ₀ — стандартное отклонение гауссова распределения.

Простейшим обобщением модели одноэлектронных процессов флуктуации ионного заряда является дополнительный учет процессов потери двух электронов. Как отмечалось в работах [6–8], такой процесс является весьма вероятным в МэВ-диапазоне энергий.

Обозначим сечение потери ионом в столкновении двух электронов ст 2 l ( q ). Тогда соотношение (4) для равновесного распределения принимает вид

F ⁽ q ^{) [ ст} 1 ⁽ q ) + ^ст 2 1 ⁽ q ^{) ]} + F ⁽ q - ^{1) ст} 2 1 ⁽ q - 1) =

= F ⁽ q + 1) ст _с ⁽ q + 1).

Отсюда, учитывая соотношение (5), имеем

F ( q + 1) = F о ( q + 1) +

F ( q )       F 0 ( q )

+ ст ₂,( q ) + Fq ^-» ст₂, 2 l                              2 l

L           F ( q )

ст ⁽ q + 1).

Второе слагаемое в правой части соотношения (9) зависит от сечений потери двух электронов. Поскольку это слагаемое положительно, равновесное распределение F ( q ) при q <  q m растет быстрее, а при q >  q m убывает медленнее соответствующего гауссова распределения (7). Это п р иводит к сдвигу среднего равновесного заряда q относительно q ₀ и к появлению асимметрии в равновесном распределении.

Естественно предположить, что сечение ст ₂ l ( q ) потери двух электронов, как и сечение ст ₁ ( q ) потери одного электрона, убывает с ростом величины положительного заряда иона q : вероятность отрыва последующих электронов от иона при столкновении уменьшается с уменьшением числа оставшихся электронов. Поэтому в качестве аппроксимации ст ₂ l ( q ) примем выражение, аналогичное выражению (6):

^ст 2 1 ⁽ q ) = A 2 1 exp⁽ - a 2 1 ⁽ q - q o ))-       ⁽¹⁰⁾

В соответствии с принятыми аппроксимациями (6) и (10) в нашей модели имеется семь параметров A_c , a_c , A_l , a_l , A _{2 l} , a _{2 l} , q ₀ , из которых вследствие соотношений (8) и условия нормировки для вероятностей перехода независимых остается четыре.

РЕЛАКСАЦИЯ ЗАРЯДОВОГО РАСПРЕДЕЛЕНИЯ К РАВНОВЕСНОМУ

Представим процесс изменения зарядового состояния иона при движении в газовой среде в виде однородной цепи Маркова {п 0, T} с числом со стояний z +1. Здесь п0— вектор распределения начальных зарядовых состояний, T = {pik} — матрица вероятностей перехода, pik — вероятность перехода из состояния с зарядом q = i в состояние с зарядом q = k (i,к = 0,1,...,z), z — атомный номер иона.

Вероятности переходов определятся из соотношений

P c ⁽ q ) = ст ⁽ q )/ ст ⁽ q );

P i ⁽ q ) = ст ⁽ q ) kt ⁽ q );             ⁽¹¹⁾

p 21(q) = ст 21(q) kt(q), где стt(q) = стс(q) + ст1(q) + ст 21(q) —       (12)

полное сечение изменения заряда.

В соответствии с выбранной моделью, учитывающей захват ионом одного электрона и отрыв от него одного или двух электронов (формулы (6) и (10)), переходная матрица T трехдиагональна: для каждого данного состояния с q = i >  0 отличны от нуля вероятности переходов только в состояния с q = i - 1, i + 1 , i + 2.

Вектор распределения зарядовых состояний после n переходов пn =(tТ)nп0 =(tn )Тп0,

Т где T — транспонированная матрица перехода.

В соответствии с теоремой об асимптотическом поведении (см., например, [10], с. 286) в случае положительной матрицы перехода существует предельный вектор состояний п = lim n _z^ п n , не зависящий от начального состояния π ₀ . Этот вектор является собственным вектором матрицы M = lim n ,„ ( t ^т ) n с характеристическим числом 1. Матрица М состоит из одинаковых столбцов, каждый их которых совпадает с предельным вектором зарядовых состояний π .

В нашем случае матрица Т является лишь неотрицательной. Однако численные эксперименты показали, что для широкого диапазона значений параметров нашей модели предельная матрица М существует. Скорость сходимости зависит от величины относительной доли "перемешивающего" члена p _{2 l} ( q ) в матрице перехода.

Задавшись порядком малости элементов матрицы перехода £ , мы фиксируем ее размерность. В частности, при е = 10-4 размерность матрицы перехода 9x9, при е = 10-5 — 12x12, при е = 10-7 — 17×17. Примем в качестве критерия установления процесса сходимости ту же величину е . Численные эксперименты показали, что при Ac = Al, A2l = Al /2 Для получения предельной матрицы, а тем самым и равновесного зарядового распределения требуется: 20 переходов при е = 10-4, 25 переходов при е = 10-5 и 35 переходов при е = 10 -7. Если уменьшать долю p2l (q) , необходимое число переходов возрастает. Так, при A2l = Al /4 и е = 10-5 для достижения равновесного распределения требуется уже 60 переходов.

Определив матрицу М , мы находим равновесное зарядовое распределение π , для которого в работе вычислялись среднее значение равновесного заряда q , дисперсия d ² и коэффициент асимметрии $ = ц ₃/ d ^3/2, где ц ₃ — третий центральный момент. Именно эти параметры приводятся в качестве экспериментальных данных по зарядовым распределениям пучков ионов при их прохождении через вещество [6–8]. Сопоставление вычисленных нами значений моментов с этими экспериментальными данными позволяет выбрать значения параметров нашей модели.

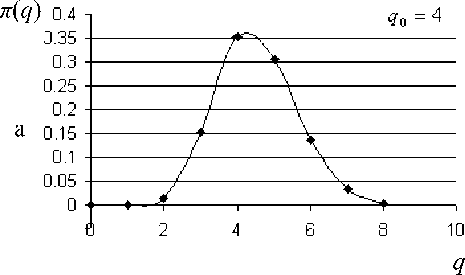
На рис. 1 в качестве примера представлены равновесные зарядовые распределения, вычисленные на основе описанной выше методики при A c = A l , A 2 _l = A l /2, a c = a l = 1, a 2 _l = 0.5 для трех значений q ₀ . Все три распределения имеют примерно одинаковые ширины: стандартное отклонение d = 1.1 и заметный коэффициент асимметрии $ = 0.28. Заметим, что для одноэлектронного приближения с гауссовым равновесным распределением (7) соотношение (8) для выбранных значений параметров дает d ₀ = 1.0 и $ ₀ = 0.

РАСПРЕДЕЛЕНИЕ ИОНОВ В ПЛОСКОСТИ ПРИЕМНИКА СЕПАРАТОРА

Модель флуктуации ионного заряда является составной частью компьютерной модели газонаполненного сепаратора. Она реализована в виде монте-карловской процедуры. При влете иона в газонаполненный тракт сепаратора ему случайным образом приписывается заряд в соответствии с экспериментально определенным начальным зарядовым распределением. Заряд иона постоянен на длине свободного пробега l , которая ген е рируется в соответствии с соотношением l = - X ln R , ( R — равномерно распределенное на промежутке [0,1) случайное число). В точке столкновения заряд иона изменяется в соответствии с вероятностями перехода (11).

В нашей модели параметр о м является средняя длина свободного пробега X , которая связана

π ( q )

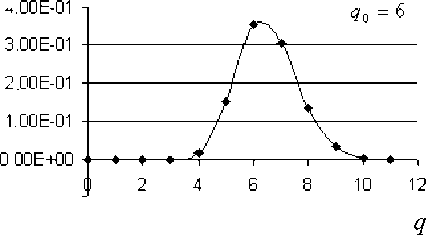
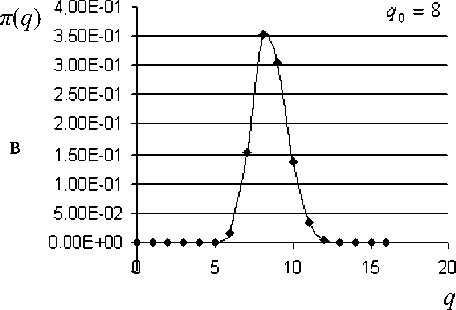
Рис. 1. Равновесные зарядовые распределения ^{п (}q ) при A c = A i , A 2 1 = A i /2, a = a = 1, a 2 ₁ = 0.5 для различных значений q ₀: а — 4, б — 6, в — 8

с полным сечением a t процесса изменения заряда (12) и с концентрацией n молекул газа соотношением X = 1/( n a t ). В программе задается X и отношение между амплитудами сечений A_c , A_l и A _{2 l} в соотношениях (6) и (10).

Экспериментальные оценки [11] показывают, что тяжелый ион со средней энергией в несколько десятков МэВ при движении в газе при давлении p = 1 торр ( n ~ 3 х 10¹⁶ см ^{- 3}) изменяет

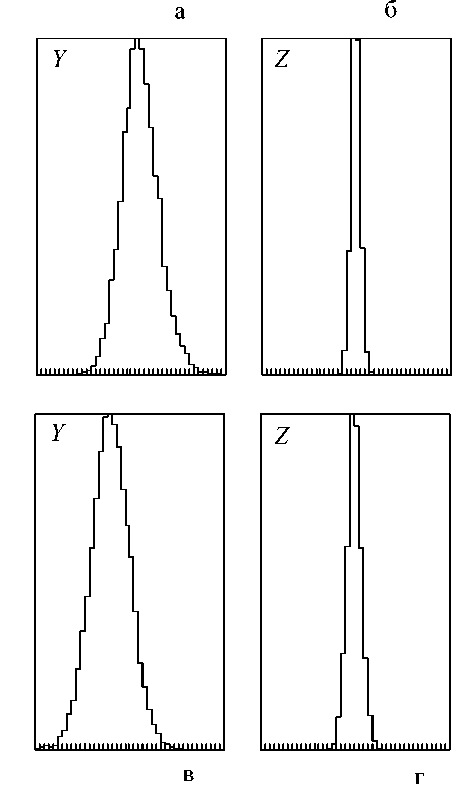
Рис. 2. Распределение ионов в области приемника газонаполненного сепаратора в вертикальном ( Y ) и в горизонтальном ( Z ) направлениях при a c = a l = a 2l = 2 (узкое зарядовое распределение) без учета двухэлектронных процессов (а, б) и с учетом двухэлектронных процессов (в, г)

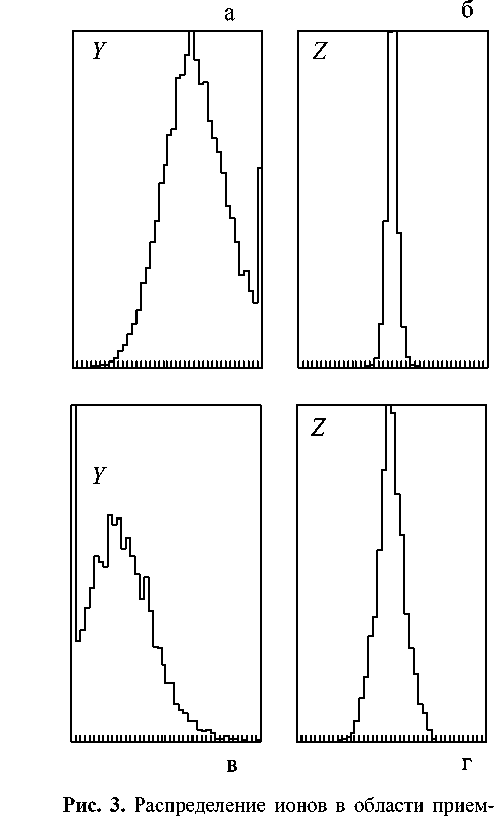
ника газонаполненного сепаратора в вертикальном ( Y ) и в горизонтальном ( Z ) направлениях при a c = a l = a 2 l = 0.4 (широкое зарядовое распределение) без учета двухэлектронных процессов (а, б) и с учетом двухэлектронных процессов (в, г)

свое зарядовое состояние при атомных столкновениях 100–1000 раз на 1 м пу т и. Это означает, что длина свободного пробега X лежит в пределах 0.1–1.0 см.

На рис. 2 и 3 представлены рассчитанные гистограммы пространственного распределения ионов с массой 254 а.е. после прохождения сепаратора, заполненном водородом с давлением 1 торр. Сепаратор построен по схеме DQhQv и состоит из дипольного магнита D и расположенных за ним квадрупольных линз, фокусирующих в горизонтальном (Qh ) и в вертикальном (Qv ) направлениях. Ионно-оптическая схема и геометрические размеры соответствуют газонаполненному сепаратору Лаборатории ядерных реакций ОИЯИ (Дубна) [5]. Длина первого бесполевого промежутка в нем составляет 39.5 см, поэтому равновесное зарядовое распределение ионов устанавливается уже до входа в дипольный магнит.

Гистограммы распределений рассчитаны в плоскости приемника в горизонтальном (Y — в плоскости дисперсии) и в вертикальном (Z) направлениях. Диапазон изменения координат Y и Z одинаков: –100÷100 мм. Значения параметров сечений изменения заряда ac = al = a 2 l = 2.0 (рис. 2) соответствуют узкому равновесному зарядовому распределению: соответствующее гауссово распределение при одноэлектронных процессах имеет стандартное отклонение d0 = 0.5 . Значения параметров ac = al = a2l = 0.4 (рис. 3) соответствуют широкому равновесному зарядовому распределению — d0 = 1.1 .

Первый ряд гистограмм (а, б на рис. 2 и 3) соответствует одноэлектронным процессам ( A _{2 l} = 0 ). Второй ряд гистограмм (в, г на рис. 2 и 3) соответствует дополнительному учету потери двух электронов. Отметим кардинальное изменение гистограмм: Y- и Z- распределения уширились и Y- распределение сместилось в сторону меньших значений.

Уширение пространственных распределений обусловлено уширением равновесных зарядовых распределений при учете двухэлектронных процессов. Характеристики равновесных зарядовых распределений на входе в дипольный магнит для узкого зарядового распределения (рис. 2): q ₀ = 6.7 , d ₀ = 0.5 , s ₀ = 0 — при учете только одноэлектронных процессов; q = 7.0 , d = 0.86, s = 0.25 — при учете двухэлектронных процессов. Соответствующие характеристики для широкого зарядового распределения (рис. 3): q ₀ = 6.7 , d ₀ = 1.1 , s ₀ = 0 — при учете только одноэлектронных процессов; q = 7.6 , d = 1.4 , s = 0.14 — при учете двухэлектронных процессов. Таким образом, учет потери двух электронов приводит к увеличению среднего заряда и дисперсии распределения и к появлению отличной от нуля асимметрии.

Сдвиг Y- распределений в сторону меньших значений обусловлен двумя причинами. Во-первых, описанным в первом разделе работы уменьшением среднего радиуса кривизны траектории ионов в дипольном магните в случае наличия асимметрии в зарядовом распределении по сравнению со средним радиусом кривизны траектории ионов с симметричным зарядовым распределением при прочих равных условиях. И, во-вторых, увеличением среднего равновесного заряда при учете двухэлектронных процессов по сравнению со средним равновесным зарядом при учете только одноэлектронных процессов.

ВЫВОДЫ

• 1.    В случае симметричных зарядовых распределений ионов в пучке флуктуации ионного заряда приводят к увеличению среднего радиуса кривизны траектории иона в магнитном поле. Для зарядовых распределений с асимметрией средний радиус кривизны траектории в магнитном поле мо-

• жет как увеличиваться, так и уменьшаться.

• 2.    Предложена математическая модель флуктуации ионного заряда при столкновениях с молекулами газа, учитывающая процессы захвата одного электрона и процессы потери одного или двух электронов. Эта модель, являющаяся простейшим обобщением модели одноэлектронных процессов флуктуации, приводит к существенному изменению равновесных зарядовых распределений, включая появление асимметрии в распределениях, отсутствующей в модели одноэлектронных процессов.

• 3.    На основе численного моделирования движения ионов в газонаполненных сепараторах показано, что учет двухэлектронных процессов приводит к уширению пространственных распределений ионов пучка в фокальной плоскости сепаратора и к их сдвигу, что необходимо учитывать при калибровке компьютерной модели газонаполненного сепаратора.