Компьютерное моделирование и рентгеноструктурный анализ углеродных нанотрубок

Задача исследования углеродных материалов в некристаллическом состоянии рентгенографическими методами далеко не тривиальна [9]. Причина в том, что из-за большого разнообразия типов связи атомов углерода и его полиморфных модификаций [10] эти материалы в некристаллическом состоянии трудно идентифицировать и тем более определить особенности структурного состояния отдельных составляющих.

Тем не менее существует принципиальная возможность идентификации различных полиморфных модификаций углерода дифракционными методами исследования [8]. Один из подходов к решению данной задачи лежит в области компьютерного моделирования атомной структуры. Он заключается в построении ряда моделей различных углеродных материалов и расчете теоретических дифракционных картин рассеяния для них [7], [9]. Выявленные на полученных картинах особенности максимумов интенсивности (форма, размытие, асимметрия, в ряде случаев смещение)

дают информацию, позволяющую проводить определение различных структурных состояний углерода в экспериментальном образце [2].

Основная цель данной работы – попытка применения данного метода к идентификации углеродных нанотрубок, а также к оценке их характеристик [2], [16] (типа, числа слоев, степени хиральности, радиуса, длины) по имеющимся рентгенограммам образцов углеродсодержащих материалов.

В данной статье:

• 1.    Разработаны алгоритмы [3], [5] и построены модели однослойных (ОУНТ) и многослойных (МУНТ) углеродных нанотрубок различных конфигураций;

• 2.    Проанализированы теоретические дифракционные картины рассеяния, рассчитанные для сформированных моделей;

• 3.    Произведено сравнение рассчитанных картин рассеяния с экспериментом, выполненным для образца углеродного материала, содержащего УНТ.

Основной параметр, используемый при построении моделей УНТ, – индексы хиральности [1], [2], [3], [5], [16]. Они определяют все основные характеристики нанотрубок, а также дискретность их изменения. Заметим, что невозможно существование УНТ абсолютно произвольных конфигураций [2].

В работе были построены модельные ОУНТ, а также МУНТ двух основных наблюдаемых в эксперименте типов: «русская матрешка» и «свиток» [5], [12], [15]. Известно, что в МУНТ величина межслоевого расстояния должна находиться в допустимых для углеродных материалов (с sp2-гибридизацией валентных орбиталей [10]) пределах (3,354–3,600 Å). Кроме того, расстояние между двумя соседними слоями остается постоянным в пределах всей трубки лишь для пяти степеней хиральности: 0 («зиг-заг»), 0,2, 0,3, 0,4 и 0,5 («кресло») [1], [5]. Соответственно, особенностями МУНТ «свиток» являются незамкнутость структуры [12], а также допустимость для него лишь пяти степеней хиральности (характеризующихся постоянством межслоевого расстояния) [1], [5]. Следует отметить, что при одинаковых внешних и внутренних радиусах число слоев у «русской матрешки» на один больше, чем у «свитка» [5].

В основе вычисления теоретических дифракционных картин рассеяния лежит известная методика Дебая по расчету порошковых дифрак-тограмм [6], [12]. В результате рассчитываются интенсивность рассеяния I(S), S-взвешенная интерференционная функция рассеяния H(S), где S = 4πsinθ/λ – длина дифракционного вектора, а также функция парного взаимодействия D(R) [2], [7], [8]. При анализе полученных рентгенограмм в качестве критерия достоверности была использована функция H(S), как более информативная по сравнению с распределением интенсивности [2], [5].

ВЛИЯНИЕ ДЛИНЫ И ТИПА УНТ НА КАРТИНУ РАССЕЯНИЯ

В работе [2] было установлено, что характер изменения расстояния между соседними слоями МУНТ (постоянство, переменчивость) не оказывает какого-либо существенного качественного влияния на картину рассеяния, которое можно было бы идентифицировать по характеру пиков на H(S). Поэтому для упрощения расчетов в дальнейшем производилось моделирование МУНТ с постоянным межслоевым расстоянием.

С целью анализа изменений картин рассеяния для УНТ различной длины были сформированы модели:

• a)    ОУНТ с индексами хиральности (20, 10) (радиус ~6,78 Å), длиной от 5 до 500 Å;

• b)    МУНТ («русская матрешка» и «свиток»), образованные из 4 слоев, с индексами хиральности внутреннего слоя (20, 10) (внутренний радиус ~6,78 Å), длиной от 5 до 500 Å.

Анализ рассчитанных дифракционных картин показал, что при изменении длины УНТ характер и положения пиков на H(S) сохраняются, но интерференционный максимум при длине дифракционного вектора S ~5,2 Å-1 (соответствует отражению графита 110) становится высоким и узким. Это, очевидно, связано с периодичностью в расположении атомов в направлениях, параллельных оси формируемой модели.

Для выявления характерных особенностей на рентгенограммах УНТ различных типов были сформированы следующие модели:

• a)    ОУНТ типа «кресло», радиус ~13,56 Å (индексы хиральности (40, 20)), длина ~75 Å;

• b)    МУНТ «русская матрешка» типа «кресло» с числом слоев, равным 4, внутренний радиус ~13,56 Å (индексы хиральности (40, 20)), длина ~75 Å;

• c)    МУНТ «свиток» типа «кресло», внутренний радиус ~13,56 Å (индексы хиральности (40, 20)), внешний радиус ≈23,73 Å (3 витка), длина ~75 Å.

Результаты расчета H(S) для данных моделей (рис. 1) показывают, что по дифракционным картинам имеется возможность идентифицировать УНТ различного типа. Так, на рентгенограмме для модели ОУНТ (рис. 1a) отсутствуют максимумы, соответствующие отражениям графита типа (00l) [13], наблюдаемые на дифракционных картинах для моделей МУНТ (рис. 1b и 1c).

H(S)

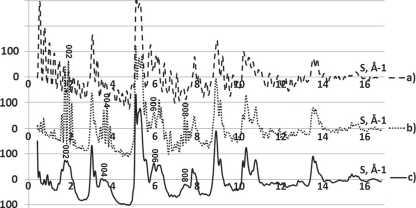
Рис. 1. Сравнение s-взвешенных интерференционных функций H(S) для моделей ОУНТ (a), МУНТ «русская матрешка» (b) и МУНТ «свиток» (c)

Обратим внимание также на то, что на H(S) для ОУНТ (рис. 1a) наблюдаются осцилляции с малым периодом. Причиной возникновения данных осцилляций является замкнутость структуры.

Кривая H(S) для модели «русской матрешки» (рис. 1b) отличается от H(S) для модели «свитка» (рис. 1c) лишь осциллирующим характером H(S) [4]. Здесь возникновение осцилляций связано не только с замкнутостью структуры, но и с дискретностью изменения радиусов кривизны цилиндрических поверхностей различных слоев, что приводит к небольшому различию в расстояниях между атомами, принадлежащими разным поверхностям МУНТ «русская матрешка». Именно поэтому в МУНТ осцилляции более «упорядочены» по положению на H(S).

Видно (рис. 1), что наблюдаемые на рентгенограммах осцилляции возникают лишь в замкнутых УНТ (ОУНТ и МУНТ «русская матрешка»), в то время как в незамкнутом «свитке» нет резких изменений радиуса, что приводит к отсутствию соответствующих «шумов». При этом оказалось, что чем больше радиус трубки, тем меньший период имеют осцилляции, как в ОУНТ, так и в МУНТ.

Устранить наблюдаемые на H(S) осцилляции можно путем усреднения картин рассеяния [4], рассчитанных для моделей УНТ различного внутреннего радиуса. Так, были построены УНТ типа «кресло» длиной 75–100 Å в диапазоне изменения радиуса внутреннего слоя 5–15 Å: a) ОУНТ; b) МУНТ «русская матрешка», 4 слоя; c) МУНТ «свиток», 3 витка. Соответствующие «усредненные» H(S) приведены на рис. 2.

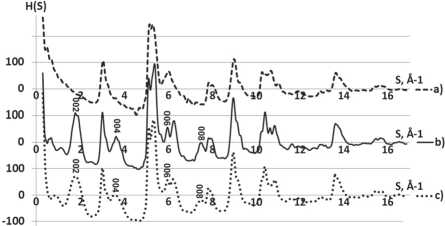
Рис. 2. Сравнение «усредненных» s-взвешенных интерференционных функций H(S) для моделей ОУНТ (a), МУНТ «русская матрешка» (b), МУНТ «свиток» (c)

В результате выполненного «усреднения» (рис. 2) основные осцилляции и «шумы» уходят и можно четко определить характер и положения интерференционных максимумов. Заметим, что введенное «усреднение» влияет лишь на осцилляции и «шумы», не затрагивая характер рентгенограмм и пиков интенсивности (рис. 1).

Это позволяет однозначно отличить ОУНТ и МУНТ. Разница на «усредненных» кривых H(S), рассчитанных для трубок типа «русская матрешка» и «свиток», заключается лишь в отличиях ширины пиков, соответствующих отражениям типа (00l). Моделирование трубок с большим числом слоев (6 и более) и расчет картин рассеяния показал, что данная разница становится несущественна и отличить «усредненные» H(S) для моделей смеси МУНТ различных типов по полученной рентгенограмме представляется затруднительным.

Как правило, в реальном эксперименте в облучаемом объеме образца присутствует очень много различных по характеристикам нанотрубок, что приводит к сглаживанию картин рассеяния и отсутствию наблюдаемых на модельных рентгенограммах осцилляций. Поэтому при усреднении H(S) для различных по геометрическим характеристикам модельных нанотрубок получаются картины рассеяния, соответствующие возможным экспериментальным рентгено- граммам от ОУНТ и МУНТ, которые могут быть использованы при их идентификации.

ВЛИЯНИЕ ХИРАЛЬНОСТИ, ВНУТРЕННЕГО РАДИУСА, ЧИСЛА СЛОЕВ УНТ НА КАРТИНУ РАССЕЯНИЯ

Для выявления идентификационных признаков на картинах рассеяния УНТ различной степени хиральности были смоделированы два граничных типа трубок: «зиг-заг» и «кресло» [1], [2], [3], [5], [16].

Для МУНТ было произведено усреднение H(S) для моделей длины 100–120 Å, состоящих из 4 слоев, в диапазоне изменения радиуса внутреннего слоя 5–50 Å. Результат сравнения H(S), рассчитанных для МУНТ типа «кресло» и «зигзаг», представлен на рис. 3.

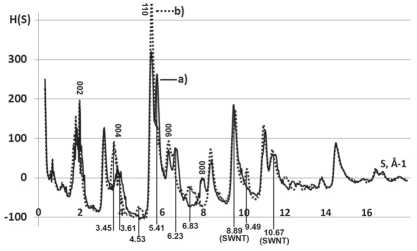
Рис. 3. Сравнение «усредненных» s-взвешенных интерференционных функций H(S) для моделей МУНТ типа «зиг-заг» (a) и «кресло» (b)

На «усредненных» зависимостях H(S) для МУНТ различной степени хиральности виден ряд существенных отличий (рис. 3):

• 1.    На кривой H(S), рассчитанной для УНТ типа «кресло», максимум (004) имеет меньшую величину и смещен по S вправо на ≈0,15 Å^-1 по сравнению с аналогичным максимумом на кривой H(S), рассчитанной для УНТ типа «зиг-заг»;

• 2.    Максимум (110) на H(S), рассчитанной для трубок типа «зиг-заг», существенно выше, нежели на H(S), рассчитанной для трубок типа «кресло»;

• 3.    На кривой H(S), рассчитанной для УНТ типа «кресло», максимумы (110), (006) более широкие и имеют существенное расщепление на два: возникают максимумы при S ~5,41 Å^-1, S ~6,23 Å^-1 соответственно;

• 4.    На кривой H(S) для трубок типа «зиг-заг» не наблюдается максимум (008);

• 5.    На кривой H(S), рассчитанной для УНТ типа «зиг-заг», имеются небольшие максимумы в положениях S ~4,53 Å^-1, S ~6,83 Å^-1, S ~9,49 Å^-1.

При построении моделей ОУНТ радиуса 5–15 Å различной степени хиральности оказалось, что на характере H(S) степень хиральности проявляется:

• 1.    Наличием на рентгенограмме от трубок типа «кресло» расщепления пика интенсивности

• (110)    (рис. 3), отсутствующего на кривой H(S), рассчитанной для УНТ типа «зиг-заг».

• 2.    Отсутствием на рентгенограмме от трубок типа

• 3.    Более существенным расщеплением пика при S ~10,67 Å^-1 (рис. 3) на кривой H(S), рассчитанной для ОУНТ типа «зиг-заг», нежели на H(S) для ОУНТ типа «кресло».

«кресло» расщепления пика интенсивности при S ~ 8,89 Å-1 (рис. 3), имеющегося на кривой H(S), рассчитанной для УНТ типа «зиг-заг».

При расчете рентгенограмм для хиральных нанотрубок получаемые картины будут тем ближе к H(S), рассчитанной для трубок типа «зиг-заг» (рис. 3a), или к H(S), рассчитанной для трубок типа «кресло» (рис. 3b), чем степень хиральности моделируемых трубок будет ближе к 0 или к 0,5 соответственно [4].

Для определения влияния внутреннего радиуса УНТ на характер H(S) были смоделированы УНТ (как однослойные, так и многослойные) типа «кресло» длины ~100 Å в диапазоне изменения внутреннего радиуса от 5 до 15 Å (для ОУНТ) и от 5 до 50 Å (для МУНТ). Выбранные диапазоны изменения внутреннего радиуса соответствуют параметрам экспериментально получаемых образцов УНТ [12]. Анализ рассчитанных для данных моделей рентгенограмм показал, что изменение внутреннего радиуса в таких диапазонах не может быть однозначно идентифицировано на зависимостях H(S) по характеру или величине интерференционных максимумов. Единственное значимое изменение – уменьшение периода осцилляций на H(S) (как для ОУНТ, так и для МУНТ «русская матрешка»).

Для выявления характерных особенностей на рентгенограммах УНТ, содержащих различное число слоев, были построены модельные МУНТ типа «кресло» степени хиральности 0,3, внутреннего радиуса ~25 Å, длины ~100–120 Å с числом слоев от 2 до 30. В результате анализа полученных картин рассеяния было установлено, что с увеличением числа слоев, существенно возрастают интерференционные максимумы, соответствующие отражениям графита типа (00l) (рис. 4b), то есть в тех областях H(S), где раньше наблюдались осцилляции (рис. 4a).

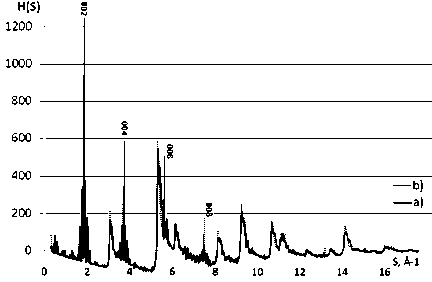
Рис. 4. Интерференционные функции H(S) для МУНТ «кресло»: Rвнутр ~25 Å, длина ~100 Å, число слоев равно 5 (a) и 20 (b)

При большом числе слоев (16 и более) пики интенсивности в положениях отражений 00l представлены в виде узких линий [4] (рис. 4b). При этом наибольшее возрастание интенсивности наблюдается у пиков, соответствующих отражениям (002) и (004) (рис. 4b).

ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ

УГЛЕРОДНЫХ МАТЕРИАЛОВ, СОДЕРЖАЩИХ УНТ

Для иллюстрации возможности применения описанной методики и построения моделей атомных конфигураций при анализе экспериментальных образцов углеродных материалов, были проведены рентгенографические исследования образцов углеродных материалов, полученных от « Arry Nano Inc. » [12], предположительно содержащие многослойные углеродные нанотрубки длиной 1–2 мкм и внешнего радиуса 50–100 Å. Рентгенографирование выполнено в MoKα излучении в геометрии на просвет в интервале углов 2–145^о, кристалл-монохроматор был установлен в первичных лучах.

Наиболее близкой к эксперименту была H(S) для модели смеси из 4-слойных МУНТ типа «кресло» длины ~50–200 Å, внешнего радиуса ~50–100 Å. На рис. 5 приведены интерференционные функции H(S) экспериментального образца и модели смеси МУНТ.

Наличие на экспериментальной кривой (рис. 5) интерференционных максимумов (002) и (004) говорит о присутствии в образце слоистых углеродных структур с межслоевым расстоянием 3,354–3,600 Å [1], [4], [14]. Однако на экспериментальной и модельной кривых (рис. 5) имеется ряд областей, в которых видно различие.

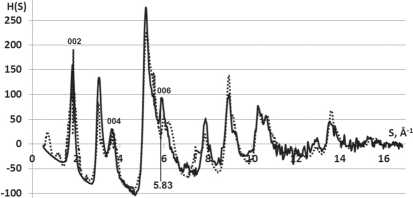
modeled mix of MWNT ---experimental data

Рис. 5. Интерференционные функции H(S) экспериментального образца и подобранной возможной теоретической модели

Так, при длине дифракционного вектора S ~5,83 Å-1 (рис. 5) наблюдается расщепление максимума (006) на модельной кривой, отсутствующее на экспериментальной зависимости. Очевидно, это связано с тем, что выбранная модель содержит лишь МУНТ «кресло», в то время как экспериментальный образец может содержать МУНТ различной степени хиральности (рис. 3). То же самое относится и к другим максимумам интенсивности на протяжении всей длины дифракционного вектора S.

Для оценки количественного соответствия полученной экспериментальной и модельной картин рассеяния воспользуемся следующим фактором недостоверности (R-фактором) [14]:

„ Х [₌^т₁ |^ эксп_;^_ ^ мод_г |

К = у~т b I , ^,=1|^экспг| где Nт – число точек на кривой функции распределения интенсивности I(S).

Зависимость I(S) была взята вполне закономерно, так как на ее основе рассчитывается кривая H(S), используемая для качественного сравнения дифракционных картин рассеяния.

Для подобранной модели R-фактор равен ~0,2. Для получения меньшего значения R (более достоверной кривой H(S)) необходимо произвести варьирование параметров модельных УНТ в смеси в более широком диапазоне, а также учесть возможное наличие примесей в исследованном образце.

ЗАКЛЮЧЕНИЕ

В работе построены модельные УНТ различных конфигураций и рассчитаны теоретические дифракционные картины для них. Показано, что модельные рентгенограммы для УНТ различного типа имеют ряд особенностей на кривых H(S), по которым данные нанотрубки можно идентифицировать, а в ряде случаев также приближенно оценить их характеристики. Проведенные рентгенографические исследования образца углеродного материала и построенная модель атомной структуры, картина рассеяния для которой оказалась близка к экспериментальной рентгенограмме, показали, что задача идентификации УНТ в исследуемом образце в ряде случаев может быть решена применением рентгеноструктурного анализа и компьютерного моделирования атомной структуры. На нынешнем уровне производства и очистки нанотрубок получаемые образцы недостаточно «чистые», то есть содержат нанотрубки, различные по типу и размерам. Поэтому для достижения более надежных результатов идентификации необходимо комбинирование различных модельных УНТ (и их совокупностей) и расчет «усредненных» картин рассеяния от данных «смесей», а также введение искажения атомной структуры (тепловых колебаний, деформаций и т. д.).

БЛАГОДАРНОСТИ

Авторы выражают благодарность старшему преподавателю кафедры ФТТ ПетрГУ, к. ф.-м. н. Д. В. Логинову и профессору кафедры ФТТ ПетрГУ, к. ф.-м. н. Л. А. Алешиной за помощь при подготовке статьи.

* Исследования проведены в рамках Программы стратегического развития на 2012–2016 годы «Университетский комплекс ПетрГУ в научно-образовательном пространстве Европейского Севера: стратегия инновационного развития».

COMPUTER MODELING AND X-RAY DIFFRACTION ANALYSIS OF CARBON NANOTUBES