Компьютерное моделирование извлечения ионов из плазмы

Как известно [2], наиболее сложными задачами в проблеме математического моделирования ионных источников являются задачи моделирования ионно-электронных процессов в области ионизации и процессов извлечения ионов из плазмы. Помимо внешних полей, здесь большую, а подчас определяющую роль играет биполярный объемный заряд ионов и электронов.

В работе [1] была разработана методика моделирования ионно-электронных процессов во внешнем электрическом поле в приближении равновесного (больцмановского) распределения электронов для не слишком плотной плазмы, когда можно пренебречь парными кулоновскими корреляциями ионной компоненты. В этом приближении задача сводится к совместному решению кинетического уравнения Власова для одночастичной функции распределения ионов f ( r, p, t )

d f d t t + v d f d rr + F d f /dpp = 0          (1)

и уравнения Пуассона для электростатического потенциала u

A u = - 4 n e ( n i - n e ) .            (2)

Правую часть уравнения Пуассона составляет сумма плотностей объемного заряда ионной и электронной составляющих с концентрациями соответственно ni = n о i J fd3 P        и ne = n0e • exP[e(u - up )/kTe ] •

Здесь u_p и n _{0 e} — соответственно среднее значение потенциала и средняя концентрация электронов в области плазмы (ионообразования), T_e — электронная температура, n _{0 i} — средняя концентрация ионов.

ВЫЧИСЛИТЕЛЬНАЯ ПРОЦЕДУРА

Для решения этой системы нелинейных уравнений была предложена итерационная процедура, включающая в себя три вложенных друг в друга цикла итераций [1]. Внешние итерации — решение уравнения Власова методом моделирования ионных траекторий в поле, рассчитанном на предыдущем шаге итераций. Получаемый на этом этапе ансамбль траекторий служит для процедуры раздачи заряда ионной компоненты и формирования ионной составляющей правой части уравнения Пуассона. Следующий цикл итераций — решение уравнения Пуассона методом последовательной верхней релаксации (SOR). Поскольку уравнение Пуассона из-за наличия в правой части члена, описывающего электронную плотность и зависящего от потенциала, является нелинейным, процедура итераций метода SOR должна быть дополнена итерациями решения в каждом узле сетки нелинейного уравнения. В качестве такой процедуры была выбрана схема ньютоновских итераций. Они составили низший цикл итераций всей задачи.

Остановимся подробнее на этом цикле итераций. Переходя к безразмерным переменным ф = e(U - up )/kTe , x = r/ ^De , q = niln0e , где XDe = (kTe/4ne2n0e )12 — электронный дебаевский радиус, получаем уравнение Пуассона (2) в виде

A х ф = - q + ехр ( ф ) .

Для него система конечноразностных уравнений на двумерной сетке, построенных по пятиточечному шаблону, имеет вид

Ф0 = сф + с2Ф2 + сзФ3 + с4^4 - с5 [ехр(ф0 )- q], где ф0 — значение потенциала в рассматриваемом узле, ф1,...,ф4 — значения потенциала в соседних узлах, c1 ,…, c5 — коэффициенты, зависящие от геометрии и структуры сетки.

Последнее уравнение — уравнение относительно неизвестного ф0, является нелинейным. Для него схема ньютоновских итераций принимает следующий вид m+1

Ф 0 =

= ( ф 0 m -^ 5 ехр ( ф 0 m ) + c 1 Ф 1 + c 2 ф 2 + С з Ф 3 + С 4 Ф 4 + С 5 q ^{1 + С} 5 ^ех Р ⁽ Ф 0 m )

.

Здесь ф m ^{+ 1} — значение потенциала в рассматриваемом узле на ( m + 1 ) -й ньютоновской итерации, ф m — на предыдущей итерации.

Как показали численные эксперименты, итерационная схема оказалась устойчивой и обеспечила сходимость при относительной точности 10 ^{- 4} за

в

г

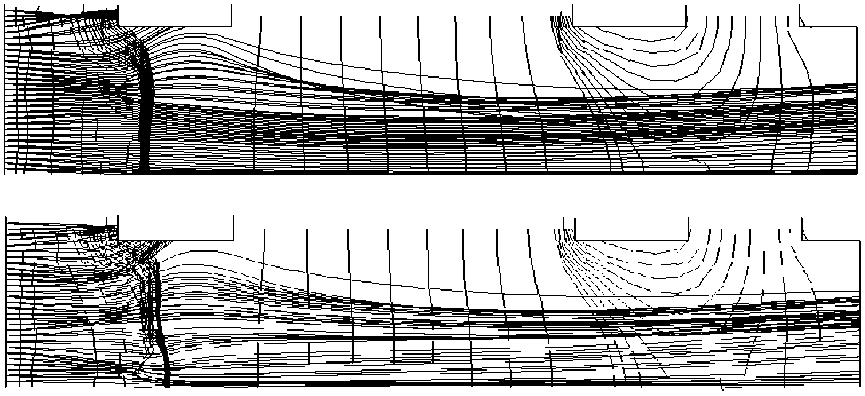
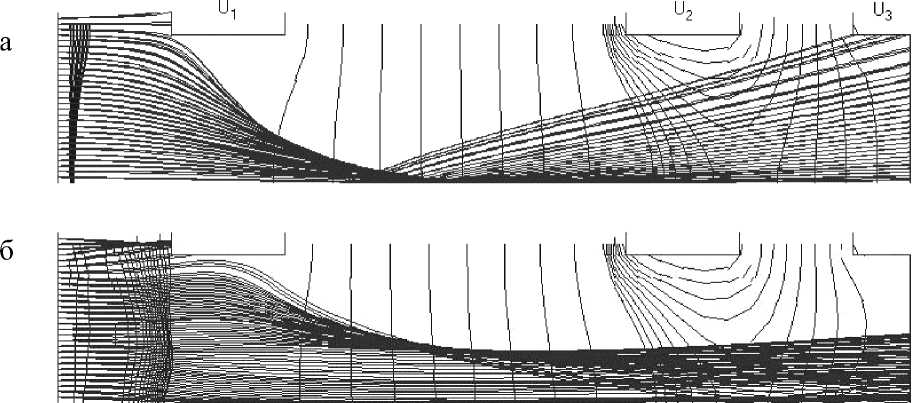
Рис. 1. Электродная осесимметричная система источника ионов, эквипотенциали поля и трубки ионного тока для различных значений концентрации плазмы:

без учета объемного заряда (а), n i = n e = 7.5 х 10 ¹⁰ см^-3 (б), n i ~ n e = 1.5 х 10 ¹¹ см^-3 (в), n i ⁼ n e = 3.0 х 10 ¹¹ см^-3 (г). Приведена верхняя половина системы

40–50 ньютоновских итераций. При относительной точности 10 - 3 требовалось всего несколько итераций.

Разработанная вычислительная процедура, алгоритмы и программа в настоящей работе используются для моделирования источников с экстракцией ионов из плазмы. Такие системы используются для формирования интенсивных ионных пучков [2]. Схема источника изображена на рис. 1. Он состоит из трех осесимметричных электродов, к которым приложены потенциалы U ₁ = 40 000 В, U 2 = 0 и U 3 = 4000 В.

ИНТЕРПРЕТАЦИЯ РЕЗУЛЬТАТОВ КОМПЬЮТЕРНЫХ ЭКСПЕРИМЕНТОВ

Область слева от первого электрода — область плазмы. Эта область является наиболее "тяжелой" в вычислительном отношении. Концентрации ионов и электронов здесь приблизительно одинаковы, и в правой части уравнения Пуассона (2) стоит разность двух больших и приблизительно равных величин. Поэтому в большинстве имеющихся алгоритмов моделирование движения ионов начинается с границы плазмы, которая определяется вне вычислительной процедуры исходя из некоторых модельных представлений. Используемая в настоящей работе вычислительная методика позволила моделировать движение ионов как в области плазмы, так и вне ее. Граница плазмы в этой методике получается автоматически как переходная область от области с практически постоянным потенциалом и высокой концентрацией электронов, равной кон- центрации ионов, к области с убывающим потенциалом и превалирующим ионным объемным зарядом. Это обстоятельство крайне важно, поскольку положение и форма границы плазмы определяют параметры формируемого ионного пучка [2].

Результаты моделирования представлены на рис. 1. Здесь изображены электроды, эквипотен-циали поля и трубки ионного тока для различных значений плотности плазмы и соответственно для различных значений плотности ионного тока. Рис. 1, а дает картину траекторий пучка без учета объемного заряда — это первая итерация решения уравнения Власова. Пучок имеет широкую угловую расходимость. Последующие рисунки представляют результаты, когда итерационный процесс сошелся с заданной точностью по распределению поля и объемного заряда. Учет объемного заряда приводит к кардинальным изменениям в структуре поля в области первого электрода и в форме пучка. Сгущение эквипотенциалей поля в области первого электрода (здесь они проведены с шагом 5 В) следует трактовать как границу плазмы. Ее размеры составляют несколько радиусов Дебая, значения которого для рассматриваемых плотностей плазмы составляют 6 x 10 - 3 см (рис. 1, б ), 4 x 10 - 3 см (рис. 1, в ) и 3 x 10 - 3 см (рис. 1, г ). Распределение потенциала поля на оси для случая n i ~ n e = 3.0 x 10 ¹¹ см^-3 представлено на рис. 2 (кривая 1): в области границы плазмы начинается падение потенциала поля. Здесь же для сравнения представлено распределение лапласова (без учета объемного заряда) поля.

С увеличением плотности плазмы происходит

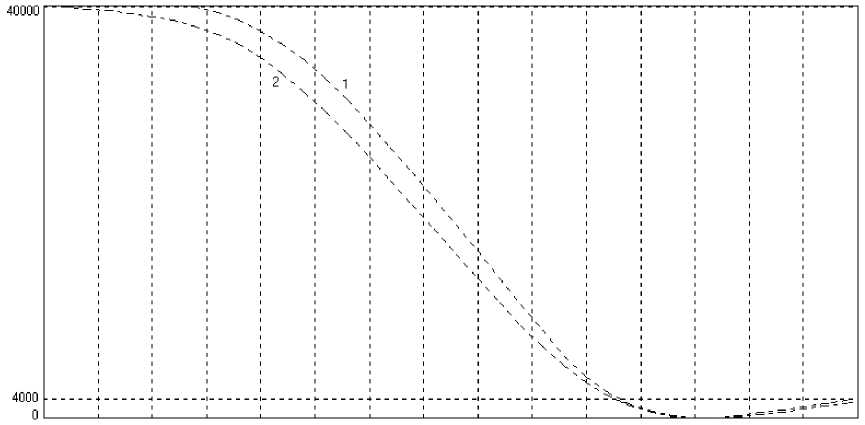
Рис. 2. Распределение поля на оси системы для случаев: 1 — n i = n e = 3.0 x 10 ¹¹ см^-3 , 2 — без учета объемного заряда

сдвиг границы плазмы вниз по пучку (рис. 1, б, в, г ), что соответствует основным экспериментально наблюдаемым закономерностям извлечения ионов из плазмы [2].

ЗАКЛЮЧЕНИЕ

Разработанная вычислительная процедура обеспечивает сходимость процесса за 20–70 итераций по ионному объемному заряду (внешние итерации). При этом требуется несколько десятков итераций метода SOR. Все это обеспечивает приемлемое время счета (доли минуты на один цикл итераций) на персональных компьютерах среднего уровня.