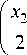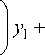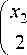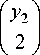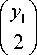Компьютерное моделирование конечных двупорожденных групп периода 5

Пусть B ₀ (2, 5, k ) – максимальная конечная двупо-рожденная бернсайдова группа периода 5 ступени нильпотентности k . В данном классе групп наибольшей является группа B ₀(2, 5,12) , порядок которой равен 5³⁴ [1]. Положим, что { a ₁, a ₂} – порождающие элементы B ₀(2,5, k ) .

Авторами вычислены функции роста указанных групп для порождающего множества A = { a 1 , a - ¹, a 2 , a 21 } при к <  5 . Функция роста группы B ₀ (2, 5,6) относительно А получена Ч. Симсом в работе [2].

На множестве А введем отношение порядка ≺ (меньше): a 1 ^ a -1 ^ a 2 ^ a 21 .

Для получения функции роста и диаметра Кэли относительно А необходимо перечислить все элементы группы в формате минимальных слов [2], а после определения количества слов на каждой длине можно будет найти функцию роста группы, при этом максимально возможная длина минимальных слов будет являться диаметром Кэли группы.

Отметим, что для случаев k = 2, 3, 4, 5 были использованы компьютерные вычисления, основанные на алгоритме перечисления элементов группы.

Алгоритм перечисления элементов группы. Пусть p – простое число, а G – конечная группа экспоненты p . Это значит, что g^p = 1 для всех g е G . Так как группа G нильпотентна, то мы можем найти цепочку подгрупп G i (1 <  i <  n ), обладающих следующими свойствами:

• -    G = G о G ₂ о.о G n о G_n +i = e ;

• -    G i нормальны в G ;

• -    факторы G i / G_{i + 1} имеют порядок p и лежат в центре G / G_{i + 1} .

Пусть для 1 < i < n элемент ai е Gi, но ai е Gi+1. Тогда каждый элемент группы g е G однозначным образом записывается в виде g = a/1 a 22 ann, 0

Такое представление элементов группы (pc-представление) можно получить при помощи алгоритма, известного как P-Quotient Algorithm [3]. Он реализован в системах компьютерной алгебры GAP и Magma.

Если А – порождающее множество группы G, то любой ее элемент, записанный в виде слова a1 a2 ... as, где ai е A , можно преобразовать к виду (1):

pq a1 a2... as ^ a/1 a22. ann. (2)

Процедура (2) дает возможность решить проблему равенства слов в G. На ее основе мы можем перечислить элементы G в формате минимальных слов.

Обозначим через K_s (G) множество всех минимальных слов группы G, не превосходящих по длине s, через множество Q_s (G)– элементы K_s (G), записанные в виде правой части (2), через e – пустое слово – единицу группы.

Пусть s₀е N - минимальное число, для которого выполняется равенство Ks0(G) = Ks0 ₊₁(G). В этом случае s₀ будет являться диаметром Кэли группы G. Опишем алгоритм, вычисляющий K_s .

Шаг 1: s = 0, Kо = {e}, Qo = {e}, T = Kо.

Шаг 2: s = s +1, K_s = K_s-1, Q_s = Q_s-1, V = xT u yT , T = 0 , i = 1.

Шаг 3. Для vi е V v? = f (vi). Если v е Qs, то Ks = Ks u vi, Qs = Qs u v, T = T u vi.

Шаг 4. Если i < | V|, то i = i +1 и переход на шаг 3; если i = | V |, то переход на шаг 5.

Шаг 5. Если T ^ 0, то переход на шаг 2; если T = 0, то переход на шаг 6.

Шаг 6. Если диаметр G равен s -1, то тогда K_s-1(G) - множество всех минимальных слов группы.

Шаг 7. Завершение работы алгоритма.

Работа выполнена при финансовой поддержке КГАУ «Красноярский краевой фонд науки и научно-технической дея- тельности».

Таблица 1

Таблица 2

Таблица 3

Таблица 4

Таблица 5

Таблица 6

Группа B₀(2,5,1). Данная группа представляет собой элементарную абелеву группу, порядок которой равен 5² . Нетрудно вычислить функцию роста данной группы и диаметр Кэли (табл. 1). Справедлива следующая теорема.

Теорема 1. Относительно порождающего множества А группа B₀(2,5,1) имеет диаметр Кэли, равный 4, а функция ее роста задана табл. 1.

Доказательство теоремы очевидно.

Группа B₀(2, 5, 2). Любой элемент группы B₀ (2, 5, 2) может быть представлен в виде нормального коммутаторного слова [1]:

g = a^¹ a22 a3³, уi e Z5.

-14  -14

Здесь и далее a1 = a1 и a2 = a2 .

Для умножения элементов будем использовать полиномы Холла, полученные в [4].

Пусть a1x1a2x2 a3x3 и a1y1a2y2a3y3 – два произвольных элемента в группе B0(2, 5, 2) , записанных в коммутаторном виде. Тогда их произведение a1x1 a2x2 a3x3 ∙ a1y1 a2y2 a3y3 = a1z1 a2z2 a3z3 , где zi e Z5, и zi = xi + У1, z 2 = x 2 + y 2, z 3 = x3 + У 3 + x 2 Ур

Применив алгоритм перечисления элементов группы, получим функцию роста группы B₀(2,5,2) (табл. 2).

Имеет место следующая теорема.

Теорема 2. Относительно порождающего множества А группа B₀(2,5,2) имеет диаметр Кэли, равный 6, а функция ее роста задана табл. 2.

Доказательство теоремы следует из вычислений функции роста группы B₀(2,5,2) по алгоритму перечисления элементов группы.

Группа B0(2,5,3). Каждый элемент группы B0(2,5,3) может быть представлен в виде нормального коммутаторного слова g = a^1 a22 a33 a44 a55, уi e Z5.

Пусть a₁^x1a₂^x2a₃^x3a₄^x4a₅^x5 и a₁^y1a₂^y2a₃^y3a₄^y4a₅^y5– два

произвольных элемента в группе B₀(2,5,3) , записанных в коммутаторном виде. Тогда их произведение

a₁^x1a₂^x2a₃^x3a₄^x4a₅^x5∙ a₁^y1a₂^y2a₃^y3a₄^y4a₅^y5 =

= a1z1a2z2a3z3a4z4a5z5, где zi e Z5, и

zi = xi + У1,

^z 2 = x 2 + y 2 ,

^z 3 = x 3 + y 3 + x 2 У1,

z₄

= x4 + y 4 + x₂

y?¹1 + x3 У1,

I x 2 I z 5 = x5 + У 5 + x 2 У1У 2 +1 2 I У1 + x3 У 2 .

I n

Здесь и далее

I r

n!

!(n - r)!

– биномиальный

коэффициент.

Используя алгоритм перечисления элементов группы, вычислим функцию роста группы B₀(2,5,3) (табл. 3).

Справедлива следующая теорема.

Теорема 3. Относительно порождающего множества А группа B₀(2,5,3) имеет диаметр Кэли, равный 10, а функция ее роста задана табл. 3.

Доказательство теоремы следует из вычислений функции роста группы B₀(2,5,3) по алгоритму пере-

числения элементов группы.

Группа B₀ (2,5,4). Каждый элемент группы B₀ (2, 5, 4) может быть представлен в виде нормального коммутаторного слова:

g = a''a22a^³a44a 15a 16a77as⁸, Yi e Z5•

I У' L I У' L z6 = ^X6 ⁺У6 ^{+ X}2 I з I^{+ X}3 I 2 I ^{+ X}4У1,

z₇

X7 + У₇+

y₁

+

Пусть a₁^x1 a₂^x2 a₃^x3 a₄^x4 a₅^x5 a₆^x6 a₇^x7 a₈^x8 и a₁^y1 a₂^y2 a₃^y3 a₄^y4 a₅^y5 a₆^y6 a₇^y7 a₈^y8 – два произвольных элемента в группе B₀ (2, 5, 4) , записанных в коммутаторном виде. Тогда их произведение

I У' I

^{+ X} 2 I 2 I У 2 ^{+ X} 3 У1У 2 ^{+ X}4 У 2 ^{+ X}5 У1,

z₈

= X 8 + У 8 + x2

У1У 2 ⁺

a₁^x1a₂^x2a₃^x3a₄^x4a₅^x5a₆^x6a₇^x7a₈^x8∙ a₁^y1 a₂^y2 a₃^y3 a₄^y4 a₅^y5 a₆^y6 a₇^y7 a₈^y8 = = a₁^z1a₂^z2a₃^z3a₄^z4a₅^z5a₆^z6a₇^z7a₈^z8,

^{+ X} 2 У1

+ X₃

IУ 2 I

I 2 J

^{+ X}5 У 2,

где zi e Z5, и

zi = ^Xi + У1, ^z 2 = ^X 2 + y 2 , z3 = x3 + y3 + x2 у' ,

z₄

x4 + у₄+ x₂

^{+ x}3 У1,

I x 2 I

^z 5 = ^X5 ⁺У 5 ^{+ X} 2 У1У 2 ⁺ I 2 I У1 ^{+ X} 3 У 2,

Применив алгоритм перечисления элементов группы, найдем функцию роста группы B₀(2,5,4) (табл. 4).

Имеет место следующая теорема.

Теорема 4. Относительно порождающего множества А группа B₀ (2, 5, 4) имеет диаметр Кэли, равный 19, а функция ее роста задана табл. 4.

Доказательство теоремы следует из вычислений функции роста группы B₀(2,5,4) по алгоритму пере-

числения элементов группы.

Группа B₀(2,5,5). Аналогичным образом вычислим функцию роста группы B₀(2,5,5) (табл. 5).

Справедлива следующая теорема.

Теорема 5. В алфавите А группа B₀(2,5,5) имеет диаметр Кэли, равный 20, а функция ее роста задана табл. 5.

Доказательство теоремы следует из вычислений функции роста группы B₀(2,5,5) по алгоритму перечисления элементов группы.

Группа  B₀ (2,5,6). Функция роста группы

B₀(2,5,6) вычислена в работе [2] (табл. 6).