Компьютерное моделирование нагрузки на голень методом конечных элементов

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 620.179.1:616                                 

Остеоартроз (ОА) коленного сустава является распространенным и инвалидизирующим заболеванием опорно-двигательного аппарата, поражающим миллионы людей по всему миру, что представляет собой существенное бремя для населения [1].

Постепенное ухудшение состояния суставного хряща, сопровождающийся болью, тугоподвижностью суставов и функциональными ограничениями, отрицательно влияет на качество жизни и увеличивает расходы на здравоохранение [2].

Ожидаемый рост заболеваемости ОА коленного сустава требует эффективных и экономически целесообразных стратегий лечения.

Компьютерное моделирование в медицине в последнее время активно развивается и является современной методикой исследования. Одним из методов компьютерного моделирования считается Метод конечных элементов (FEM), первоначально использовавшийся в гражданском строительстве с начала 1940-х годов. На современном этапе развития медицинской науки Метод конечных элементов используется во многих областях медицины [3-5].

Вычислительные технологии с годами усовершенствуются, и в результате можно анализировать более сложные проблемы, связанные с разными органами человека.

Материал и методы

Метод конечных элементов (МКЭ) был впервые представлен в области ортопедической биомеханики в начале 1970-х годов для оценки напряжений в костях человека. К началу 1980-х годов этот метод хорошо зарекомендовал себя как инструмент для фундаментальных исследований и анализа дизайна. С конца 1980-х и начала 1990-х годов МКЭ также использовался для изучения ремоделирования кости. Сегодня это один из самых надежных инструментов моделирования для оценки износа, усталости, распространения трещин и т. д., и он используется во многих типах предоперационных испытаний. С момента внедрения FEM в ортопедическую биомеханику произошел быстрый прогресс в скорости компьютерной обработки, конечных элементах и других численных методах, понимании механических свойств мягких и твердых тканей и их моделировании, а также в методах обработки изображений. В свете этих достижений сегодня принято, что МКЭ будет продолжать вносить значительный вклад в дальнейший прогресс в дизайне и разработке ортопедических имплантатов, а также в понимании других сложных систем человеческого тела. Основные области применения конечно-элементного моделирования в ортопедии, включая эндопротезирование крупных суставов таких как тазобедренный, коленный и голеностопный суставы соответственно.

Метод конечных элементов

Основная идея метода конечных элементов состоит в том, что любую непрерывную величину, такую как температура, давление и перемещение, можно аппроксимировать дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей. Кусочно-непрерывные функции определяются с помощью значений непрерывной величины в конечном числе точек рассматриваемой области. В общем случае непрерывная величина заранее неизвестна, и нужно определить значения этой величины в некоторых внутренних точках этой области. Дискретную модель, однако, очень легко построить, если сначала предположить, что числовые значения этой величины в каждой внутренней точке области известны. После этого можно перейти к общему случаю. Итак, при построении дискретной модели непрерывной величины поступают следующим образом:

• 1.    В рассматриваемой области фиксируется конечное число точек, называемых узловыми точками или просто узлами.

• 2.    Значение непрерывной величины в каждой узловой точке считается переменной, которая должна быть определена.

• 3.    Область определения непрерывной величины разбивается на конечное число подобластей, называемых элементами. Эти элементы имеют общие узловые точки и в совокупности аппроксимируют форму области определения.

• 4.    Непрерывная величина аппроксимируется на каждом элементе полиномом, который определяется с помощью узловых значений этой величины. Для каждого элемента определяется свой полином, который подбирается таким образом, чтобы сохранялась непрерывность величины вдоль границ элемента.

Кусочно-непрерывные зависимости отдельного элемента аппроксимируют искомую величину на каждом отдельном элементе, а вместе они аппроксимируют искомую величину на всей рассматриваемой области. Важным условием для кусочно-непрерывной аппроксимации является условие непрерывности переменной и ее производных на границах каждого сочленения элементов. Если непрерывность самой величины достигается автоматически путем использования одних и тех же узловых точек на границах сочленяющихся элементов, то непрерывность производных требует применения определенных дополнительных процедур. Вопрос этот решается при построении дискретной модели в зависимости от определенных условий и целей при решении конкретной задачи.

Узловые значения искомой величины неизвестны и являются целью при решении уравнений. Они должны быть отрегулированы таким образом, чтобы обеспечить наилучшее приближение к истинному распределению искомой величины. Эта цель достигается путем минимизации (максимизации) некоторого функционала, связанного с физической сущностью задачи. Процесс минимизации функционала приводит к построению системы линейных алгебраических уравнений относительно узловых значений аппроксимирующих величин. В процессе решения системы уравнений определяются узловые значения искомой величины, обладающие свойством наилучшего приближения к истинным значениям.

Несмотря на универсальный характер метода, он имеет свои характеристики, которые не безграничны. Положительными характеристиками данного метода являются:

• 1.    Свойства материалов смежных элементов могут быть отличными друг от друга. Это позволяет применять метод к средам с изменяющимися в пространстве свойствами, что важно для областей знаний использующих или изучающих среды с неоднородными свойствами материала.

• 2.    Любая криволинейная область может быть аппроксимирована линейными элементами, что также очень важно для приложений в различных областях знания, рассматривающих самые различные формы.

• 3.    Размеры каждого отдельного элемента могут быть совершенно различны, что позволяет сделать сетку элементов более мелкой в важных областях и более крупной в менее важных.

• 4.    Метод позволяет рассматривать разнообразные граничные условия, с разрывной поверхностной нагрузкой, а также смешанные граничных условия.

Моделирование нагрузки на голень

Строение костей голени. На Рисунке 1 показано строение костей голени. Изучаемый объект представляет собой спаренные две кости — большеберцовую и малоберцовую. Для целей лечения по определенной методике, при которой удаляется часть малоберцовой кости, необходимо было изучить, каким образом данная методика лечения отразится на функциональном состоянии и возможностях большеберцовой кости. Для построения модели определения напряженного состояния, возникающего в большеберцовой кости при очевидной нагрузке, связанной с весом тела человека, была использована методика математического расчета упругих смещений, возникающих под воздействием веса человека. Ниже приведена геометрическая модель костей голени человека. Она является упрощением представления реальных большеберцовой и малоберцовой костей, но отражает все основные особенности функционирования под нагрузкой этого элемента костной системы человека. Тем более, что двух одинаковых голеней, полностью повторяющих друг друга по форме и строению у двух разных людей, не бывает, в связи с половыми, возрастными и прочими особенностями разных людей.

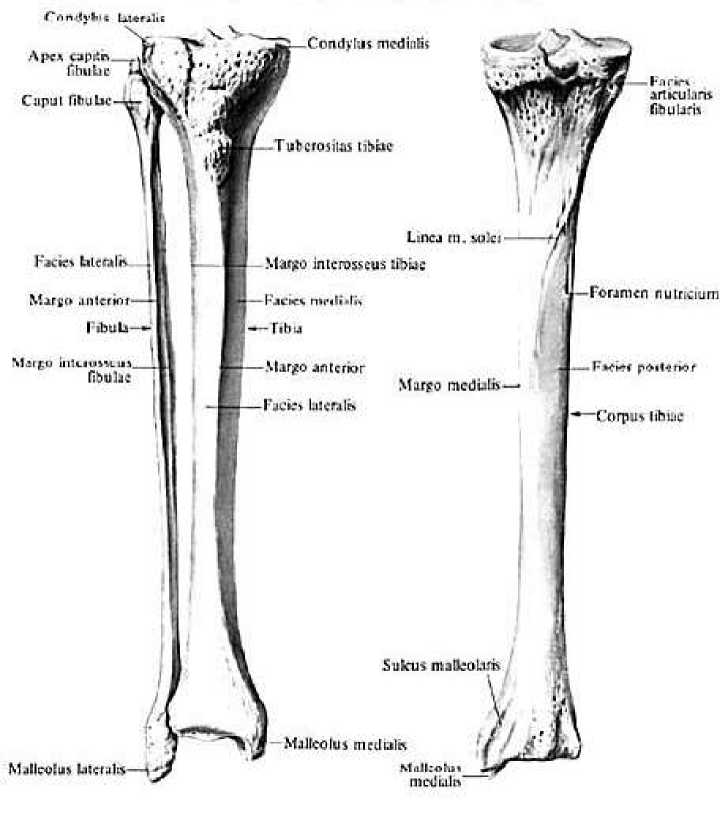
Рисунок 1. Строение костей голени

Общая высота модели костей голени составила 40 см. Ширина верхнего и нижнего оснований составила по 5 см. Ширина большеберцовой кости составила 3 см, малоберцовой — 1 см. Расстояние между берцовыми костями составило 1 см. Расстояние от основания до начала промежутка между костями составило 2 см. Данная геометрическая модель голени не учитывает сложный характер строения костей и подробную геометрию конкретной кости человека, но отражает общие особенности строения голени. Модель также представляет собой двумерную модель, как бы поперечный разрез голени человека.

Данная методика вполне достаточна для достижения целей, связанных с выяснением перераспределения нагрузок на кости голени, вызванных оперативным вмешательством.

Трехмерная модель голени была бы, конечно предпочтительней, однако все необходимые результаты возможно получить и с двумерной моделью голени, что подтвердили полученные результаты, о которых будет идти речь ниже (Рисунок 2).

Таким образом, расчет проводился с целью выяснения изменения распределения нагрузок и смещений, происходящих в голени человека при оперативном вмешательстве, а именно: удалении части малоберцовой кости для коррекции нагрузок вызванных патологическими изменениями в коленном суставе. Для этих целей были проведены две серии расчетов. Первая — расчеты распределения напряжений и смещений при обычном состоянии и целостности обеих берцовых костей. Вторая серия расчетов была проделана для случая, когда малоберцовая кость отсутствует. Этот случай моделирует удаление части малой берцовой кости, что фактически означает ее отсутствие и неучастие в распределении нагрузок, которые несет голень под воздействием веса человека.

На Рисунке 3 приведены геометрических модели представления голени для указанных двух случаев. Модель под номером 1) относится к первому случаю, а модель под номером 2) — ко второму случаю.

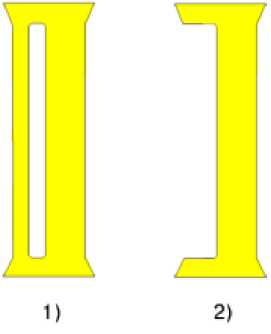
Рисунок 2 Модель голени человека,       Рисунок 3 Геометрические модели голени использованная для проведения расчетов         для двух случаев

Верхняя поверхность голени соприкасается с бедренной костью, а нижняя часть – опирается на кости стопы. Для обоих случаев нагрузка представлялась одной и той же и составляла 1.6 МПа, что моделирует вес человека примерно в 50 кг на одну голень. Собственный вес голени не принимался в расчет. Упругие свойства кости, необходимых для проведения исследования, были взяты из источников и составляли: модуль упругости – 104 МПа, коэффициент Пуассона – 0.3.

Таким образом, верхняя поверхность голени представляла собой площадку с вертикальным давлением в 1.6 МПа. Все боковые поверхности представляли собой граничные условия с нулевой нагрузкой. Наконец нижняя поверхность, соединяющаяся со стопой, представляла собой поверхность с нулевыми смещениями. Расчеты проводились с помощью программы [4] методом конечных элементов в двумерной постановке.

Результаты и их обсуждение

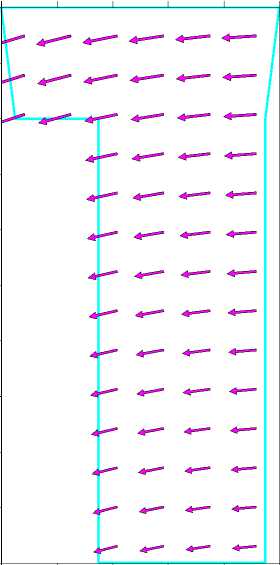
В результате проведенных расчетов модели голени были получены поля распределений напряжений и векторов смещений. Вектора смещений показывают результирующие силы, которые действуют в указанной точке объема берцовой кости. Напряжения выражены в мегапаскалях, смещения в миллиметрах. На Рисунках 4, 5 показаны верхние части модели большеберцовой кости, поскольку именно в этой части ярко проявляются необходимые нам результаты.

На Рисунке 4 приведены результирующие упругие смещения для случая 1, когда обе берцовые кости участвуют в распределении нагрузки, т.е. являются целыми. На рисунке 5 показаны результирующие упругие смещения для случая 2, когда в результате оперативного вмешательства удалена малоберцовая кость и она не участвует в принятии весовой нагрузки тела человека.

0.3

0.4

0.39

0.38

0.37

0.36

0.35

0.34

0.33

0.32

0.31