Компьютерное моделирование процесса функционирования автореверсивной втулки из материала с памятью формы

изготовления ответственных деталей и узлов, входящих в состав бортовых систем, является актуальной проблемой совершенствования производства современных летательных аппаратов.

Производственные задачи данного класса могут быть решены за счет применения материала с эффектом памяти формы (ЭПФ) в конструкции технологического оснащения, предназначенного для выполнения операций прецизионного шлифования, операций прецизионной стыковки перед сваркой, операций сборки пластическим деформированием и т.п. Рабочей частью технологического оснащения для выполнения подобных операций является втулка, изготовленная из сплава, обладающего ЭПФ (например, TiNi ). После соответствующей предварительной подготовки, на раздачу или на обжим, такая втулка способна соответственно уменьшаться или увеличиваться в диаметре при нагреве и увеличиваться или уменьшаться в диаметре при охлаждении. Иными словами, втулка из сплава с ЭПФ, после предварительной подготовки радиально деформируется при фазовом переходе ее материала в результате нагрева или охлаждения. Свойства сплавов с ЭПФ позволяют обеспечить требуемую цикловую стабильность и осесимметричность радиальных перемещений рабочей поверхности данной втулки [1, 2].

Для успешного внедрения в производство технологических процессов рассматриваемого класса необходима инженерная методика проектирования соответствующего технологического оснащения. Необходимая методика проектирования данного технологического оснащения может быть разработана с применением аналитических зависимостей связывающих конструктивные параметры и параметры подготовки рабочей части оснащения с параметрами ее функционирования.

Эта цель может быть достигнута за счет решения задачи по аналитическому моделированию процесса функционирования силового элемента в виде втулки из сплава с ЭПФ и сравнения полученных ранее соответствующих результатов [3].

Для подтверждения адекватности результатов аналитического моделирования проведено компьютерное моделирование процесса функционирования рабочей части оснащения (втулки из материала с ЭПФ) с использованием системы ANSYS. К тому же, компьютерное моделирование процесса подготовки и функционирования втулки из материала с ЭПФ позволяет глубже исследовать процессы, происходящие в материале, которые влияют на работоспособность технологического оснащения.

ПРОВЕРКА КОРРЕКТНОСТИ ПАРАМЕТРОВ МАТЕРИАЛА С ЭПФ

На первом этапе компьютерного моделирования процесса работы втулки проведено математическое описание свойств материала с памятью формы. Для описания поведения материала была использована трехмерная термо- механическая конечно элементная модель для фазовых превращений под действием напряжений, описанная в [4]. В рамках классической необратимой термодинамики, используемая модель способна воспроизводить все основные особенности поведения материалов с памятью формы в объемном напряженно-деформируе- мом состоянии.

В основе используемой модели лежит известное уравнение потенциала свободной энер- гии, которое имеет вид:

V⁽£, Т, s_tr) = | (£ - e_try.D\(E- s_tr) +

+ T _M ⁽ T ⁾lktrll + ^Ms trlP "^ Is'tr^tr^ ,

где D - тензор упругой жесткости материала;

ε – общая деформация;

б _tr - общая деформация фазового перехода;

б у - девиаторная деформация фазового перехода;

tM(T) - положительная и монотонно возрас тающая функция температуры в(Т-Т0);

β – параметр материала, характеризующий величину деформации памяти формы;

Т – текущая температура;

Т ₀ - температура конца мартенситного перехода в ненапряженном состоянии;

h - параметр материала, связанный с упрочнением материала во время фазового перехода;

l e^^tr ) - индикаторная функция, введенная для соблюдения условий нормирования деформации перехода.

Для проверки корректности параметров материала с ЭПФ, используемых в конечно - элементной модели, создаваемой в системе ANSYS, были проведены сравнительные тестовые эксперименты. Для этого была рассмотрена одномерная задача, описывающая функционирование проволоки из материала с ЭПФ. Проведены натурные эксперименты, заключающиеся в термоциклировании проволоки из материала с ЭПФ, а также выполнены численные эксперименты по исследованию этого процесса с помощью программы ANSYS. Целью сравнения экспериментальных результатов натурного моделирования с результатами численного эксперимента был подбор библиотечных характеристик материала с ЭПФ, содержащихся в системе, для использования их при моделировании процесса функционирования автореверсивной втулки.

Для тестового эксперимента была использована проволока из сплава ТН-1 длиной 400 мм и диаметром 1 мм. Один конец проволоки был закреплен. Для задания равномерных по длине проволоки деформаций наведения был применен технологический прием - проволока нагревалась до температуры выше температуры конца обратного мартенситного превращения ее материала (400 °С) путем пропускания по ее сечению электрического тока. Далее противоположный конец проволоки нагружался силой в 300 Н путем закрепления соответствующих грузов на свободном конце. Нагрев отключался, и материал проволоки охлаждался до температуры ниже температуры конца прямого мартенситного превращения (22 °С). В процессе охлаждения проволока растягивалась – в ее материале создавалась деформация наведения. Далее грузы частично убирались, и соответствующая нагрузка (нагрузка сопротивления) составляла 100 Н. Потом проволока аналогичным образом нагревалась до температуры выше температуры конца обратного мартенситного превращения ее материала (400 °С). В результате проволока сокращала свою длину. Температура нагрева контролировалась термопарой и потенциометром. На каждом этапе эксперимента длина проволоки контролировалась с помощью рулетки. В результате эксперимента установлено, что после деформирования с нагрузкой 300Н длина проволоки увеличилась на 48±0,5 мм. При уменьшении нагрузки до 100Н удлинение образца составило 44±0,5 мм при напряжении сопротивления 127 МПа. После нагрева материала проволоки до 400 °С удлинение проволоки составило 17±0,5 мм при неизменившемся напряжении сопротивления.

Далее данная задача функционирования проволоки из материала с ЭПФ была смоделирована в системе ANSYS. Для конечно элементной модели был выбран балочный элемент BEAM188. Задана длина элемента - 1,5 мм и его диаметр – 1,0 мм. Свойства материала с ЭПФ заданы в библиотеке системы ANSYS Shape Memory Alloy с различными значениями соответствующих параметров. В результате моделирования процесса наведения деформации памяти формы и процесса возврата при термоупругих фазовых превращениях, получены численные решения данной задачи для различных значений библиотечных параметров. Из множества полученных решений выбрано то, у которого результаты наиболее близки к результатам тестового эксперимента.

Результаты выбранного решения: на конец первого шага расчета упругопластическое удлинение проволоки составило 46,3 мм, на конец второго шага расчета удлинение составило 42,6 мм, на третьем шаге, при термоупругих фазовых превращениях с действующим напряжением сопротивления 127 МПа, остаточное удлинение равнялось 17,3 мм.

По результатам сравнительного эксперимента натурного и численного моделирования проведен уточненный выбор параметров материала с ЭПФ.

В дальнейшем данная модель материала с уточненными коэффициентами была применена при моделировании процесса функционирования рабочего элемента приспособления - втулки из материала с ЭПФ.

МОДЕЛИРОВАНИЕ ПРОЦЕССА ФУНКЦИОНИРОВАНИЯ ВТУЛКИ ИЗ МАТЕРИАЛА С ЭПФ

Цель моделирования состояла в определении напряженно-деформированного состояния втулки из материала с ЭПФ, особенно распределения окружных напряжений вдоль радиуса втулки. Это важно для научного подтверждения существования эффекта автореверсивности рабочего элемента приспособления, обеспечивающего его стабильное и многоцикловое функционирование.

Численное моделирование производилось с применением статического анализа в плоской осесимметричной постановке. Применен конечный элемент PLANE182. Наружный диаметр втулки задан равным 28 мм (точка 2), диаметр осевого отверстия задан равным 14 мм (точка 1). Длина втулки 30 мм (рисунок 1).

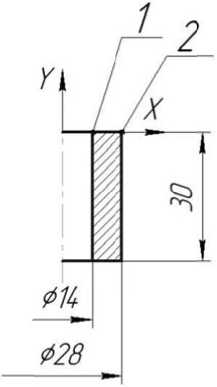
Рис. 1. Расчетная схема для моделирования процесса функционирования втулки

Задача решалась в 3 этапа.

На первом этапе в материале втулки создавалось поле деформаций наведения за счет перемещения поверхности отверстия вдоль оси Х. На практике такое поле деформаций наведения в материале втулки выполняется, например, путем дорнования.

На втором этапе перемещения поверхности отверстия снимались, то есть освобождалась поверхность внутреннего отверстия (например, путем извлечения дорна), и происходил упругий возврат втулки.

На третьем этапе задавался равномерный по сечению нагрев втулки от начальной температуры 22°С до конечной температуры 400 °С (выше температуры конца обратного мартенситного превращения материала втулки). На этом этапе моделировался процесс возврата втулки к форме, приближенной к первоначальной, другими словами диаметры внутреннего отверстия и наружной поверхности уменьшались.

Для разработанной конечно-элементной модели задавались последовательно четыре значения перемещения наведения: 0,10; 0,15; 0,20 и 0,25 мм на радиус внутреннего отверстия.

Результатами моделирования являются значения компонент, характеризующих напряженно-деформированное состояние втулки из материала с ЭПФ (радиальные напряжения, окружные напряжения, радиальные деформации, окружные деформации) для решений на всех этапах численного эксперимента в точках, расположенных вдоль оси Х (от точки 1 до точки 2 на рис. 1).

Получены также зависимости изменения окружных напряжений (на этапе возврата) от раздачи втулки (рис. 2, рис. 3).

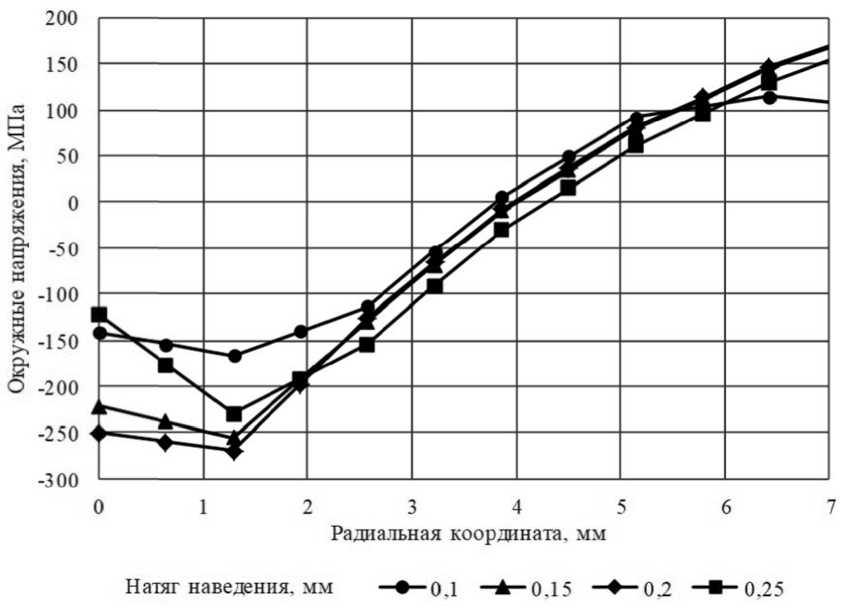
Рис. 2. Распределение окружных напряжений в зависимости от раздачи втулки (по толщине втулки) при различных натягах наведения

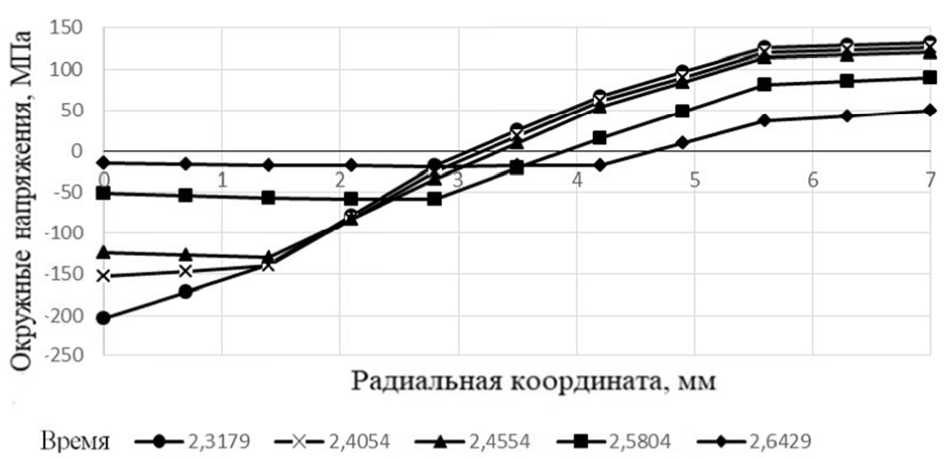
Рис. 3. Распределение окружных напряжений по толщине втулки на этапе возврата

ВЫВОДЫ

Полученная модель позволила оценить поведение втулки из материала с ЭПФ в различных условиях. При этом было определено напряженно-деформированное состояние исследуемого объекта (радиальные напряжения, окружные напряжения, радиальные деформации, окружные деформации) и его влияние на работоспособность технологического оснащения.

Кроме того, был произведен численный эксперимент при разных значениях перемещения наведения на радиус внутреннего отверстия, который показал зависимость тангенциальных напряжений от величины натяга наведения.

Таким образом, полученные результаты хорошо согласуются с аналитическим моделированием, и указывают направление проведения натурного эксперимента.