Компьютерное моделирование процессов накопления повреждений в твердых телах с трещинами с помощью пользовательской процедуры UMAT вычислительного комплекса Simulia Abaqus

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2018PNRPU MECHANICS BULLETIN

В настоящее время разрушение (макроскопическое нарушение сплошности тела в результате воздействия на него внешнего окружения) рассматривается с учетом процессов скрытого разрушения. Исследование скрытого разрушения (зарождение и развитие микродефектов, рассеянных по объему тела) осуществляется с помощью методов и теорий механики поврежденности - динамично развивающегося раздела современной механики деформируемого твердого тела, теоретические основы которой заложены Л.М. Качановым и Ю.Н. Работновым [1-3]. В последнее время большой интерес вызывают вопросы компьютерного моделирования деформирования, повреждаемости и разрушения неупругих материалов и конструкций [4–6] и развития численных методов, учитывающих повреждаемость материала конструкции с течением времени, а также описания взаимного влияния эволюции поврежденности и напряженно-деформированного состояния [7–11]. В [7–11] предложена и используется одна из моделей анизотропной поврежденности, экспериментальное подтверждение которой обсуждается в [12–16]. В целом в последнее десятилетие и в самое последнее время вопросам компьютерного моделирования роста трещин и длительного разрушения с использованием различных мер повре-жденности посвящается большое количество работ [17– 20], появились фундаментальные монографии [21-23], а в 2014 г. вышло в свет второе издание основополагающей книги Ю.Н. Работнова «Ползучесть элементов конструкций» [24]. Континуальная механика повреж-денности исходит из того, что изменение со временем механических свойств материалов феноменологически можно интерпретировать как результат накопления повреждений, различных дефектов, микропор, трещин. Когда повреждения достигают опасного уровня, происходит разрушение. Трещинообразование начинается на самых ранних этапах деформации и связано с ростом имеющихся и возникновением новых суб- и микродефектов. В материале всегда имеется большое число различных дефектов, приводящих к высоким местным напряжениям. Уменьшение прочности (свойства тела сопротивляться воздействиям со стороны внешнего окружения) деформируемых твердых тел часто может быть объяснено скрытым разрушением и микродефект-ной структурой тела. Таким образом, поскольку повреждения тела существенно влияют на характер его разрушения, становится очевидным, что и механика разрушения, и механика поврежденности призваны решить главную прикладную задачу об оценке запаса прочности твердого тела.

Поэтому сейчас одной из актуальной задач современной механики деформируемого твердого тела и механики разрушения, в частности, является компьютерное имитационное моделирование процессов нелинейного деформирования и разрушения твердых тел под нагрузкой с учетом процессов накопления рассеянных повреждений. Под поврежденностью понимается относительное сокращение вследствие распределенных внутри образца микродефектов эффективной, несущей нагрузку площа- ди поперечного сечения образца [22]. Деградацию материала можно трактовать как последовательное уменьшение эффективной площади, несущей приложенную нагрузку. Процесс накопления повреждений в твердых телах может быть описан с помощью введений скалярной или тензорной меры поврежденности [1–3, 22].

В простейшем варианте поврежденность можно описать некоторым скаляром, структурным параметром 1 >у> 0 [1]. В начальном состоянии при отсутствии поврежденности у = 1, с течением времени функция у убывает. Функцию у можно интерпретировать как сплошность. Ю.Н. Работнов [2, 3] ввел функцию го> 0, равную нулю в начальном состоянии и единице в момент разрушения, которую можно принять за меру охрупчивания. Функцию го естественно назвать повреж-денностью, и можно считать, что у = 1 -го . Величина го может быть интерпретирована как относительная площадь поперечного сечения, занятая трещинами и вакансиями. Предполагается, что скорость изменения параметра поврежденности ГО зависит от напряжения с и от поврежденности го. Простейшая гипотеза состоит в том, что ГО есть степенная функция отношения с / (1 - го ) . Полученное напряжение с_ист = с / (1 - го ) носит название истинного напряжения. Это отношение может быть истолковано как среднее напряжение на площади поперечного сечения, свободной от трещин. Истинное напряжение вводится в определяющие уравнения, построенные для первой и второй стадий ползучести, чтобы описать третий участок кривой ползучести. Впоследствии концепция истинного напряжения была распространена на упругие и пластические деформации [4–6], что позволило учитывать накопления повреждений в условиях упругого нагружения и пластического течения [4–6, 7–9].

В рамках связанной постановки задачи скалярный параметр поврежденности или компоненты тензора по-врежденности входят в определяющие соотношения материала [22]. Исторически первой явилась математическая модель Качанова–Работнова [1–3]

е = ³ B I ^ e

*j   2 IУ

s ij

У

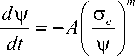
В соотношениях (1) £z?- компоненты тензора скоростей деформаций ползучести; s – девиатор напряжений; у - параметр сплошности; с = ^3SySy / 2 - интенсивность касательных напряжений; B, n, A, — - константы материала. После пионерских работ Л.М. Качанова и Ю.Н. Работнова [1–3] континуальная механика по-врежденности двигалась по пути 1) усложнения определяющих уравнений [4–6], 2) отражения анизотропии, вызванной накоплением повреждений [7–16, 22], 3) решения краевых задач в связках упругость-поврежденность, пластичность-поврежденность и пол- зучесть-поврежденность [25–31]. Существующие модели поврежденности для изотропных материалов были обобщены для анизотропных линейно-упругих материалов (бетон, горные породы), для функциональноградиентных материалов с переменными по координатам свойствами [32], для композиционных материалов [33–42]. Например, позднее определяющие уравнения модели Качанова-Работнова (1) были обобщены и представлены в форме [43, 44]

/ X n -1

е„ = ³ B | — I t^-- ij

2 V У J    У d*=-A 41-.

dt      у^ф

В целом закон роста поврежденности при сложном напряженном состоянии можно установить с помощью экспериментов, в которых находятся комбинации напряжений, приводящие к одному и тому же времени до разрушения. Геометрически такие результаты представляются в виде поверхностей в пространстве напряжений [45]. Математически изохронные поверхности напряжений описывают с помощью некоторого скалярного инварианта напряжений Ф (с₁ , с_е , с^ ) , где с - максимальное главное напряжение; с_е - интенсивность напряжений; с_кк -гидростатическое напряжение. В настоящее время изохронную поверхность чаще всего описывают с помощью следующей линейной интерполяции:

Ф = ^ас , +Р^с _е + ^{(1 -а}-Р ^{) с} kk .

Решение краевых задач механики деформируемого твердого тела для элементов конструкций, находящихся в реальных эксплуатационных условиях, требует использования многофункциональных комплексов, таких как SIMULIA Abaqus. Однако среди моделей материалов, представленных в конечно-элементном пакете SIMULIA Abaqus, нет возможности прямого учета процесса накопления повреждений. Возможность моделирования сложных сред в пакете SIMULIA Abaqus реализуется с помощью пользовательских процедур, таких как UMAT и VUMAT [17, 44, 46].

В настоящей работе представлен опыт использования процедуры UMAT для описания процессов накопления повреждений в образцах с концентраторами напряжений в материале с определяющими уравнениями, базирующимися на конституциональных уравнениях линейно-упругого изотропного материала и включающими компоненты тензора поврежденности второго ранга [7–11]. В работе найдены распределения поврежден-ности у вершины трещины и проанализированы зоны активного накопления повреждений в условиях смешанного нагружения на примере целого ряда задач для тел с различными концентраторами напряжений и разрезами в полном диапазоне смешанных форм нагружения. Выполнена серия вычислительных экспериментов для диска с вертикальной наклонной трещиной (с различными углами наклона надреза к хорде диска) в материале с учетом процессов накопления повреждений.

1. Определяющие уравнения материала с включенными компонентами тензора поврежденности второго ранга

Для учета эффектов анизотропии был предложен целый ряд математических моделей [7–16, 21, 22]. Одна из них – модель для боросиликатного стекла, основанная на введении тензорной меры поврежденности [7– 16]. Определяющие уравнения материала в общем случае имеют вид a,=[Keki(T) + K(T)](ski -sh),          (3)

где a,; - компоненты тензора напряжений; s^ - компоненты тензора деформаций; K^ (T) - компоненты тензора упругих модулей, в общем случае зависящих от температуры; К^и (T) - компоненты тензора упругих модулей, обусловленные накоплением повреждений; sth - температурные деформации. Компоненты тензора упругих модулей K^ (T) вычисляются как классические компоненты тензора упругих модулей линейноупругого изотропного материала

^ = X (T ) 5 , 5 _и + ц ( T )( 5 _а 5 , +5„ 5 у ),       (4)

где X (T ), ц ( T ) - постоянные Ламе. Компоненты тензора упругих модулей K ^ ( T ), обусловленные накоплением повреждений и учитывающие данный процесс, вычисляются с помощью соотношений [7–11]

K k, = C (T )( 5 ^_й +5 „D , ) + C 2 (T)( 5 h D_u + 5 D ), (5)

где D – компоненты тензора поврежденности; C (T), i = 1,2 - константы материала, определяемые экспериментально. Предполагается, что 0 < Dy < 1.

Оригинальная модель анизотропной поврежденно-сти (3)–(5) была предложена для боросиликатного стекла [10] и развита в [11]. Модель анизотропной по-врежденности (3)–(5), как показано в [8], хорошо описывает растрескивание стекла при вдавливании штампа, что подтверждается экспериментальными данными, приведенными в [13, 14]. Подробное изложение экспериментальной процедуры исследования процессов растрескивания и локализации поврежденности приведено в [8]. Уравнения (3)–(5) изначально пред-

ложены для описания процессов деформирования вязкоупругого тела, переходящего в стеклообразное состояние при понижении температуры. В [8–10, 12–14] показано, что модель может быть обобщена на случай произвольного стекла путем выбора параметров модели. Главным преимуществом используемой модели является ее широкое экспериментальное подтверждение для различных классов материалов и условий разрушения [14–16]. Также одним из преимуществ данной модели является ее простота и возможность использования в расчетном комплексе SIMULIA Abaqus, в отличие от моделей, представленных уравнениями (1) и (2), для которых требуется написание достаточно сложной процедуры интегрирования кинетического уравнения по времени. В силу указанной причины находят широкое распространение модели поврежденно-сти с алгебраическими уравнениями, описывающими поврежденность [38, 47]. В целях упрощения математической модели (3)–(5) можно предположить, что недиагональные компоненты тензора поврежденности равны нулю, а нормальные компоненты определяются выражениями

D « =1

^a <^a th ,

^a i ^a th ^{( T} ) a c (T ) -a th ( T ) 1

^a th <^a i <^a c ,

^a , ^ c ,

где a,., i = 1,2,3 - главные напряжения; a_th, a_c - пороговое и критическое значения напряжений соответственно. При напряжениях ниже порогового значения a_th накопления повреждений не происходит. Если главное напряжение a,., i = 1,2,3 достигает критического значения a_c, то материал считается полностью поврежденным, ID = 1. Если поврежденность вызывается касательными напряжениями в плоскости, то компоненты тензора поврежденности вычисляются с помощью соотношений [7, 9, 10]

^Dij =1

^a у <^a th ,

^a у ^-a th ^{( T} )

a c (T ) — a th ( T ) 1

^a th <^a ij <^a c ,

с > с , i,          С ,

В развернутой форме определяющие уравнения материала (3)–(5) принимают вид

a 11		"Х+ 2 ц+ 2 D ,( C + C )
a 22		X + C ( D n + D 22)   Х+ 2 ц+ 2 D 22( C + C )                         SYM		S 22
CT 33		X + C^ ( D^ + D 3 3)    X + C^ ( D 22 + D 3 3)   X + 2 ц + 2 D 3 3( C^ + C 2)		S 33
1	^ = 1		^1
a 12		0                  0                   0            ц		S 12	(8)
a 13		0                  0                   0           0    ц		S 13
_a 23		0                  0                   0           0   0    ц		_S 23

Определяющие соотношения (2)–(8), учитывающие анизотропный характер поврежденности, соответствуют подходу, предложенному для описания процессов накопления поврежденности и разрушения композиционных материалов в [35]. Подробные обзоры современной научной литературы, посвященной проблематике описания процессов накопления поврежденности и разрушения, могут быть найдены в [36–38].

Определение значений материальных констант C и C в уравнениях (3)–(8) представляет собой нетривиальную задачу, требующую выполнения целого ряда экспериментов. Тем не менее для простых случаев можно воспользоваться следующими соображениями. В случае двухосного растяжения квадратной пластины можно принять, что компоненты тензора напряжений g_h и g₂₂ обращаются в нуль, когда D_n = D₂₂ = 1,0, в то время как для плоской задачи справедливо D₃₃ = 0. Для данного нагружения в силу симметрии должно выполняться е_п = б₂₂ = б :

G_n = g₂₂ = 0 = {2( ^ + ^ ) + 2(2 С ₍ + С₂ )} б + { X + С }б_{3 3}, (9)

g₃₃ = 0 = {2( X + С )} б + { X + 2 ц }б_{3 3}.        (10)

Из полученных равенств можно найти значения материальных констант С = 2 ц и С₂ = - 3 ц . В вычислениях, приведенных ниже, используется именно этот выбор констант. В [9] указывается и альтернативный

выбор констант С = ц , С₂ = - 1,5 ц , используемый в оригинальной работе [10], в которой два параметра модели находятся из условия обращения в нуль компоненты g j, когда для одноосного растяжения плоского образца D_n = 1 в направлении оси X j.

В [7] тензорная мера поврежденности применяется для описания разрушения боросиликатного стекла в условиях трехосного растяжения. Согласно уравнениям (6) компоненты тензора поврежденности связываются с главными напряжениями и с направлениями главных осей тензора напряжений. Авторы апеллируют к экспериментальным данным [8] и замечают, что в условиях температурного нагружения, рассматриваемого ими, нагружение является строго пропорциональным и в центральной части цилиндрического образца реализуется трехосное растяжение с главными осями, совпадающими с осями цилиндрической системы координат. Поэтому определяющие уравнения формулируются в цилиндрической системе координат:

g

^G 66

^Б 66

_< ^G zz

^G6 z

^G rz

^G r 6

= A <

^Б zz r ^{2 Б} е z

2б rz

2 б r _e

	Г   X 1 + 2 DrrG	X + С 1 ( D rr + D 66 )	X + С 1 ( D rr + D zz )	0
	X + С 1 ( D rr + D 9 6 )	Xj + 2 D№G	X + С 1 ( D 66 + D zz )	0
A =	X + С 1 ( D rr + D zz ) 0 0 0 V	X + С 1 ( D 66 + Dzz ) 0 0 0	X 1 + 2 DzzG       0 С 2 ( D zz + D 66 ) ц+      , 0           2 00 0 0

0                   0

CAD+

।    2 У, rr_______zzj_

Q               ^C 2 ^{( D}rr ^{+ D} 66 )

Ц        2

где приняты обозначения X, = X + 2 ц , С = С + С .

Постоянные материала определяются из следующих условий. Компоненты тензора напряжений G_{r r}, g_{6 e}, g_zz, g„ _z, G_rz и G_re обращаются в нуль, когда компоненты тензора поврежденности достигают своего критического значения D_rr = 1, D_ee = 1, D^ = 1. В условиях трехосного растяжения б_п = б₂₂ = б_{3 3}. Тогда должны выполняться два условия

G _rr = G₆₆ =g zz = [X + 2 ц + 2 ( С 1 + С ₂ ) ]б + 2 ( X + 2 С 1 ) б = 0, ^G rz =^G r 6 =^G 6 z = ( ц + ^С 2 )^б = 0.

Откуда легко найти значения материальных постоянных: С =-0,5ц, С2 =-ц. Таким образом, выбор зна- чений материальных постоянных представляет собой нетривиальную задачу и должен осуществляться в каждом случае отдельно, исходя из рассматриваемой задачи.

2.    Пользовательская процедураUMAT МКЭ-пакета Simulia Abaqus

В настоящем параграфе будут приведены конечноэлементные решения задач о трещинах в среде с повре-жденностью в связанной постановке (упругость– поврежденность). Определяющие соотношения (3)–(7) описаны в многоцелевом расчетном комплексе Simulia Abaqus с помощью пользовательской процедуры UMAT. Пользовательские процедуры многофункцио- нального расчетного комплекса Simulia Abaqus позволяют ввести в рассмотрение материалы, отсутствующие в стандартном наборе материальных моделей классического пакета Abaqus/CAE. Все конечно-элементные решения получены для определяющих уравнений (3)–(7). Интерес представляет оценка взаимного влияния эволюции напряженно-деформированного состояния в образце и процесса накопления повреждений, в особенности у вершины трещины или надреза. Первой задачей является задача о всестороннем и одноосном растяжении пластины с центральным круговым отверстием в среде с поврежденностью. Затем рассматриваются задачи определения напряженно-деформированного состояния и поврежденности у вершин трещин в условиях нормального отрыва и смешанного нагружения.

• 2.1.    Распределение поврежденности в пластине с центральным круговым отверстием

В качестве первого образца была выбрана пластина с центральным круговым отверстием под действием 1) всестороннего и 2) одноосного растяжения в материале с определяющими уравнениями (3)–(7). На рис. 1 и 2 показаны распределения поврежденности в пластине с круговым вырезом в условиях всестороннего и одноосного растяжения для определяющих уравнений с включенным тензором поврежденности.

Из рис. 1 и 2 видно, что максимальные значения по-врежденности достигаются на контуре кругового выреза в случае всесторонне растягиваемой пластины и в точках кругового отверстия, лежащих на оси ординат. Поскольку распределения поврежденности, полученные в ходе конечно-элементного эксперимента, соответствуют известным экспериментальным результатам [48, 49], рассматриваемая материальная модель была использована для решения более сложных задач, для анализа зон активного накопления повреждений у вершины трещины.

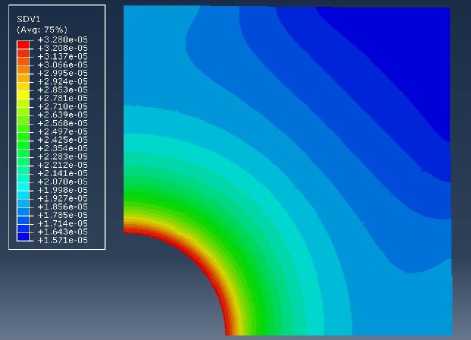
Рис. 1. Распределение компоненты тензора поврежденности D в пластине с центральным круговым отверстием под действием всестороннего растяжения

Fig. 1. Distribution of damage tensor component D in the plate under equi-biaxial tension of the specimen

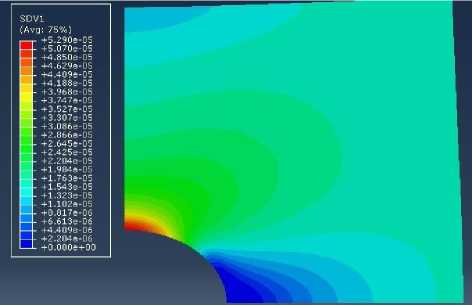
Рис. 2. Распределение компоненты тензора поврежденности D в пластине с центральным круговым отверстием под действием одноосного растяжения по оси x

Fig. 2. Distribution of damage tensor component D in the plate for uniaxial tension of the specimen

• 2.2.    Растяжение пластины с центральной трещиной в среде с поврежденностью

Особый интерес представляет определение конфигурации зон накопления повреждений у вершины трещины. Несмотря на достаточно богатый опыт работы с пользовательскими процедурами пакета SIMULIA Abaqus, накопленный исследователями в нашей стране и за рубежом [17–20, 32, 46, 50, 51], позволяющий моделировать широкий класс материалов с инкорпорированными скалярной и тензорной мерой поврежденности, отсутствуют результаты вычислений, показывающих процессы накопления повреждений вблизи кончика трещины, и их систематичный анализ. В силу указанных причин можно остановиться на простой модели пластины с центральной трещиной. Типичная схема разбиения области, окружающей трещины, показана на рис. 3.

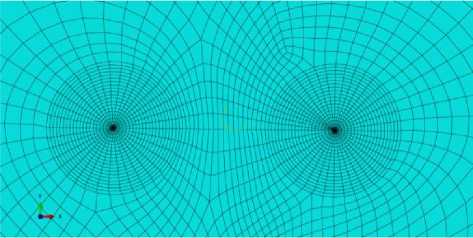
Рис. 3. Пример конечно-элементного разбиения пластины на конечные элементы: вершины трещины окружают сингулярные элементы

Fig. 3. Details of finite element mesh pattern for the simulation the plate with a horizontal central crack and two crack tips with singular elements

Модель анизотропной поврежденности с включенными компонентами тензора поврежденности в определяющие уравнения линейно-упругого материала была применена для оценки зон активного накопления повреждений у вершин трещины. На рис. 4–8 приведены результаты вычислений. На рис. 4–7 показаны распределения напряжений в пластине без учета процесса накопления повреждений (слева) и с учетом поврежденности материала (справа). Компоненты тензора поврежденности показаны на рис. 8. Из рис. 4–7 видно, что накопление повреждений приводит к снижению значений всех компонент тензора напряжений. Таким образом, влияние поврежденности в материале приводит к снижению особенности поля напряжений вблизи вершины трещины. На рис. 8, а и б при- ведены распределения компонент тензора поврежденно-сти D и D в пластине, связанные с максимальным и минимальным главными напряжениями.

о_п + G 22 ±j⁽c_u  O 22 ) + 4 G , 2

о, , о =----------------------------

12            ₂

В данном расчете компонента D связана со средним главным напряжением о = v ( o_n + о₂₂ ) .

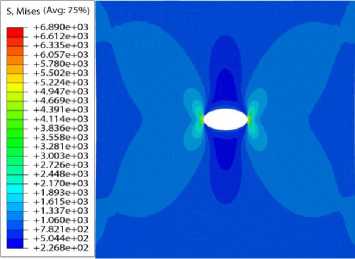
Рис. 4. Распределение интенсивности напряжений в пластине без учета накоплений повреждений ( а ) и с учетом накопления повреждений ( б )

Fig. 4. Distribution of stress intensities in the plate with no consideration of damage accumulation ( a ), and with the consideration of damage accumulation ( b )

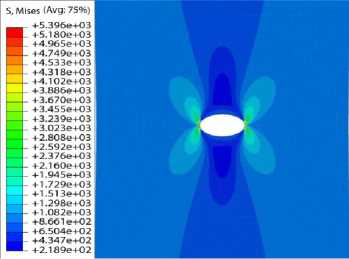
б

S, S11 (Avg: 75%)

.654е+03 449е+03 244е+03 ,039е+03 .835е+03 б30е+03 ,425е+03 .220е+03 .015е+03

606е+03 ,401е+03 .19бе+03 913е+02 .86564-02 .81764-02 .76964-02 .7216+02 .27264-01 .37564-02 .4236+02 .4726+02 .5206+02 .0576+03

б

Рис. 5. Распределение компоненты напряжений а_п в пластине без учета накоплений повреждений ( а ) и с учетом накопления повреждений ( б )

Fig. 5. Distribution of stress component a_n in the plate with no consideration of damage accumulation ( a ), with the consideration of damage accumulation ( b )

б

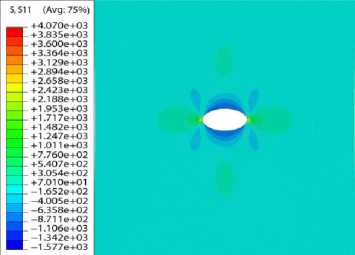
Рис. 6. Распределение компоненты напряжений а₁₂ в пластине без учета накоплений повреждений ( а ) и с учетом накопления повреждений ( б )

Fig. 6. Distribution of stress component a₁₂ in the plate with no the consideration of damage accumulation ( a ), with the consideration of damage accumulation ( b )

а

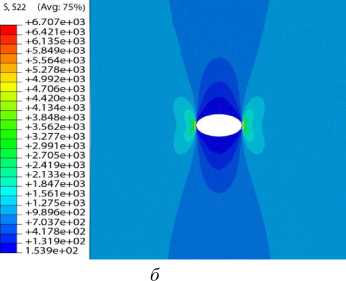
Рис. 7. Распределение компоненты напряжений σ в пластине без учета накоплений повреждений ( а ) и с учетом накопления повреждений ( б )

Fig. 7. Distribution of stress component σ in the plate: in the plate with no the consideration of damage accumulation ( a ), with the consideration of damage accumulation ( b )

б

Рис. 8. Распределение компонент тензора поврежденности: a – распределение компоненты D ; б – распределение компоненты D ; в – распределение компоненты D

Fig. 8. Distribution of damage tensor components: a – is the distribution of damage component D ; b – is damage component D distribution; c – is damage component D distribution

• 2.3.    Распределение поврежденности у вершин наклонной трещины в растягиваемой пластине

Для моделирования смешанного нагружения в полном диапазоне смешанных форм деформирования в работе была выполнена серия конечно-элементных расчетов для наклонной трещины в растягиваемой по оси ординат пластине.

На рис. 9–11 показаны распределения компонент тензора поврежденности для наклонной под углом α= 45 трещины. На рис. 12–16 приведены распределения интенсивности напряжений и компонент тензора напряжений в пластине с наклонной трещиной без учета накоплений повреждений (слева) и с учетом накопления повреждений (справа). Сравнение результатов расчетов для неповрежденного и поврежденного материалов показало, что учет процессов накопления повреждений приводит к снижению значений компонент тензора напряжений и интенсивности касательных напряжений в образцах с концентраторами напряжений, что хорошо согласуется с аналитическими и численными решениями краевых задач о трещинах

[25, 26]: учет процесса накопления повреждений приводит к ослаблению или полному устранению особенности поля напряжений у вершины трещины в изотропных линейно-упругих телах.

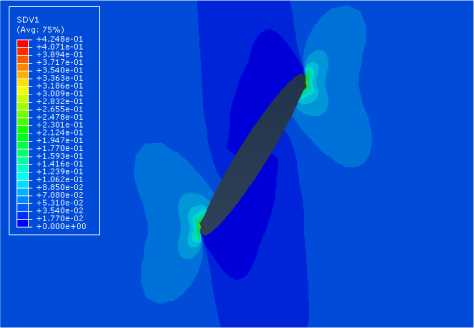
Рис. 9. Распределение компоненты тензора поврежденности D в растягиваемой пластине Fig. 9. Damage tensor component D distribution in the cracked plate under tension

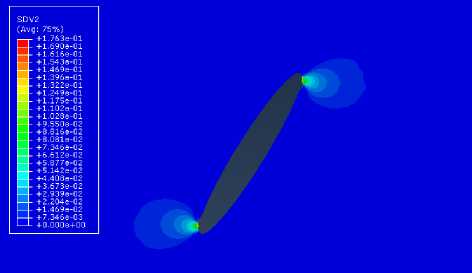
Рис. 10. Распределение компоненты тензора поврежденности D в растягиваемой пластине Fig. 10. Damage tensor component D distribution in the cracked plate under tension

Рис. 11. Распределение компоненты тензора поврежденности D в растягиваемой пластине с наклонной трещиной

Fig. 11. Damage tensor component D distribution in the cracked plate under tension

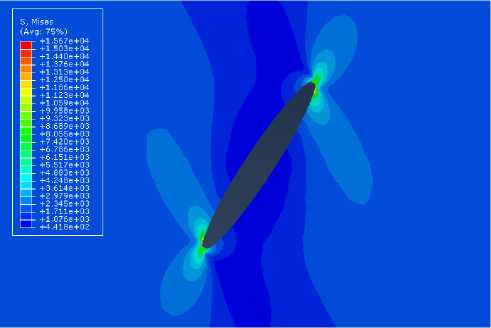
Рис. 12. Распределение интенсивности напряжений в пластине с наклонной трещиной без учета накоплений повреждений ( а ) и с учетом накопления повреждений ( б ) Fig. 12. Distribution of stress intensities in the plate with an inclined crack: with no consideration of damage accumulation ( a ), and with the consideration of damage accumulation ( b )

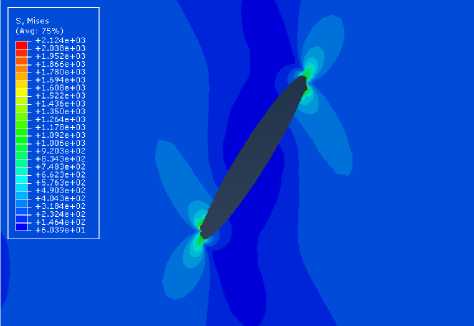
б

i±±ttttt±tffl

а

б

Рис. 13. Распределение компоненты напряжений σ в пластине без учета накоплений повреждений ( а ) и с учетом накопления повреждений ( б )

Fig. 13. Stress component σ distribution in the plate: with no consideration of damage accumulation ( a ), and with the consideration of damage accumulation ( b )

а

б

Рис. 14. Распределение компоненты напряжений σ в пластине без учета накоплений повреждений ( а ) и с учетом накопления повреждений ( б )

Fig. 14. Stress component σ distribution: with no consideration of damage accumulation ( a ), and with the consideration of damage accumulation ( b )

а

б

а

Рис. 16. Распределение компоненты напряжений σ в пластине без учета накоплений повреждений ( а ) и с учетом накопления повреждений ( б )

Fig. 16. Stress component σ distribution: with no consideration of damage accumulation ( a ), and with the consideration of damage accumulation ( b )

Рис. 15. Распределение компоненты напряжений σ в пластине без учета накоплений повреждений ( а ) и с учетом накопления повреждений ( б )

Fig. 15. Stress component σ distribution: with no consideration of damage accumulation ( a ), and with the consideration of damage accumulation ( b )

б

• 2.4.    Распределение поврежденности у вершины надреза в полудиске

Одним из часто рассматриваемых образцов является полудиск с вертикальным и наклонным надрезом [52– 55]. Геометрия образца и система приложенных нагрузок показана на рис. 17.

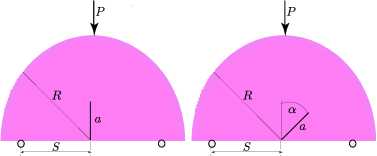
Рис. 17. Схематичное изображение образцов с надрезом для исследования нормального отрыва ( а ) и смешанного нагружения ( б )

Fig. 17. General configuration of the semicircular bend (SCB) specimen with a cut for Mode I loading ( a ) and Mixed Mode loadings ( b )

На рис. 17 приняты следующие обозначения: P – приложенная нагрузка; a – длина выреза; R – радиус диска; а - угол наклона надреза. Меняя угол наклона надреза а к вертикали, можно менять вид смешанного нагружения от нормального отрыва до нагружений, близких к поперечному сдвигу. В работе выполнена большая серия вычислительных экспериментов на трехточечный изгиб диска с надрезом в полном диапазоне значений угла а. Результаты вычислений показаны на рис. 18–26. На примере данной конфигурации была исследована зависимость распределения напряжений и поврежденности от вида разбиения, что является характерной особенностью задач механики поврежденности [22]. Проведенные расчеты не показали такой зависимости, и полученные распределения компонент тензора поврежденности (рис. 18–21), и компонент тензора напряжений (рис. 22–26) не зависят от способа разбиения, от вида конечных элементов. В ходе вычислений были

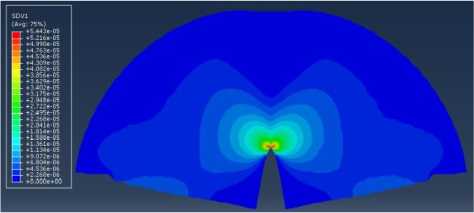
a

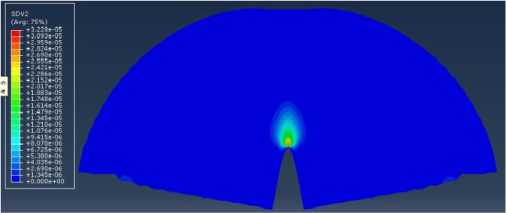
б

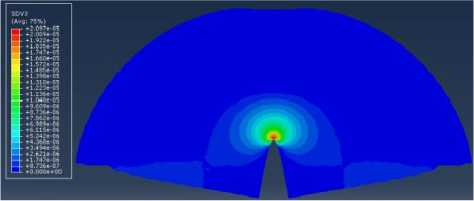
в

Рис. 18. Распределение компонент тензора поврежденности в диске с надрезом (нормальный отрыв): а – распределение компоненты D ; б – распределение компоненты D ; в – распределение компоненты D

Fig. 18. Distribution of the anisotropic damage tensor components: a – is damage tensor component D ;

b – is damage tensor component D ; c – is damage tensor component D .

проведены расчеты на различных сетках: менялось количество конечных элементов сетки и сравнивались значения искомых величин (компонент тензоров напряжений и повреждений) в совпадающих точках. Сравнение результатов показало, что измельчение сетки не ведет к изменению вычисленных значений для полей напряжений и поврежденности.

Распределение компонент тензора поврежденности в образце с наклонным под углом надрезом а = 30° показано на рис. 19–21.

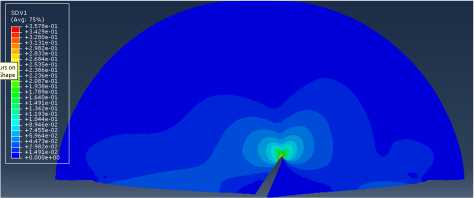
Рис. 19. Распределение компоненты тензора поврежденности D

Fig. 19. Distribution of the anisotropic damage tensor component D

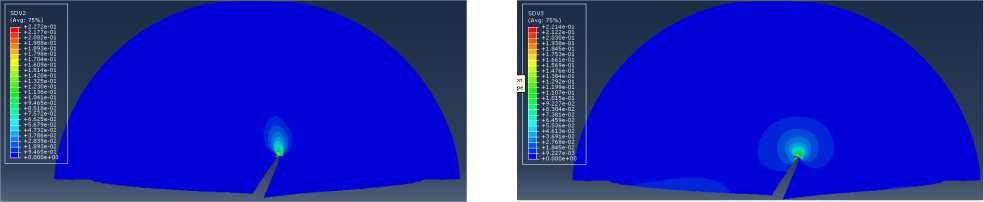
Рис. 21. Распределение компоненты D

Fig. 21. Distribution of the anisotropic damage tensor component D

Рис. 20. Распределение компоненты D

Fig. 20. Distribution of the anisotropic damage tensor component D

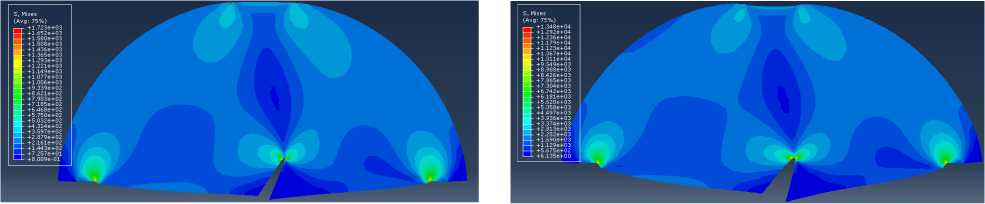
а                                                     б

Рис. 22. Распределение интенсивности напряжений в полудиске с наклонным надрезом без учета процесса накопления повреждений ( а ) и с учетом процесса накопления повреждений ( б ) Fig. 22. Distribution of the Mises equivalent stress in the SCB specimen with an inclined cut with no consideration of damage accumulation process ( a ) and with the consideration of damage accumulation processes ( b )

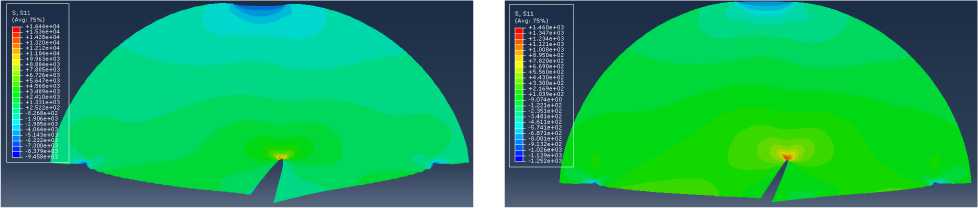
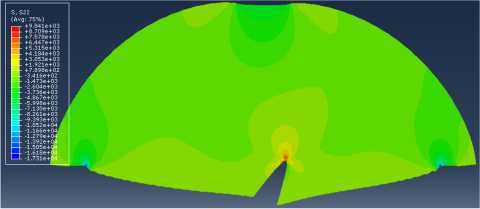
Рис. 24. Распределение компоненты тензора напряжений

Fig. 24. Distribution of the stress tensor component g₂₂

Рис. 23. Распределение компоненты тензора напряжений ст_п в полудиске с наклонным под углом а = 45° надрезом

Fig. 23. Distribution of the stress tensor component q_h in the SCB specimen with an inclined cut with an angle of а = 45°

q₂₂ в полудиске с наклонным под углом а = 45° надрезом in the SCB specimen with an inclined angle of а = 45°

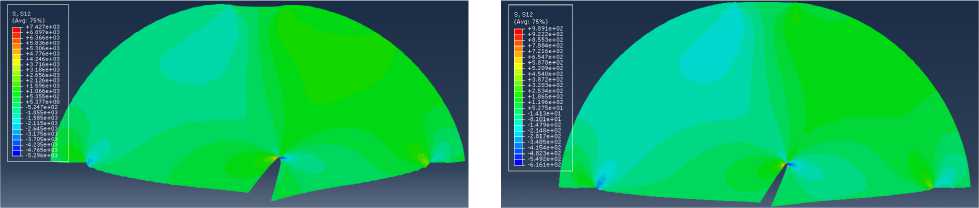
Рис. 25. Распределение компоненты тензора напряжений qI2 в полудиске с наклонным под углом а = 45° надрезом

Fig. 25. Distribution of the stress tensor component q_I2

in the SCB specimen with an inclined angle of а = 45°

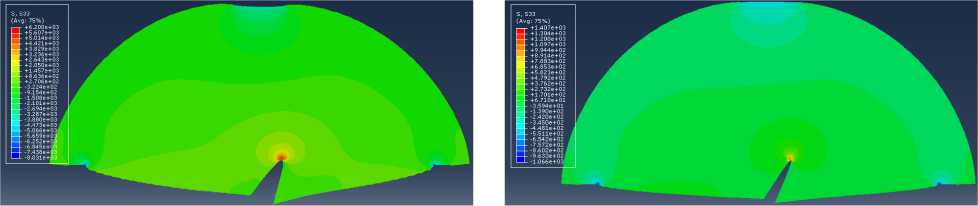
Рис. 26. Распределение компоненты тензора напряжений с₃₃ в полудиске с наклонным под углом а = 45° надрезом

Fig. 26. Distribution of the stress tensor component g₃₃ in the SCB specimen with an inclined angle of а = 45°

Выводы и обсуждение результатов

В настоящей работе описана и реализована процедура расчета поля анизотропной поврежденности в образцах с трещинами посредством моделирования определяющих уравнений связанной постановки задачи в связке упругость–поврежденность с помощью модели анизотропной поврежденности. В конечно-элементном комплексе SIMULIA Abaqus с помощью пользовательской процедуры UMAT реализована математическая модель материала с включенными компонентами тензора поврежденности второго ранга. Учтен анизотропный характер накопления повреждений в образцах с различной геометрией и различными системами нагрузок: рассмотрены пластина с центральной горизонтальной и наклонной трещиной и полудиск с вертикальным и наклонными надрезами. Получены и проанализированы зоны активного накопления повреждений вблизи кончика трещины и надреза для целой серии экспериментальных образцов с дефектами в условиях смешанного нагружения в полном диапазоне смешанных форм деформирования от чистого нормального отрыва до нагружений, близких к поперечному сдвигу. На основании проведенных расчетов для различных образцов с трещинами и надрезами показано, что накопление поврежденности приводит к снижению уровня напряжений вблизи вершины трещины, что хорошо согласуется с имеющимися аналитическими и численными решениями.