Компьютерное моделирование сечения неупругого рассеяния электронов в трехслойных структурах типа "пленка-интерфейс-подложка"

Количественная информация о сечении неупругого рассеяния электронов в твердом теле играет важную роль в поверхностно-чувствительных методах исследования поверхности, таких как электронная оже-спектроскопия, рентгеновская фотоэлектронная спектроскопия, спектроскопия характеристических потерь энергии электронов и др. Этот параметр определяет среднюю длину неупругого пробега электронов, фон электронных спектров, вклад поверхностных возбуждений в электронный спектр. Дважды дифференциальное сечение неупругого рассеяния электронов (s), движущихся в бесконечном однородном твердом теле, связано с его комплексной диэлектрической проницаемостью е ( к, ю ) соотношением [1] d 2 а         1 _т f 1

——7— =---Im —7 7- d (ho) dk na 0 kE I е (к, ю)

где E – энергия электрона; hω и k – изменение (всегда потеря) энергии и волновое число электрона в результате неупругого рассеяния соответственно; a ₀ – радиус Бора.

Интегрирование выражения (1) по всем возможным значениям изменения волнового числа в процессе неупругого взаимодействия электрона со средой дает выра- жение для дифференциального сечения по потерям энергии hω

— = K ( E,h o ) =       f dk Im ^f-    '    ^ ,   (2)

dh®     v 7 na0EkL к | e(к,ю) J где к± = ±. 2m- (VE ± Ee - hto) h2

. Это интегрирование экви-

валентно интегрированию по всем возможным значениям углов неупругого рассеяния электронов. Единицей измерения K ( E , hm ) является произведение обратной длины на обратную энергию. Величина K ( E, h® ) рассматривается как вероятность того, что на единице длины пути на единицу энергии электрон потеряет энергию h ® . Функция K ( E, hm ) имеет структуру, связанную с возбуждением плазмонов на частоте плазменных колебаний ю p .

В связи с тем, что методики, позволяющие рассчитать сечение неупругого рассеяния из экспериментальных спектров, представляют его в интегральном (по длине пути) виде, зачастую при теоретическом моделировании рассчитывают именно эту величину Для K (E, hm), представленного формулой (2), интегральной величиной бу- дет произведение K (E, Йю) на длину неупругого свободного пробега электронов в данном материале [2]. В более сложных моделях для расчета интегрального сечения неупругого рассеяния может потребоваться интегрирование дифференциальной величины.

Длину неупругого свободного пробега электрона в веществе, а точнее, ее обратную величину, можно определить путем интегрирования уравнения (2) по всем воз-

кие электроны могут с разной вероятностью достигать разных глубин внутри твердого тела; вероятность того, что электрон испытал только одно неупругое взаимодействие, пропорциональна ( x )exp( - x / X) [4]. Интегральное

сечение однократного неупругого рассеяния электронов может быть найдено как средневзвешенная величина от K _eff с весовой функцией ( x / X)exp( - x / X ). Проинтегрировав знаменатель аналитически, в окончательном виде

можным потерям энергии:

1(E)

от

= j K (E, Йю) d (Йю).

интегральное сечение однократного неупругого рассеяния можно представить следующей формулой:

Цель данной работы заключалась в расчете сечения

неупругого рассеяния в трехслойных структурах на ос-

нове существующей модели сечения неупругого рассе-

1 от

X K ( E , Йю) = — J x exp( - x / X ) K_ff ( E , Й ю , x , £ ) dx . (5)

X 0

Комплексная диэлектрическая функция среды, согласно модели Друде–Линдхарда, может быть представлена в

яния в однородном материале.

Методика расчетов. В основе алгоритма программы

лежит модель расчета сечения неупругого рассеяния, предложенная в работе [3]. Модель позволяет рассчитать

виде суперпозиции Лоренцевых осцилляторов, каждый из которых имеет свою собственную частоту m i , силу A и коэффициент затухания у . [4]:

сечение неупругого рассеяния для электрона, нормально падающего из бесконечности на поверхность материала, затем упруго отраженного на некоторой глубине a в противоположную сторону и при этом испытавшего за время своего движения внутри твердого тела одно неупругое столкновение. Данная модель основана на теории диэлектрического отклика, которая предполагает, что все свойства твердого тела, отвечающие за его взаимодействие с внешними электронами, описываются диэлектрической функцией данного твердого тела. Авторами модели было предложено выражение для нахождения эффективного сечения неупругого рассеяния электронов K _eff, которое имеет смысл дифференциального сечения неупругого рассеяния электрона:

£( k, ю) = 1 + У------:—Ai---;------ i (mi + k2 / 2)2 - ю2 + imyi

.

Число осцилляторов, частота, сила и коэффициент затухания каждого из них обычно определяют из опти-

ческих данных или экспериментов по неупругому рассеянию электронов. В ряде работ [5–7] параметры Друде– Линдхарда используются для вычислений действительной и мнимой частей диэлектрической функции, в других [8– 10] по этим параметрам вычисляют непосредственно мнимую часть отрицательной обратной величины диэлектрической функции (функцию потерь).

Ранее нами была разработана компьютерная програм-

K ef ⁽ E 0 , ^Й ® , x 0 ) =

- 2 exp(2) h ²π v ²

Re x

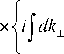
1 ^ k ₁ | - 2exp(2) 1

£ J k 1 + y ² Й ² п v m 2 a

x Re - i j dk ₁ -———— x [ (2 yk ₁ exp( - k ₁ a ))(4cos( ya ) -

1 - £(

• -    exp( - k ₁ a ))-- + ( k 1 2 - y ²) sm(2 ya ) I — 1

£(1 + £)

• -    2 yk J— 1 II 1 + 2cos²( ya )----

• (s Д1

где E и v - энергия и скорость электрона соответственно; £ - диэлектрическая проницаемость материала, в котором происходит рассеяние; x = 2 a - путь, пройденный электроном в твердом теле. K _eff ( E , Йю, a , е ) является функцией тех же параметров, что и сечение, представленное уравнением (2), за исключением глубины упругого рассеяния электронов a .

Методика нахождения K _eff позволяет рассчитать дифференциальное сечение неупругого рассеяния электрона, достигшего любой глубины в твердом теле и испытавшего произвольное количество неупругих взаимодействий. Для вычисления сечения однократного неупругого рассеяния необходимо учесть только те электроны, которые испытали одно неупругое взаимодействие. Та-

ма для численного расчета сечения неупругого рассеяния электронов для полубесконечного однородного образца в соответствии с приведенной выше моделью [11]. В данной работе было произведено расширение модели на случай, когда среда, с которой взаимодействует электрон, состоит из трех слоев: пленки, которая может формироваться как в виде островков, так и сплошного слоя, интерфейса и подложки (рис. 1).

Предполагается, что вклад в сечение неупругого рассеяния электронов, потерявших энергию в результате неупругого взаимодействия на определенном расстоянии x от поверхности слоистой структуры, определяется диэлектрическими свойствами среды в данной точке с соответствующей весовой функцией. С учетом этого предположения и выражения (5) интегральное сечение неупругого рассеяния в трехслойной структуре с толщиной пленки d и толщиной промежуточного слоя dm может быть представлено суммой вкладов от взаимодействия

электронов со слоями:

X KSC3 i_ay ( E , w, dm , d ) =

1 ^{2 d}

= t— j x exp( - x / X _f ) K _eff ( E , w , x ,£ _f ) dx +

^X f 0

2( d + dm )

+ j

2 d

x exp( - x / X _f ) M ( x ) Keff ( E , w , x , £ _f )

X

+

x exp( - x / X _s )(1 - M ( x )) K eff ( E , w , x , £ _s )

X _s

1 ОТ

+— j     x exp( - x / X _s ) K _eff ( E , w , x , £ _s ) dx .

^X » 2( d + dm )

dx + , (7)

Индексы f и S относятся соответственно к пленке и подложке; M ( x ) – функция, описывающая относительное содержание материала пленки на глубине x в промежуточном слое. При dm = 0 уравнение (7) переходит в формулу для расчета сечения неупругого рассеяния в двухслойной структуре. При d = dm = 0 уравнение (7) отражает исходную простейшую модель, предложенную Юбе-ро и Тоугаардом [3].

Формально такая структура является более сложной разновидностью двухслойной структуры, в которой в результате диффузии между материалами пленки и подложки образовался промежуточный слой, в котором каким-то образом распределены материалы пленки и подложки. Второе слагаемое в уравнении (7) описывает вклад в сечение от взаимодействия электронов с промежуточным слоем. В плоскости, перпендикулярной вектору скорости движения электрона , структура предполагается однородной. В программе реализованы 3 варианта распределения компонент в промежуточном слое.

Первый вариант – самый простой, в нем функция M ( x ) не зависит от глубины и равна объемной доле материала верхнего слоя в промежуточном – M ( x ) =V _upper. Во втором случае предполагается, что концентрация материала пленки в промежуточном слое линейно уменьшается с глубиной и M ( x ) = 1 – ( x – 2 d )/(2 dm ). Таким образом, содержание материала верхнего слоя равно единице на границе между промежуточным и верхним слоем и нулю на границе между подложкой и интерфейсом. В третьем варианте реализовано экспоненциальное изменение содержания материалов с глубиной – M ( x ) = exp(–4 ∙ ( x – 2 d )/(2 dm )).

Как известно, рост пленки на подложке может происходить с образованием островков, высота которых бывает значительно больше толщины атомного слоя. Относительная площадь поверхности, занимаемая островками, характеризуется степенью покрытия и. Если ширина пучка первичных электронов намного больше размеров островка, то можно допустить что θ ∙100 % первичных электронов падают на островки и взаимодействуют с трехслойной структурой «пленка–интерфейс–подложка», а ос- тальные [1–θ ]∙100 % падают в области, где нет островков, и взаимодействуют с двухслойной структурой «интерфейс–подложка». Предполагая достаточно большие размеры отдельного островка (но по-прежнему много меньшие размеров электронного пучка), можно допустить, что число электронов, падающих близко к стенкам островков, и, значит, испытывающее дополнительные потери от взаимодействия с поверхностным зарядом, образовавшимся на стенках островков, достаточно мало. В этом случае интегральное сечение неупругого взаимодействия электронов с островковой структурой можно представить в следующем виде:

λ Ksc_isl ( E , w , dm , d ) = θ ⋅ λ Ksc _{3 lay} ( E , w , dm , d ) + + (1 -θ ) ⋅λ Ksc _{3 lay} ( E , w , dm , d = 0). ⁽⁸⁾

При θ = 1, т. е. когда островки превращаются в сплошной слой, данное выражение переходит в выражение (7).

Структура программы. Структурная схема программы MLCS (Multi-Layered Cross-Sections), позволяющей проводить моделирование сечений неупругого рассеяния в слоистых средах, приведена на рис. 2. Входными параметрами являются энергия первичных электронов ( E ), толщина пленки ( d ), толщина промежуточного слоя ( dm ), степень покрытия островками (и) (в случае модели с островками), длины свободного неупругого пробега электронов ( λ ) в пленке и подложке, параметры диэлектрических функций ( A_i , ω _i , γ _i ) материалов пленки и подложки, максимальное значение hω рассчитываемых значений потерь энергии. Все параметры, относящиеся к пленке, обозначены на рисунке индексом f , а к подложке – индексом s .

Параметры диэлектрической функции материала, используемые в программе, хранятся в базе данных sqlite. Они могут быть добавлены или отредактированы с помощью встроенного в программу редактора параметров.

На первом этапе рассчитываются с использованием заданных параметров A_i , ω _i , γ _i диэлектрические функции материалов пленки и подложки. Затем с использованием рассчитанных диэлектрических функций, энергии первич-

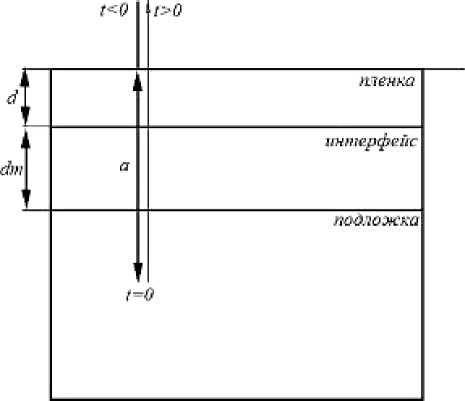
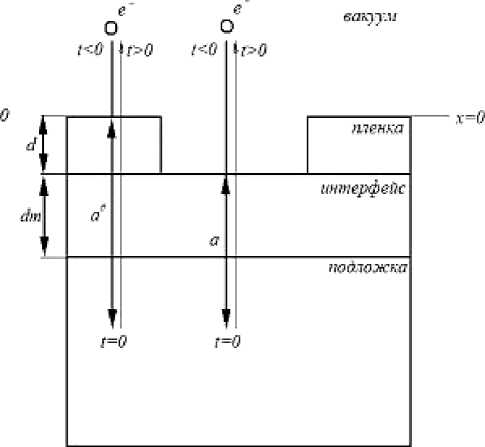
Рис. 1. Схема взаимодействия электрона с образцом для случая послойного роста пленки (слева) и роста пленки с образованием островков (справа)

ных электронов и длин неупругого свободного пробега электронов в заданном диапазоне вычисляется эффективное сечение неупругого рассеяния электронов в верхнем и нижнем слое как функция потери энергии электронов. Из эффективных дифференциальных сечений неупругого рассеяния в пленке и подложке, с учетом толщины пленки и толщины промежуточного слоя, рассчитываются вклады в интегральное сечение неупругого рассеяния от пленки, подложки и промежуточного слоя (характер распределения материалов в промежуточном слое выбирается пользователем). Результаты расчетов могут быть выведены на экран и сохранены в текстовом файле для дальнейшей обработки.

Результаты расчетов и обсуждение. С использованием программы MLCS было проведено исследование потерь энергии электронов в слоистых трехслойных структурах «Fe–интерфейс–Si» (пленка железа, промежуточный слой Fe/Si, кремниевая подложка) для энергии первичных электронов 200 эВ. Длина неупругого свободного пробега электронов в железе при данной энергии составляет 5,79 Е, в кремнии – 7,62 Е. Даная структура была выбрана для исследования в связи с использованием этих материалов в электронике и перспективами использования в спинтронике. Зависимости сечения неупругого рассеяния от энергии потерь электронов для железа и кремния существенно отличаются формой линии и интенсивностью. Так, максимум зависимости сечения неупругого рассеяния электронов в Si примерно в 2,5 раза превышает значение максимума сечения в Fe. В то же время, при малых потерях интегральное сечение неупругого рассеяния интенсивней для железа за счет более выраженного поверхностного плазмона. Это позволяет существенно облегчить определение того или иного эле- мента в сечении неупругого рассеяния трехслойной структуры, составленной из железа и кремния.

Для исследования влияния распределения элементов в промежуточном слое на потери энергии электронов, расчетные параметры были выбраны таким образом, чтобы структура была эквивалентна сплошной пленке железа толщиной 15 Е на поверхности кремниевой подложки без промежуточного слоя. Интегральные сечения неупругого рассеяния электронов для различных распределений элементов в промежуточном слое представлены на рис. 3. Верхняя и нижняя диаграммы – результаты моделирования для кремния и железа соответственно. Три промежуточных диаграммы (снизу вверх) соответствуют структуре с пленкой толщиной 15 Е без промежуточного слоя; структуре без слоя пленки, но с промежуточным слоем толщиной 30 Е, в котором железо и кремний присутствуют в постоянных, независимых от расстояния от поверхности, равных долях; структуре без пленки, но с промежуточным слоем толщиной порядка 61 Е, в котором элементы распределены экспоненциальным образом.

Несмотря на одно и то же содержание железа, рассматриваемые структуры существенно различичаются. Для структуры без промежуточного слоя характерно наибольшее влияние пленки на потери энергии. Это связано с тем, что при заданной энергии первичных электронов длина неупругого свободного пробега электронов в железе меньше толщины пленки Fe (5,79 и 15 Е) и, следовательно, большая часть электронов рассеивается именно в ней. Наименьший вклад железа в сечение неупругого рассеяния наблюдается для структур с постоянным распределением элементов. В случае экспоненциального распределения компонент в промежуточном слое влияние пленки больше чем при постоянном распределении,

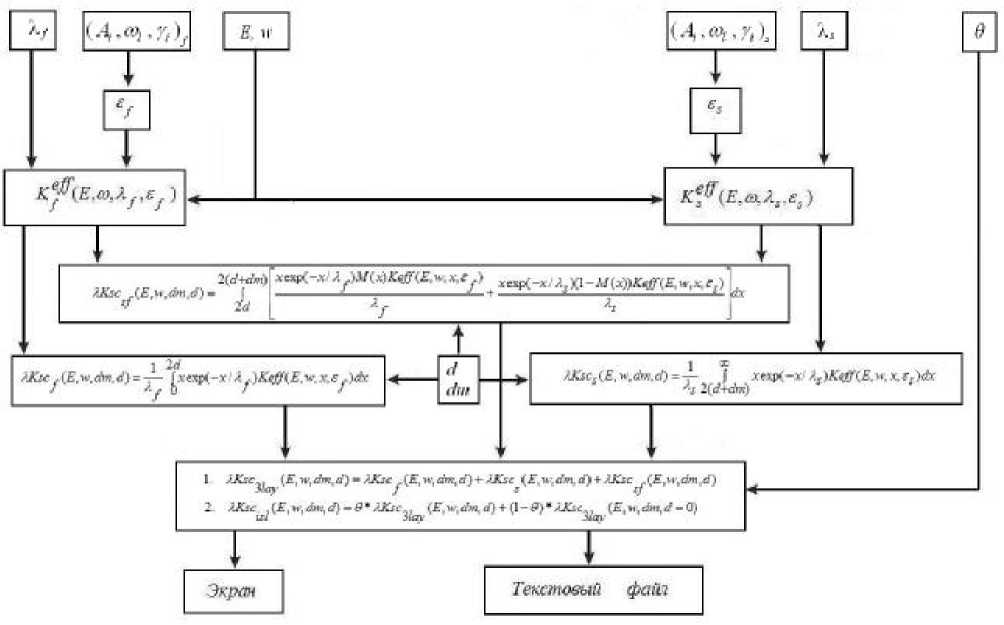
Рис. 2. Структурная схема компьютерной программы MLCS

но меньше, чем в случае структуры с резкой границей между слоями.

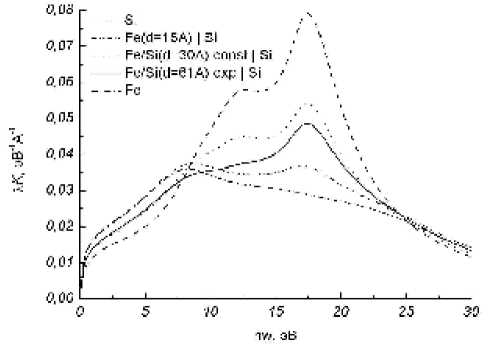
Рис. 3. Зависимости λ K от потери энергии электронов в трехслойной структуре «Fe–интерфейс–Si» при одинаковом содержании железа и различных распределениях элементов в промежуточном слое при первичной энергии электронов 200 эВ

Для изучения влияния островков был произведен расчет сечения неупругого рассеяния в трех структурах: структура без островков с толщиной пленки 15 Е и толщиной промежуточного слоя 5 Е; структура с островками высотой 30 Е, степенью покрытия 0,5 и промежуточным слоем толщиной 5 Е; структура с островками высотой 60 Е, степенью покрытия 0,25 и промежуточным слоем толщиной 5 Е. В интерфейсе элементы имели постоянное распределение с равными долями. Энергия первичных электронов составляла 500 эВ. Параметры структуры выбраны таким образом, чтобы содержание железа было постоянным и эквивалентным сплошному слою железа толщиной 17,5 Е на поверхности кремния. Результаты моделирования в этих структурах представлены на рис . 4.

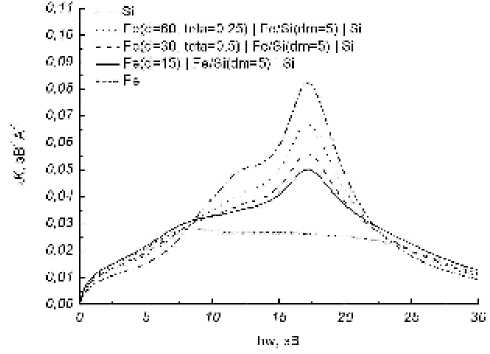
Рис. 4. Зависимости λ K от потери энергии электронов в трехслойных структурах, в которых верхний слой представлен в виде островков, при постоянном содержании железа и первичной энергии электронов 500 эВ

Верхний и нижний графики соответствуют сечению неупругого рассеяния в кремнии и железе. Видно, что для структуры с меньшей степенью заполнения поверхности островками наблюдается меньший вклад железа в сечение рассеяния, в то время как для структуры со сплошной пленкой этот вклад максимален. Это объясняется тем, что если островки редки, то большинство первичных электронов падают на области поверхности, где структура содержит меньше железа, в связи с этим его влияние на потери уменьшается.

В работе было произведено расширение модели расчета сечения неупругого рассеяния в однородном материале на случай трехслойной структуры, состоящей из пленки, которая может формироваться как в виде островков, так и сплошного слоя, интерфейса и подложки.

Разработана компьютерная программа, реализующая расчет для данной структуры, описана ее структура и алгоритм расчета.

Представлены результаты моделирования интегрального сечения неупругого рассеяния электронов в слоистой структуре «Fe–интерфейс–Si».

Результаты расчетов показали влияние распределения элементов в интерфейсе и степени заполнения островками поверхности подложки трехслойной структуры «Fe–интерфейс–Si» на интегральную зависимость произведения средней длины свободного неупругого пробега на сечение неупругого рассеяния электронов в данных структурах. Так как интегральные сечения неупругого рассеяния электронов могут быть непосредственно экспериментально определены из спектров потерь энергии отраженных электронов [12], моделирование этих зависимостей с помощью разработанной программы и сравнение с экспериментальными результатами может быть использовано для определения механизма роста структур, распределения элементов в пленке, оценки толщины пленки, толщины промежуточного слоя.