Компьютерное моделирование устойчивого социально-экономического развития России, Казахстана и Японии

Автор: Григорьева Кира Владимировна

Журнал: Сетевое научное издание «Устойчивое инновационное развитие: проектирование и управление» @journal-rypravleni

Статья в выпуске: 1 (26) т.11, 2015 года.

Бесплатный доступ

В статье описана концептуальная математическая модель, связанная с исследованием проблем устойчивого социально-экономического развития. Введены критерии устойчивого развития и принципы, на которых базируется модель устойчивого социально-экономического развития. Рассмотрено применение компьютерного моделирования на конкретных примерах на базе исходных данных по Российской Федерации, Казахстану и Японии за 2005-2011 год.

Мощность как инвариант, lt-система, величина [lt], пространственно-временные меры, закон сохранения мощности, "живые" системы, устойчивое социально-экономическое развитие

Короткий адрес: https://sciup.org/14123005

IDR: 14123005

Текст научной статьи Компьютерное моделирование устойчивого социально-экономического развития России, Казахстана и Японии

В настоящее время, на пороге нового века и нового тысячелетия, самая главная проблема, которая стоит перед Наукой мира в целом, - это обеспечение устойчивого исторического будущего человечества. Все государства, так или иначе, столкнулись с тяжелейшими проблемами, такими, как, например, проблемы энергообеспечения, экологии и здравоохранения. Становится очевидным, что большинство проблем порождено прямым или косвенным, осознаваемым или неосознаваемым нарушением законов Природы [9].

Академик М.М. Лаврентьев

На сегодняшний день опубликовано много работ, посвященных проблеме устойчивого развития. Как правило, в этих работах рассматриваются различные аспекты устойчивого развития при отсутствии их измеряемой взаимосвязи. Следствием этого является невозможность надежно проектировать и управлять устойчивым развитием разнородных систем.

том 11 № 1 (26), 2015, ст. 5

Крайне мало работ, в которых проблема проектирования и управления устойчивым развитием систем обсуждается в терминах универсальных системных мер, дающих возможность решения проблемы на основе математического моделирования.

Впервые удалось довести общепринятый мировым сообществом принцип устойчивого развития до максимальной конструктивности и рассматривать его в терминах целей, достижением которых можно управлять на основе общих законов сохранения и развития.

В настоящей статье рассмотрено компьютерное моделирование, связанное с исследованием проблем устойчивого социально-экономического развития на примере России, Казахстана и Японии.

1. Теоретические основы модели устойчивого развитиясоциально-экономических систем 1.1. Требования и структура модели

Необходимость научного обеспечения устойчивого развития предъявляет определенные требования к модели. К их числу, прежде всего, следует отнести:

1. Универсальность величин, используемых в модели [2, 4, 8].
2. Возможность работы с разнородной информацией с соблюдением принципов соразмерности [5]. Принцип соразмерности требует наличие правила, удовлетворяющего П-теореме [4].
3. Возможность работы с информацией в условиях неопределенности – в условиях, когда понятия не выражены в терминах универсальных величин.

Структура математической модели

Элементами модели являются язык, правила вывода, следствия, проверка (рис. 1).

Язык

Рис. 1. Структура математической модели

1.1.1. Метаязык модели

Метаязык модели опирается на систему универсальных величин (определяющих язык исходных терминов модели), представленной в виде таблицы пространственно-временных www.rypravlenie.ru

том 11 № 1 (26), 2015, ст. 5

величин с формулой размерности [LRTS] , где L – длина (см), Т – время (сек), R и S – целые числа (положительные и отрицательные) от минус до плюс бесконечности (рис. 2) [1, 2, 5, 6, 8, 10, 11, 12, 13].

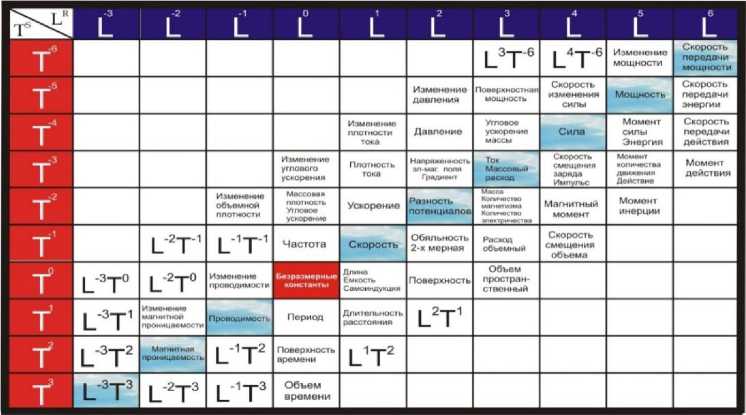
Рис. 2. Система пространственно-временных величин Р. Бартини-П. Кузнецов (LT-система)

Каждая величина в LT-системе [2,5]:

• это качественно-количественная мера-определенность: качество определяется именем, пространственно-временной LT-размерностью и единицей измерения, а количество – численным значением величины.
• это скаляр, вектор, тензор;
• это инвариант в определенном классе систем [2,8].

LT-система является классификатором систем реального мира [2, 4, 8]. Каждая величина является инвариантом (мерой-законом сохранения) определенного класса систем [2, 4]. Границы одного класса систем определяются размерностью LT-величины [4, 6, 8]. Переход в другой класс систем означает изменение LT-размерности величины. Мерой-законом сохранения в LT-системе является утверждение о том, что величина [LRTS ] является инвариантом в определенной системе координат, определяемой размерностью LT-величины [2, 8].

Стандартная запись закона сохранения [L R T S ] = const. [1, 2, 8] Закон сохранения энергии, например, записывается как [L 5 T - 4 ] = const. [2, 4, 5]. Закон сохранения мощности, являющийся базовым в теории устойчивого развития, записывается как [L 5 T - 5 ] = const [5, 8].

том 11 № 1 (26), 2015, ст. 5

LT-система является бесконечной. Это означает, что не существует ограничений на количество содержащихся в ней величин и мер-законов. В ходе развития научной мысли их список будет все время пополняться [4, 5, 8].

1.1.2. Аксиомы модели

Аксиома существования.

Объект существует, если он сохраняется и изменяется во времени-пространстве [1, 3, 4, 6, 7, 8].

Аксиома 1. Сохранение.

Аксиомой сохранения объекта является закон сохранения потока энергии или мощности (Лагранж, Д. Максвелл, В.И. Вернадский, Г. Крон, П. Г. Кузнецов), как общий закон Природы, лежащий в основе сохранения живых систем.

Полная мощность системы равна сумме полезной мощности и мощности потерь [4, 8]:

N = P + G, [L 5 T - 5 ] (1)

dE где N = —, [L5T ] - полная мощность или потоки энергии на входе в систему E; dt

P = —, [L5T-5] – полезная мощность на выходе или потоки превратимой энергии B; dt dA

G =---, [L 5 T ] - мощность потерь или потоки связной, непревратимой энергии A;

Р ф = —, [LUTU ] - эффективность использования полной мощности.

Аксиома 2. Изменение.

Аксиома изменения объекта описывается скалярным уравнением с разными граничными условиями [4, 5, 14]:

0 = P + G i , где G i =G-N, [L 5 T - 5 ],

где

G_Y > 0 для процессов Р. Клаузиуса (диссипативные процессы) [4, 12, 14],

G_Y < 0 для процессов Э. Бауэра (антидиссипативные процессы) [3, 4, 14],

G_y = 0 для процессов переходного типа [4, 14].

1.1.3. Формулизмы – параметры модели

Все социально-экономические системы, несмотря на их разнообразие, обладают общими свойствами и подчиняются общим законам. Любая система обладает мощностью, что и позволяет ей совершать работу во времени. Способность живых систем принимать и расходовать потоки энергии обеспечивает возможность описания (формализации) любой системы в энергетических показателях. Такая формализация позволяет моделировать процессы, протекающие в сложных системах, и находить новые решения ранее проблемных задач.

На основе метаязыка и введенных аксиом выделяются формулизмы–параметры, с помощью которых описывается процесс сохранения развития систем любой природы. В таблице показано полнозаданное описание.

Таблица 1. Формулизмы-параметры модели

№	Название	Условное обозначение	Единицы измерения	Формулы	LT-размерность
Базовые индикаторы
1	Полная мощность или суммарное потребление природных энергоресурсов за определенный период времени	N(t)	(Вт, кВт, МВт, ГВт)	nco=e E^Nu(o N j,(t),N _j2(t) . N_j3(t) - суммарное потребление j-го объекта управления в единицах мощности; Np — суммарное потребление продуктов питания; Nj₂ — суммарное потребление электроэнергии; Nj3 - суммарное потребление топлива	[l⁵t⁵i
2	Полезная мощность, совокупный произведенный или конечный продукт за определенный период времени	Р(0	(Вт, кВт, МВт, ГВт)	P(t) = N(t)r\|(t)-e(t) r\|(t) — обобщенный КПД технологий c(t) — качество планирования	[Ь⁵Т⁵]
3	Потери мощности за определенный период времени	G(t)	(Вт, кВт, МВт, ГВт)	G(t) = N(t)-P(t)	[L⁵T⁵]
4	Эффскти вность использования ресурсов или полной мощности на определенный период времени	<Р(О	безраз-мерные единицы	N(0	[\|."Т°]
5	Совокупный уровень жизни	U(t)	ватт на человека	U(t) = ^; M(t) M(t) — численность населения	[L’T⁵]
6	Качество окружающей природной среды	q(t)	безраз -мерные единицы	q(t>₌ G<.^1_; G(t) G(t) и G(t т) мощность потерь текущего и предыдущего периода	[L°T]
7	Качество жизни	QUO	ватт на человека	ОНО T_A(t)-U(t)-q(t); T_A(t) — нормированная продолжительность жизни; T_A(t) = ^Т‘"¹¹⁾ . 100 лет где T^t) — средняя продолжительность жизни	[lT⁵]
8	Мощность валюты (мощность единицы валюты)	W(t>	ватт на денежную единицу	w₍o- VP(t)	[L’T⁵]
9	Реальный конечный продукт в денежных единицах	P,(t)	денежные единицы, обеспеченные полезной мощностью	Pp(t) = P(t) - Vo v₀ — постоянная конвертации, полученная из условия единичной мощности валюты на to	димензиальн д остато чныс денежные единицы
10	Номинальный конечный продукт в текущих ценах	vp(t)	денежные единицы	VP(t) = ^VP/t) VP,(t) — стоимость реализованных товаров и услуг j-ro объекта	нс имеет LT-размсрности
11	Спекулятивн ы й капитал	SK(t)	денежные единицы, нс обеспеченные полезной мощностью	SK(t) = VP(t)-P,(t)	не имеет LT-размсрности

1.1.4. Правила вывода
Рост – увеличение полезной	[ dP > 0	Развитие – увеличение	I dP > 0
	dt		dt
мощности системы в основном за 1	dN > 0	полезной мощности системы в	dN ■ 0
счет роста полной мощности, а не	dt		dt
счет роста полной мощности, а не	d^ _{= o}	основном за счет повышения	d^ _> o
за счет увеличения эффективности	_ dt	эффективности использования	. dt
ее использования.		полной мощности, а не за счет
		увеличения полной мощности.

При исследовании социально-экономических систем разного уровня иерархии (мир, группы стран, страна, область, регион, отрасль, предприятие) к базовым параметрам устойчивого развитии (N, P, G, (р ) для анализа добавляются дополнительные параметры, такие как уровень жизни ^ = ^ и качество окружающей среды q = |° •

Устойчивое развитие – это сохранение развития в длительной перспективе Т в условиях негативных внутренних и внешних воздействий за счет неубывающего темпа роста эффективности использования полной мощности, повышения уровня жизни и качества окружающей среды при неувеличении темпов роста полной мощности: Негативные внутренние и внешние воздействия – это угрозы и воздействия, уменьшающие полную и полезную мощность.

Рис. 3. Закон сохранения мощности

' P ( t ) = p + pt + P₂t ² + pt ³ + • • • > 0 n ( t ) = n_o + n^ + N₂t ²+ Nt ³ + • • • < 0

< M ( t ) = G_o + Gt t + G ₂ t ² + G₃t ³ + • • • > 0

U (t) = u_o + U_xt + U₂t ² + U₃t ³₊...> 0 q (t ) = q ₀ + q_tt + q₂ t ² + q₃t ³ + • • • > 0

При исследовании социально-экономических систем разного уровня иерархии (мир, группы стран, страна, область, регион, отрасль, предприятие) были сформулированы возможные сценарии развития объекта управления. Они основаны на комбинации динамики 5 параметров: численность населения (M), совокупное производство (полезная мощность P), суммарное потребление (полная мощность N), совокупный уровень жизни (U) и качество окружающей среды (q).

Критерии опережающего устойчивого развития социально-экономической системы:

Вариант 1: 1) ^>0,2) ^ > 0, 3) ^ < 0, 4) ^^ > 0, 5) ^^ > 0 (4)

Вариант 2: 1) ^>0,2) ^ > 0, 3) ^ < 0, 4) ^^ > 0, 5) ^^ < 0 (5)

том 11 № 1 (26), 2015, ст. 5

В данной статье показаны только скорости изменения показателей, но не их ускорение, рывок или более высокие производные.

1.1.5 Следствия модели

На основе пяти параметров (^, ^, ^-, ^, ^) может быть сформировано дерево целей, которое является классификатором логически возможных типов целей:

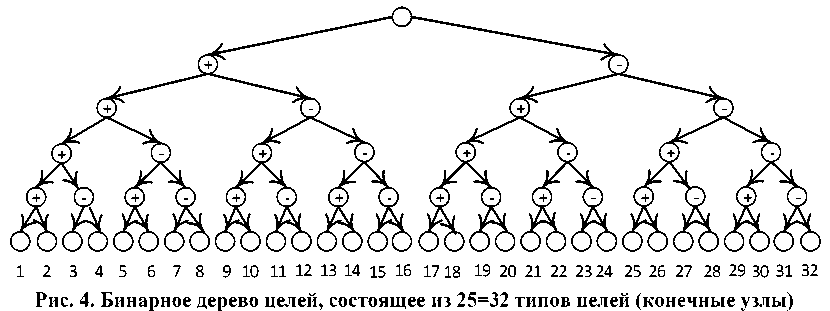
Эти 32 типа цели могут быть сгруппированы следующим образом:

1) Энергосырьевой сценарий (2, 4, 10, 12, 14, 16, 18, 20, 26, 28, 30, 32).
2) Индустриально-инновационное развитие (1, 3, 9, 11, 13, 15, 17, 19, 25, 27, 29, 31).
3) Устойчивое инновационное развитие (6, 7, 8, 21, 22, 23, 24).
4) Устойчивое развитие / Опережающее устойчивое развитие (5).

Пример 1. Справочник «Идентификация текущего состояния»

Тип состояния	Динамика параметров	Сценарий	Характерные черты	Описание и негативные следствия
	Энергосырьевой сценарий
2	• Численность населения не убывает (ДМ > 0) • Совокупное производство товаров и услуг (полезная мощность) не убывает (ДР > 0) • Суммарное потребление природных энергоресурсов не убывает (ДМ > 0) • Совокупный уровень жизни не убывает (AU > 0) * Качество окружающей природной среды убывает (Aq < 0)	Энергосырьевой или экстенсивный	Экстенсивный рост за счет опережающего роста энергопотребления (AN>0). следствием которого могут быть экологические (Aq<0). демографические (ДМ<0) и социально-экономические	Опережающий рост энергопотребления и, как следствие, угроза энергоэкологического кризиса (Aq<0)
4	• Численность населения не убывает (ДМ > 0) • Совокупное производство товаров и услуг (полезная мощность) не убывает (ДР > 0) • Суммарное потребление природных энергоресурсов не убывает (ДМ > 0) • Совокупный уровень жизни убывает (ДП < 0) • Качество окружающей природной среды убывает (Aq < 0)	Энергосырьевой или экстенсивный	Экстенсивный рост за счет опережающего роста энергопотребления (АКУ)), следствием которого могут быть экологические (Aq<0), демографические (АМ<0) и социально-экономические	Опережающий рост энергопотребления, ум еныпение с ов окупного уровня жизни (AU<0) и ухудшение качества
10	• Численность населения не убывает (ДМ > 0) • Совокупное производство товаров и услуг (полезная мощность) убывает (ДР < 0) • Суммарное потребление природных энергоресурсов не убывает (AN > 0) • Совокупный уровень жизни не убывает (AU > 0) • Качество окружающей природной среды убывает (Aq < 0)	Энергосырьевой или экстенсивный	Экстенсивный рост за счет опережающего роста энергопотребления (АХУО), следствием которого могут быть экологические (Aq<0), демографические (АМ<0) и социальноэкономические (AU<0) угрозы	Опережающее экстенсивное энергопотребление (АКУ)) с убывающей эффективностью производства (АфАО) и ухудшением качества
12	• Численность населения не убывает (ДМ > 0) • Совокупное производство товаров и услуг (полезная мощность) убывает (ДР < 0) • Суммарное потребление природных энергоресурсов не убывает (AN > 0) • Совокупный уровень жизни убывает (AU < 0) • Качество окружающей природной среды убывает (Aq < 0)	Энергосырьевой или экстенсивный	Экстенсивный рост за счет опережающего роста энергопотребления (ДХУ)), следствием которого могут быть экологические (Aq<0), демографические (ДМ<0) и социальноэкономические (AU<0) угрозы	Спад производства (АР<0), совокупного уровня жизни (AU<0) и ухудшение качества окружающей среды (Aq<0)

Мерой интеллектуальной возможности является неубывающий темп роста изменения эффективности использования полной мощности.

Интеллектуальная возможность равна I_w ( t ) = А ^ = А ^ + А ² ^ • t + А³ ^ • t ² > 0 . [L⁰ T⁰ ] (6)

Интеллектуальный капитал (I К ) – это накопленная на время t интеллектуальная возможность.

Интеллектуальный капитал равен I_K ( t ) = J A ^ dt . (7)

2. Компьютерное моделирование

Любая социально-экономическая система может быть представлена в виде динамической системы, имеющую структуру, показанную на рис.5:

---------------------------*"1 ---------------------------*■ у I :

N Ш p

G=N-P

Рис. 5. Закон сохранения потоков энергии

На входе системы – потоки энергии N, которые в сумме дают полное потребление. Система обладает способностью преобразовывать энергию с некоторой эффективностью использования ресурсов (ф = P/N), выдавая на выходе потоки полезной энергии P и теряя потоки G (G=N-P). В самом простом случае, динамическая система в каждый момент времени представима совокупностью 3-х параметров {N, P, φ}, либо {N, P, G}, каждый из которых описывается для момента времени ti состоянием S={Si, vi, ai, ji}, где Si – значение параметра в текущий момент времени i; vi, ai, ji соответственно скорость, ускорение, рывок в текущий момент времени i.

Вообще говоря, состояние параметра может быть описано так S={S i , ^f , ^f ,^ ? , — , ^? }-

Это означает, что если реальному физическому процессу можно поставить в соответствие некую гладкую математическую функцию времени S(t), то в каждый момент времени могут быть измерены или вычислены значение S(t { ), скорость S(t { ), ускорение S(t i )и более высокие производные по времени, которые и будут идентифицировать состояние процесса в текущий момент времени, характеризуя векторы направлений движения.

Реализована виртуальная онлайн-лаборатория, позволяющая автоматизировать процесс моделирования устойчивого социально-экономического развития систем разного уровня иерархии и доступная по адресу URL: http://lfs.ip64.net.

Рассмотрим применение компьютерного моделирования на конкретном примере для исследования устойчивости развития Российской Федерации, используя в качестве исходных данных таблицы суммарного потребления (ГВт), суммарного производства (ГВт) и www.rypravlenie.ru

том 11 № 1 (26), 2015, ст. 5

коэффициент использования ресурсов (безразмерная величина) по Российской Федерации за 2005-2011 год (Таблица 2).

Таблица 2. Базовые + дополнительные показатели по РФ, Японии и Казахстану

	2006	2007	2008	2009	2010	2011
	Численность населения(чел)
Российская Федерация	142500000,00	142100000,00	141950000,00	141910000,00	142389000,00	142960000,00
Япония	127756000,000	127770750,00	127704040,00	127557958,00	127450459,00	127817277,00
Республика Казахстан	15308085,000	15484192,000	15673999,000	16093481,000	16323287,000	16558676,000

а) – численность населения

	2006	2007	2008	2009	2010	2011
	Полная мощность (ТВт)
Российская Федерация	0,905	0,940	0,955	0,968	0,973	1,016
Япония	0,870	0,882	0,890	0,877	0,873	0,871
Республика Казахстан	0,063	0,059	0,064	0,066	0,073	0,080

б) – полная мощность

	2006	2007	2008	2009	2010	2011
	Полезная мощность (ТВт)
Российская Федерация	0,271	0,281	0,286	0,289	0,292	0,305
Япония	0,280	0,285	0,285	0,283	0,281	0,283
Республика Казахстан	0,019	0,017	0,019	0,019	0,021	0,023

в) – полезная мощность

	2006	2007		2008	2009	2010	2011
	Совокупный уровень		жизни
Российская Федерация	1,904	1,980		2,013	2,038	2,053	2,130
Япония	2,195	2,228		2,234	2,216	2,205	2,210
Республика Казахстан	1,215	1,121		1,204	1,207	1,315	1,413

г) – совокупный уровень жизни

Российская Федерация	2006	2007	2008	2009	2010	2011
	Качество среды
	-	0,963	0,983	0,986	0,997	0,958
Япония	-	0,987	0,988	1,018	1,003	1,006
Республика Казахстан	-	1,074	0,917	0,984	0,901	0,912

д) – совокупный уровень жизни

В результате получаем таблицу, в которой описано к какому сценарию развития соответствует объект управления, его характерные черты, а также его описание и негативные следствия. Результат работы автоматизированной системы проектирования показан на рис. 6.

том 11 № 1 (26), 2015, ст. 5

1	Объект	Тип	Динамика параметров	Сценарий	Характерные черты	Описание и
		2	• Численность населения не убывает (ДМ > 0)	Энергосырьевой	Экстенсивный рост за счет	Опережающий рост
г	Российская Федераци!		• Совокупное производство товаров и услуг (полезная мощность) не убывает (ДР > 0)	экстенсивный	опережающего роста энергопотребления (AN>0),	энергопотребления и, как следствие,
4			• Суммарное потребление природных энергоресурсов не убывает (AN > 0)		следствием которого могут быть экологические (Дд<0),	угроза энергоэкологическог
5			• Совокупный уровень жизни не убывает (AU > 0)		демографические (ДМ<0) и	о кризиса (Aq<0)
			• Качество окружающей природной среды убывает (Дд < 0)		социально-экономические (ди<0) угрозы
		1	• Численность населения не убывает (ДМ > 0)	Индустриально-	Интенсивный рост за счет	Индустриально-
	Республика Казахстан		• Совокупное производство товаров и услуг (полезная мощность) не убывает (ДР > 0)	иннов ационный	повышения эффективности производства (Дср>0),	инновационное развитие на фоне
g			• Суммарное потребление природных энергоресурсов не убывает (AN > 0)		возможными следствиями которого являются	роста базовых параметров
10			• Совокупный уровень жизни не убывает (AU > 0)		позитивные и негативные
			• Качество окружающей природной среды не убывает (Aq > 0)		изменения параметров
12		15	• Численность населения не убывает (ДМ > 0)	Индустриально-	Интенсивный рост за счет	Социально-
13	Япония		• Совокупное производство товаров и услуг (полезная мощность) убывает (ДР < 0)	иннов ационный	повышения эффективности производства (Дф>0),	экономический кризис на фоне
14			• Суммарное потребление природных энергоресурсов убывает (AN<0)		возможными следствиями которого являются	сохранения неубывающей
15			• Совокупный уровень жизни убывает (AU < 0)		позитивные и негативные	динамики
16			• Качество окружающей природной среды не убывает (Aq > 0)		изменения параметров	численности населения (ДМ>0) и

Рис. 6. Результат работы автоматизированной системы проектирования.

Режим «Идентификация существующего состояния»

Заключение

Впервые предложена математическая модель, удовлетворяющая базовым требованиям научного обеспечения устойчивого развития, сформулированным в начале работы.

Впервые:

1) аксиоматика математической модели строится на фундаментальных законах сохранения и изменения, выраженных на универсальном и едином языке пространственновременных величин.
2) параметры-формулизмы модели построены на фундаментальном законе сохранения мощности, выраженном на LT-языке.
3) правила вывода и критерии опережающего устойчивого развития выражены на фундаментальных законах изменения объектов управления.

Полученные новые результаты могут иметь большое практическое значение, так как дают возможность находить требуемые технологические решения и проектировать развитие систем различной природы на законной основе, рассматривая устойчивость развития как проекцию общих законов Природы.

Математическое и компьютерное моделирование устойчивого социальноэкономического развития на языке пространственно-временных величин с инвариантом мощность будет способствовать лучшему пониманию причин неустойчивости, глобальных и региональных кризисов и конфликтов, проблем перехода к устойчивому инновационному развитию, методов и прорывных инновационных технологий, повышающих результативность на всех уровнях управления.

Для обеспечения адекватной оценки ситуации, мониторинга и анализа должны применяться автоматизированные средства проектирования устойчивого развития, которые могут, в том числе, выступать в качестве экспертных систем. Это позволяет быстро и эффективно приобрести знания и понимание процессов, протекающих в сложных социальноэкономических системах.

Список литературы Компьютерное моделирование устойчивого социально-экономического развития России, Казахстана и Японии

Бартини Р.О. Некоторые соотношения между физическими константами // Доклады АН СССР: том 163, №4, 1965.-с. 861-864.
Бартини Р.О., Кузнецов П.Г. Множественность геометрий имножественностьфизик // Моделирование динамическихсистем.-Брянск, 1974.- с. 18-29.
Бауэр Э.С. Теоретическая биология.-СПб.: ООО «Росток», 2002. -352 с.
Большаков Б.Е. Наука устойчивого развития. Книга I. Введение.- М.: РАЕН, 2011.- 272 с.
EDN: QOOFOB
Большаков Б.Е. Система универсальных мер-законов в науке устойчивого развития. // Электронное научное издание «Устойчивое инновационное развитие: проектирование и управление»: том 7, вып. №4 (13) / 2011 [Электронный ресурс]. - Режим доступа: http://www.rypravlenie.ru/?p=1080, свободный.

Статья научная