Компьютерные технологии обучения методам Data Mining обработки данных
Автор: Ризаев Ильдус Султанович, Яхина Зухра Талгатовна, Мифтахутдинов Динар Ильдусович
Журнал: Образовательные технологии и общество @journal-ifets
Статья в выпуске: 2 т.18, 2015 года.
Бесплатный доступ
Рассматривается применение аналитической платформы Deductor для решения задач анализа данных в процессе обучения студентов магистерской подготовки. Показано, что для успешного анализа данных необходимо использовать методы OLAP и Data Mining. Рассмотрена архитектура и алгоритмы системы Deductor. На примере решения задачи классификации показано применение аналитической платформы.
Анализ данных, классификация, деревья решений
Короткий адрес: https://sciup.org/14062611
IDR: 14062611
Текст научной статьи Компьютерные технологии обучения методам Data Mining обработки данных
В настоящее время многие предприятия широко используют в своей повседневной деятельности сбор, хранение и обработку информации на основе концепции базы данных [1]. Системы подобного типа называются системами оперативной обработки транзакций или OLTP системами (Online Transaction Processing).
Часто возникает необходимость иметь доступ не только к текущим данным, но и к ранее накопленным (историческим) данным. С этой целью была разработана концепция хранилища данных (data warehouse). Кодд – основоположник реляционной модели баз данных – указал на недостатки традиционных баз данных, на невозможность объединять, просматривать и анализировать данные с точки зрения множественности измерений. Множественность измерений предполагает представление данных в виде многомерной модели. С концепцией многомерных данных тесно связана система оперативной аналитической обработки данных (OLAP-система). Аналитик опираясь на средства OLAP-системы выдвигает гипотезы, и опираясь на свой опыт и знания, анализирует данные. Оказывается, что новые знания можно получать и из ранее накопленных данных, которые подвергаются анализу. Добычей таких знаний из накопленных скрытых данных занимаются специальные программные средства, получившие название Data Mining, которые позволяют решать многие задачи, с которыми сталкивается аналитик. К таким задачам можно отнести: классификацию, кластеризацию, регрессию, поиск ассоциативных правил и прогнозирование [2-4].
В настоящее время существует большое количество инструментальных средств, позволяющих решать задачи Data Mining. Это такие системы, как SPSS, Statistica, SAS, также средства, использующие СУБД: MS SQL Server, Oracle и др.
На кафедре автоматизированных систем обработки информации и управления при Казанском национальном исследовательском техническом университете (КНИТУ-КАИ) ведется подготовка студентов магистрантов по направлению «Информационные системы и технологии». [7,8].
В вариативной части учебного плана магистерской подготовки включена дисциплина «Модели и методы интеллектуального анализа данных». Целью изучения дисциплины является освоение и применение моделей и методов интеллектуального анализа данных для принятия решений в сфере информационных технологий на базе средств Data Mining. Программа учебной дисциплины включает лекции, лабораторные занятия и курсовую работу. Для проведения лабораторных работ используется аналитическая платформа Deductor [5].
Аналитическая платформа Deductor
Целью лабораторного практикума является изучение и практическое освоение состава и назначения аналитической платформы Deductor (разработчик - компания BaseGroup Labs), а также систем подготовки исходных данных в текстовом формате, ввод данных и получение общих статистических значений. Структура системы Deductor представлена на рис.1.
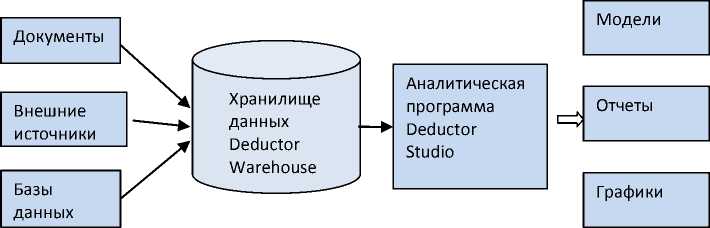
Рис.1. Архитектура системы Deductor
Deductor состоит из шести частей:
-
1 . Warehouse – хранилище данных, консолидирующее информацию из разных источников. В системе поддерживается концепция виртуальных хранилищ данных;
-
2 Studio – аналитическое приложение, позволяющее пройти все этапы
построения прикладного решения;
-
3 Viewer – рабочее место конечного пользователя, одно из средств тиражирования знаний;
-
4 Analytical Server – служба, обеспечивающая удаленную аналитическую обработку данных;
-
5 Client – клиент доступа к Deductor Server. Обеспечивает доступ к серверу из сторонних приложений и управление его работой;
-
6 Integration Server – веб-сервер, функционирующий поверх аналитической службы Deductor Analytical Server.
Существует три типа варианта поставки платформы Deductor:
Версия Enterprise предназначена для корпоративного использования.
Версия Professional предназначена для небольших компаний и однопользовательской работы.
Версия Academic предназначена для образовательных и обучающих целей. Ее функционал аналогичен версии Professional за исключением:
-
- отсутствует пакетный запуск сценариев, т.е. работа в программе может вестись только в интерактивном режиме ;
-
- отсутствует импорт из промышленных источников данных: 1С, СУБД, файлы MS Excel, Deductor Data File;
-
- некоторые другие возможности.
Источниками данных являются: хранилище данных; текстовые файлы с разделителями; пакет Microsoft Excel; СУБД Microsoft Access; Dbase и др.
(Учебная версия позволяет вводить только текстовые файлы .txt).
После получения выборки можно получить подробную статистику по ней, посмотреть - как выглядят данные на диаграммах и гистограммах.
Студенты, получив задание на выполнение лабораторной работы, должны учесть, что вся работа по анализу данных базируется на выполнении следующих действий: импорт данных; обработка данных; визуализация; экспорт данных.
Результаты каждого действия могут быть отображены в виде: OLAP куба; плоской таблицы; диаграммы, гистограммы; статистических данных; анализа по принципу «что-если»; графа нейросети; иерархической системы правил; и прочее.
Последовательность действий, которые необходимо провести для анализа данных, называется сценарием (рис.2).
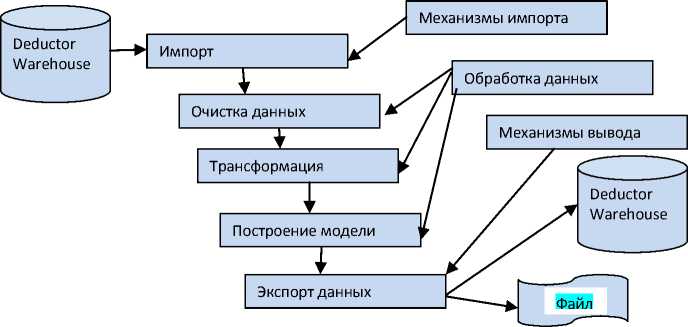
Рис.2. Сценарий Deductor Studio
Deductor Warehouse – многомерное хранилище данных, аккумулирующее всю необходимую для анализа предметной области информацию. На рис.3 представлено хранилище данных по продажам товаров. Вся информация в хранилище содержится в структурах типа «звезда».
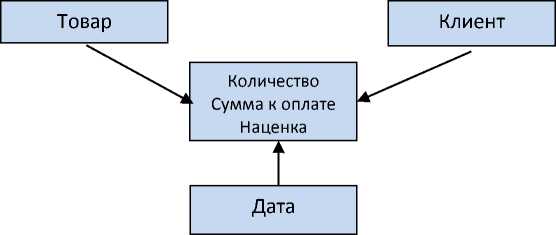
Рис.3. Хранилище данных «Продажа товаров»
Такая структура физически представляет реляционную базу данных (ROLAP). Каждая «звезда» называется процессом и описывает определенное действие. Поверх этой структуры имеется специальный слой, который преобразует реляционное представление в многомерное.
Основные алгоритмы Deductor Studio представлены на рис.4.
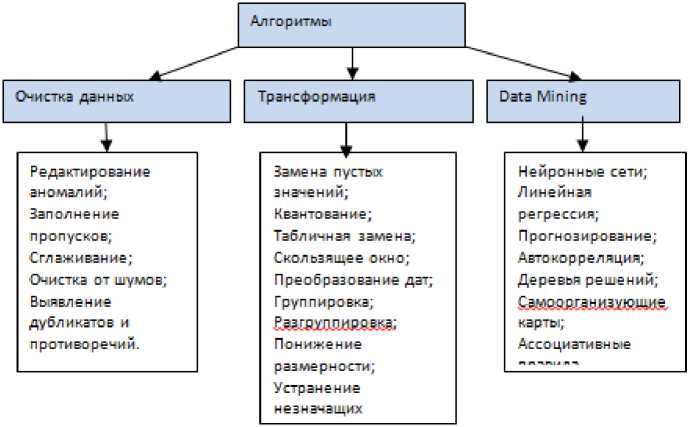
Рис. 4. Алгоритмы, используемые в Deductor
Data Mining – это не один метод, а совокупность большого числа различных методов обнаружения знаний. Базовыми методами являются:
Классификация – это установление зависимости дискретной выходной переменной от входных переменных.
Регрессия – это установление зависимости непрерывной выходной переменной от входных переменных.
Кластеризация – это группировка объектов (наблюдений, событий) на основе данных, описывающих свойства объектов.
Ассоциация – выявление закономерностей между связанными событиями.
При проведении лабораторных работ последовательно рассматриваются все перечисленные методы Data Mining, включающие как теоретическую, так и практическую части.
Ниже приведен пример решения задач обработки данных, связанный с классификацией объектов. На первом этапе студенты осваивают аналитические методы классификации, а на втором реализуют предложенный пример в среде Deductor.
Классификация
Решение задачи классификации сводится к определению класса объекта по его признакам, при этом множество классов, к которым может быть отнесен объект, известно заранее. С классификацией тесно связано понятие регрессии. Действительно, как классификационная, так и регрессионная модель находят закономерности между входными и выходными переменными. Если выходная переменная одна и является дискретной, то речь идет о задаче классификации, но если входные и выходные переменные модели непрерывные – задача регрессии.
В настоящее время существуют различные методы решения задач классификации. Все методы делят на статистические и методы машинного обучения.
Статистические методы
Линейная регрессия;
Логистическая регрессия;
Байесовская классификация.
Методы машинного обучения
Деревья решений;
Решающие правила;
Нейронные сети;
Метод k ближайших соседей и др.
Из перечисленных методов студентам предлагается провести классификацию на основе метода «Деревья решений» [6].
В основе данного метода лежит рекурсивное разбиение всего множества объектов на подмножества, ассоциируемые с классами. Мерой оценки разбиения на классы является чистота класса, что означает отсутствие в классе посторонних объектов (примесей). Существуют различные алгоритмы разбиения на классы, которые основываются на том, что разбиение производится по очереди по каждому входному атрибуту {A j } и проверяется степень увеличения чистоты разбиения.
Пусть задано множество объектов Q (A 1 , A 2 ,…,A n ), для которых определены классы {C 1 , C 2 ,…,C k }. Выбирается один из входных атрибутов A j, после чего данное множество разбивается на подмножества Q 1 , Q 2 ,…,Q n . Затем выбирается другой атрибут и проверяется разбивка на классы. Данная процедура будет повторяться до тех пор, пока подмножества не будут содержать объекты только одного класса. Надо иметь в виду, что процедура не является однозначной. В зависимости от последовательности применения атрибутов могут быть получены различные деревья решений. Задачей является получение наиболее идеального компактного дерева.
Эффективность разбиения можно оценить по чистоте полученных дочерних узлов. Существуют различные критерии разбиения. Наиболее популярными являются: индекс Gini, информационный критерий, ХИ-квадрат, метод Naïve Bayes и др.[2,6]. Оценка качества классификации выполняется с помощью следующих показателей: поддержка (support), достоверность (confidence).
Supp=Nкл/N, Conf=Nкл/Nус , где Nкл – число правильно классифицированных объектов, N – общее число объектов, Nус – число объектов, удовлетворяющих поставленному условию.
Индекс Gini представляет вероятность того, что случайным образом выбранные объекты в одном узле относятся к одному классу и определяется как сумма квадратов долей классов в узле. При информационном подходе необходимо определить значение энтропии в зависимости от долей классов в узле. Если все классы присутствуют в узле с равной вероятностью, то энтропия максимальна.
k
Info(Q) = -E Pj log2 Pj j=1
Пусть в некотором узле дерева решений S содержится множество Q, которое состоит из N объектов. В результате разбиения S были созданы k потомков Q 1 , Q 2 ,…,Q k , каждый из которых содержит число записей N 1 , N 2 ,…,N k . Для потомков пусть будет рассчитана энтропия - Info(Q j ). Тогда общая энтропия S составит:
Info(S) = N- Info®) + N^ Info(Q 2 ) + . + NMnfo®) ^N-Info® ) N N N 7=1 N
Для построения деревьев решений одним из проблемных вопросов является порядок выбора атрибутов. Для выбора порядка атрибутов воспользуемся алгоритмом ID3. В соответствии с этим алгоритмом необходимо использовать критерий, называемый приростом информации или уменьшением энтропии. Мера прироста информации задается следующим образом:
Gain(S)=Info(Q) – Info S (Q), где Info(Q) – энтропия множества Q до разбиения;
InfoS(Q) – энтропия после разбиения S.
Наилучшим является тот атрибут, который дает наибольший прирост информации Gain(S).
Пример учебной задачи
Рассмотрим построение дерева решений на примере кредитоспособности клиентов банка. Допустим, у нас имеется набор данных, содержащий 20 записей возможных кредиторов. Записи хранятся в таблице, отношение которой имеет вид (рис.4).
Табл(ФИО, Доход, Возраст, Недвижимость, Класс)
Банк производит классификацию кредитоспособности граждан в зависимости от трех атрибутов: дохода, возраста и наличия недвижимости. С помощью обучающей выборки граждане были разнесены по классам:
A – кредитоспособен, B – некредитоспособен.
В данной таблице 20 записей, 11 относятся к классу А¸ 9 – к классу B.
Энтропия множества Q составит:
Info (Q) = -{(11/ 20) log2 (11/20) + (9/ 20) log2 (9 /20)} = 0,9928
Supp(N кл /N)=11/20=0,55
На рис.5 приведены исходные данные инсталлированные в системе Deductor
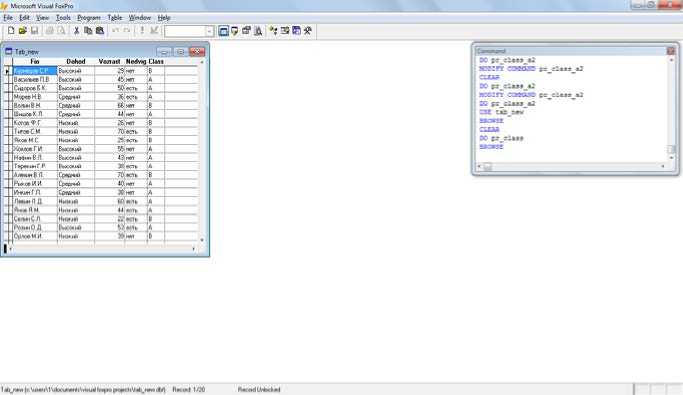
Рис.5. Таблица данных возможных кредиторов банка
В качестве начального атрибута возьмем Доход. Доход имеет три составляющих {Высокий, Средний, Низкий}. Тогда исходное множество будет разбито на три подмножества (рис.6). В подмножество Высокий вошло 7 записей из них в класс А попало 6 записей, в В - одна запись. В подмножество Средний - 6 записей, из которых класс А – 4, В -2. Подмножество Низкий – 7 записей, А – 2, В – 5.
Доход
Высокий
Кузнецов С. 29 нет В Васильев П. 45 нет А Сидоров Б. 50 есть А Хохлов Г. 55 нет А Волин В. 43 нет А Терехин Г. 38 есть А Родин О. 53 есть А
Средний
Морев Н. 36 есть А
Волин В. 66 нет В Шишов К. 44 нет А Алехин В. 70 есть В
Рыков И. 40 нет А Инкин Г. 38 нет А
Низкий
Котов Ф. 26 нет В
Титов С. 70 есть В
Яков М. 25 есть В
Левин Л. 60 есть А
Янов Я. 44 есть А Селин С. 22 есть В Орлов М. 39 нет В
Рис.6. Разбиение по атрибуту Доход для примера из таблицы на рис.4
Энтропия подмножества Высокий, Средний и Низкий соответственно составят: InfoQ) = ( 7 / 20 ) • (-( 6 / 7 ) • LOG( 6 / 7 )/LOG( 2 )-( 1 / 7 ) • LOG( 1 / 7 )/LOG( 2 )) = 0 , 207085 InfiQ ) = ( 6 / 20 ) • (-( 4 / 6 ) • LOG( 4 / 6 )/LOG( 2 )-( 2 / 6 ) • LOG( 2 / 6 )/LOG( 2 )) = 0 , 275489 InfoQJ = ( 7 / 20 ) • (-( 2 / 7 ) • LOG( 2 / 7 )/LOG( 2 )-( 5 / 7 ) • LOG( 5 / 7 )/LOG( 2 )) = 0 , 302092 Суммарная энтропия
Infos(Q) = Info(Qs i ) + Info(Qs 2 ) + Info(Qs з ) = 0 , 784666
Прирост информации после разбиения по атрибуту Доход составит: Gain(S)= 0,9928 – 0,7847=0,2081
Далее попробуем разбить по атрибуту Возраст.
В результате разбиения получили 2 подмножества (рис.6).
В подмножество Возраст 30-60 вошло 13 записей из них в класс А попало 12 записей, в В - одна запись. В подмножество Возраст вне (30-60) - 7 записей, все из которых вошли в класс В. Данное подмножество представляет чистый лист в котором содержатся объекты только одного класса.
Суммарная энтропия будет равна
Infos (Q) = Info ( Qs 2) + Info (Qs2) = 0,2543
Энтропия подмножества Высокий, Средний и Низкий соответственно составят:
Info(QSi) = ( 7 / 20 ) • (-( 6 / 7 ) • LOG( 6 / 7 )/LOG( 2 )-( 1 / 7 ) • LOG( 1 / 7 )/LOG( 2 )) = 0 , 207085
Info(QSi) = ( 6 / 20 ) • (-( 4 / 6 ) • LOG( 4 / 6 )/LOG( 2 )-( 2 / 6 ) • LOG( 2 / 6 )/LOG( 2 )) = 0 , 275489
Info(Q Sf = ( 7 / 20 ) • (-( 2 / 7 ) • LOG( 2 / 7 )/LOG( 2 )-( 5 / 7 ) • LOG( 5 / 7 )/LOG( 2 )) = 0 , 302092
Суммарная энтропия
Infos (Q) = Info (Qs,) + Info (Qs2) + Info (Qs3) = 0,784666Возраст
30 - 60 30> или >60
|
Васильев П. |
Высокий нет |
А |
|
Сидоров Б. |
Высокий есть |
А |
|
Морев Н. |
Средний есть |
А |
|
Шишов К. |
Средний нет |
А |
|
Хохлов Г. |
Высокий нет |
А |
|
Нафин В. |
Высокий нет |
А |
|
Теоехин Г. |
Высокий есть |
А |
|
Рыков И. |
Средний нет |
А |
|
Инкин Г. |
Средний нет |
А |
|
Левин Л. |
Низкий ест |
А |
|
Янов Я. |
Низкий есть А |
|
|
Розин О. |
Высокий есть А |
|
|
Орлов М. |
Низкий нет |
В |
|
Кузнецов С. Высокий |
нет |
В |
|
Волин В. Средний |
нет |
В |
|
Котов Ф. Низкий |
нет |
В |
|
Титов С. Низкий |
есть |
В |
|
Яков М. Низкий |
есть |
В |
|
Алехин В. Средний |
есть |
В |
|
Селин С. Низкий |
есть |
В |
Рис.7. Разбиение по атрибуту Возраст для примера из таблицы на рис.4
Прирост информации после разбиения по атрибуту Возраст составил:
Gain(S)= 0,9928 – 0,2543=0,7385
Далее проведем разбиение по атрибуту Недвижимость (рис.8).
Недвижимость
Есть
|
Сидоров Б. |
Высокий |
50 |
А |
|
Морев Н. |
Средний |
36 |
А |
|
Титов С. |
Низкий |
70 |
В |
|
Яков М. |
Низкий |
25 |
В |
|
Терехин Г. |
Высокий |
38 |
А |
|
Алехин В. |
Средний |
70 |
В |
|
Левин Л. |
Низкий |
60 |
А |
|
Янов Я. |
Низкий |
44 А |
|
|
Селин С. |
Низкий |
22 В |
|
|
Розин О. |
Высокий |
53 А |
|
Нет
|
Кузнецов С. Высокий |
29 В |
|
|
Васильев П. Высокий |
45 А |
|
|
Волин В. |
Средний |
66 В |
|
Шишов К. |
Средний |
44 А |
|
Котов Ф. |
Низкий |
26 В |
|
Хохлов Г. |
Высокий |
55 А |
|
Нафин В. |
Высокий |
43 А |
|
Рыков И. |
Средний |
40 А |
|
Инкин Г. |
Средний |
38 А |
|
Орлов М. |
Низкий |
39 В |
Рис.8. Разбиение по атрибуту Недвижимость
Суммарная энтропия и прирост информации составят:
Infos (Q) = Info ( Qs3) + Info ( Qs3) = 0,9709
Gain(S)= 0,9928 – 0,9709=0,0219
Прирост информации по последнему атрибуту является весьма низким.
Наилучшее разбиение произошло по атрибуту Возраст и поэтому он должен быть первым при разбиении в дереве решений. На рис.9 представлен оптимальный способ разбиения, необходимый для построения дерева решений на основе информационного подхода.
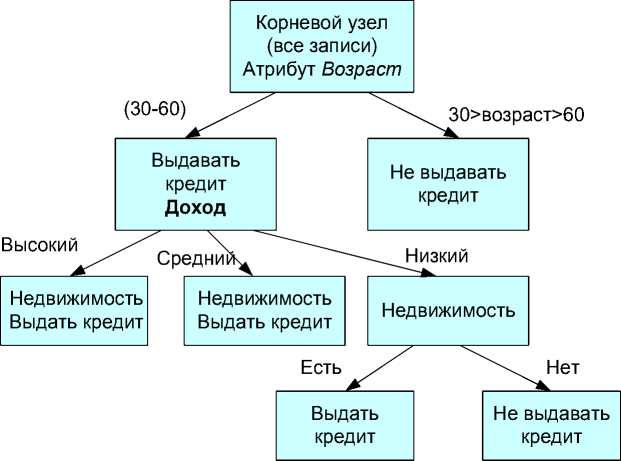
Рис.9. Полное дерево решений
Любое дерево решений подчиняется простому иерархическому правилу типа «Если А, то В». В данном случае можно сформулировать следующие правила:
Если {(Возраст от 30 до 60) и (Доход высокий или Доход средний)
ТО (Класс А)}
Если {(Возраст от 30 до 60) и (Доход низкий) и (Недвижимость есть)
ТО (Класс А)}
Если {(Возраст меньше 30 или больше 60) ТО (Класс В)}
После теоретической проработки материала, студенты проверяют результаты на практике, используя аналитическую платформу Deductor.
Работа в среде Deductor
Исходные данные должны быть подготовлены в среде Excel с сохранением в формате .txt. Например, подготовили таблицу «Кредитный риск» с атрибутами: Кредитный_риск(Код_клиента,Возраст,Доход,Имущество,Образование, КредРиск). Введенный файл будет воспроизведен в среде Deductor в виде таблицы (рис.10).
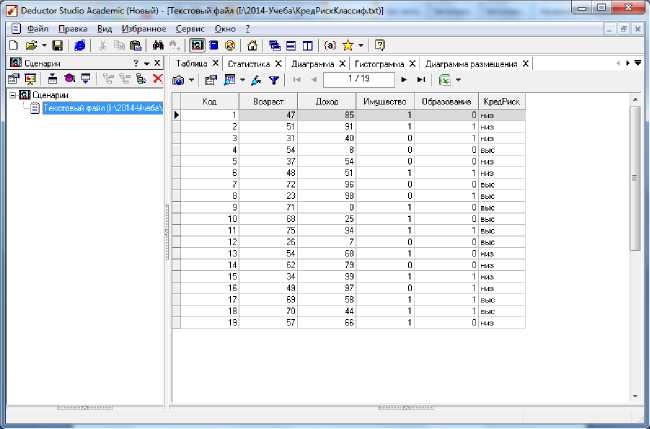
Рис.10. Таблица «Кредитный риск»
Далее можно проверить статистические данные (рис.11), где по каждому атрибуту выдается гистограмма и набор статистических данных.
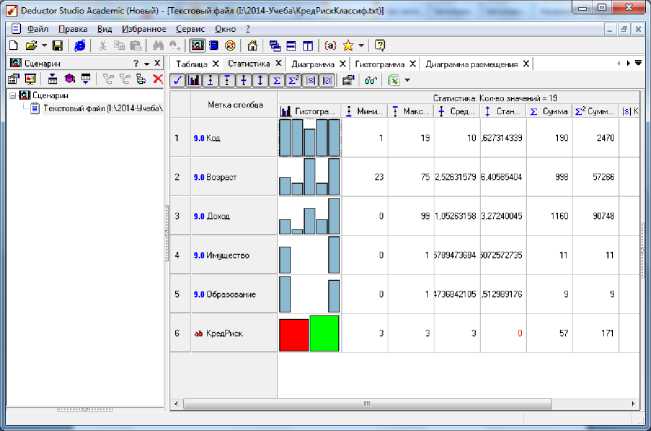
Рис.11. Статистические данные
На рис.12 можно увидеть зависимость кредитного риска в зависимости от дохода. Видно, что если доход низкий, то кредитный риск высокий и наоборот, при высоком доходе – кредитный риск низкий.
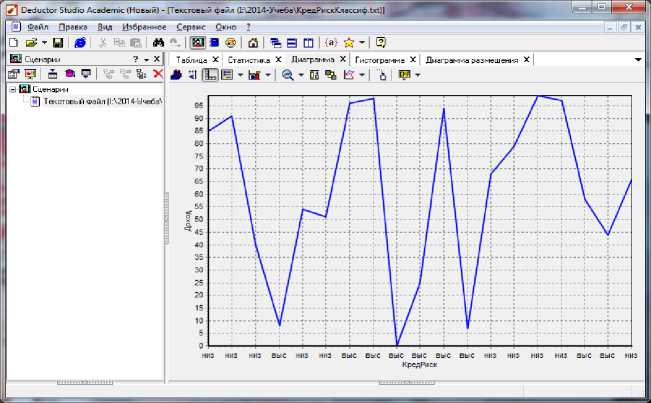
Рис.12. Зависимость кредитного риска от уровня дохода
На рис.13. показана зависимость кредитного риска в виде дерева решений
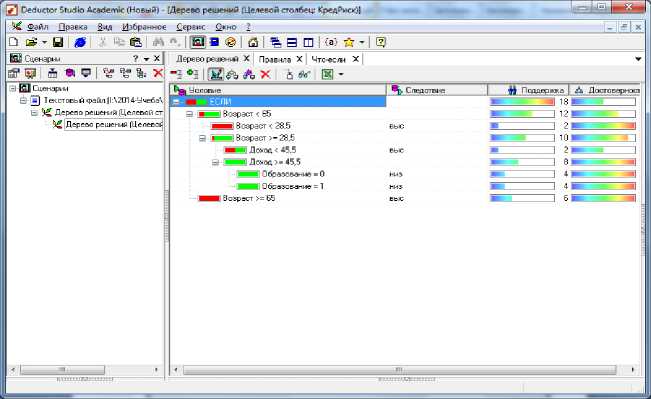
Рис.13. Дерево решений с визуализацией «Что-если»
Видно, что наибольшей поддержкой обладают возраст и доход. Образование является малозначимым атрибутом с весьма низкой поддержкой.
На рис.14 приведены пять правил определения кредитного риска.
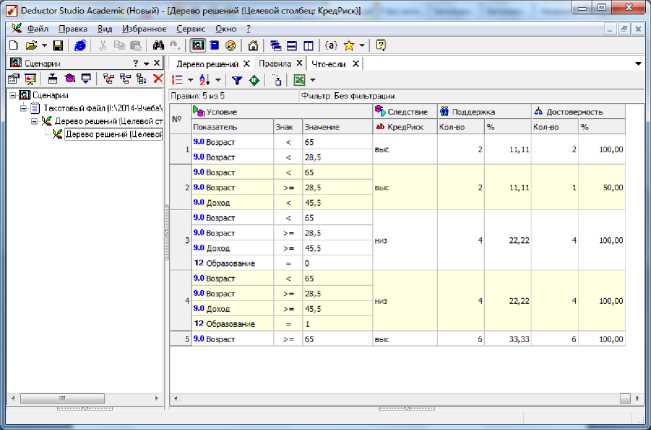
Рис.14. Правила дерева решений
Заключение
Пример показал простоту и удобство применения деревьев решений для классификации клиентов по кредитному риску. Мастер аналитической платформы Deductor предлагает широкие возможности по настройке процесса построения дерева решений. Алгоритм сам отсек несущественные факторы, выявил степень влияния тех или иных факторов на результат, описал при помощи формальных правил способ классификации, а также выдал информацию о достоверности и поддержке того или иного правила. Также были продемонстрированы широкие возможности визуализации построенного дерева.
Таким образом, на примере решения задачи классификации показаны хорошие возможности применения аналитической платформы Deductor.
Список литературы Компьютерные технологии обучения методам Data Mining обработки данных
- Ризаев И.С., Яхина З.Т. Базы данных: Учебное пособие -Казань: Изд-во Казан.гос.техн.ун-та, 2008 -с. 240
- Барсегян А.А. Технология анализа данных: Data Mining, Visual Mining, Text Mining, OLAP. -СПб.: БХВ-Петербург, 2008. -384 с.
- Data Mining for Business Application/Edited by L. Cao, Philip S. Yu, C. Zhang, H.Zhang. -Springer Science; Business Media, 2008
- Ризаев И.С., Рахал Я. Интеллектуальный анализ данных для поддержки принятия решений. -Казань: Изд-во МОиН РТ, 2011 -с. 172
- http://www.basegroup.ru/download/deductor.pdf
- Ризаев И.С., Осипова А.Л. Компьютерные технологии при решении задач классификации. Аналитическая механика, устойчивость и управление: Труды Х Международной Четаевской конференции. Т.4. Секция 4. Компьютерные технологии в образовании, управлении производством и тренажеры. Казань, 2012, Изд=во КГТУ с.243-249.
- Кирпичников А.П. Повышение аналитических возможностей баз данных./А.П.Кирпичников, А.Л.Осипова, И.С.Ризаев. Журнал Вестник Казанского Технологического ун-та, т.15, №3, 2012. -с.157-160.
- Яхина З.Т., Осипова А.Л., Ризаев И.С. Методология проектирования баз данных в процессе обучения./Журнал Образовательные технологии и общество (Educational Technology & Society)” -2012.-V.15.-№1-с.525-537. URL: http://ifets.ieee.org/russian/periodical/journal.html


