Компьютерный обучающий комплекс для персонала предприятий вагонного хозяйства с мультимедийными базами данных

ются оригинальные методы и алгоритмы идентификации и прогнозирования [4].

Ценность и значимость подобных комплексов многократно возрастает, если в них использовать алгоритмы идентификации и прогнозирования временных рядов производственных потоков.

Методы и алгоритмы идентификации и про- гнозирования квазистационарных временных процессов целесообразно использовать в компьютерных обучающих системах. Методы и алгоритмы идентификации, разработанные в [4 - 6], являются мощным инструментом в системах управления, передачи информации, изучении законов природы. Изучение временных процессов различной физической природы необходимо для построения краткосрочных и долгосрочных прогнозов, используемых для целесообразного рас- пределения материальных и технических ресурсов. Представлены методы и алгоритмы идентификации нелинейных динамических объектов в классе блочно-ориентированных моделей. Этот подход распространен на идентификацию пара- метров квазистационарных временных рядов, поскольку их можно генерировать с помощью линейного формирующего фильтра при подаче на его вход сигнала вида белый шум.

Измерительно-вычислительная система с корреляционно-спектральным идентификатором и блоком построения прогноза дана на рис. 1.

Для проведения дальнейших аналитических выкладок используются сигналы y (t) , Z i (t — Т^; Aty ) и Z 2 (t — Т 2 ; Atq ), которые имеют следующий вид:

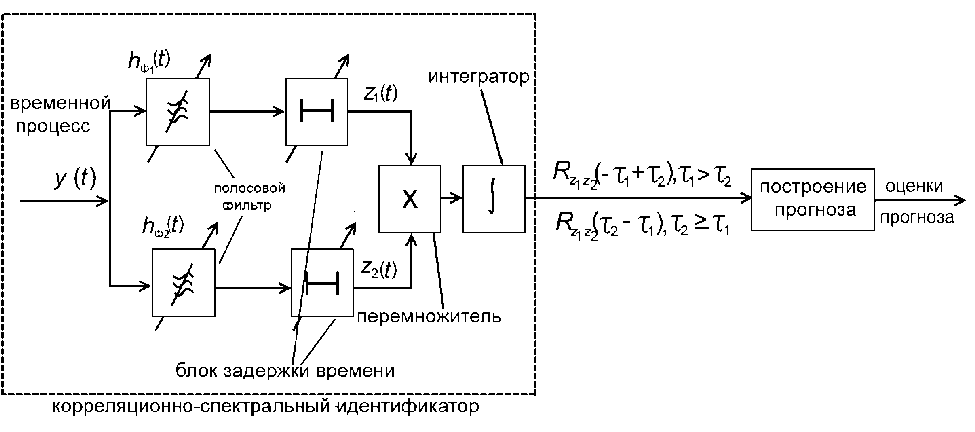
Рис. 1. Корреляционно-спектральный идентификатор с блоком прогнозирования.

то

y (t ) = J h фф (0) x (t — 9) d 9 ,

то z1 (t— ч;A t y )= J hф1 к)y(t — ч - цу; a t Y) d цу,

то

z 2 (t ^A’ A tq ) = J hф 2 (H q )У (t - T| — H q ; A tq ) d H q ,

дели квазистационарного временного процесса заключается в определении оценок qt k ⁽ i ), у^ i ) , n^i ), Q q^ и T qi ) в ПФ формирующего фильтра на квазистационарных участках A t i .

Получение алгоритмов процедуры корреляционно-спектральной идентификации временной последовательности основано на вычислении следующих корреляционных функций

где y, q g 1, l, hфф 0 -

импульсная переходная

R Z ₂ Z ₁ ^(т 2

-Т1 )=     - X

t 0 V2 ^Ч 1 ⁾

характеристика формирующего фильтра, h ф1 ( • ) и h ф 2 ( • ) — импульсные переходные характерис-

тики полосовых фильтров в корреляционно-спек-

t 0 ^-(т 2 ^-Т 1 ⁾

x Jz2(t-т2; Atа)z1 (t-т1; Atp)dt, t2 >t1,

тральном анализаторе.

X (t ) = G3(t) — белый

R Z ₂ Z ₁ ^{( T} 1 + ^T 2 ⁾

шум с неизвестным весом s, d( t ) – дельта функ-

t0 — (т1 — T2 )

X

ция; A t = t — t , i = 1, I , A t_x = A t ₂ = -• =A t_/ i             i +1             i

Обратное преобразование Лапласа от импульсной переходной функции линейного формирующего фильтра есть дробно-рациональная передаточная функция (ПФ) [1] вида:

t 0 ^-(т 1 ^-T 2 ⁾

X J z ₁ ( t -т ₁ ; A t c ) z ₂ ( t

-т ₂ ; A t_d ) dt , т ₁ >т ₂ ,

n( eq" $ +1) W фф'( $ )= k'i¹ -------------

П ^" $ + ^{1 ) 1}

q =¹

( i )             ⁽ i ⁾

где k , Q q и T q – соответственно масштабные коэффициенты и постоянные времени

где a , P , c , d g 1, l .

Уравнения (1) справедливы для случая, ког да tпп « A ti,где i = 1, l ,     - время пере- пп                         пп ходного процесса полосового фильтра. Также необходимо, чтобы 10 — (г2 — Т1 ) < Ati ,

Т2 > г1;  10 — (г1 — г2 ) < A ti, г1 > г2 и

формирующего фильтра, которые являются кусочно-непрерывными функциями времени (на квазистационарном участке эти функции не изменяются), m , n – порядки полиномов числителя и знаменателя ПФ. Задача идентификации мо-

i = 1, l.

Подставим в уравнения (1) выражения для сигналов y ( t ) , z 1 ( t — Т 1 ; A t ^ ) и z ₂ ( t — г ₂; A t q ) и получим следующие соотношения:

R Z 2 Z 1 ^(т2 ^{- T} ) =

= j-J h фф(⁶1; ^A a ^{) А} фф (⁶2 ; ^Ap ⁾ А ф2 (la ⁾ h ф, к ^)х о 0

^X R xx ^(t 2 ^{- T + 0}2 ^{- 0} +Ha ^- U _; ) d Ha d Hp ^d 61 ^d02 ,

R Z ₂ Z 1 t^{- (т}, ^{- T}2 ^)} =

= j^-j h фф ⁽⁶1; ^A c ⁾ А фф (6;; A t d ⁾ А ф 2 ⁽H c ⁾ ^ ⁽H d ^{) x} 0     0

X Rxx{- (t, - T2 ) + 61 - 62 + Hc - Hd }dHcdHdd01 d02 , где Rxx (т) = О25(т) - автокорреляционная функция белого шума с неизвестной О .

Порядки интегрирования интегральных уравнений (1) изменялись, поскольку:

то                            то j Афф (t)dt ^^ , j Аф1 (t)dt *то

О                      о то и j Аф 2 (t) dt *то

О

Для преобразования (3) также используем теорему Бореля о свертке:

то

R Z 2 z , ^(t 2 ^{t 1} ° ^ фИ ) '^ ф ^{( to} 2 ⁾ j ^CO>t' 0 U p ) /U ^X

-то xje...<-: - UpU p.to. , .=1)e-j^ Д8(ю-к02))+18(ю+ю,2))L -то                                                 <                                          0

то

RZ2Z, {-(т1 -т2)} = °2 j Аф1(Нc)dHc^i,^)x то

X j А фф ( to ) e        ^{H c} ' ■ ' ^{-0| )} e ' . 1 6 :'( U to¹

-то                                                             <

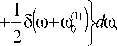
²к ^{( p)}L -/2)) K^(a)L '/^fcoslV//¹)!/

R Z 2 Z , V 2 ^Т 1 ⁾= ^{a А} фф ⁽ ^ 0 ^{) А} фф ⁽ ^ 0 ⁾ j ^COS( ^ 0 Ц р ) ^X

-то х/ pr\cf />) (2)A'T _T _ 11 _Ilf (P) f /7)(2) A //7)(2)AA/V//

^{X COS(} Ш о ^{( V} 2 ^V 1 ^Ц р Y фф ⁽ ^ 0 )/ ^ 0 )) ^{а Ц} р ,

²K ^{( d)}(z 'Z¹)) c ⁾fz'/¹)Исс₁чГл>(¹)/7

R Z 2 Z , ^{( ( V} 1 ^T 2 ) ⁾= ^{a А} фф ^{( Ш} 0 ^{) А} фф ^{( Ш} 0 ⁾ j ^{COS( Ш} 0 ^ц / ) ^X то

⁽¹⁾фт"                          ⁽ d ^{) (1)        (2)}

^X c^OS( Ш 0 ( Г 2 Т , ⁺ ^ c (V фф ^{( Ш} 0 )/ ^Ш 0 )) d ^ c .

Последние интегральные уравнения вычисляются на основе теоремы Бореля о свертке и фильтрующем свойстве 5 -функции

Структура и параметры чётного полосового фильтра в корреляционно-спектральном анализаторе должны быть выбраны такими, чтобы его импульсная переходная характеристика имела вид:

Аф (t ) = k ф. {exP (- ИД )cOS to И t }/ Ti , (i)

где to 0  - центральные частоты настройки фильтров, kфi – масштабные коэффициенты, Ti

RZ 2 Z, (т2 - Т1 ) = О 2 Кфр) (ш02) )афф* (ш02) )х хCOS{«.'((т2 -Т, (-Тфр)(ш02)УШ02) -^фф)(ш02)УШ02))}х х f 1 ^(ш*1’ - Шр) + 1 ^(шС) + Ш(2) )1;

2 ^{0 0} 2 ^{0 0}

Rz 2 z ,(- Т, + Т2) = О 2 Кфф И) )к:ф И))х хcos’m,2((-т, +т2 ! Тфф)(ш01)УШ01) +Тфф)(ш01)УШ01))}х хf 1 ^щ22 - Ш1)+1 ^Шо2 + Ш1){.

₂ 0      0 ₂ 0      0

– постоянные времени.

Предел lim Аф. (t) при Ti ^то и кф. jT( = 1 равен COS to0i)t при i = 1, 2.

^А ф i ^{( t )}

Предельные значения для

подставля-

ем в (2). Получаемые при этом интегралы вычис- ляются на основе фильтрующего свойства дельта функций:

то то

^RZ ₂ Z , ^(т 2 ^-т 1 ) = ° j ^- j ^А фф ^(б 1 ; ^A a ) ^А фф ^(б 2 ; ^А t p ) ^А ф1 ⁽ Н р ) ^Х

X cos( to 0 ²⁾ ( - ( T ₂ - t , + 0 ₂ -0 , -H p ))) d H_p d 0 , d 0 ₂, тото

^r z 2 z , ^{{- (t} i ^{- t} 2 ) ^} ° j - j ^а фф ⁽⁰ i ; ^A t c ) P ⁽⁰ 2 ; ^{A t}d ) ^А ф, ⁽ h d ) ^X

X cos( o) 0 ¹⁾ ( -t ₁ +t ₂ +0 , -0 ₂ +ц _c )) d h _c d 0 , d 0 ₂.

При выводе формул (4) учитывалось свойство эрмитовой симметрии для 5-функций от ча- стотных аргументов.

( 2 )        (1)

В случае равенства частот to 0 = to 0 = ω 0 имеем:

R Z 2 Z , ^{( г} 2 ^{- Г} 1 ⁾ = ^{О 2 К} ф ф ^{)( ш} 0 ^{) К} фф ^{)( ш} 0 ) ^{х х} c^{os { ш} 0 ^{( г} 2 ^{- Г} , ) ^{+ Т} ф;фф ^{)( ш} 0 ) ^{- Т} <ф ф ^{)( ш} 0 )^}, ^RZ 2 Z , ^{( - Г} 1 ^{+ Г} 2 ⁾ = ^{О 2 К} фф ^{)( ш} 0 ^{) К} фф ^{)( ш} 0 ) ^{Х х} c^{os { ш} 0 ^{( - Г} , ^{+ Г} 2 ) ^{- Т} фф ^{)( ш} 0 ) ^{+ Т} фф ^{)( ш} 0 ) ]:

Таким образом, получены выражения для взаимных корреляционных функций, в которые входят модули комплексных передаточных функций и фазовые характеристики формирующего фильтра. То есть, по критериям приведенным в [5, 6] можно осуществить идентификацию параметров формирующего фильтра.

В результате проведения процедур идентификации в общем случае для системы с постоянными сосредоточенными параметрами дискретная передаточная функция эквивалентной импульсной системы дается в виде:

K * ( 2 ) =

A + A1 z +...+ Al -1 zl1 + Alzl

• 1    + ВZ + ...+ B. _1 Zm-1 + BmZm

  l

  ∑ A k z^k

  к -0

  m

  1 + Z B . z‘ ,

  k -1

  
  

которая приводит к рекуррентному алгоритму: y *[ n ]= A Xn ]+...+ A^n - l ]- B J 1[ n -1]-...- В т У к [ n - m ] .

Следовательно, чтобы получить прогноз y ˆ t ( l ) , нужно выразить модель для процесса y _t+l в виде разностного уравнения и действовать с членами в правой части согласно следующим правилам:

• 1 . Члены y _t-j ( j = 0, 1, 2, ...), известные уже к моменту t , оставить без изменения.

• 2 . y _t+j ( j = 1, 2, ...), еще не известные, заменить их прогнозами y ˆ t ( j ) на момент t .

• 3 .Члены a _{t - j} ( j = 0, 1, 2, ...), уже известные, определить по y_t - j ^- y_t_j - 1⁽ l ) .

• 4 .Члены a _t+j ( j = 1, 2, ...), еще не известные, заменить нулями.

Основная проблема в задаче анализа и прогнозирования заключается в построение модели, адекватно отражающей динамику временных рядов производственных потоков.

Компьютерный обучающий комплекс для технического и управленческого персонала предприятий вагонной дирекции был создан как платформа для апробации и внедрения в технологический процесс аппарата идентификации и построения прогнозов изменчивости временных последовательностей производственных потоков. При реализации процедур идентификации и прогнозирования осуществляется циклическое сканирование исследуемого процесса для уточнения модели временного ряда

Моделирование (имитация) производственного процесса, ситуаций окажет существенную помощь при изучении персоналом технологии осмотра вагонов. Поэтому разработка программных комплексов для целей дистанционного обучения и приобретения тренинговых навыков является актуальной [1, 2, 3]. В программный комплекс-тренажер включены все блоки, позиции, устройства и процедуры, соответствующие технологической карте осмотра вагонов, утвержденной ОАО “РЖД”.

Создание базы данных неисправностей вагонов, возникающих в процессе эксплуатации, имеет актуальное значение. Её дальнейшая обработка статистическими и корреляционно-спектральными методами и методами прогнозирования предназначена для формирования правильных управленческих решений по использованию материальных и трудовых ресурсов.

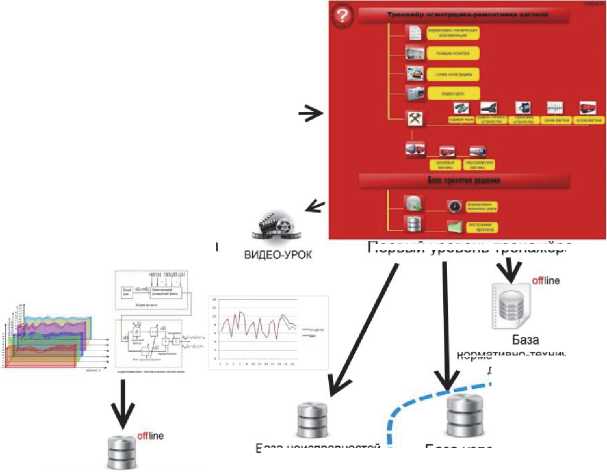
На рис. 2 показаны технологический алгоритм

Второй уровень -для инженерного персонала

База данных, используемых а модуле прогнозирования

База узлов деталей вагонов

База неисправностей । и дефектов

Модуль прогнозирования Настройка чётного фильтра

online загрузка данных S,

Online-регистрация дефекта в базе с помощью фотоустройства последующее развитие тренажера

ПОЗИЦИИ ОСМОТРА

Первый уровень тренажёра нормативно-техническая документации

Рис. 2. Взаимодействие и содержание модулей компьютерного комплекса.

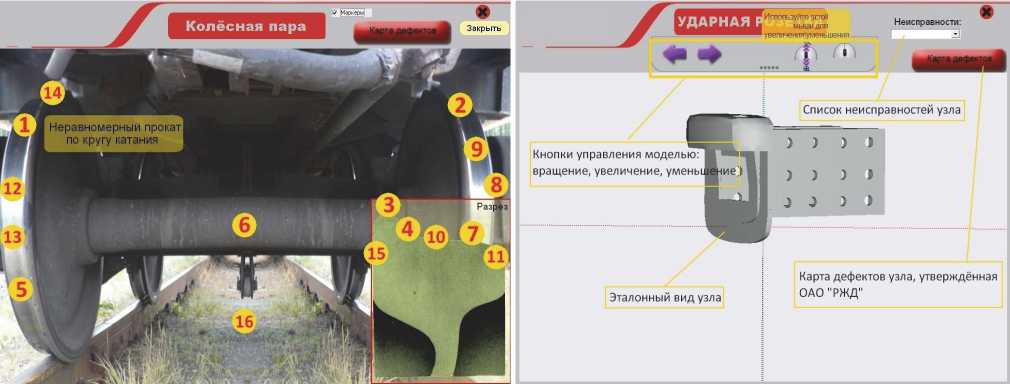
Рис. 3. Интерфейс манипулирования узлами вагонов. Интерфейс дефектов.

ПОЗИЦИИ ОСМОТРА

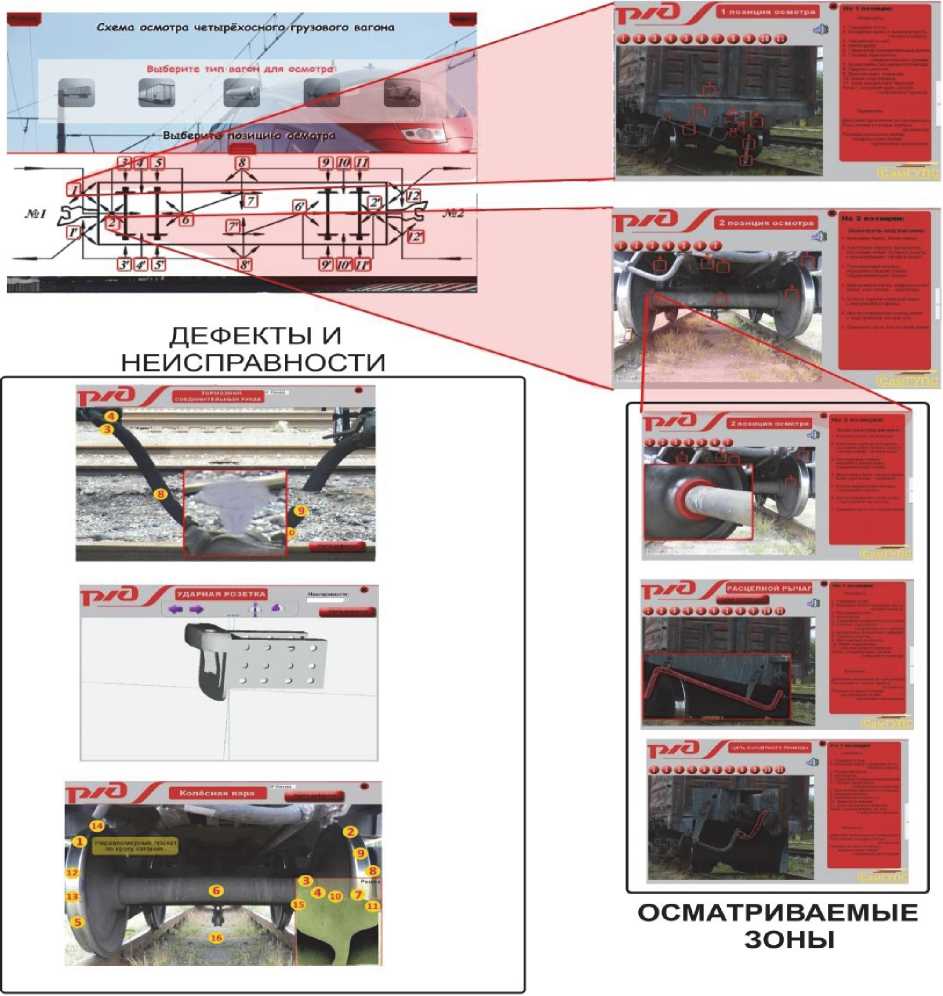
Рис. 4. Схема функционирования программных модулей.

реализации комплекса, интерфейс структуры тренажера, алгоритм функционирования программных модулей, модуль анализа временных рядов с корреляционно-спектральным анализатором.

Основным блоком является модуль осмотра по 12-ти позициям. Интерфейсы каждой позиции осмотра имеют две зоны: 1) – изображение реального вагона с соответствующего ракурса с активными маркерами; 2) - текстовое поле с перечнем узлов осмотра, которое можно при необходимости свернуть или развернуть. Модуль “Диагностика узлов вагона” содержит подмодули основных узлов вагона (ходовая часть, ударно-тяговые устройства, тормозное оборудование, рама вагона, кузов вагона), базу видов неисправностей, подпрограмму - инструменты и приспособления.

Все мультимедийные объекты хранятся в зашифрованном виде в базах данных MS Access.

Исходя из целесообразности, диагностируемые узлы представлены либо видео файлом, либо в 3D формате. В блоке “Диагностика узлов вагона” в меню “Ходовая часть” применен следующий алгоритм обучения и взаимодействия с программой: типовые виды колесных пар, интерактивная модель с возможностью манипуляции объектом (рис. 3), окно с методикой осмотра и выявления неисправностей, файл типовых неисправностей на виртуальной модели, модуль манипуляции инструментами и шаблонами, файл видео-сюжет с неисправностями и дефектами на реальном объекте, технологическая карта с неисправностями. Каждый блок завершается тестовой работой.

Программный комплекс, созданный в программной среде Delphi7, может быть использован для обучения эксплуатационного и ремонтного персонала, технологов ОАО “РЖД”; в образовательном процессе для студентов.

Ценность и функциональность тренажера существенно повышается, за счет включения модуля по сбору, хранению и обработке информации по дефек- там и неисправностям. Массивы данных обрабатываются методами идентификации с целью получения моделей для дальнейшего использования их в прогнозах [4]. Блок принятия решения предназначен для формирования рекомендаций и оптимальных управленческих шагов и решений по оптимизации материальных и трудовых ресурсов. Эти блоки могут быть использованы при проведении тренинговых мероприятий с персоналом управленческого звена.