Компьютерный расчет оптических систем в области аберраций высших порядков

Расчет в области аберраций высших порядков наиболее эффективен в том случае, когда силовыми элементами оптической системы являются градиентные и дифракционные линзы. Это обусловлено в основном двумя причинами. Во-первых, аберрационное разложение такой системы при надлежащем выборе исходной схемы сходится достаточно быстро, благодаря чему устранение аберраций каждого последующего порядка приводит к ощутимому улучшению оптических характеристик.

Во-вторых, градиентные и дифракционные линзы обеспечивают возможность селективной коррекции аберраций различных порядков. Действительно, в случае радиально-градиентной линзы (показатель преломления которой от

n (р ) = Е npp2 p

Р = 0

где р - расстояние от оси линзы) коэффициенты n _p влияют на аберрации, начиная только с (2 p +1)-го порядка.

В случае дифракционной линзы (фокусирующие и аберрационные свойства которой определяются законом изменения пространственной частоты ее структуры

Q ( р ) = (1/ А )

от

1 = 1

где Ф _о - оптическая сила линзы на длине волны А , ) коэффициенты b 2 1 +1 влияют на аберрации, начиная только с (2 p +1)-го порядка.

Известные методики вычисления аберраций третьего и пятого порядков оптических систем, состоящих из градиентных линз [1,2] основываются на использовании теории квазиинвариантов [3]. Это позволяет достаточно легко распространить указанные методики и на системы с дифракционными элементами, для чего необходимо лишь получить в приближении соответствующего порядка малости вклад в приращение квазиинварианта, вносимый дифракционной линзой [4].

Однако, с точки зрения широты функциональных возможностей больший интерес, на наш взгляд, представляет путь получения аберрационных коэффициентов по диаграмме рассеяния псевдолучей, ход которых через оптическую систему рассчитывается в приближении заданного порядка малости. В этом случае переход к все более и более высоким аберрационным порядкам существенно проще, а процесс вычислений легко алгоритмизируется. Более того, использование псевдолучей кроме вычисления аберрационных коэффициентов различных порядков позволяет осуществить минимизацию суммарной аберрации раздельно в каждом порядке и, наконец, минимизировать остаточную аберрацию того или иного типа путем взаимного балансирования ее составляющих различных порядков.

Расчет хода как реального, так и псевдолуча через оптическую систему, включающую элементы различных типов, основывается на использовании в той или иной последовательности формул расчета хода луча через отдельные ее элементы. Такие формулы по известным параметрам луча на входе в элемент (входным параметрам) позволяют определить параметры луча на выходе из него (выходные параметры). В дальнейшем совместим ось оптической системы с осью OZ, а в качестве лучевых параметров воспользуемся парой векторов р и ц , определяющих луч в его точке пересечения с плоскостью, нормальной к оси системы и отстоящей от начала координат на некотором расстоянии z .

Вектор р определяет точку пересечения и имеет составляющие [ x ( z ), y ( z ), 0]. Вектор ц определяет наклон луча и его составляющие [ s x ( z ), s y ( z ), 0) связаны с направляющими косинусами луча ( a x , а y , а z ) соотношениями s x = a x / а z , s y = a y / a z .

Для того, чтобы получить формулы расчета хода псевдолуча через оптический элемент того или иного типа, необходимо точные формулы расчета хода луча через элемент привести к виду, удобному для их последующего разложения в ряды по степеням входных параметров луча.

В результате после разложения и соответствующей группировки параметры луча на выходе из элемента будут описываться степенными рядами, состоящими из слагаемых различных порядков малости относительно параметров луча на входе в этот элемент. Ограничивая ряды конечным числом слагаемых, получим выходные параметры псевдолуча, вычисленные в требуемом приближении.

Получение необходимых формул начнем с преломления луча на сферической поверхности, имеющей кривизну c и являющейся поверхностью раздела двух неоднородных сред с показателями преломления n и n ’.

В соответствии с законом Снеллиуса-Декарта направляющие векторы падающего и преломленного лучей а и а ’ связаны соотношением [5]

a' = va - AN, (3) где N - направляющий вектор нормали к преломляющей поверхности в точке падения луча, v = n/n',

A = - v ( N • a ) + ^ 1 - v ² [ 1 - ( Na ) ² ]

^       (4)

Вводя в уравнения (3), (4) векторы £ и р , их нетрудно привести к виду [6], удобному для разложения по степеням входных параметров луча

e' = B (vaz e + cA r)

В уравнении (5)

a z = V V1 + 2 w

B = 1/ ( va z - A a] 1 - 2 c ² u

A = -v D + ^ 1 - v ² ( 1 - D ²)

D = a z (V 1 - c ² u - cv ) to                       / to

v=E np(2 u) p /Z nq( 2 u)q p=0            / q=0

где величины u, v и w являются инвариантами вращения и определяются с помощью соотношений

u = r ², v = ( r e ) , w = e ² /2                  (7)

Разлагая выражения (6) в ряды по степеням

трех инвариантов вращения, подставляя эти разложения в уравнение (5) и группируя после перемножения члены, имеющие одинаковый порядок малости, получим выходной параметр луча ( £ ‘ ) в виде

суммы слагаемых первого, третьего, пятого и т.д.

порядков малости относительно входных параметров (модулей векторов р и £ ):

e ' = e '^{( 1 )} + e '^{( 3 )}+ e '^{( 5 )} +                                (8)

Аналогичные соотношения могут быть получены и для дифракционной линзы. Направляющие косинусы падающего и дифрагировавшего лучей при дифракции на линзе, структура которой имеет

пространственную частоту и выполнена на плоской

подложке, связаны соотношениями [7]

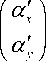
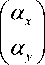
тЛП

Р

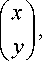
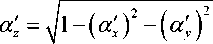
где т - порядок дифракции, X - длина падающей световой волны, x и у - координаты точки пересечения луча с плоскостью линзы.

Подставляя в первое из соотношений (9) пространственную частоту (2) и вновь вводя векторы р, £ перейдем от соотношений (9) к уравнению вида e' = Q (aze + тцуг)                  (10)

где

Ц = ^

to

V = ^Ф 0 ⁺ Z ^b 21 + 1 ( ² u )^Z 1 = 1 а величина

Q = 1/ a Z = V 1 + (O 2                   (12)

Из структуры соотношений (10)-(12) видно, что после разложения в степенные ряды уравнение (10) приводится к виду (8), а выражение (12) - к ряду, содержащему величины нулевого и четного порядков:

Q = Q ^{( 0 )} + Q ^{( 2 )} + Q ⁽⁴⁾+                    (13)

где Q ⁽⁰⁾=1.

Путь использования формул (10)-(13) для вычисления компонент различного порядка малости вектора £ ’ очевиден. По известному определяется компонента £ ’ ⁽¹⁾, зная последнюю находится Q ⁽²⁾, позволяющая определить компоненту £ ’ ⁽³⁾ и т.д.

Обратимся теперь к расчету хода псевдолуча через среду, ограниченную к-й и (к+ 1)-й поверхностями раздела. Зададим луч на входе в среду (после преломления на к-й поверхности) векторами рк и £к, а на выходе из среды [в точке падения на (к+1)-ю поверхность, но до преломления на ней]-векторами рк+1 и £к+1. Если среда является однородной, то наклон луча при прохождении среды не меняется (£к+1=£к), а векторы рк+1 и рк связаны между собой уравнением гк+1 = гк + zk, к+1e к                             (14)

Здесь zк,к+1 - координата точки выхода луча из среды в системе координат, начало которой лежит в плоскости перпендикулярной оси OZ и проходящей через точку входа луча в среду. Следовательно zk, к+1 = dk + zk+1 - zk                         (15)

где d_k - расстояние между вершинами к -й и ( к +1)-й поверхностями, z_{k +1} - координата точки пересечения луча с к -й поверхностью в системе координат, связанной с вершиной этой поверхности, и, аналогично, z_{k +1} - координата точки пересечения луча с ( к+ 1)-й поверхностью в системе координат, связанной с вершиной ( к+ 1)-й поверхности.

Координаты z_k и z_{k +1} можно нетрудно найти, воспользовавшись уравнением сферической поверхности [8]:

z = (bJ1-c2P) jc . (16)

Выражения (14)-(16) являются основой для получения формул расчета хода псевдолуча через однородную среду.

Структура выражений (15) и (16) такова, что координата zk,k+1 после разложения в ряд приводится к виду (13) с z^k+1 = dk. Это, как и в случае дифракционной линзы, позволяет организовать на основе метода последовательных приближений процесс вычисления компонент различного порядка малости вектора рk+1, и тем самым определить точку выхода луча из среды в приближении заданного порядка.

Если среда неоднородная и радиально-градиент- ная, то траектория луча в ней в декартовых координатах описывается системой двух скалярных дифференциальных уравнений [9]:

d 2 x	22 , ( dx ]    ( dy ]	d n л
n --Г -	1 + 1 — 1 +1 ~ 1	— = 0
dz2	( dz J ( dz J	d x
d 2 y	22 , f dx । f dy ।	d n л
n -	1 + 1 — 1 +1 ~ 1	— = 0
dz 2	( dz J ( dz J	9 y

С использованием же вектора эта система приводится к одному векторному дифференциальному уравнению d2r dz2

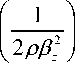
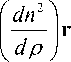
где в _z - оптический направляющий косинус луча относительно оси Oz , являющийся для радиальноградиентной среды инвариантом [10].

Дифференциальное уравнение (18) можно привести к виду, удобному для интегрирования, выпол- нив замену переменных и использовав представление показателя преломления, отличное от (1). Неза- висимую переменную z заменим на e = n йТ1zМ

а векторные параметры луча р и 8 - на векторы где ti = 72 (ni (in о

Профиль показателя преломления представим в виде где

1 1 при n 1 >  0

sgn ( n 1 ) = 1 0 при n 1 = 0

[- 1 при n 1 <  0

а коэффициенты т ₂ , т ₃ ,... в соответствии с выражением (1) равны

1 f 1 т= n0n2 n12

n 0

^{Т 3}     4 n 2

n ₀ n ₃

2 + n1

После указанной замены переменных дифференциальное уравнение (18) приводится виду d2R

de где

В приближении первого порядка малости (параксиальном приближении) правая часть уравнения (25) равна нулю. В этом случае уравнение сводится к хорошо известному однородному линейному дифференциальному уравнению второго порядка с постоянными коэффициентами, решение которого [8]

где

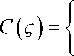
che cos e

ch e

sin e

при n 1 >  0

при n 1 <  0

при n 1 >  0

при n 1 <  0

R k и E k - векторные параметры луча на входе в среду.

Компоненты более высокого порядка параметров луча внутри среды можно получить методом последовательных приближений. В этом случае решение дифференциального уравнения (25) сводится к вычислению интегралов [11]:

e              e

Входящие в выражения (29) интегралы были вычислены в приближении пятого порядка в работах [11,12] и в приближении седьмого порядка в работе [13]. Используя результаты этих работ, а также следуя пути, предложенному выше для определения точки выхода псевдолуча из однородной среды, определяют компоненты различных порядков малости векторов R k +1 и E k +1 на выходе из неоднородной среды. После того как найдены эти компоненты, с помощью соотношений (20) осуществляют обратный переход к векторам р _{k +1} и 8 _{k +1} , т.е. тем самым находят компоненты различных порядков выходных параметров псевдолуча из радиально-градиентной среды, ограниченной сферическими поверхностями.