Комплекс испытаний для определения влияния напряженного состояния на прочность металлополимерных адгезионных соединений

ВЕСТНИК ПНИПУ. МЕХАНИКА № 5, 2024PNRPU MECHANICS BULLETIN

При создании современной техники наблюдается устойчивая тенденция к увеличению внешних механических, термических и др. нагрузок при необходимости сохранять работоспособность и живучесть в экстремальных условиях эксплуатации, в том числе и при внештатных ситуациях. Наглядно это проявляется в развитии аэрокосмической техники, конструкций и устройств, предназначенных для работы в арктических условиях. Например, температурные напряжения, возникающие вследствие большой разницы температур на солнечной и теневой сторонах конструкций в районах Крайнего Севера и Антарктиды, приводят к циклическим температурным деформациям. При этом могут существенно повреждаться защитные покрытия и клеевые соединения, материал которых подвергается дополнительным нагрузкам из-за различия коэффициентов термического расширения покрытия и металлической основы. Монтажные, а также снеговые и ветровые нагрузки на конструкции приводят к возникновению сложного напряженного состояния в защитных покрытиях и клеевых соединениях, усугубляемого действием отрицательных температур.

Использование металлополимерных соединений является перспективным направлением создания композиционных материалов, сотовых и слоистых силовых конструкций, сочетающих высокую прочность и малый вес. В качестве связующего, обеспечивающего необходимую адгезионную связь, обычно используются тер- мореактивные полимерные адгезивные материалы, которые, как и другие конструкционные материалы, должны обеспечивать прочность соединения, достаточную для его надежной эксплуатации в составе конструкции.

В настоящее время проектирование композиционных материалов обычно осуществляется с использованием систем инженерного анализа ANSYS, ABAQUS, FIDESYS и др., которые предполагают проведение глобальных прочностных расчетов элементов конструкций и их соединений, как правило, находящихся в условиях сложного напряженно-деформированного состояния в процессе эксплуатации. Но во встроенных базах данных этих программных комплексов практически отсутствуют сведения о механических свойствах полимерных адгезивов. В основном в технической документации на адгезивные материалы присутствуют сведения только о пределе прочности на сдвиг (реже на отрыв) и, как правило, при комнатной температуре. В отличие от металлических материалов, для которых обычно известны прочностные свойства в широком диапазоне температур, для материалов адгезивных покрытий подобная информация крайне ограничена. Отсутствие этих данных не позволяет производить полноценные проектные прочностные расчеты для покрытий и клеевых соединений в составе конструкций и механизмов для реальных условий эксплуатации. Таким образом, весьма актуальным является определение возможностей адгезивов сопротивляться разрушению в условиях сложного напряженного состояния и температурного воздействия.

В технической и научной литературе описано большое количество испытаний на прочность адгезионных соединений. По мнению авторов обзора [1], их число превышает 200. В большей степени речь идет об испытаниях, моделирующих условия работы конкретных соединений в заданных условиях. Например, испытания на раздир и сдвиг растяжением соединений с покрытиями и листовых материалов [2], выдергивание волокна из связующего [3] и др. Перенос результатов на другие условия нагружения и на другие соединения, как правило, невозможен. Изучению нарушения целостности соединений, образования и развития разрушающих трещин под действием критических силовых нагрузок, определяемых внешними параметрами (температура, скорость и характер приложения нагрузки), посвящено большое количество исследований в области механики (см. например, обзоры [4–9]). При этом в настоящее время отсутствуют сложившиеся представления о том, по каким критериям следует оценивать прочность адгезионных соединений и какие характеристики напряженного состояния при этом использовать. В инженерных расчётах зачастую применяют силовые критерии, основанные на использовании традиционных теорий прочности твердых тел, а также критерии, специализированные для решения задач адгезионной прочности (см. обзоры [10–12]). При прогнозировании разрушения адгезионных соединений с помощью силовых критериев имеется ряд существенных ограничений, связанных с невозможностью их использования в краевых областях с сингулярностью напряжений, также с их нечувствительностью к толщине слоя адгезива [12]. Кроме того, силовые критерии не учитывают влияние истории изменения напряженно-деформированного состояния на разрушение адгезионного соединения.

Важным шагом в прогнозировании прочности адгезионных соединений явилась разработка моделей когезионной зоны ( CZM – Cohesive Zone Model ), в соответствии с которыми распространению трещины предшествует развитие повреждений материала перед ее вершиной. При этом продвижение трещины происходит при достижении поврежденности критического уровня. Моделям CZM посвящен специальный выпуск журнала Engineering Fracture Mechanics (2003), а также более поздние обзоры в работах [13; 14]. В качестве определяющего параметра моделей CZM обычно используют скорость высвобождения энергии G , рассчитываемую как работу, затраченную на образование единицы свободной поверхности при распространении трещины [14]. Для экспериментального определения G с и идентификации моделей по диаграммам traction – separation проводят различные испытания в условиях отрыва ( G с I ), сдвига ( G с II ) и поперечного сдвига ( G с III ), в том числе регламентируемые стандартом ASTM D5528. Использование моделей CZM позволяет решать важные задачи сохранения живучести адгезионного соединения в случае наличия или образования в нем трещин.

При проектировании адгезионного соединения также важно определить уровень допускаемых механических нагрузок, превышение которого может привести к инициированию начальных несплошностей на границе соединения и, как следствие, к возникновению и распространению трещин, а затем и к разрушению соединения при дальнейшем нагружении [15; 16]. В этом смысле эффективным показателем может являться предельная величина работы/энергии, затрачиваемой внешними силами на образование локального нарушения сплошности в наиболее нагруженных и опасных участках соединения. Критерии, основанные на использовании энергии деформации, учитывают все компоненты тензоров напряжений и деформации. Поэтому они в большей степени подходят в качестве критерия начала разрушения, чем стандартные силовые и деформационные критерии. Кроме того, в отличие от скорости высвобождения энергии, работа обладает свойством кумулятивности, что дает принципиальную возможность учитывать влияние истории изменения условий деформирования на разрушение адгезионного соединения. Опыт использования этого параметра ограниченно описан в научно-технической литературе. Так, в статье [17] в качестве критерия разрушения использовали плотность энергии деформации, усредненную по деформируемому объему адгезива. Авторы проводили испытания только для растяжения листовых образцов, соединенных внахлест, поэтому ими не изучалась зависимость предельной плотности энергии деформации при разрушении от характеристик напряженного состояния.

Также следует отметить, что с позиций экспериментальной механики удобнее иметь ограниченное количество видов испытаний и форм образцов, но при этом изменять условия нагружения этих образцов так, чтобы в наиболее широком диапазоне варьировать напряженное состояние. Проведенный анализ известных методов испытаний прочности адгезионных соединений и собственный опыт авторов показывают, что на роль таких видов испытаний могут претендовать растяжение модифицированных образцов Аркана, трехточечный изгиб многослойных образцов, поперечное сжатие склеенных цилиндрических образцов (в англоязычной литературе Brazil-nut-sandwich ), в дальнейшем BNS -образцов.

Цель исследований – анализ особенностей проведения этих испытаний и обработки их результатов, что позволит получать единые зависимости для описания адгезионной прочности в широком диапазоне напряженного состояния.

1.    Методики проведения испытаний 1.1.    Модифицированные образцы Аркана

Образцы, впоследствии названные модифицированными образцами Аркана, были предложены в работе [18] и затем усовершенствованы авторами исследова- ний [19]. Они предназначены для определения прочности клеевых соединений при нагружении по схеме «растяжение/сжатие + сдвиг» и представляют собой две перфорированные пластины с несколькими парами отверстий для крепления захватов, кососимметрично расположенных относительно плоскости склейки. Благодаря этим отверстиям можно изменять направление прилагаемой нагрузки. Одной из основных проблем при применении этих образцов является сильная концентрация растягивающих напряжений на краях образца, что вынудило исследователей искать пути решения по снижению опасных напряжений, инициирующих преждевременное возникновение трещин. Наиболее эффективное решение было предложено в работе [20]. Оно заключалось в придании краям образца особой формы в виде острого клюва, что позволило практически обнулить напряжения на опасных крае- вых участках, но в то же время привело к существенному увеличению трудозатрат и стоимости изготовления образца.

На рис. 1, a , приведено изображение модифицированного образца Аркана, который был применен нами для проведения испытаний. Он представляет собой составную конструкцию, состоящую из двух металлических половинок (рис. 1, b ), склеенных между собой при помощи вставок, которые испытываются на адгезионную прочность. На рис. 1, с приведены размеры образцов, использованных в работе. Металлические половинки жестко фиксируются в зажимах испытательной машины при помощи пластин, имеющих отверстия (рис. 2). В зависимости от того, какие из 5 пар отверстий будут использованы при закреплении пластины, можно ориентировать направление действия растягивающего усилия от 0 до 90° с шагом 22,5°.

b

Рис. 1. Общий вид модифицированного образца Аркана ( 1 – вставка из клеевого соединения, 2 – металлические части образца) ( а ); исходные металлические части образца до склеивания ( b ); модифицированный образец Аркана с указанием размеров в мм ( с )

Fig. 1. General view of the modified Arkan sample ( 1 – insert from adhesive joint, 2 – metal parts of the sample) ( a ); original metal parts sample before joining ( b ); modified Arkan sample with dimensions in mm ( с )

Рис. 2. Модифицированные образцы Аркана со вставками из клеевых соединений для определения адгезионной прочности при растяжении со сдвигом ( 1 – образец, 2 – пластины с отверстиями, 3 – зажимы испытательной машины). Угол α между осью растяжения и плоскостью соединения: а – 0; b – 45^○; c – 90^○

Fig. 2 Modified Arkan samples with inserts from adhesive joints for determining the adhesive strength under tension with shear ( 1 – sample, 2 – plates with holes, 3 – clamps of the testing machine). Angle α between the axis of tension and the plane of the joint: a – 0^○; b – 45^○; c – 90^○

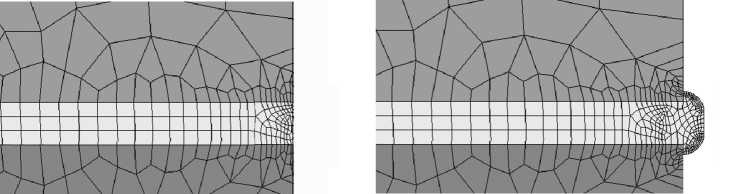
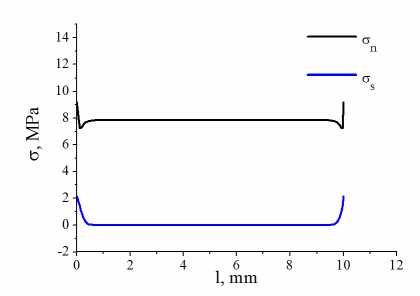
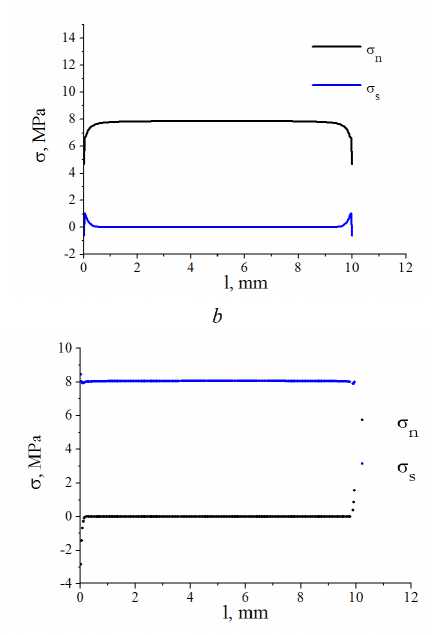
Напряженное состояние вблизи края образца может быть скорректировано путем изменения формы боковой поверхности адгезионного слоя. Для оценки возможности такой корректировки с использованием программного комплекса ANSYS было проведено конечно-элементное моделирование испытаний образцов на отрыв и сдвиг с плоской формой боковой поверхности адгезионного слоя (рис. 3, a) и с внешним клеевым буртиком (рис. 3, b). Одновременно рассматривали влияние фаски и скругления краев склеиваемых металлических образцов. Задачу решали в упругой постановке в условиях плоского напряженного состояния. При моделировании добивались максимальной равномерности распределения нормальных напряжений по границе соединения либо формирования локальных областей сжимающих напряжений вблизи кра- ев образца. Анализ полученных результатов показал, что наилучшим образом поставленной цели удовлетворяет формирование на краях образца небольшого клеевого грибовидного буртика толщиной, равной толщине клеевого слоя (см. рис. 3, b). Так, из представленных на рис. 4 данных следует, что на образце с буртиком при испытаниях на отрыв величина растягивающих напряжений снижается, а не увеличивается; при испытаниях на сдвиг нормальные растягивающие напряжения снижаются более чем в 7 раз, по сравнению с напряжениями на образце с плоской формой боковой поверхности. Это дает основание прогнозировать маловероятное возникновение краевых трещин расслоения. Что касается величины усилия растяжения, то она изменится незначительно в силу малой толщины клеевого буртика.

а                                      b

Рис. 3. Конечно-элементные модели склеенной вставки: а – с плоскими боковыми поверхностями адгезионного слоя; b – с грибовидным буртиком

Fig. 3. Finite element models of a glued insert: a – with flat side surfaces of the adhesive layer; b – with a mushroom-shaped flange

a

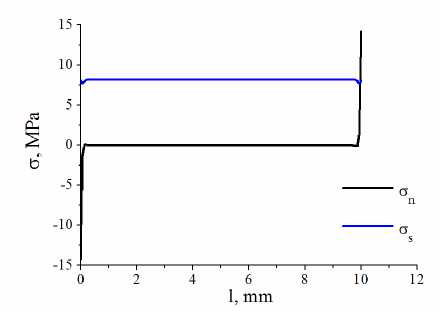
Рис. 4. Результаты моделирования напряженного состояния при плоской боковой поверхности клеевого слоя ( а, c ) и при наличии грибовидного буртика ( b, d ) в испытаниях на отрыв ( а, b ) и сдвиг ( c, d )

d

Fig. 4. Results of modeling the stress state with a flat side surface of the adhesive layer ( a, c ) and the presence of a mushroom-shaped flange ( b, d ) during tests for peeling ( a, b ) and shear ( c, d )

Металлические половинки образца изготавливали фрезерованием. Шероховатость на контактных поверхностях после механической и абразивной обработки контролировалась на бесконтактном профилометре-профилографе NT1100 и составила Ra 0,4 мкм. Склеивание осуществляли в специальных ограничивающих упорах, обеспечивающих постоянную толщину адгезионного слоя, равную 0,2 мм. Профиль буртика удобно было формировать путем удаления с помощью специального шаблона избытков клея, выдавленного из-под контактной поверхности склеиваемых металлических половинок.

Испытания проводили на универсальной испытательной машине Zwick/Roell Z2.5, снабженной климатической камерой КТХ-20 и позволяющей проводить испытания при температурах от –80 до + 180 °С. Максимальное возможное усилие соответствует 2,5 кН. Запись диаграмм нагружения до разрушения испытываемого соединения осуществляли с использованием датчиков усилия и перемещения, входящих в комплектацию испытательной машины. Погрешность тензометра и датчика силы по сертификатам калибровки не превышала соответственно 0,31 и 0,38 % от измеряемой величины.

Как следует из результатов моделирования, выбранная форма боковой поверхности клеевого слоя в значительной степени затрудняет образование и распространение концевых трещин на границе соединения. Фактически напряженное состояние является однородным на более чем 95 % протяженности границы соединения. Поэтому для его оценки в момент разрушения могут быть использованы средние значения нормальных σ n и сдвиговых σ s напряжений:

P P σ _n =   cos( α ), σ _s =   sin( α ),

SS

где P – предельное усилие растяжения, фиксируемое силоизмерительным датчиком испытательной машины в момент разрушения клеевого соединения; S – площадь поверхности склеивания.

Несмотря на то, что первоначально модифицированные образцы Аркана предназначались для реализации схем нагружения «растяжение + сдвиг» и «сжатие + сдвиг», тем не менее при реализации последней дополнительно возникают изгибающие моменты, обусловленные наличием шарнирных соединений при фиксировании образца. Эти моменты неопределенным образом искажают напряженное состояние в испытываемом адгезионном соединении, поэтому нами модифицированные образцы Аркана использовались только для реализации схемы нагружения «растяжение + сдвиг».

• 1.2.    BNS-образцы

  Испытания на поперечное сжатие сплошных дисков, предложенные Carneiro (1947) и Akazawa (1953),

широко используются для оценки предела прочности бетонов и керамик [21–23]. Они также адаптированы и применяются для изучения влияния направления нагрузки на распространение трещин от краев концентратора напряжений в виде радиальной щели в центре образцов [24]. Помимо относительно простой экспериментальной процедуры удобство использования данного метода испытаний заключается в том, что любая комбинация типов нагрузки (сжатие + сдвиг) может быть достигнута с помощью соответствующего выбора угла наклона относительно направления нагружения и длины щелевого концентратора [25–27]. В работах [28; 29] BNS -образцы были использованы для изучения влияния напряженного состояния на прочность границы соединения металлического композита, полученного сваркой взрывом, и металлополимерного соединения.

Использованные нами BNS -образцы представляли собой две половинки цилиндра диаметром 20 мм, соединенные с помощью адгезива (рис. 5, а ). Перед формированием адгезионного соединения контактные поверхности обрабатывались фрезерованием и абразивом для достижения шероховатости Ra 0,4 мкм. Склеивание осуществлялось в специальных ограничивающих упорах, обеспечивающих постоянную толщину адгезионного слоя 0,2 мм.

Рис. 5. BNS -образец перед испытаниями (для фиксации требуемого угла α наклона границы соединения образец поддерживается пластилиновыми упорами) ( a ) и испытательная машина Instron 8801 с навешенным оборудованием ( 1 – климатическая камера, 2 – оптическая система трехмерного анализа деформаций Strain-Master) ( b )

Fig. 5. BNS-specimen before testing (the specimen is supported by plasticine stops to fix the angle α) ( a ) and the Instron 8801 testing machine with attached equipment ( 1 – climatic chamber, 2 – optical system for three-dimensional deformation analysis Strain-Master) ( b )

Так как испытания по схеме «сжатие + сдвиг» требуют усилий больших, чем это допускается испытательной машиной Zwick/Roell Z2.5, то испытания BNS-образцов проводили на универсальной испытательной машине Instron 8801 с максимальным усилием нагруже- ния 100 кН в климатической камере, входящей в комплект поставки испытательной машины (рис. 5, b). Охлаждение в камере осуществляли пропусканием паров жидкого азота, а нагрев – с помощью электрических тепловыделяющих элементов. Регулирование температуры с точностью ± 2 °С производили автоматически с помощью штатного программного обеспечения машины на основании данных измерений хромель-алюмелевых термопар. Погрешность датчика измерения усилия испытательной машины составляет ± 0,005 % от максимального усилия (5 Н), или принимается равной ±0,5 % от показаний датчика (выбирается большее значение); ход исполнительного органа равен 100 мм; точность измерения перемещения равняется ± 0,5 % от хода исполнительного органа (0,5 мм) При проведении испытаний придерживались рекомендаций [30] по ограничению скорости нагружения BNS-образцов величиной 0,0075 м/с. Нагружение проводили до момента разрушения адгезионного соединения, при этом видеосъемку и измерение перемещений осуществляли с помощью оптической системы трехмерного анализа деформаций Strain-Master. Усилие деформирования при испытаниях регистрировали с использованием штатных тензодатчиков испытательной машины. При установке образцов между плоскими бойками испытательной машины угол α между направлением сжатия и плоскостью клеевого соединения варьировали в диапазоне от 0 до 20°. Эксперименты проводили при температуре –50 ○С, поскольку в таких условиях клеевая полимерная прослойка ведет себя как упругий материал. Это дает возможность осуществлять конечно-элементное моделирование поведения материала при нагружении без учета вязкой составляющей. Определение вязкостных свойств рассматриваемых в работе материалов, это отдельная большая задача, и в рамках данной статьи не рассматривается.

При использовании BNS -образцов также необходимо было уделить внимание наличию концентраторов напряжения на границе между покрытием и металлической основой в краевой области образцов по аналогии с модифицированными образцами Аркана. Для этого в программном комплексе ANSYS было проведено конечно-элементное моделирование испытаний образцов с плоскими поверхностями адгезионного слоя (рис. 6, а ) и с небольшим вытеканием клеевой прослойки за пределы образца (рис. 6, b ). По результатам моделирования установлено, что форма боковой поверхности адгезионного слоя BNS -образцов не оказывает существенного влияния на величину и распределение напряжений в краевой области. Кроме того, в данной области в основном преобладают сжимающие напряжения, которые не будут инициировать разрушение.

Полученные данные по значениям нормальных и касательных напряжений в зависимости от угла наклона α позволяют сделать вывод, что BNS -образцов, также как и для модифицированных образцов Аркана, напряженное состояние остаётся однородным на более чем

95 % протяженности границы соединения. Поэтому для его оценки в момент разрушения могут быть использованы средние значения нормальных σ n и сдвиговых σ s напряжений, рассчитываемые по формуле (1).

Рис. 6. Конечно-элементные модели вставки: а – с плоскими боковыми поверхностями адгезионного слоя; b – с буртиком за счет вытекания клеевой прослойки за пределы образца

b

Fig. 6. Finite element models of a glued insert: a – with flat side surfaces of the adhesive layer; b – with a flange due to the adhesive layer flowing beyond the sample

• 1.3.    Трехточечный изгиб многослойных образцов

  Для оценки адгезионной прочности слоистых материалов наиболее часто используются испытания на сдвиг растяжением внахлестку (ГОСТ 14759-69, ISO 4587-79, ASTM Standard D1002-10), на четырехточечный изгиб образца с надрезанным наружным слоем [1], на изгиб со сдвигом (ГОСТ Р 57732-2017), на трехточечный изгиб (ГОСТ 25.604-82, ГОСТ Р 568102015, ASTM Standard D790-e2). При трехточечном изгибе реализуется неоднородное напряженное состояние, из-за чего ряд авторов не рекомендует использовать данную схему нагружения для оценки интегральных прочностных свойств материалов [31; 32]. Однако, с другой стороны, наблюдая за процессом разрушения в точках образца с разным напряженным состоянием, можно сократить количество проводимых экспериментов и получить больше экспериментальных данных, используя современные методы визуализации процесса испытаний и анализа экспериментальных данных.

Для трехточечного изгиба используются слоистые образцы, состоящие из пластин металла, соединенных прослойками адгезива (рис. 7). Чтобы сформировать одинаковую толщину адгезивных слоев, по краям пластин устанавливаются межслойные ограничительные прокладки. Количество слоев может быть различным, но чем толще собранный образец, тем больше реализуемый диапазон изменения характеристик напряженно-деформированного состояния.

Испытуемый образец устанавливается на боковые опоры (рис. 8, а) в рабочем пространстве испытательной машины. Нагружение осуществляется перемещением нижней траверсы машины с расположенными на ней боковыми опорами. Верхний захват с центральной опо- рой остается неподвижным. Прогиб образца в процессе испытаний измеряется с помощью специального датчика, расположенного под образцом (рис. 8. а).

Рис. 7. Многослойный образец для испытаний на трехточечный изгиб с нанесенными реперными линиями для фиксации межслоевого сдвига

Fig. 7. Multilayer specimen for three-point bending tests with reference lines applied to record interlayer shear

а

b

Рис. 8. Изгиб образца в процессе испытания ( а ), межслоевой сдвиг среднего слоя адгезива ( b )

Fig. 8. Bending of the testing sample ( a ), interlayer shear at the middle layer of adhesion ( b )

На боковую поверхность образцов наносятся реперные линии (фломастером или типографской краской), которые позволяют зафиксировать момент сдвига слоев адгезива относительно металлических пластин в процессе испытаний. Для этого проводится видеосъемка деформирования образца с помощью оптической системы трехмерного анализа деформаций Strain-Master. Момент локального адгезионного разрушения по механизму сдвига связывается с началом визуально различимого относительного смещения реперных линий на границах слоев, который определяется по результатам анализа последовательности кадров видеосъемки после проведения испытаний. На рис. 8, b , в качестве примера представлен один из кадров видеосъёмки, на котором показано смещение реперных линий на границе среднего слоя адгезива и металлической пластины.

Для определения значений характеристик напряженно-деформированного состояния в местах наблюдаемого адгезионного разрушения и их изменения в процессе трехточечного изгиба было осуществлено моделирование испытаний с использованием программного комплекса ANSYS. В силу симметрии процесса деформации моделировали 1/2 схемы испытания (рис. 9). Модель соединения представляла собой металлические пластины 1 , склеенные между собой адгезивными прослойками 2 . В первом приближении полагали, что возникновение сдвига по механизму адгезионного разрушения в каждом слое образца происходит независимого от других слоев. Такое допущение позволило использовать опцию bonded для соединения слоев модели без возможности относительного смещения в контактных плоскостях. Для конечно-элементной дискретизации модели использовали 8-узловые конечные элементы типа SOLID 185. Для осуществления контакта опор 3 , 4 и образца задавали контактные пары типа Surface-to-Surface со стандартным скольжением в контактной плоскости.

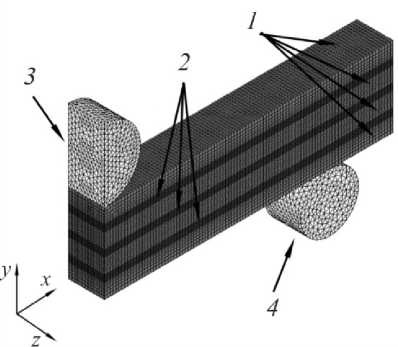
Рис. 9. Конечно-элементная модель при испытании на трехточечный изгиб: 1 – металлическая пластина;

2 – адгезив; 3 – центральная опора; 4 – боковая опора

Fig. 9. Finite element model for three-point bending test: 1 – metal plate; 2 – adhesive; 3 – central support; 4 – lateral support

Результаты моделирования позволяют получить значения компонент тензоров напряжений и деформаций во всех узлах конечно-элементной сетки на каждом расчетном шаге нагружения. Это дает возможность восстановить историю изменения напряженно-деформированного состояния от начала испытания до моментов наблюдения начальных относительных сдвигов реперных линий, классифицированных как локальное адгезионное разрушение по механизму сдвига. Сопоставляя результаты видеосъемки и моделирования, можно установить группу узлов конечно-элементной сетки, координаты которых в актуальной конфигурации соответствуют местоположению начальных относительных сдвигов реперных полос, а также номера расчетных шагов, ближайших к моменту видеофиксации сдвигов. Значения характеристик напряженно-деформированного состояния в этих узлах используются при составлении критерия, определяющего условие локального разрушения адгезионного соединения.

В целом неоднородность напряженно-деформированного состояния, провоцируемая трехточечным изгибом, позволяет по результатам моделирования одного испытания получить диапазон характеристик локальных напряжений и деформаций на каждом расчетном шаге нагружения в разных точках на всех границах слоев соединения. Это означает, что фактически при одном испытании мы имеем разные условия, которые могут провоцировать адгезионное разрушение исследуемого многослойного материала по механизму сдвига. Ниже, в качестве примера, будут приведены распределения нормальных и касательных напряжений на одной из межслойных границ. Величина этих напряжений и их соотношение показывают наиболее опасные участки с точки зрения сохранения локальной адгезионной прочности.

2.    Обработка результатов экспериментов и обсуждение 2.1.    Критерий разрушения адгезионного соединения

В качестве критерия, определяющего условие локального разрушения адгезионного соединения, будем использовать достижение величины плотности энергии деформации предельного значения W * в некотором условном выделенном микрообъеме, включающем границу соединения. Условный выделенный микрообъем, изображенный на рис. 10, состоит из двух частей. Часть толщиной h 1 принадлежит адгезиву, а часть толщиной h 2 – субстрату. Микрообъем в данный момент времени находится в равновесии, и на его противоположных гранях действуют равные напряжения σ ij в локальной системе координат ( x′, y′, z′ ). Ось z′ направлена по нормали к границе соединения, а оси x′ , y′ лежат в ее плоскости.

Адгезив

Субстрат

Рис. 10. Условный выделенный микрообъем на границе соединения

г

Й1

\

Fig. 10. Selected microvolume at the boundary

Напряжения σ ij и соответствующие им деформации ε ij определяются из решения задачи механики по нахождению напряженно-деформированного состояния соединенных твердых тел под действием внешней нагрузки. В нашем случае будем считать, что условный выделенный микрообъем находится в условиях плоского напряженного состояния под действием нормального и сдвигового напряжений, определяемых по формулам (1). При проведении испытаний ниже температуры стеклования, можно считать, что разрушение адгезионного слоя происходит в области упругих деформаций.

Предельную плотность энергии деформации условного выделенного микрообъема W * и ее компонент при разрушении соединения определяли по формулам

W * = W * + W * , W * = -L ( ст 2 -vc 2, с 2 +СТ 2, ), 2 E

W s^*

е^—

— , G — , 2 G 2(1 + v )

где W n * , W s * – нормальная и сдвиговая компоненты плотности энергии деформации; E , G , ν – эффективные значения нормального модуля упругости, модуля сдвига и коэффициента Пуассона.

Эффективные значения характеристик упругих свойств могут быть рассчитаны с использованием известных формул для однонаправленных композитов:

h _ hl h2 ,. _ V1 hlE2 +V2h2E1 h _ h h2 E~E1 E2, " hE2 + h2E1 , G~G1 G2, где E1, ν1, G1 и E2, ν2, G2 – значения нормального модуля упругости, коэффициента Пуассона и модуля сдвига материалов адгезива и субстрата, соответственно.

Непосредственно формулы (3) применить для расчетов не представляется возможным, так как значения толщин слоев h 1 и h 2 условного выделенного микрообъема являются введенной физически неопределенной математической абстракцией. Физический смысл может иметь их соотношение, которое характеризует вовлеченность обоих материалов в процесс адгезионного взаимодействия. Предположим, в первом приближении, что данное соотношение обратно пропорционально значениям нормальных модулей упругости адгезива и субстрата, т.е.:

h = h 2 E ² , E ₁

Тогда после несложных преобразований (4) получим формулы для расчета эффективных значений E , G и ν для условного выделенного микрообъема, не содержащие h 1 и h 2 :

^E ₁ + E 2       V _t ^E 2 ^+v 2 E ₁        G 1 ⁺ G 2

E- ₊ E^ ,       E 2 + E 22 ’ G ₊ G .

E 2 E 1                         G 2 G 1

Для количественной оценки влияния напряженного состояния на прочность адгезионного соединения целесообразно использовать зависимость W* от фазового угла β, который рассчитывается по следующей формуле:

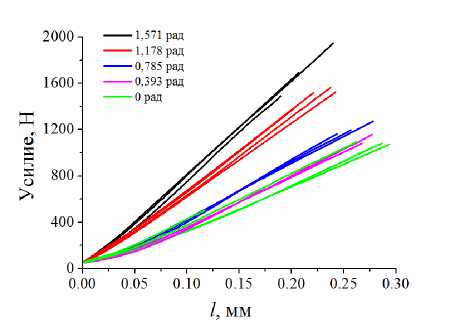
Рис. 11. Диаграмма нагружения для образцов Аркана при разных углах α

Fig. 11. Load diagram for Arcana samples at different angles α

₽ = arctg I I, 1° s J

так как при этом график W *(β) не будет иметь разрыва в отличие от функции W *(α).

Зависимость W *(β) отражает влияние нормальных напряжений на разрушение адгезионных соединений по механизму расслоения: при β > 0 на границу соединения действуют внешние растягивающие нормальные напряжения, провоцирующие расслоение; при β < 0 – действуют сжимающие нормальные напряжения, которые затрудняют расслоение; β = 0 соответствуют напряженному состоянию простого сдвига, когда действие нормальных напряжений отсутствует.

2.2. Примеры использования методик

Экспериментальные и расчетные данные для построения диаграмм предельной плотности энергии деформации адгезионного соединения АМг5/ЭД-20/АМг5

Experimental and calculated data for diagrams of the ultimate deformation energy density of the adhesive joint AMg5/ED-20/AMg5

Адгезионное соединение АМг5/ЭД-20/АМг5.

В данном соединении роль субстрата выполняли образцы из алюминий-магниевого сплава АМг5, а в качестве адгезива использовалась эпоксидная смола ЭД-20. Для проведения испытаний были изготовлены вставки к модифицированным образцам Аркана и BNS -образцы по методике, описанной выше. При формировании адгезионного соединения эпоксидная смола отверждалась с использованием диэтилентриамина (ДЭТА) в соотношении 10:1 при комнатной температуре. Испытания проводили при температуре –50 ^○С со скоростью нагружения 1 мм/мин. Диаграммы нагружения для образцов Аркана при разных углах α показаны на рис. 11. Площадь адгезионного контакта S у образцов Аркана составляла 150 мм², у BNS -образцов – 400 мм². Усредненные по результатам испытаний 3–5 образцов экспериментальные данные приведены в таблице.

Необходимые для расчета контактных напряжений значения модулей нормальной упругости для материала субстрата и адгезива определяли на приборе динамического механического анализа GABO NETZSCH DMA EPLEXOR 100N при температуре –50 ○С в испытаниях на сжатие цилиндрических образцов с частотой 1 Гц.

α, градус	Р , кН	β, рад.	σ n , МПа	σ s , МПа	W n * , Дж/м2	W s * , Дж/м2	W* , Дж/м2
90	1,68	1,571	11,2	0	12,44	0	12,44
67,5	1,51	1,178	9,32	3,86	8,66	4,02	12,68
45	1,06	0,785	4,98	4,98	2,47	6,70	9,17
22,5	1,11	0,393	2,83	6,84	0,80	12,62	13,42
0	1,26	0	0	8,37	0	18,93	18,93
-6,9	7500	-0,121	-18,62	2,25	34,53	1,36	35,89
-11,5	9820	-0,200	-24,06	4,88	57,70	6,42	64,12
-15	13500	-0,262	-32,51	8,71	105,32	20,48	125,80
-20,5	18900	-0,356	-51,60	19,19	265,34	99,41	364,75

Примечание: значения угла α для испытаний BNS-образ- цов взяты со знаком минус.

В этих условиях эпоксидный адгезив находится в остеклованном состоянии и слабо проявляет вязкостные свойства, поэтому определённое в экспериментах значение модуля накопления E ´ практически равно значению нормального модуля упругости Е 1 = E ´ = 4,72 ГПа. Значения коэффициента Пуассона ν 1 = 0,35 для эпоксидного адгезива и ν 2 = 0,33 для алюминиевого сплава были приняты из справочных данных [33; 34]. Путем подстановки указанных выше значений упругих констант в формулы (5) были рассчитаны эффективные значения характеристик упругих свойств: E = 5,02 ГПа, G =1,86 ГПа, ν = 0,35. По результатам экспериментов были определены значения компонент предельной плотности энергии деформации W n * и W s *, а также значения W* , которые приведены в таблица. Диаграмма предельной плотности энергии деформации W* (β) показана на рис. 12.

Следует отметить, что использование фазового угла β является более удобным для наглядной оценки

влияния напряженного состояния на предельную плотность энергии деформации адгезионного соединения, чем применяемый рядом авторов [35–37] фазовый угол ψ, рассчитываемый по формуле:

у = arctg

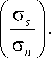
Это связано с тем, что график W *(ψ) имеет разрыв при ψ → 0 в области ψ < 0.

Графическая зависимость W* (β), как это видно из рис. 12, представляет собой гладкую функцию, которая может быть аналитически описана уравнением:

log W ’ ( P ) = C i exp( - c 2 P ) + c 3 ,             (8)

где с 1 , с 2 , с 3 – эмпирические коэффициенты, значения которых для данного адгезионного соединения равны 0,319, 4,194 и 1,045 соответственно.

Зависимость W *(β) можно использовать в качестве критерия локального разрушения по механизму расслоения в адгезионных соединениях конструкций и в ме-таллополимерных композитах. В этом случае степень использования ресурса прочности соединения Ψ и его остаточный ресурс Ψ res могут быть количественно оценены по следующим формулам:

WW -------. w _= 1--. W ’ ( p )      ст W ’ ( p )

где W – локальная плотность энергии деформации в наиболее напряженном (опасном) месте клеевого соединения в рассматриваемый момент времени.

Параметры Ψ и Ψ res удобно использовать при осуществлении проектных и поверочных расчетов адгезионных соединений.

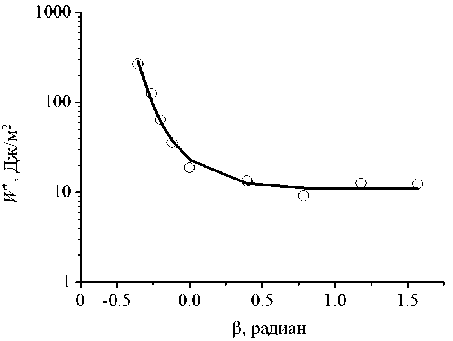
Рис.   12. Диаграмма предельной плотности энергии деформации адгезионного соединения АМг5/ЭД-20/АМг5. Точки на рисунке соответствуют данным, приведенным в таблице, линия – аппроксимирующей зависимости (8)

Fig. 12. Diagram of the ultimate density of deformation energy of the adhesive joint AMg5/ED-20/AMg5. The points in the figure correspond to the data given in Table, the line corresponds to the approximating dependence (8)

Адгезионное соединение АМг6-НВП/ЭД-20/АМг6-НВП. Слоистые образцы, состоящие из четырех пластин алюминиевого сплава АМг-6-НВП, соединенных прослойками адгезива, подвергали испытаниям на трехточечный изгиб (рис. 7, 8). Размеры пластин составляли 80×10×2 мм (длина × ширина × толщина). Сплав АМг6-НВП представляет собой сплав АМг6 с химическим составом по ГОСТ 4784-97, который для увеличения прочности подвергается холодной пластической деформации прокаткой. В качестве адгезива использована эпоксидная смола ЭД-20, отвержденная полиэтиленполиамином (ПЭПА). Массовое соотношение смола/отвердитель составляло 10:1. Отверждение смолы осуществляли при температуре 25 ° С. Толщина слоев адгезива в среднем составляла 1 мм. Испытания на трехточечный изгиб проводили при комнатной температуре на универсальной серво-гидравлической испытательной машине Instron-8801 со скоростью перемещения плунжера 1 мм/мин. Расстояние между осями боковых опор составляло 60 мм. Диаметр средней цилиндрической и боковых опор равнялся 10 и 8 мм соответственно.

В процессе испытаний по результатам видеосъемки были зафиксированы местоположения возникновения сдвигов реперных линий и соответствующие им величины прогибов. Сопоставление этой информации с результатами моделирования позволило провести анализ напряженно-деформированного состояния в местах разрушения адгезионного соединения и рассчитать для этих точек значения предельной энергии деформации. Необходимые для расчета эффективные значения упругих характеристик материалов адгезива и алюминиевого сплава были заимствованы из статьи [38]: E =4,77 ГПа, G =1,76 ГПа, ν =0,35.

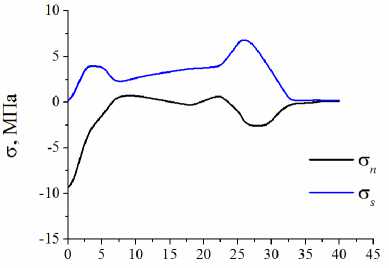
Установлено, что возникающие в результате изгиба нормальные σ n и касательные σ s напряжения на границах соединения слоев формируют сложное неоднородное напряженное состояние и определяют локальные условия нарушения или сохранения целостности адгезионного контакта. В качестве примера на рис. 13 приведено распределение σ n и σ s на границе между 2-м слоем адгезива и пластиной, где по результатам видеосъемки были зафиксированы первые сдвиги при величине прогиба образца 0,31 мм. Отрицательные значения σ n наблюдаются на участках локального сжатия в зонах влияния центральной и боковой опор при x < 6 мм, 22 <  x <33 мм. Эти участки следует рассматривать как области с неразрушенной адгезионной связью. На участке с положительными нормальными напряжениями разрушение адгезионного контакта наиболее вероятно.

Диаграмма предельной плотности энергии деформации, построенная по результатам обработки экспериментальных данных и численного моделирования, представлена на рис. 14. При наличии растягивающих напряжений нормальных к плоскости адгезионного соединения (р > 0) величина Wt * (р) мала, что свидетель- ствует о низкой адгезионной прочности сдвигу. В то же время в условиях действия сжимающих нормальных напряжений (β < 0) величина предельной плотности энергии деформации интенсивно возрастает.

X, мм

Рис. 13. Распределение нормальных σ n и касательных σ s напряжений на границе между 2-м слоем адгезива и пластиной, считая от нижней поверхности образца при величине прогиба образца 0,31 мм

Fig. 13. Distribution of normal σ n and tangential σ s stresses at the boundary between the second adhesive layer and the plate, measured from the lower surface of the sample with a sample deflection of 0.31 mm

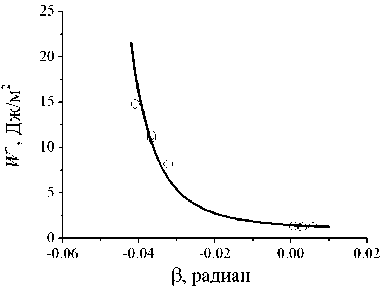
Рис. 14. Диаграмма предельной плотности энергии деформации адгезионного соединения «АМг6-НВП/ЭД-20/ АМг6-НВП»

Fig. 14. Diagram of the ultimate deformation energy density of the adhesive joint "AMg6-NVP/ED-20"

Точки на диаграмме соответствуют моментам локального адгезионного разрушения и связываются с началом визуально различимых межслойных сдвигов,