Комплекс программ для расчета распространения загрязнения методом клеточных автоматов

Данная работа посвящена комплексу программ, созданных на базе вероятностных клеточных автоматов (КА) [4]. Разработанные ранее авторами имитационные модели [4-6] модели имитируют атмосферные процессы (диффузию, седиментацию, ветровой массопе-ренос, вторичный массоперенос и др.). В рамках парадигмы КА данные математические модели описываются правилами КА [7]. Комплекс позволяет задавать форму источников загрязнения (точечный, линейный, площадной), их мощность, произвольные начальные и граничные условия (замкнутые, открытые) и др. параметры. В соответствии с парадигмой КА, моделирование производится на дискретной матрице пространства, временная ось разбита на равные промежутки времени – итерации [5, 6]. Результатом моделирования является матрица состояний клеточного автомата, ее аналогом можно считать сеточную функцию, получаемую при решении методом конечных разностей ДУ в частных производных [9]. Одной из отличительных особенностей метода клеточных автоматов является простота распараллеливания алгоритма за счет ограниченного числа участвующих в расчетах соседствующих клеток, называемых окрестностью. Функционал комплекса расширяется при добавлении новых правил КА за счет модульности, см. табл. 1, рис. 1. В блоке «настройка эксперимента» указываются начальные и граничные условия, набор используемых правил, настройка входных параметров каждого правила, количество экспериментов, количество итераций, размерность матрицы состояний и др. параметры. Особенностью имитационного моделирования и, в частности, метода вероятностных КА, является невозможность предсказать результат расчета без проведения компьютерного эксперимента. Точный результат моделирования изменяется от эксперимента к эксперименту, воспроизводятся его статистические характеристики.

Таблица 1. Структура программного комплекса имитационного моделирования

Модуль настройки компьютерного эксперимента
Пространства	Правила	Модули
поверхность атмосфера концентрация	эмиссия ветровой массоперенос седиментация диффузия вторичный массоперенос	модуль представления модуль расчета статистических данных
Справочник доступных окрестностей

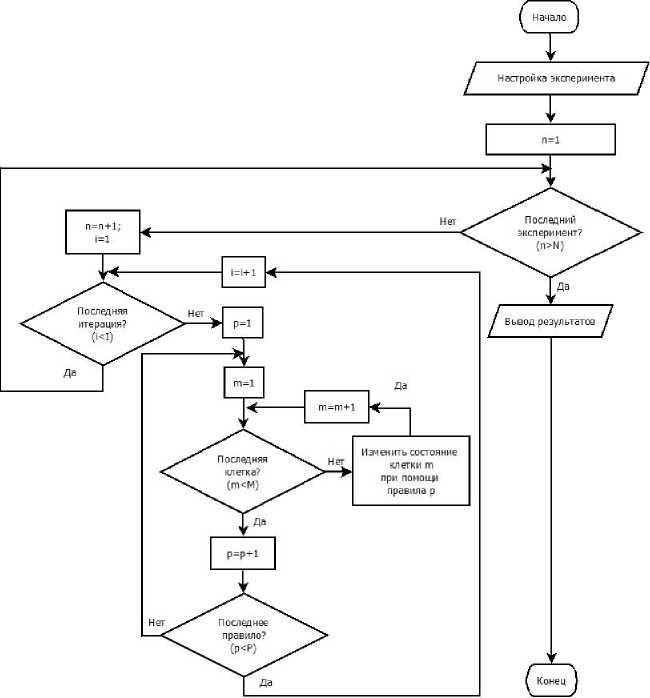
Рис. 1. Блок схема работы программного комплекса

Структура комплекса программ. Комплекс программ состоит из набора модулей (программ), по отдельности обеспечивающих расчеты массопереноса в результате моделирования следующих физических процессов: - эмиссия загрязняющих веществ;

• -    ветровой массоперенос загрязняющих веществ;

• -    седиментация (гравитационное осаждение, сухое осаждение);

• -    турбулентная диффузия;

• -    вторичный ветровой массоперенос;

• -    адсорбция молекул воды на поверхности аэрозольных частиц.

Математическое описание данных моделей и соответствующих им правила КА представлены в работах [4-6].

Проведем верификацию результатов имитационного расчета по отдельным программам (моделям) комплекса проведем путем сравнения с результатами расчета по аналитическим моделям, описывающим процессы мас-сопереноса. В качестве основной математической модели выступает уравнение турбулентной диффузии для приземного слоя воздуха. Для упрощения расчетов традиционно принимается независимость коэффициентов турбулентной диффузии от координат [8].

—+ и — д t д x

д s , д² s , д² s , д² s

Ю— = k x -у + k y -у + k z Т7 ⁺ f s ^{( x} , У , z , t ) д z д x ² д у ² д z ²

Модель распространения загрязнения под действием сухого осаждения и ветрового массопереноса. Аналитическая модель .

Уравнение (1) для одного процесса примет следующий вид:

• -    для седиментации

дs дs „ --ю— = 0 д t     дz(2)

для ветрового массопереноса дs

— + и— = 0 д t    дx(3)

Начальные условия двух моделей одинаковы:

s (x, у, z ,0) = f (x, у, z) = s 0 (x, у, z)

Решение уравнений (2) и (3) представляет собой функцию движения облака начального распределения вещества вдоль одной из заданной оси:

• -    для седиментации движение вдоль оси z по закону ^{z (} t ) = ^z 0 ^Ю t ■

• -    для ветрового массопереноса движение вдоль оси x по закону ^{x (} t ) = ^x 0 ^{+ ut}

Таблица 2. Параметры компьютерного эксперимента и аналитических моделей для процессов седиментации и ветрового массопереноса

Параметр	Аналитическая модель	Имитационная модель
начальные условия	[ 1, x = xn ] s 0( x ) = j         0 ^ 0, x ^ x0  x0 = 50 0J , 0        ,м	Cn , mr = xn { 5 ( mc ,0)} = j 0 , c 0 [ [ 0, m c * x 0 J
средняя скорость седиментации	® = 0.1, м/с	0.1, кл * /итер **
средняя скорость ветра	u = °- 5 , м/с	0.5, кл * /итер **
размерность матрицы	-	100x1x1, кл *
количество итераций	-	200, итер **
размер клетки	-	1, м
длительность итерации	-	1, с

Примечание: *кл - клетка (ячейка матрицы), ** итер - итерация

Имитационная модель. Соответствующие имитационные модели реализованы в отдельных программах комплекса. В основе работы одной модели лежит правило соответствующее сидиментации, в другой - правило ветрового массопереноса [4].

Модель распространения загрязнения под действием диффузии. Аналитическая модель. Рассмотрим одномерную диффузию без учета гравитационного осаждения и ветрового массопереноса, при действии мгновенного источника загрязнения, уравнение (1) имеет вид:

д s , д ² s

— = k_x —7

^д t       д x ²           (5)

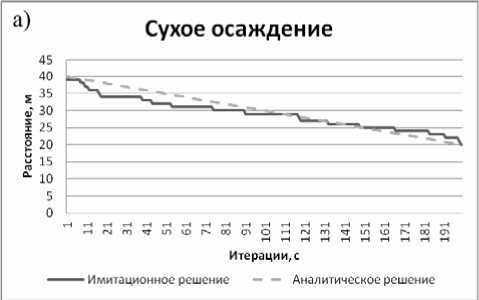
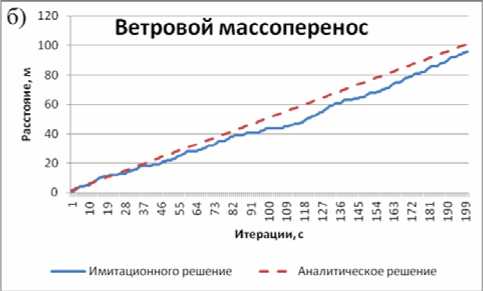
Рис. 2. Результаты расчетов по аналитическим и имитационным моделям:

а) распространение загрязнений под действием седиментации. б) распространение загрязнений под действием процесса ветрового массопереноса

Начальные условия s ⁽ x ,0) = 5 ( x ^- x о ) . Для постоянных коэффициентов турбулентной диффузии k i = const , решение уравнения (5) имеет вид:

- ⁽ x - x о )

S ( x . ' ) = „ , V„2 [ e  ^4V ]

^{(4 n} k x ' )                      (6)

Имитационное моделирование

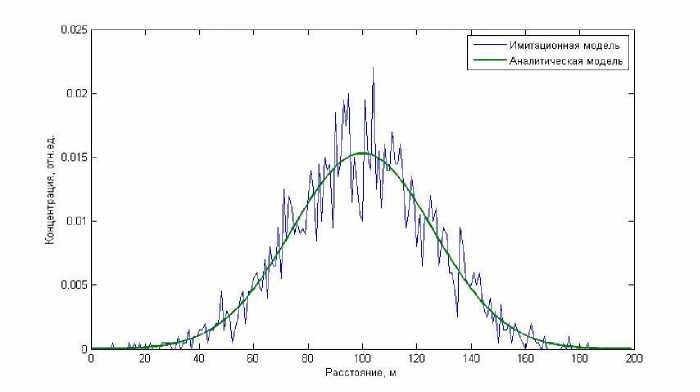
Таблица 3. Параметры имитационной и аналитической модели для турбулентной диффузии

Параметр	Аналитическая модель	Имитационная модель
начальные условия	f 1, x = x 0 1 s 0 ( x ) = L       r [ 0, x * x 0 , x. = 100 0        ,м	[ 1, m = xn ] { 5 ( mc ,0)} = Г c 0 k [ 0, mc * x 0 x 0 = 100 кл
коэффициент диффузии	kx = 3.5 2, x       ,м /с	-
размерность матрицы	-	200x1x1, кл
размер клетки	-	1, м
длительность итерации	-	0.1, с
количество экспериментов	-	2000
окрестность диффузии	-	N ( my ) = { mk i e M &| i - k | < 0}

Рис. 3. Результаты расчетов по аналитической и имитационной модели распространения загрязнения под действием диффузии (1000 итераций, усреднение по 2000 экспериментов)

Выводы: разработанный комплекс программ имитационных моделей позволяет рассчитывать поля поверхностных загрязнений, сформированных под действием различных процессов (ветровой массоперенос, седи ментация и диффузия). В работе показано, что расчеты, выполненные с помощью имитационных и аналитических моделей, согласуются. Особенностью результатов расчетов является гладкая (усредненная) зависимость концентрации загрязняющих веществ, как от времени, так и от расстояния до источника, что не подтверждается при проведении натурного эксперимента [10]. С другой стороны результаты, полученные с помощью имитационных моделей, имеют зашумленный вид вследствие стохастической природы правил массопереноса КА, что лучше соответствует реальным данным. Разработанный программный комплекс позволяет моделировать процессы ветрового массопере-носа веществ, процессы адсорбции молекул воды на поверхности аэрозольной частицы [5, 11], процессы вторичного ветрового массопе-реноса [6], процессы турбулентной диффузии и седиментации, учитывать суперпозицию источников загрязнений различной формы и также влияние сложных граничных условий.