Комплексирование сигналов в радиолокационных системах зондирования земной поверхности

щей поверхности, ее электрических параметров в определенном отражающем слое. Поэтому все РСА разделены на поддиапазоны.

Широкое применение в воздушно-космической разведке для пилотируемых летательных аппаратов нашел сантиметровый диапазон радиоволн λ = 1,67 – 3,75 см. Основными достоинствами данного диапазона радиоволн являются:

• 1)    сравнительно легкое дешифрирование РЛИ сантиметрового диапазона ввиду визуального сходства с привычными для восприятия человеком оптическими изображениями;

• 2)    объекты искусственного происхождения, имеющие, как правило, высокую эффективную поверхность рассеяния, легко дешифрирующиеся на РЛИ;

• 3)    широкое развитие технологий производства радиолокационных станций сантиметрового радиодиапазона и развитие алгоритмов обработки [1].

Однако, наряду с достоинствами «коротковолновых» диапазонов, имеется и ряд недостатков таких, как невозможность «подповерхностного» наблюдения скрытых объектов и большие потери при сложных метеорологических условиях.

Отмеченные недостатки устраняются путем увеличения длины волны зондирующего сигнала λ = 7,5 – 500 см. Использование длинноволновой части радиодиапазона позволяет обнаруживать объекты, скрытые под покровом леса, в земляных укрытиях, под снегом. Мешающие атмосферные факторы также снижают свое воздействие ввиду увеличившейся проникающей способности электромагнитной волны. В дециметровом диапазоне РЛИ может быть сформировано с разрешением до 1 м с достаточно высоким качеством, а на РЛИ метрового диапазона проявляются объекты, скрытые в лесу. Однако РЛИ становится мало узнаваемым из-за потери в яркости, а также из-за проявления на РЛИ изображений укрытых объектов [1].

Одной из перспективных тенденций развития РСА является использование многочастот-ности для обнаружения и опознавания скрытых объектов. При этом для многочастотного зондирования оптимальными следует считать диапазоны 2–5, 50–80 и 150–350 см [2]. Однако в современных комплексах дистанционного зондирования земной поверхности обработка РЛИ различных частотных диапазонов осуществляется раздельно и не учитывает корреляционные связи между РЛИ, формируемыми на разных частотах. В [3] обосновано наличие таких связей, разработаны модели пространственных корреляционных функций и определены их параметры для различных частотных диапазонов.

В связи с этим для повышения качества и информативности формируемых РЛИ предлагается проводить комплексную обработку сигналов РСА в различных диапазонах зондирующего сигнала с использованием байесовского подхода, учитывающего взаимосвязи между РЛИ на разных частотах.

Для решения задачи комплексной обработки РЛИ в различных частотных диапазонах в статье предлагается представить эти РЛИ в виде многокомпонентного случайного поля и воспользоваться методом оптимального восстановления случайных полей на основе байесовского подхода [4]. В общем виде постановка и решение задачи оптимального восстановления многокомпонентных статических случайных полей, согласно [4], выглядит следующим образом.

Исходя из физических соображений, плоское РЛИ можно представить в виде поля значений яркости, т.е. случайного поля, зависящего от пространственных координат u ( r ), где r – вектор пространственных координат [3].

Пусть на входе устройства обработки наблюдается l -компонентное случайное поле:

5(р ) = J F(р. r) u(r) dr+n(p) -

Здесь ξ( ρ ) – l -мерная случайная функция наблюдения переменной ρ ∈ P ; n ( ρ ) – l -мерный аддитивный гауссовский шумовой фон с нулевым математическим ожиданием и l × l корреляционной матрицей Q_n ( ρ ₁, ρ ₂); u ( r ) – информационный параметр, подлежащий восстановлению (оценке), который характеризует свойства формируемого РЛИ и является случайной m -компонентной функцией пространственных координат r ∈ Ω; F ( ρ , r ) – ядро интегрального преобразования (матрица размером l × m ), характеризующее свойства системы зондирования.

Априори предполагается, что оцениваемый параметр u ( r ) имеет гауссовское распределение с заданными параметрами: m -мерным вектором математических ожиданий m_u ( r ) и m × m априорной корреляционной матрицей R u ( r 1 , r 2 ).

Применительно к постановке задачи (1) оптимальный алгоритм для определения оцен-

-z             z ки m-компонентного поля u (r) = M {u (r) ^(р)} и m х m корреляционной матрицы ошибок

T I

R ( r , r ₂ ) = M | [ u ( r ) - u ( r ) ][ u ( r ₂ ) - u ( r ₂ ) ] | ^ ( p ) } будет иметь вид [4] ..

г^- ( г ) = JJ ^R ( r . ^r 2 ) R — ( r . ^r 2 ) m u ( r ) dr dr + °

⁺J JJ ^{R (} r , r D ^{F ( P} 2 , r D ^Qn ^{( P} 1 , ^P 2 Ж ^P 1 ) ^{d p} i ^{d p} 2^dr ‘ ,

П P

^R - ⁽ r i , ^r 2 ) = R u ^{- (} r i , ^r 2 ^{) +} JJ F ^{( р} 1 , ^Г 1 ) е ; ^{( p} i , ^p i ) F ^{( p} 2 , ^r 2 ) ^{d p} i ^{d p} 2 -

P

Конкретизируем общую постановку задачи (1) и её решение (2), (3) применительно к восстановлению РЛИ в двухдиапазонной РСА. В этом случае на входе двухканального приёмного устройства РСА наблюдаются сигналы в разных частотных диапазонах:

^ 1 ( t ) = J F ( t , r ) u 1 ( r ) dr + n 1 ( t ) ,

П                                                                   (4)

{ 2⁽ . ) = J F ² ( t . r ) u ² ( r ) ^dr + n ² ( . ) . r _en . . e^[ 0, T ^{] -}

Здесь роль переменной наблюдения ρ играет текущее время t из интервала наблюдения [0, T_н ]; F ( t , r ) – значения зондирующего сигнала F_i ( t ) i -го диапазона ( i = 1,2) в каждой точке r зондируемой плоской поверхности Ω = X × Y; r = [ x , y ], x ∈ X, y ∈ Y – вектор пространственных координат на плоскости Ω; u_i ( r ) – удельный коэффициент рассеяния зондируемой поверхности в i -м частотном диапазоне, характеризующий свойства формируемого РЛИ; n i ( t ) – независимые шумы в каналах приема, которые полагаются белыми гауссовскими с нулевыми математическими ожиданиями и спектральными плотностями N i .

В векторно-матричной форме уравнение наблюдения (4) может быть записано в таком виде:

^ ( t ) = J F ( t , r ) u ( r ) dr + n ( t ),                  r eQ , t e [ 0, T h ] .                  (5)

n

Здесь £ ( t ) = [ £ ( t\ £ ₂( t ) ] T ;

u ^{( r} ) = [ u i ^{( r} X u 2 ^{( r} ) ] T ;

R ( ,1,2 ) = M { [ u ( r ) - m u ( r ) ][ u ( - 2 ) - m „ ( г . ) ] ^ }4 R "< ^ '^ ^⁽ - )

¹                                           '    L ^R u 21 ⁽ r i ' r 2 ) ^R u 22 ⁽ r i ' r 2 )

F ( t ' r ) =

F ⁽ t ' ^r ) ⁰

^F 2 ⁽ t ' ^Г )

n = [ n ( t ) ' n 2 ( t ) ] T ;        (6)

Q n ( t i ' 1 2 ) = N 5 ( 1 2 - t i ) =    *

5 ( 1 2 - t i ) -

Следует отметить, что для обеспечения заданной разрешающей способности вдоль линии синтезирования апертуры антенны время наблюдения T i не должно быть меньше времени синтезирования.

Конкретизируя общий алгоритм восстановления статических случайных полей (2, 3) применительно к задаче комплексной обработки РЛИ в двухдиапазонной РСА (5, 6), получим:

^u i ( ^r ) = Jf L ^R ii ( ^r ' ^r ' ) ^F ( t ' ^r ' ) ^ ( t ) + ^R i2 ( ^r ' ^r ' ) ^F ( t ' ^r ' ) £ ( t ) ] ^dtdr' + ^Z i ( ^r ) '

T °                                                                      (7)

" / ( ^r ) = J J^[ R 22 ( ^r ' ^r ') ^F 2 ( t ' ^r ') ^ 2 ( t ) + R 2i ( ^r ' ^r ') ^F i ( t ' ^r ') ^ i ( t ) ] ^dtdr '+ ^Z 2 ( ^r ) '

T H n

T

н

1 -i

^{R ( r} i ' ^r 2 ) = ^R ;‘ ⁽ r , ^r 2 ^{) +}J F T ⁽ t i ' r ) N ^{- i F (} t 2 ' ^r 2 ) ^dt i ^dt 2     .

В алгоритме (7) аддитивные составляющие Z ₁( r ) и Z ₂( r ) характеризуют априорные сведения о формируемых РЛИ и в соответствии с (2) определяются выражениями:

Z1 (r) = JJ{[R11 (r,Г2)R- (r,Г2) + R12(r,Г2)R-1(r,Г2)]mM 1 (r)+

+ [R11 (r,r2)R„-- (r,r2) + R12 (r,r2)R^ (r,r2)]m„2 (r)}dridr2,

Z ^{2 (} r ) = JJ ^{{ [ R 21 (} r, r ² ) ^R u1 ^{1 ( r} 1 , r² ) ⁺ R ^{22 (} r, r² ) ^R u21 ^{( r} 1 , ^r 2 ) ] m u ^{1 ( r} ) ⁺

^                                                                   .(10)

+ ^{[ R} 21 ( ^r, ^r 2 ) R u ^ ( ^r 1 , ^r 2 ) + ^R 22 ( ^r, ^r 2 ) R ;\2 ( r ] , r 2 ) ] m u 2 ( r ] ) } drdr .

Структурная схема устройства комплексной обработки, реализующего оптимальный алгоритм (7), приведена на рис. 1.

Схема содержит два симметричных взаимосвязанных канала обработки. Копии зондирующих сигналов двухчастотных диапазонов, отраженных от разных точек земной поверхности, генерируются с помощью соответствующих опорных генераторов (ОГ) и фазовращателей (ФВ). Двойными линиями на схеме обозначены связи по всем значениям пространственных координат r . В блоке априорных данных (БАД) формируются априорные сведения в соответствии с выражениями (9), (10). В результате комплексной обработки на выходе устройства формируются в момент времени t = T i взаимозависимые оценки РЛИ U 1 ( r ) и й ₂ ( r ) .

Для определения качества работы синтезированного алгоритма было проведено его имитационное моделирование с учетом следующих допущений. При моделировании наблюдений ξ ₁( t ) и ξ ₂( t ) в качестве зондирующих сигналов использовались независимые шумоподобные гауссовские сигналы F 1 ( t , r ), F 2 ( t , r ). Особенности отражения этих сигналов в различных – 295 –

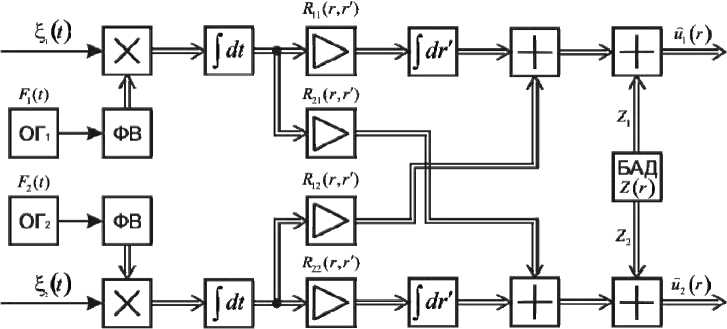
Рис. 1. Структурная схема двухканального устройства комплексной обработки

Fig. 1. Structural scheme of twin-channel device for combined treatment

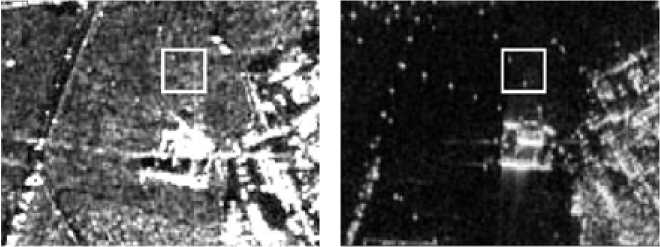
Рис. 2. РЛИ различных диапазонов длин волн: а – РЛИ X-диапазона ( λ X = 2,5 – 3,75 см); б – РЛИ L-диапазона ( λ L = 15 – 30 см)

Fig.2. Radar data of wave-length different range: а – Radar data of X range ( λ_X = 2,5 – 3,75 cm); б – Radar data of L range ( λ L = 15 – 30 cm)

частотных диапазонах учитывались с помощью удельных коэффициентов рассеяния u 1 ( r ) и u ₂( r ), в качестве которых использовались реальные РЛИ одного и того же участка местности в Х-диапазоне ( λ X = 2,5 – 3,75 см) и L-диапазоне ( λ L = 15 – 30 см). Данные РЛИ приведены на рис. 2.

На этих изображениях белым контуром отмечен характерный участок, на котором в L-диапазоне отчетливо видны изображения двух объектов, а в Х-диапазоне они практически незаметны. Это связано с особенностями отражающих слоёв разных диапазонов длин волн зондирующего сигнала [2]. Кроме того, РЛИ Х-диапазона характеризуется более «пёстрым» фоном по сравнению с РЛИ L-диапазона. Характерные участки РЛИ (в белом контуре на рис. 2) размером 20 на 20 пикселей, которые использовались при моделировании в качестве удельных коэффициентов рассеяния u 1 ( r ) и u 2 ( r ), представлены на рис. 3.

При использовании байесовского подхода к восстановлению случайных полей необходимым условием является наличие априорной информации. В данной задаче эта информация – 296 – заключена в пространственных корреляционных свойствах формируемых РЛИ. В [3] приведены выражения для априорных корреляционных функций РЛИ изображений, полученных на основе дифференцирования по пространственным координатам моделей полутоновых изображений в виде линейных стохастических дифференциальных уравнений в частных производных второго порядка. В данной работе рекомендовано для Х-диапазона использовать корреляционную функцию Ru11(r1, r2) смешанного типа с параметрами модели a1 = 3,27 и b1 = 3,1, а для L-диапазона – корреляционную функцию Ru22(r1, r2) комбинированного типа с параметрами модели a2 = 2,4 и b2 = 1,45. При этом взаимокорреляционная функция Ru12(r1, r2) определяется как

R u 12 ( r i ,^r 2 ) = 2

S 3 R H 12 ( У 1 , x i , у 2 , x 2 ) а ³ R H 12 ( У 1 , x i , у 2 , x 2 )

I                                                                                                  ,

• a y a х а x 2              a y a^ a y 2      J

где R H 12 – взаимокорреляционная функция исходных моделей полутоновых изображений для разных значений параметров a и b [5].

В результате статистического моделирования оптимального алгоритма (7)-(10) с учетом принятых допущений были получены комплексные оценки РЛИ выбранных характерных участков в разных диапазонах U 1 ( r ) и й₂ ( r ) . Результаты моделирования (при отношении сиг-нал/шум на входе приемного устройства, равном 5) представлены на рис. 4.

На рис. 5 изображены результаты моделирования алгоритма раздельной обработки сигналов двухдиапазонной РСА, который является частным случаем комплексного алгоритма (12) при условии R 21 = R 12 = 0.

Из анализа полученных результатов следует, что некоторые ярко выраженные объекты на РЛИ одного диапазона практически не просматриваются на РЛИ другого диапазона при раздельной обработке. В то же время при комплексной обработке специфические особенности формирования изображений в разных диапазонах в той или иной мере проявляются на обоих РЛИ.

Для оценки качества оценки формируемого РЛИ были расчитаны значения усредненной по пространственным координатам дисперсии ошибки

Рис. 3. Характерные участки РЛИ различных диапазонов длин волн: а – участок РЛИ X - диапазона; б – участок РЛИ L-диапазона

• Fig. 3.    Radar data patterns of wave-length different range а – Radar data of X-range; б – Radar data of L-range

  

  Рис. 4. Результаты комплексной обработки сигналов в двухдиапазонной РСА: а – комплексная оценка РЛИ X-диапазона; б – комплексная оценка РЛИ L-диапазона

  
  

• Fig. 4.    Combined treatment of signals results in two-range unattended ground sensor: а – combined evaluation of X range radar data; б – combined evaluation of L-range radar data

  
  
  

Рис. 5. Результаты раздельной обработки сигналов в двухдиапазонной РСА: а – раздельная оценка РЛИ X - диапазона; б – раздельная оценка РЛИ L-диапазона

Fig. 5. Particulate treatment results of signals results in two-range unattended ground sensor: а – particulate evaluation of X-range radar data; б – particulate evaluation of L-range radar data

R = ^ ^ r, r ) + . 2 ( r,r )] dr

– энергии зондирующих сиг-

E при отношении сигнал/шум qt = —-Ni

н

= 5, г = 1,2,гдеД=|F(t)dt налов. В выражении (11) дисперсии ошибок в разных частотных диапазонах R11(r, r) и R22(r, r) определяются в соответствии с выражением (8).

Расчеты показали, что усредненная по пространственным координатам дисперсия ошибки при комплексной обработке меньше усредненной по пространственным координатам дисперсии ошибки при раздельной обработке в 1,6 раза.

Для оценки информативности полученных изображений было рассчитано значение собственной энтропии восстановленных изображений [6], т. е.

i = 1,2,

E ( U ) = - Е P j ( u i ( ^r ) ) log 2 P j ( u i ( ^r ) ) , j = 0

где P j (U i ( r ) ) = N j / N - вероятность появления пикселя яркости j = 0,1,...,255 (гистограмма n(.

изображения); N j - количество пикселей изображения u i ( r ) яркости j ; N - число пикселей изображения u i ( r ) . Количественная оценка информативности комплексирования E o двух РЛИ оценивается как суммарный прирост разности энтропии между изображениями, полученными в ходе комплексной обработки, и изображениями, полученными при раздельной обработке, и определяется выражением:

E o = Е Е к ( U j — E E р ( i = 1,2, (13)

‘ n n n где Ек (Uj) - энтропия оценки комплексного изображения; Ер (ui) - энтропия оценки изображений при раздельной обработке.

Прирост разности энтропии при комплексной обработке составил 0,51, что свидетельствует о повышении информативности РЛИ, полученных в результате комплексной обработки.

Таким образом, из анализа полученных результатов можно сделать вывод о том, что комплексная обработка сигналов РСА в различных частотных диапазонах приводит к повышению информативности восстанавливаемых РЛИ и уменьшению дисперсии ошибки формируемых РЛИ по сравнению с раздельной обработкой.

Information capacity evaluation of Earth surface multispectral images. Vladimir-Suzdal. Materials of the 10-th International scientific conference “Physics and radioelectronics in medicine and ecology” (PhRЕME’2012), 2012, V.3. 161-165 p. (in Russian)]