Комплексная математическая модель оценки сейсмических рисков

Прогноз1 землетрясений является одной из злободневных проблем2 современности, имеющей не только3 научное, но и4 серьезное практическое значение [1–4]. Необходимость скорейшего решения проблемы прогноза землетрясений неуклонно возрастает, поскольку проводимые многими странами исследования говорят о том, что география сейсмической опасности не ограничивается общеизвестными высокосейсмичными зонами, но и охватывает многие регионы, ранее считавшиеся малосейсмичными и даже асейсмичными [5–8].

В XX веке предпринимались интенсивные международные попытки решить столь опасную для человечества проблему, однако они не увенчались каким-либо значимым успехом.

Так, по оценкам В.И. Кейлис-Борока, суще- ствующие системы прогноза землетрясений способны обеспечить следующие, сугубо вероятностные оценки точности его характеристик [9–10]:

• 1)    место готовящегося землетрясения – сотни километров;

• 2)    возможная энергия ожидаемого землетрясения – шесть порядков;

• 3)    время реализации – годы.

Совершенно очевидно, что такой прогноз никакой практической ценности не имеет. Помимо того что он может порождать ложную тревогу, он также способен породить и ложную успокоенность. Именно это произошло в 1989 г. в Калифорнии, когда сильное землетрясение ожидали в Паркфилде (300 км от Сан-Франциско), а оно произошло под Сан-Франциско.

В последние десятилетия в геофизике господствовали два кардинально противоположных подхода к оценке сейсмического риска.

Первый подход основан на прямом методе обнаружения местоположения очага готовящегося землетрясения – деформационно-геодезическом методе, который позволяет, как полагают его приверженцы, осуществлять точный прогноз места этого очага и определять максимально возможную силу будущего землетрясения.

ВЕСТНИК 2013 № 4

ВЕСТНИК 2013 № 4

Действительно, метод повторных геодезических измерений для изучения тектонических движений в связи с сейсмичностью, предложенный выдающимся русским ученым И.В. Мушкетовым еще в 1887 г., позволяет получать достоверные результаты по прогнозу землетрясения. Однако этот метод сопряжен со значительными материальными и финансовыми затратами, поскольку точность и достоверность прогноза напрямую связаны с плотностью прогнозных профилей, размещенных на исследуемой территории. В идеале все более или менее опасные в сейсмотектоническом отношении регионы должны быть опутаны сетью прогнозных профилей, что само по себе уже представляет трудновыполнимую задачу.

Второй подход основан на методе решения обратных задач – из анализа поведения аномалий в различных геофизических полях, так называемая стратегия аномалий. Подобная стратегия реализации прогноза землетрясений основана на идеях обнаружения очага и отслеживания происходящих в нем процессов по разрозненным косвенным признакам – аномалиям, порождаемым готовящимся очагом в различных полях: сейсмических, деформационных, гидрогеологических, геохимических, электромагнитных и других. Конечно, есть веские основания полагать, что в однородной изотропной среде местоположение готовящегося очага действительно можно было бы точно локализовать по подобным аномалиям, однако реальная среда неоднородна и не изотропна. Более того, она имеет мозаичное блоковое строение. Именно эти качества реальной среды и не позволяют приемлемо решить проблему прогноза землетрясений.

Ясно одно, проблемы защиты населения и территорий от воздействия опасных сейсмических процессов невозможно решать, не владея информацией об их пространственном распределении, интенсивности воздействия и периодичности проявления.

Для этой цели необходимо объединение обоих методов, из которых нужно взять самое ценное, достоверное, научно обоснованное и перевести это на язык математических моделей.

Комплексная математическая модель

Рассматриваемая в настоящей статье математическая модель оценки геодинамической устойчивости геосреды представляет собой синтез двух конкурирующих подходов к оценке сейсмического риска, господствующих в настоящее время в геофизике. То есть, объединяем в одной модели факторы влияния возмущений в геосреде, определяемых по косвенным признакам, в нашем случае – по аномальному гравитационному полю (вертикальная составляющая возмущений) [11–14] и современным движениям земной коры, основанным на данных повторных геодезических измерений, в частности по данным космической геодезии (горизонтальная составляющая).

Для иллюстрации сказанного отвлечемся на некоторое время от реальной геологической среды и представим себе однородное изотропное замкнутое упругое пространство в форме параллелепипеда – некоторую «плиту» с известными осредненными значениями плотности, модуля сдвига и модуля Юнга.

Также предположим, что эта среда («плита») рассматривается в рамках ньютоновской реологии, и на нее снизу вверх, строго в вертикальном направлении действует некоторая распределенная нагрузка P ( x , y ) (аномальное гравитационное поле), а в горизонтальном направлении, фиксируемая по данным измерений, действует нагрузка V ( x , y ) (смещения в геосреде), которые и образуют совместное внешнее воздействие на геосреду (рис. 1). В результате такого воздействия в изотропной среде («плите») возникают неоднородные по своей структуре поля напряжений и смещений.

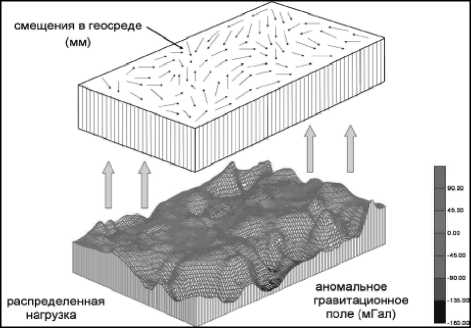
Рис. 1. Модель возникновения напряжений и смещений в упругом объеме геосреды при вертикально-горизонтальных возмущениях

В таком случае, например, распределенное внешнее воздействие P ( x , y ), известные дискретные значения которого заданы с некоторым фиксированным шагом по осям X и Y , представляются в виде ряда (1), т.е. выполняется разложение аномального гравитационного поля в изостатической редукции на составляющие его зональные гармоники:

P ( x , У ) = p ⁰ + ¹ ^P m 0 + ^{4     2} m = 1

lsl

+ ¹ Z P 0 n ' ZZ P mn , ² n = 1          m = 1 n = 1

где, например,

Подставив в систему (3) выражения для соответствующих компонент тензора напряжений, получим следующую систему уравнений для отыскания коэффициентов A , B , C , D :

k² ——— D - kA cos kx cos k y = P, cos kx cos k y , xykxy

I ^ + —     J

P mn = a mn cos ^k x x cos ^к у У ^{+ b} mn sin ^k x x cos M ⁺

⁺ c mn cos k x x sin ^к у У ⁺ d mn sin ^k x x sin ^к у У ";

4 ab amn =—J J P(x, У) cos kxx cos kyydxdy ; ab 00

- k x k y { [ k ( B + Dh ) + C ] shkh + [ k ( A + Ch ) + D J chkh } x x sin k x x sin k y y = — V_k sin k x x sin k y y ,

kk x | k ( A + Ch ) + X^х— D shkh + k ( B + Dh ) + X— C

X + —

chkh > x

,   nm  ,    nn kx=—; ky =-;:;

ab

a, b – соответственно, длина (X) и ширина (Y) рассматриваемой территории; p(x,y) – величины изостатических аномалий гравитационного поля.

Распределенная горизонтальная нагрузка V ( x , y ) в таком случае также должна быть представлена в виде подобного ряда (1).

Тогда компоненты тензора напряжений и составляющие вектора смещений в геосреде представляются аналогичным образом, например для нормальных компонент тензора напряжений соотношениями вида (2):

s

^P (x, y, z) = ^v + z^e+

^{4          2} m = 1

lsl

+ 1 Z - ⁿ ) - ZZ ^ -) ,                (2)

² n = 1             m = 1 n = 1

где в е { x , y , z , } .

Сформулируем граничные условия предложенной модели. Предположим, что к нижней поверхности упругого слоя приложена вертикальная распределенная нагрузка, а сдвиговые напряжения в вертикальных профилях на верхней и нижней поверхностях слоя равны нулю. Но поскольку у нас имеются на верхней поверхности слоя смещения, интерпретируемые как горизонтальная распределенная нагрузка на упругий слой, мы должны потребовать отличие от нуля сдвиговых напряжений в горизонтальной плоскости на верхней поверхности модели, и не просто их отличие от нуля, а соответствие им горизонтальной распределенной нагрузки.

В таком случае граничные условия для модели будут выглядеть следующим образом:

^ ( x , y ,0) = P ( x , y ), ^T xy ^{( x} , y , h ) = P V ^{( x} , y ), ^T xz ^{( x} , y , h ) = ⁰, ^T xz ^{( x} , y ^,0) = 0.

xsin k,x cos k,,y = 0, xy kk kB +--C sinkxcosky = 0. x       xy

I ^{X + —} J

Разрешая указанную систему уравнений относительно указанных коэффициентов, получим соотношения для компонент тензора напряжений и составляющих вектора смещений в геосреде, на основании которых и выполняется расчет ее геодинамической устойчивости. Последующий анализ состояния геосреды позволяет оценить сейсмический риск на какой-либо территории.

Результаты моделирования сейсмических рисков

Рассмотрим результаты математического моделирования, выполненные по вертикальногоризонтальной региональной модели оценки геодинамической устойчивости геосреды.

Эта модель была реализована для региона, включающего в себя часть территории Турции, Ирана, Ирака, Сирии, Азербайджана, Грузии, Армении, Украины, России (рис. 2).

ВЕСТНИК 2013 № 4

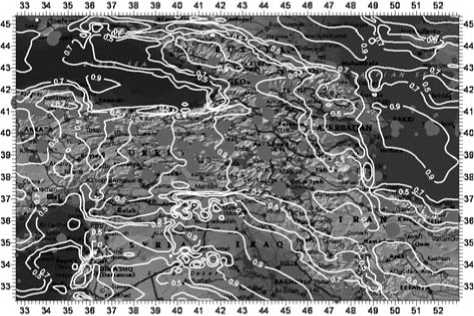
Рис. 2. Карта эквипотенциального распределения вероятностного показателя комплексного геодинамического риска с эпицентрами произошедших в данном регионе землетрясений с магнитудой от 5 до 7,8 с 1900 г. по 2010 г. [15], [16]

Применение модели к указанной территории во многом было связано с произошедшим 23 октября 2011 года землетрясением около города Ван в Турции. Для оценки сейсмических рисков был взят достаточно значительный по масштабу регион таким образом, чтобы озеро Ван оказалось в его центре (рис. 2). Авторы при этом располагали информацией о современных горизонтальных движениях земной коры по данным космической геодезии (рис. 3).

Представленная на рис. 2 карта наглядно свидетельствует об адекватности применяемой нами для оценок математической модели.

Мы провели дополнительную проверку модели на основании сопоставления ориентации векторов горизонтальных смещений на поверхности, полученных в результате математического моделирования (рис. 4) с информацией о современных движениях земной коры по данным космической геодезии (рис. 3). Сравнительный анализ представленных на этих рисунках карт показывает достаточно высокую точность используемой модели.

ВЕСТНИК 2013 № 4

Об учете релаксации напряжений и деформаций

Рассмотренная математическая модель описывает распределение смещений, напряжений и деформаций в геосреде, отвечающей законам ньютоновской реологии. Между тем, в реальности, особенно для прогностических оценок, необходимо учитывать влияние релаксации напряжений и деформаций на скорость их накопления в данной среде.

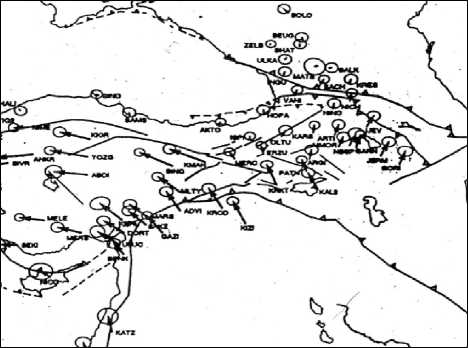
Рис. 3. Распределение векторов современных горизонтальных движений земной коры по данным космической геодезии

Как известно, в земной коре в условиях сжатия процесс разрушения происходит по схеме сдвига [17]. Оценка прочности среды в таком случае производится на основании следующего положения. Пластическая деформация, предваряющая разрушение, начинается при определенном значении объемной плотности потенциальной энергии формоизменения, так как при пластической деформации в среде невозможно ее накопление больше определенного предела прочности Aj. Пластическая деформация, предваряющая разрушение, не наступит до тех пор, пока плотность энергии формоизменения не превысит предела прочности для определенного типа пород земной коры.

Если скорость накопления упругой деформации очень мала, то напряжения будут релаксировать, и в этом случае энергия упругих деформаций будет диссипировать, переходя в тепло и энергию полиморфических и физикохимических процессов метаморфизма, и только малая ее часть будет накапливаться [18].

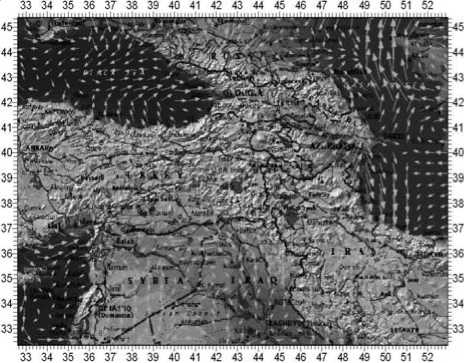
Рис. 4. Распределение векторов горизонтальных смещений на поверхности, полученных по результатам математического моделирования

Рассмотрим процесс нарастания деформации в среде, обладающей не только упругостью, но и вязкостью. Примем, что скорость деформации является величиной постоянной. Связь между сдвиговым напряжением и деформацией для упруго-вязкой среды (в плоскости XZ ) определяется уравнением:

1 d^z1 xz । д dt   n xz dt

• ¹    f ⁵ u x . ^d u z 1

где Yxz _ - I — + —— I - деформация; т — сдви-2 V dz говое напряжение; μ – модуль сдвига; η – дина мическая вязкость среды.

Обозначая для удобства —xz- = у'и drdt

• — = f_xz , перепишем (5) в виде:

dt x

τ′ τ xz +xz =γx′z .                                    (6)

µη

Выражение (6) представляет собой обыкновенное дифференциальное уравнение первого порядка (так как скорость деформации постоянна), и его решение записывается в виде:

τ xz ( t ) = ηγ x ′ z (1 - e ^{- t / δ} ),                           (7)

где δ=ηµ – время релаксации напряжений, определяемое через модуль сдвига и динамиче- скую вязкость среды.

Очень важным является вопрос об оценке величины скорости деформации γx′z . Получим формулу для оценки скорости деформации γx′z в вертикальной плоскости XZ. Вывод формулы основан на предположении, что деформации и, соответственно, сдвиговые напряжения являются функциями упругих и вязких свойств гео- среды.

Однако ввиду того что мы не знаем истинной величины «весового» вклада упругой и вязкой компонент геосреды, то, принимая для простоты расчетов, что «весовой» вклад упругих и вязких параметров геосреды одинаков, получим формулу для приближенной оценки скорости деформаций γx′z с учетом релаксации:

γ x ^′ z ⁼

τ (0) e - t / δ

µ t + η (1 - e ^{- t / δ} ) ,

где τ _x ⁽ _z ⁰⁾

начальное сдвиговое напряжение;

δ = ηµ – время релаксации; μ – модуль сдвига;

η – вязкость среды; t – время.

Таким образом, скорость деформации сдвига может быть оценена через начальное сдвиговое напряжение, параметры упруго-вязкой среды и время, прошедшее от начала накопления деформаций сдвига.

Заключение

Резюмируя все вышесказанное, отметим, что рассмотренная в настоящей статье комплексная математическая модель оценки геодинамиче-ской устойчивости гесреды, базирующаяся на совместном учете влияния возмущений в этой среде, определяемым как по аномальному гравитационному полю, так и по современным движениям земной коры, основанным на данных повторных геодезических измерений, позволяет более достоверно, по сравнению с так называемыми вертикальными моделями, выявлять на исследуемых территориях участки, наиболее опасные в сейсмическом отношении.

Еще больших результатов можно добиться при использовании подобных моделей, если в них будет рассматриваться максвелловская реология среды, позволяющая учесть влияние релаксации напряжений и деформаций на скорость их накопления в данной среде. Такой подход может позволить выполнить количественные оценки диссипации сейсмодеформационной энергии, что является очень значимым в плане осуществления прогнозных оценок сейсмичности.