Комплексная модель процесса разведки управляемых ракет с оптическими головками самонаведения

Современный этап развития средств вооруженной борьбы характеризуется широким использованием управляемых ракет (УР) с оптическими головками самонаведения (ОГС) для уничтожения летательных аппаратов (ЛА) противника. Это обуславливает необходимость создания бортовых комплексов обороны (БКО) ЛА, предназначенных для их защиты от УР. БКО включает в себя подсистему разведки (ПСР), подсистему создания помех (ПСП) и подсистему управления [1]. При проектировании и исследовании сложных технических систем, к которым обычно относятся системы вооружений, широко используют их моделирование [2]. В настоящей работе приводятся результаты разработки комплексной математической модели процесса разведки УР с ОГС с целью определения оптимальных структуры и значений параметров ПСР лазерного БКО ЛА.

Постановка задачи

Структурная схема модели ПСР представлена на рис. 1.

В общей структуре процесса разведки атакующих ЛА УР модель отражает подпроцессы поиска и обнаружения УР, определение типа ее головки самонаведения (оптическая/радиоло-кационная), измерение текущих координат, а также временной баланс работы ПСР. В отличие от известных моделей, формализующих вероятность успешного завершения поиска объекта, в нее дополнительно включены последовательно соединенные с модулем поиска модули, отражающие подпроцессы локационного наблюдения и обнаружения УР с ОГС. Модуль поиска позволяет проводить исследование эффективности поиска атакующей УР для двух вариантов построения ПСР (в обоих вариантах она состоит из пассивного и активного каналов). В первом варианте рассматривается ПСР на основе работающего в ИК- или УФ-области спектра пеленгатора и лазерного локатора. Пеленгатор осуществляет поиск и обнаружение атакующей УР по излучению факела ее двигателя, а с помощью лазерного локатора на основе бликовой локации производится определение типа ГСН УР, тем самым реализуется процедура двухэтапного просмотра заданной области пространства [3]. Во втором варианте построения ПСР рассматрива-

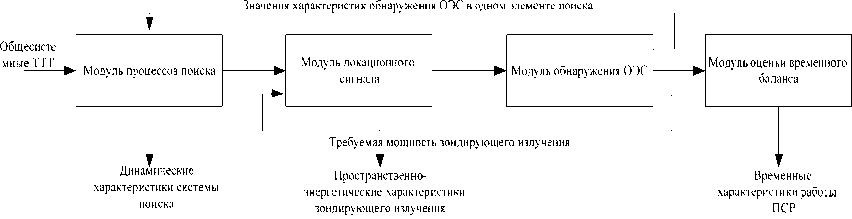
Рис. 1. Структурная схема комплексной модели процесса разведки УР с ОГС

Fig. 1. The Block diagramme of complex model of process of investigation Ur with OGS ется случай, когда в состав подсистемы включены УФ- и ИК-пеленгаторы, а также лазерный локатор [4]. Принятие решения об обнаружении атакующей УР может производиться с использованием логики как «И», так и «ИЛИ». Определение типа ГСН УР осуществляется по аналогии с первым вариантом построения ПСР.

Решение

В качестве показателей эффективности выполнения поиска формализованы финальная вероятность успешного завершения поиска P OD , вероятность успешного завершения поиска за заданное время P _D ( t ), а также среднее время поиска m_D. Данные показатели определяются следующими выражениями [3, 4]:

Первый вариант построения ПСР m n to to                              i—1

Pod = ZZZ Z P«P2k^D2k хП(1 - F j )ХП(1 - F2k )• a№; i=1 k=1 u=0 v=0                         j=1

m n to to                              i—1

PD (t) = ZZZZ P1iP2kD1iD2 k ХП(1 - F i] |M - F2 k )a Ubvh { t-( mu + ih -( nv + k )h 2 L i=1 k=1 u=0 v=0                         j=1

• m n to to                              i—1

mD = ZZZZ P1iP2kD1iD 2 k ХП(1 — F )П(1 — F2t )a W [(mu + i )h1 + ( nv + kh 2 ], i=1 k=1 u=0 v=0                         j=1

mm    nn где a0 =^Т1Д1 -£>1)П(1 -Fxj^; b =ZP2k (1-D2k)П(1-F2t); Pi, P2k- априорная вероятность на-'=1                       j=1                               k=1

t* k личия цели в i-том и к-том элементах разрешения секторов поиска первого и второго средства, осуществляющего поиск и обнаружение, соответственно; D1i, F1i, D2k, F2k – вероятности правильного обнаружения и ложной тревоги при обнаружении цели в i-том и k-том элементах разрешения секторов поиска; m, n – количество элементов разрешения в секторах поиска пассивного и активного каналов; h(∙) – единичная функция; τ1, τ2 – время просмотра одного элемента разрешения пассивным и активным каналом.

Второй вариант построения ПСР

• А. Решение об обнаружении цели принимается

• в соответствии с логикой «ИЛИ»

В данном случае вероятность P D ( t ) и финальная вероятность P OD определяются как вероятности выполнения хотя бы одного из двух событий: «произошло обнаружение цели в первом (втором) канале», т.е.

р -р +Р -Р .р

• ¹    OD    Odd 1 ^{+ 1} OD 2 ¹ OD 1 ¹ OD 2 ,

PD ( t )= PD1 ( t ) + PD 2 ( t ) PD1 ( t )' PD 2 ( t ), где POD1, POD2 – финальные вероятности обнаружения цели пассивным и активным каналами соответственно; PD1(t), PD2(t) – вероятности обнаружения цели к моменту времени t соответственно пассивным и активным каналами.

Математическое ожидание времени успешного завершения поиска определяется выражением

”

• m. = "F" J P (t) dt ■

OD 0

Вероятности P D 1 ( t ), P D 2 ( t ), P OD 1 , P OD 2 определяются выражениями, аналогичными

• --.*

PD1 ( t ) = EE EE P1iP2*D1iD2 * П(1 - FLO1 - F2t )a 0 ' b'lh { t - ( mu + i T - ( nv + k ) T 2 } , i=1*=1 u=0 v=0                      j=1'

m7-1

^p d 2 ( t ) = EEEE pa AAA K¹ - F o jlH ¹ - F 3 = ) a о • b iii h { t - ( mu ⁺ i ) ^T i - ( ' w ⁺ j ) ^т з } , ⁽⁴⁾

i=1 j=1 u=0 w =0                   O=1

POD1 = PD 1( t ) h (x )=1 ; POD 2 = PD 2( t ) h (x )=1, mm      n    n     '

где aEr,AD-H1-F1/); b1 =Ep*(1-DЙ1-F);b - =Ep3j(1-Dijjn1-F30); 1 — число элементов i=1                ,=1                       *=1                 '=1                      j=1

разрешения в зоне поиска лазерного локатора. Индексы 1, 2, 3 соответствуют характеристикам

ИК- и УФ-пеленгаторов, а также лазерного локатора. ^,

Выражение для математического ожидания времени успешного завершения поиска имеет следующий вид:

m = _L ( D 1 DL a (1 — b ) + DD b (1 — a ) ),                               (5)

P0 D < m • n            m • l ' у где a3 =]T]Tjrjr(1-ц)^-Fi)(m-1)u+i-1 <1-^(1-F2)(n-1)v+k-1((mu+i)t, -(nv+к)т2);

i = 1 k = 1 u = 0 v = 0

ml ro ro

Ь з = EEEE (1 - D 1 )^U(1 - F i )^{(m - 1)u + i - 1} • (l - D a ) w (1 - F 3 )^{(l - 1)w + j - 1}((mu + i) T i - (Iw + j) t ₃) ;

i=1 J=1 u=0w=0

_m__n_ to to a 4 =EEEE (1 - D1) u (1 - F1) ”" u+!" ^(1 - D 2)V(1 - F2) n” V+ ”;

i =1 k =1 u =0 x =0

b j m, E ^e^e (1 _D ) u (1 _Fi ) ( m -1) u +-1 (1 _D ) w (1 f ) ( l -1) w _{+ j - 1}

i =1 j =1 u =⁰ w =⁰

Б. Решение об обнаружении цели принимается в соответствии с логикой «И»

Когда решение об обнаружении цели принимается в соответствии с логикой «и», вероятности РOD, PD(t) определяются следующим образом:

P OD = P OD ¹ • P OD ² ;

Pd (t) = Pd 1(t) • Pd2(t), где PD1(t), POD2, PD1(t), POD2 определяются выражениями (4).

Математическое ожидание времени успешного завершения поиска может быть найдено по формуле mD =

f DD

1 a 3 b 4

P _{0 D} V m • n

D ₁ D ₃

+     b3 a m • l

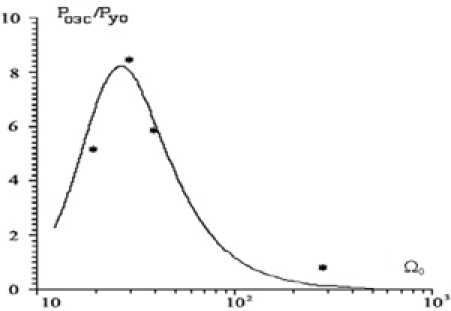
Рис. 2. Зависимость отношения P _оэс / P _уо от числа Френеля Ω₀

Fig. 2. Dependence of the relation P _оэс / P _уо on number of Frenelja Ω₀

Расчет характеристик обнаружения атакующей ракеты ИК- и УФ-пеленгаторами производится на основе модели излучения факела двигателя УР [5] с использованием методики [6]. Энергетическое ослабление излучения факела ракеты атмосферой может быть учтено известными методами [7]. Ниже остановимся на задаче обнаружения ОГС УР, решаемой в модулях локационного наблюдения и обнаружения ОГС разработанной модели.

В модуле локационного наблюдения ОГС производится описание процесса трансформации функции когерентности зондирующего излучения локатора при его распространении в турбулентной атмосфере от излучающей апертуры локатора к ОГС и обратно к фотоприемнику локатора. Упомянутая функция когерентности формализована для ОГС с матричным фотоприемником смотрящего типа [8]. На рис. 2 отражены результаты экспериментальной проверки данной модели. Сплошной кривой приведена зависимость от числа Френеля отношения средних мощностей локационного сигнала отраженного от ПНВ и уголкового отражателя, полученная с использованием разработанной модели. Знаком « ∗ » обозначены измеренные значения этого отношения. Данные результаты подтверждают возможность использования разработанной модели для описания локационного сигнала.

В модуле обнаружения ОГС формализован процесс принятия решения по достаточной статистике:

v 'v

L = JJ JJ x ^{( r}1 , t1 ) х ^{( r} 9^, t 9 ^{)V (} r ^, t l; ^r 9^, t 9) ^d rd rrdtidtr ,

±T sн формируемой на выходе приемника локатора по наблюдаемой аддитивной смеси реализации отраженного от ОГС поля и фона. Передаточная функция приемного устройства V(□) выявлена в результате решения интегрального уравнения Фредгольма второго рода, найденного с использованием разложения Карунена-Лоэва [9]:

P Ю

• V ⁽ x 1 , x 2 ) = TTT Z

N 0 n = ⁰

Ф n ⁽ x 1 ) Ф n ⁽ x 2 )

X n

p

• 1 + -c^—

N 0 X n

где x ₁ = t ₁ / T , x ₂ = t ₂ / T ; P_c , N ₀ – мощность локационного сигнала и спектральная плотность фона соответственно; φ n ( x ) – собственные функции; {χ n } – соответствующая система собственных значений интегрального уравнения

ф ( x ) = zf ^Rc ⁽ x , x iM x i ) dx                                                        ⁽⁸⁾

±1

и введения пробной системы ортонормированных функций, определенной на интервале [-1…1] и удовлетворяющей следующим условиям [10]:

J ± 1 V n ⁽ x i ) V k ^{( x} 2 ) Y c ⁽ x i , ^x 2 ) dx i dx 2 =5 n , k / X n J _v n ( x ) _V k ( x ) dx = 5 n k

± 1                               ,                      (9)

Jv n( x )V k ( x ) dx = 5 n, k ±i где γc(x1, x2) – положительно определенная функция, непрерывно симметрическая по обоим переменным; Rc(□) - временная корреляционная функция отраженного сигнала.

Для описания влияния динамических параметров локатора на эффективность разведки ОГС учтена связь между модулями поиска и обнаружения ОГС, которая порождена функциональной зависимостью показателей успешного завершения поиска от характеристик обнаружения ОГС. Для описания влияния характеристик приемопередающего устройства локатора на эффективность разведки учтена связь между подпроцессами обнаружения и локационного наблюдения ОГС, которая порождена функциональной зависимостью характеристик обнаружения от параметров оптических схем объектов разведки и параметров приемопередающего тракта локатора.

Заключение

Таким образом, разработанная модель подсистемы разведки позволяет комплексно исследовать показатели эффективности разведки УР с ОГС в зависимости от параметров их оптических схем и параметров ПСР, а также условий распространения излучения. Это открывает возможность оптимизации значений параметров подсистем разведки БКО ЛА.