Комплексная оценка упруго-пластических свойств материалов и систем для верха обуви

Приформовываемость верха обуви к стопе является одним из наиболее важных показателей качества обуви, определяющих её удобство в носке. Достаточную приформовываемость верха обуви к стопе в процессе эксплуатации можно обеспечить уже на стадии конструкторско-технологической подготовки производства путем рационального подбора комплектующих с необходимым комплексом упруго-пластических свойств. Однако, как было показано в работах [1– 5], упруго-пластические свойства материалов могут характеризоваться широким кругом показателей, определяемых по различным методикам и при различных видах деформации. В связи с этим возникла необходимость в снижении размерности исходного признакового пространства и выделении наиболее информативных признаков с точки зрения полноты и точности описания изучаемой характеристики.

Наиболее распространенным методом снижения размерности признакового пространства является метод главных компонент, представляющий собой метод преобразования исходной последовательности взаимосвязанных переменных x ij в новое множество независимых переменных F j , называемых главными компонентами, каждая из которых представляет собой ортогональную линейную комбинацию непосредственно измеренных на объектах исходных признаков:

F j = l 1j x 1 + l 2j x 2 + + l mj x m = L j ́ X;

m

J   £ 1 2 = i             (= 1, -, m

i = 1

m

У l-- ■ L = 0 (j,k = 1, -; m, i * k), ij ik i =1

где F j –j -тая главная компонента;

l j1 , l j2 , …,l jm – факторные нагрузки, характеризующие существенность влияния каждого фактора в вариации данного признака.

Учитывая то, что главные компоненты упорядочены по степени рассеяния в изучаемой совокупности объектов, т.е. первая главная компонента определяет максимальную дисперсию исходного массива признаков Х , а дисперсии последующих убывают с ростом номера компоненты, метод главных компонент позволяет осуществить переход к пространству меньшей размерности, используя минимальное число первых главных компонент, объясняющих наибольшую долю суммарной дисперсии исходных признаков.

Снижение размерности признакового пространства осуществлялось с использованием прикладного пакета программ «STATISTICA». Матрицы исходных данных Х «объекты – признаки» формировались по данным работ [1–5] и включали: для материалов наружных деталей верха 18 показателей упругопластических свойств, для текстильных материалов – 16 показателей, для систем материалов – 14 показателей.

По массивам исходных данных Х рассчитывались коэффициенты корреляции Пирсона между изучаемыми признаками и формировались корреляционные матрицы отдельно для материалов верха, текстильных материалов для межподкладки и подкладки и для систем материалов:

	(г r 11	r 12     .	r ..    r 1 m
R =	r 21 ...	r 22    . ...      .	..    r 2 m .. ...
	V r m 1	r m 2 .	У .. mm у

Для нахождения параметров модели (1) определялись собственные значения и соответствующие им собственные векторы построенных корреляционных матриц. Собственными значениями квадратной матрицы R порядка m называются такие значения λ j , при которых система следующих m уравнений имеет нетривиальное решение:

RL j = λ j L   ,                                           (3)

где L j –собственные векторы матрицы R , соответствующие λ j ;j=1,… m.

( R – λ j I) L j =0 ,                                       (4)

где I – единичная матрица.

Уравнение (4) имеет нетривиальные решения при условии, что определитель матрицы ( R – λ I ) обращается в нуль, т.е.:

rn - X R - XI\ = 0 или     A(X) = r21 r12      ...      r1m r22 — X -    r2 m = 0.     (5) rm1       rm2

г mm

- X

Так как порядок матрицы R равен m , то ∆(λ) является многочленом m -ой степени относительно λ, т.е.

∆(λ) = λ ^m + а 1 λ ^m-1+ …+ а m-1 λ + а m .               (6)

Корни уравнения ∆ (λ) = 0 дадут собственные значения λ 1 , λ 2 , … , λ m . Собственные векторы L j , соответствующие этим собственным значениям, образуют факторы F j . Элементы собственных векторов l j1 , l j2 , …,l jm представляют собой значения коэффициентов корреляции между соответствующими признаками и факторами. Чем теснее связь данного признака с рассматриваемым фактором, тем выше значение факторной нагрузки.

В соответствии с определением главные компоненты занумерованы в порядке убывания их дисперсий, т.е. S (F 1 ) > S (F 2 ) > … > S (F m ) , причем

S (F j ) = ∑( L j ́ X)² = L j ́RL j .                                  (7)

Умножив равенство (3) на L j ́ и сопоставив его с (7), получим, что

S (F j )= λ j .                                             (8)

Таким образом, величина λ j представляет собой не что иное, как часть суммарной дисперсии совокупности преобразованных данных, объясненную главной компонентой F j . Если переменные стандартизированы, то λ 1 > λ 2 > … > λ m , т. е. первые несколько членов разложения дают основной вклад в объяснение вариации величин исходных данных. В этом случае компоненты с малыми величинами собственных значений могут при анализе не учитываться и совокупность будет адекватно представлена с помощью первых k компонент.

Решение о том, сколько последних главных компонент можно без особого ущерба изъять из рассмотрения, сократив тем самым размерность исследуемого пространства, выносится на основании величины показателя полноты факторизации, характеризующего долю суммарной дисперсии, объясняемой первыми k компонентами:

Y = S^ • 100 = S(F) + S(F2) + - + S(Fk) • 100 Sm        S (F1) + S (F2) +... + S (Fm)

где S k = S (F 1 ) + S (F 2 ) + … + S (F k ) – полный вклад k компонент в суммарную дисперсию признаков;

S m – суммарная дисперсия всех признаков.

Таким образом, в результате реализации метода главных компонент получается информация об исследуемом явлении в сжатом виде.

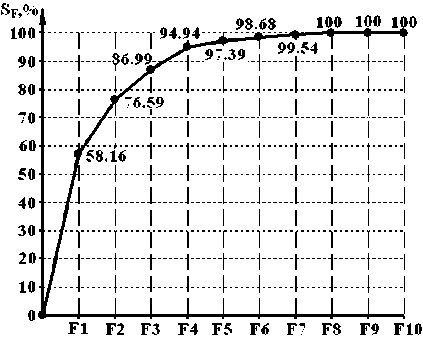
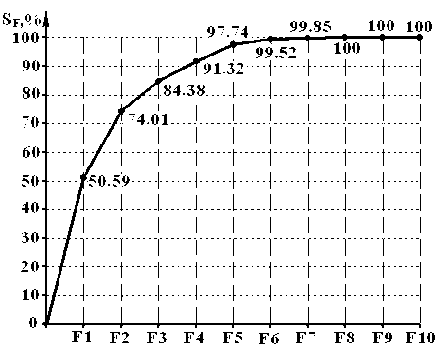
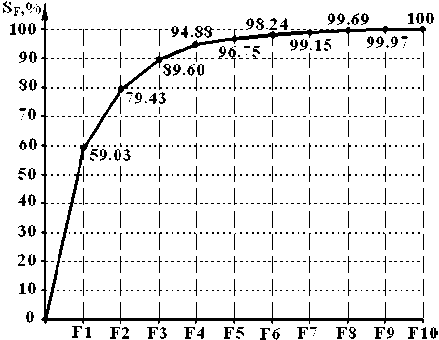
В ходе анализа внутренней структуры сформированных корреляционных матриц были получены собственные значения главных компонент, величины относительного и накопленного вклада главных компонент в дисперсии всех признаков. На рисунке 1 показано, что для наружных материалов верха и систем материалов в первых четырех главных компонентах аккумулируется около 95 % суммарной дисперсии исходных признаков. Для текстильных материалов 97,7% суммарной дисперсии приходится на первые пять главных компонент. Вклад последующих компонент в суммарную дисперсию признаков незначителен, а следовательно, их можно исключить из дальнейшего рассмотрения.

Анализ факторных нагрузок исходных признаков на выделенные главные компоненты показал, что для материалов наружных деталей верха обуви наиболее информативными показателями упруго-пластических свойств являются: пластичность на приборе ПОИК с относительной долей суммарной дисперсии 58,16 %; доля условно-эластической компоненты деформации при одноосном растяжении с относительной долей суммарной дисперсии 18,43 %; доля условнопластической компоненты деформации при одноосном растяжении с относительной долей суммарной дисперсии 10, 41 %; доля условно-эластической компоненты деформации при двухосном растяжении с относительной долей суммарной дисперсии 7,94 %.

Наиболее информативными показателями для оценки упруго-пластических свойств текстильных материалов можно считать: пластичность при одноосном растяжении до нагрузки 0,5 Р раз с относительной долей суммарной дисперсии 50,59 %; долю условно-эластической компоненты деформации при одноосном растяжении с относительной долей суммарной дисперсии 23,41 %; относительную затраченную энергию при одноосном растяжении до нагрузки 0,5 Р раз с долей суммарной дисперсии 10,37 %; долю условно-эластической компоненты деформации при двухосном растяжении с относительной долей суммарной дисперсии 6,94 % и пластичность при двухосном растяжении на приборе В 3030 с относительной долей суммарной дисперсии 6,42 %.

Для характеристики упруго-пластических свойств систем материалов наиболее информативными показателями являются: пластичность при двухосном растяжении на приборе В3030 с относительной долей суммарной дисперсии 59,03 %; относительная затраченная энергия при двухосном растяжении с относительной долей суммарной дисперсии 20,4 %; доля условно-упругой составляющей деформации при двухосном растяжении с относительной долей суммарной дисперсии 10,18 % и доля условно-эластической компоненты деформации при одноосном растяжении с относительной долей суммарной дисперсии 5,27 %.

Так как упруго-пластические свойства исследуемых материалов и систем характеризуются одновременно несколькими различными показателями, то для оценки их качества был использован комплексный метод, позволяющий получить итоговую оценку упруго-пластических свойств исследуемых объектов одним числом.

а)

б)

в)

Рисунок 1 – Накопленная дисперсия первых k главных компонент: а – для материалов наружных деталей верха обуви; б – текстильных материалов для подкладки и межподкладки обуви; в – для систем материалов

Для этого на основе выделенных наиболее информативных единичных показателей определялся комплексный безразмерный показатель упругопластических свойств материалов и систем по формуле

n

К_о = У К • m_t о    ii

,

i = 1

где К i – относительный единичный показатель упруго-пластических свойств;

m i – весомость i –го показателя свойств, определяемая по относительной величине вклада соответствующей главной компоненты в дисперсию всех признаков;

n – число учитываемых при комплексной оценке показателей.

Относительные единичные показатели определялись путем сравнения упругопластических свойств исследуемых материалов и систем с лучшим (максимальным или минимальным) значением показателя в данной группе объектов по формулам

К = — i max

X или     К, = —min-    , i Xi

где Х i – абсолютное значение единичного показателя упруго-пластических свойств.

Из приведенных формул выбиралась та, при которой увеличению K i соответствует улучшение приформовываемости верха обуви к стопе.

Значения комплексных показателей    упруго-пластических    свойств исследованных материалов и систем представлены на рисунках 2, 3.

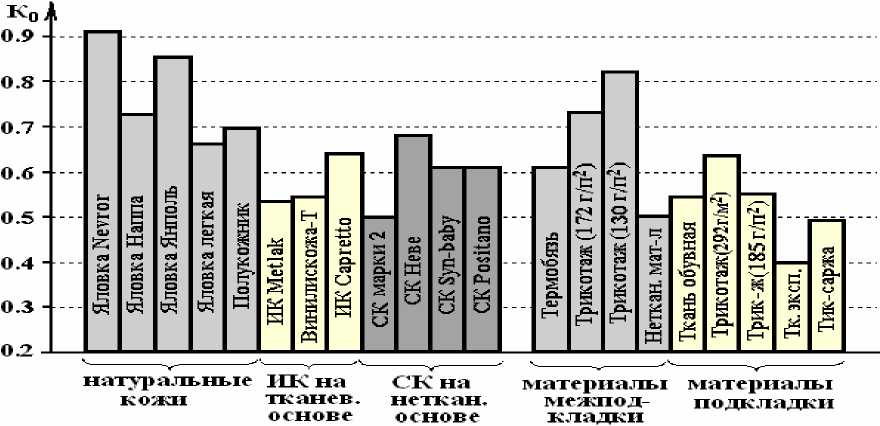
Рисунок 2 - Комплексный показатель упруго-пластических свойств материалов для верха обуви

Анализ полученных экспериментальных данных показал, что среди исследованных материалов для наружных деталей верха обуви наилучшим комплексом упруго-пластических свойств обладают натуральные кожи, среди текстильных материалов - трикотажные полотна. В системах материалов наиболее высокие значения комплексного показателя упруго-пластических свойств обеспечивают верх из яловки эластичной, межподкладка из термобязи и подкладка из ткани обувной.

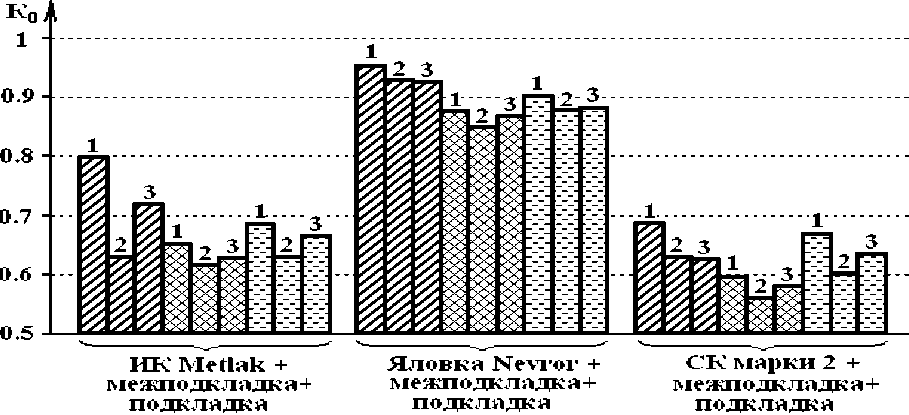
- верх + трикотаж (172 г/м ² ) + подкладка;

- верх + термобязь + подкладка;

ЕЗ - верх + нетканый материал + подкладка; 1 - верх+ межподкладка + ткань обувная; 2 - верх + межподкладка + трикотаж (292 г/м2); 3 - верх + межподкладка + ткань эксперим.

Рисунок 3 - Комплексный показатель упруго-пластических свойств систем материалов для верха обуви

В целях обеспечения рациональной комплектации пакетов верха обуви по показателю «приформовываемость верха обуви к стопе» с помощью множественного регрессионного анализа была установлена математическая зависимость между упруго-пластическими свойствами заготовки верха обуви и свойствами входящих в нее материалов следующего вида:

К о^с = 0,74 К о^в + 0,20 К о^{м / п} + 0,23 К о^п                   (12)

где К _о ^с , К _о ^в , К _о ^{м / п} , К _о ^п –комплексные показатели упруго-пластических свойств соответственно систем материалов для верха обуви, материалов верха, межподкладки и подкладки обуви.

Полученная математическая модель является адекватной, так как расчетный критерий Фишера превышает табличное значение, все коэффициенты уравнения значимы, так как имеют уровень значимости р < 0,05.

ВЫВОДЫ

С использованием метода главных компонент осуществлено сокращение размерности исходного признакового пространства и выявлены наиболее информативные показатели, характеризующие упруго-пластические свойства материалов и систем для верха обуви.

Рассчитаны комплексные показатели упруго-пластических свойств материалов и систем на основе наиболее информативных единичных показателей. Установлена математическая модель зависимости между комплексными показателями упругопластических свойств систем материалов и входящих в них комплектующих, позволяющая уже на стадии конструкторско-технологической подготовки прогнозировать свойства пакетов верха обуви.