Комплексный алгоритм обнаружения аномальных особенностей в природных временных рядах

Известной проблемой извлечения информации из данных в большинстве прикладных областей (физика, биология, медицина и др.) является высокая доля неполных априорных знаний об информационном сигнале и шуме. Процедуру выделения полезной информации из природных данных также существенно затрудняет наличие коррелированных шумов. Применение современных нейросетевых методов в некоторых случаях не обеспечивает требуемой точности решения данной задачи. Это связано с существенной нестацио-нарностью природных данных вследствие постоянной изменчивости природных процессов и отсутствием представительной выборки для обучения нейронных сетей. Указанные проблемы требуют усовершенствования методов обработки и анализа природных данных и создания новых более эффективных подходов и методов, в том числе с использованием нейросетевых технологий. Например, в работе [1] для решения задачи обнаружения аномалий в технологических сигналах авторами предлагается подход, основанный на комбинации ансамбля из базовых классификаторов на основе алгоритмов машинного обучения и вейвлет- преобразования. Применение вейвлет-коэффициентов на этапе формирования информативного признакового пространства для обучения классификаторов и консолидации прогнозов позволило повысить точность распознавания и повысить качество мониторинга объектов управления [1]. В работе [2] для задачи обнаружения ранних признаков отказов и поломок оборудования представлен подход к обнаружению аномалий в нестационарных технологических сигналах с использованием преобразования Гильберта–Хуанга совместно со статистической моделью классификации. Способность адаптации к нестационарным данным и высокая детализация в частотно-временной области подхода [2] позволила повысить точность обнаружения моделированных аномалий до 94%.

Задачи обработки и анализа природных данных, ввиду пассивности проводимых экспериментов, составляют еще большую сложность. Например, в работе [3], в области медицины, для оптимизации исследований головного мозга по данным функциональной магнитно-резонансной томографии (МРТ) предложена нейросетевая технология обнаружения ступенчатых аномалий с обучением на частично синтезированных данных с адаптацией на основе метаобучения.

Разработанная процедура формирования синтетического набора данных позволила существенно оптимизировать процедуру нейросетевого обучения [3]. Примером из области космофизики является работа [4], описывающая новый комбинированный метод выявления скрытых аномалий в вариациях галактических космических лучей (КЛ). Метод основан на совмещении спектрально-сингулярного разложения сигналов КЛ и вейвлет-преобразования. Как показано в работе [4], спектрально-сингулярное разложение сигналов КЛ позволяет изучить динамику вариаций, а вейвлет-преобразование позволяет вычислять энергию корот-копериодных вариаций произвольной формы (скрытых аномалий в КЛ) на фоне шума, превышающего по амплитуде полезный сигнал. В работах [5, 6] рассмотрены методы анализа природных данных для задач космической погоды. В частности, в работе [6] предложен автоматизированный метод анализа параметров ионосферы и обнаружения ионосферных аномалий на основе комплексного подхода, объединяющего методы вейвлет-преобразования с моделями авторегрессии – проинтегрированного скользящего среднего. На основе метода [6] исследователями обнаружены ко-роткопериодные аномальные изменения, предшествующие магнитным бурям и характеризующие возникновение колебательных процессов в ионосфере на фоне повышенной солнечной активности, что позволило авторам получить важный прикладной результат.

Объектом исследования являются алгоритмы анализа данных нейтронных мониторов (НМ), отражающих интенсивность вторичных космических лучей в околоземном пространстве [7]. В периоды повышенной солнечной активности в данных НМ наблюдаются аномальные особенности, обнаружение которых важно в задачах космической погоды [7]. Аномальные особенности в данных НМ возникают в случайные моменты времени и имеют разнообразную форму, что усложняет процедуру их обнаружения. Высокая доля неопределенности знаний о полезной составляющей данных НМ и их нестацио-нарность делает неэффективным применение классических методов анализа временных рядов (моделей ARIMA, методов декомпозиции временных рядов и т.п.). Применение методов машинного обучения, в частности нейронных сетей, требует периодической адаптации алгоритмов ввиду существенной изменчивости временного хода данных НМ. Это снижает их эффективность и не обеспечивает возможность получения результата в оперативном режиме.

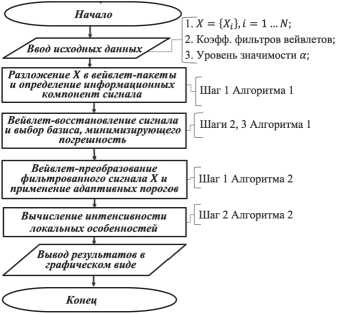
Учитывая структуру анализируемых данных, в работе предложен комплексный алгоритм обнаружения аномальных особенностей, основанный на синтезе вейвлет-преобразования с адаптивными пороговыми функциями. Методы вейвлет-преобразо-вания имеют обширный набор базисов разной формы и эффективны для анализа данных нестационарной структуры. Использование вейвлетов в работе позволило реализовать операции обнаружения и оценки параметров аномальных особенностей разной формы и длительности, в том числе резких всплесков, особенностей пикообразной формы и др. Компактный носитель вейвлетов обеспечил высокую степень локализации получаемой информации о моментах возникновения аномальных особенностей. Построенный комплексный алгоритм основан на разработанных авторами правилах, применение которых позволяет минимизировать погрешность оценки информационного сигнала. Предложенный алгоритм основан на теории, описанной в работах [6, 8], и включает в себя алгоритм определения информационных компонент сигнала и алгоритм адаптивной вейвлет-фильтрации сигнала. Алгоритм определения информационных компонент сигнала (алгоритм 1) подавляет шум, в том числе коррелированный, и определяет информационные составляющие сигнала. Алгоритм адаптивной вейвлет-филь-трации сигнала (алгоритм 2) путем комбинации дискретного вейвлет-преобразования и пороговых функций обнаруживает аномальные особенности и оценивает их интенсивность. Алгоритм 1 и алгоритм 2 являются законченными и могут быть применены независимо. В статье описаны операции комплексного алгоритма, представлена блок-схема его реализации. Показаны результаты применения комплексного алгоритма с использованием природных данных вторичных космических лучей и модельных данных, построенных по их подобию.

1.    Описание комплексного алгоритма

Регистрируемый сигнал рассматривается как комбинация

X [ t ] = F [ t ] + V [ t ],                                  (1)

где F [ t ] - полезный сигнал, F принадлежит пространству Гильберта H [9], V [ t ] – шум.

Выполняя разложение сигнала X в пространстве Н по базису B = { gm } _{m € N} (N - натуральные числа) и применяя пороговые функции, получаем:

F = £ П ( X , g_m ) g m ,                          (2)

meN где

, . I x , если I x | >  T ,

П ( x ) = \              -

• [ 0, если | x | <  T,

пороговая функция, 0 - скалярное произведение.

На основе операции (2) стоит задача подавить шум и выделить информационные компоненты сигнала. Погрешность оценки (2) для дискретного сигнала F [ tn ], tn € {1, • • •, N}, N — длина сигнала, есть r (F [tn ], F[ tn ]) = E{F [tn ]-X| tn ]2} =

= E ( E| F [ t - ] - X 1 1 - ]| ² 1 =                        (3)

l t n =1                               J

= ^{E J} E        I X I t n ] ^, g m I t n ]|² ’ ^,

[ t n e { t n :| X I t n ] , g m I tn ]|< T }

E – математическое ожидание, || || – норма в пространстве H.

Очевидно, погрешность (3) определяется абсолютными значениями коэффициентов |( X, g _m ) | разложения по базису и зависит от величины порога T.

Определение величины порога.

Применяя критерий отношения [10, 11] в окрестности O 8 [ t ]={ t n :| t n - t i l <  8 } некоторой точки t i , t i € {1,..., N}, будем иметь:

L ( ^X 1 1 . ] ) =

W ( X | t i ] / s i ) W ( X | t i ] / s о )

— T 8 ,

где L ( X [ t i ]) – функция правдоподобия, W ( X [ t i ] / s 0 ), W ( X [ t i ] / s 1 ) – плотности вероятностей при отсутствии (справедливости гипотезы Г 0 ) и наличии информационной составляющей сигнала (справедливости гипотезы Г 1 ) соответственно, s 0 , s 1 – возможные состояния сигнала, T 8 - величина порога в окрестности O 8 - некоторой точки t i .

Тогда, используя критерий Неймана–Пирсона [10, 11], для оценки порога Tа, 8 в окрестности O 8 точки t i с заданной доверительной вероятностью а будем решать следующую оптимизационную задачу:

| A W ( X | t i ] / s ₀ ) dX =а = const , J 0 W ( X 1 1 , .] / s 1 ) df =y^ max,

где а - заданная ошибка первого рода, у = 1 - Р - мощность критерия, Р - ошибка второго рода, A - критическая область.

Поскольку гипотеза Г 1 в рассматриваемой постановке задачи является простой альтернативой, можно рассматривать только гипотезу Г 0 , так как отклонение Г 0 означает принятие гипотезы Г 1 .

Тогда из соотношений (3) – (5) получаем следующее Правило определения величины порога (Правило 1) : порог Та, 8 в окрестности O 8 точки 1 ₀ с заданной доверительной вероятностью а будем определять, как

^Т а,8   ^Т а * ° 5 ,

где Т а - а -квантили распред. Стьюдента [11],

\ 1 2⁵ /                               -------------------------- \2

Й 5 = 2^ E (|X I tn ], gm I tn ]|-|X I tn ] , gm I tn ]|) - выборочное стандартное отклонение величины КX[tn], gm[tn])| в окрестности O8 точки ti,

| X I tn ], gm I tn ]| - среднее значение.

В случае разложения функции X [ t n ] по вейвлет-ба-зису [12, 13], формула (2) примет вид [6, 8]:

N

F I t n ] = EE n ( X I t n ] , T k , n I t n ] ) T k , n I t n ] ,          (7)

k n =1

где T _k , n I t n ] = 2 k ² T ( 2 k t - n ) - вейвлеты,

П ( X I t n ] , T k , n I t n ] ) =

XI tn ], T k,n 11 ], если | XI tn ], T k,n I tn ]| — Та,k, n , -0, если | XI tn ], T k,n I tn ]|< Та, k, n , пороговые функции, Та,k,n = Та • °k,n - пороги на масштабе k в окрестности O8 точки t = n.

Замечание 1. В операции (7) пороги Т а , k , n , следуя соотношению (6), оцениваются на масштабе k в окрестности O 8 точки t n . Адаптация порогов Т а , _k , n под изменяющиеся свойства сигнала позволяет подавить коррелированный шум.

Замечание 2. Попадание вейвлет-коэффициентов в критическую область A (см. соотн. (5)) означает принятие гипотезы Г 1 и, как показано в [8], в вейвлет-про-странстве обеспечивает обнаружение аномальных особенностей сигнала.

Погрешность r (F [tn ], FI tn ]) оценки F (см. (3)), очевидно, зависит от аппроксимирующего вейвлета (см. (6)). Следуя результатам [9], в вейвлет-базисе погрешность может быть оценена как rT (F [tn ], FI tn ]) =

= E min (| ^F I t n ] ’ ^T k , n I t n ]| ² ’ ( ° *, n ) ² k , n

Тогда, ограничив погрешность (8) величиной rT(F [tn ], FI tn ])< E П,n )2, k,n введем следующее правило определения наилучшего аппроксимирующего вейвлета (Правило 2).

Правило 2. Наилучшим аппроксимирующим вейвлетом Tmin для сигнала F будем считать вейвлет, удовлетворяющий условию rTmn (F [tn ],FI tn ]) = min E (°In )2’ k,n где Q - множество рассматриваемых вейвлетов,

Г] 25_/\ 2~

° I n = А Ь E (I X I t n ] , T k , n I t n ]| - 1 X I t n ] , T k , n I t n ]| ) .

V 28 n=1''

Табл. 1. Погрешности для разных вейвлетов

E „ К )2	Вейвлет-функция
X	coif_1	coif_2	coif_3	db_1	db_2	db_3
ст. Инувик	0,0175	0,0170	0,0176	0,0178	0,0174	0,0176
	0,0177	0,0175	0,0174	0,0178	0,0177	0,0173
ст. Оулу	0,0189	0,0187	0,0188	0,0190	0,0189	0,0188
	0,0202	0,0202	0,0201	0,0203	0,0200	0,0201
РН	6	12	18	2	4	6
ЧНМ	2	4	6	1	2	4

Замечание 3. В данной работе наилучший аппроксимирующий вейвлет определялся в рамках семейств Добеши и Койфлеты [12, 13]. Выбор семейств основывался на таких характеристиках вейвлетов, как гладкость, число нулевых моментов и размер носителя, обоснован в работе [14].

Результаты применения Правила 2 для вейвлетов семейств Добеши и Койфлеты представлены в табл. 1. Оценки выполнялись для вейвлетов порядков 1 – 3, с учетом допустимых размеров их носителей. Погрешности аппроксимации для разных вейвлетов рассчитывались по данным станций Инувик и Оулу в периоды высокой и низкой активности Солнца. В работе учитывались такие характеристики вейвлетов, как размер носителя (РН) и число нулевых моментов (ЧНМ).

Комплексный алгоритм анализа данных и обнаружения аномалий.

Алгоритм определения информационных компонент сигнала (Алгоритм 1):

Шаг 1. Используя базисы вейвлет-пакетов: W0 = ® I = ₀ W jp ,{ T j (2 j t - m )} _{m e H} , выполняем разложение сигнала и применяем пороговые функции, величины порогов определяем по правилу 1 :

Базис B jp¹ = { T P (2 j t - m )} _{m e N} пространства W jp есть базис

{Tj (2t-m )}meN , если Y\X, T P, m)l2 >    £    | (X, T2^ m ) F + E | (X, T 2^ } \2, me Ip                                me IP                                  me 12 P+1

j me N И— } me N s если £\{X,TP,m)\<      £      \ {x,T 2+1,m) p + E \

где множество индексов

I1, l = p, 2 p, 2 p +1, m e I1, если |X [ tn ] , TP m [ tn ]| > TP-m , TIP, j,m = T« ' 6P,m ■

Шаг 2. Выполняем вейвлет-восстановление преобразованного на основе шага 1 сигнала

JN

F [tn ] = EEn (X [tn ] , T^Pm [tn ]) T^P m [tn ] , j=0 m=1

где N – длина сигнала, J – наибольший масштаб.

Шаг 3. По правилу 2 определяем наилучший аппроксимирующий вейвлет Tmin ■ На выходе Алгоритма имеем вектор F_Tmin [t_n ] ■

Алгоритм адаптивной вейвлет-фильтрации сигнала (Алгоритм 2):

Шаг 1. Выполняем дискретное вейвлет-преобразование сигнала F_Tmin [t_n ] и применяем пороговые функции (величины порогов определяем по правилу 1):

N

F[tn ] = EEn(FTmn [tn ],Tk,n [tn])Tk,n [tn ], k n=1

П (Ftmn [tn ], Tk,n [tn ]) =

= j FTmn [ tn ] , ^Tk, n [ tn ] , если | FTmn [ tn ] , ^Tk, n [ tn ]|>To, k, n

I          0, если |Ftmn [tn ], Tk,n [tn ]|< T_a,k,n

To,k,n = ^ * 6k,n - пороги.

Полученный преобразованный сигнал F [t_n ] содержит аномальные особенности.

Шаг 2. Оцениваем суммарную интенсивность выделенных аномальных особенностей:

K

E [tn ] = ЕП(FTmn [tn ],Tk,n [tn])■ k=0

Замечание 4. Для обеспечения оперативности получения результата алгоритма и сокращения времени его выполнения в шаге 1 Алгоритма 1 использовался предварительно определённый по Правилу 2 набор вейвлет-функций (см. табл. 1).

На рис. 1 представлена блок-схема предлагаемого комплексного алгоритма.

Рис. 1. Схема реализации комплексного алгоритма

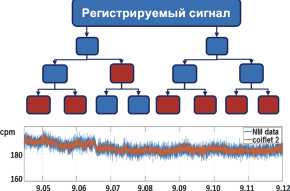
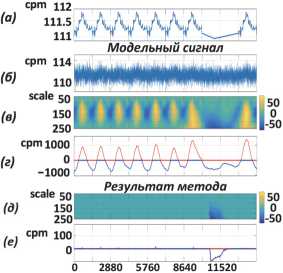
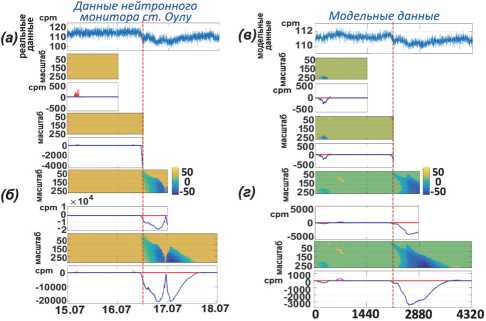
2.    Результаты применения алгоритма

В работе использовались природные данные вторичных космических лучей [15] и модельные данные, построенные по их подобию. Вторичные космические лучи – это частицы высоких энергий, регистрируемые наземными станциями нейтронных мониторов [15].

Аномальные изменения в потоке вторичных космических лучей свидетельствуют о возмущениях в околоземном космическом пространстве, которые способны нарушить работу систем спутниковой, навигационной и радиосвязи, а также повысить риск обострения сердечно-сосудистых заболеваний людей [7, 16]. Аномальные изменения в космических лучах могут проявляться в виде так называемых Форбуш-эффектов (внезапное локальное снижение интенсивности космических лучей) [17] и GLE-событий (сильное локальное возрастание интенсивности космических лучей, регистрируемых на поверхности Земли) [18].

На рис. 2 представлен пример дерева вейвлет-паке-тов, построенного по алгоритму определения информационных компонент сигнала. Красным цветом отмечены выбранные информационные узлы. Ниже, на рис. 2, синим цветом показан исходный сигнал, оранжевым – результат данного алгоритма. Результат подтверждает нестационарную структуру регистрируемых данных вторичных космических лучей и наличие шума.

Сентябрь 2014

Рис. 2. Результат алгоритма 1

На рис. 3 показан результат обнаружения малоамплитудной продолжительной аномальной особенности (отношение сигнал / шум 1.1) в построенном модельном сигнале на фоне коррелированного шума (добавлен аддитивный розовый шум). Обнаружение выполнено на основе применения операции непрерывного вейвлет-преобразования (НВП) (рис. 3в, г) и на основе предложенного комплексного алгоритма (рис. 3 д, е). Следует отметить, что аномальная особенность в зашумленном модельном сигнале не видна (рис. 3б). Полученный результат показывает, что ввиду наличия коррелированного шума её обнаружить на основе непрерывного вейвлет-преобразования невозможно. Предложенный алгоритм позволил подавить шум и обнаружить аномальную особенность.

На рис. 4 представлен пример применения комплексного алгоритма к данным нейтронного монитора ст. Оулу за 15–18 июля (слева) и модельным данным (справа), содержащим аномальную особенность. В модельный сигнал добавлялись аномальные особенности вида треугольный импульс с отношением сигнал /шум = 1,5. Момент регистрации Форбуш-эффекта в природных данных [19] и добавленная аномальная особенность в модельные данные отмечены красными пунктирными вертикальными линиями. Результаты комплексного алгоритма представлены по мере поступления данных в систему обработки. Результат алгоритма подтверждает его эффективность как для модельных, так и для природных данных. Алгоритм позволил обнаружить аномальную особенность своевременно.

Рис. 3. Результаты обработки: (а) тренд+аномалия; (б) тренд+аномалия+шум; (в, г) результат применения НВП; (д, е) результат применения комплексного алгоритма

Рис. 4. Результат обработки: (а) данные нейтронного монитора ст. Оулу; (б) результаты применения комплексного алгоритма к данным нейтронного монитора (обработка выполнена по мере поступления данных в систему обработки); (в) модельные данные, построенные по подобию природных; (г) результаты применения комплексного алгоритма к модельным данным (обработка выполнена по мере поступления данных в систему обработки)

В табл. 2 представлен расчет временных затрат на работу комплексного алгоритма. Расчет выполнен в зависимости от объема входных данных. Реализация комплексного алгоритма выполнена в программе, написанной на языке Java в среде разработки IntelliJ IDEA 2020.3.4 [20]. Временные затраты позволяют применять алгоритм в оперативном анализе данных нейтронных мониторов.

Табл. 2. Временные затраты на работу комплексного алгоритма (мкс)

Операции	Объем входных данных (отсчеты)
	N=2880  N=4320		N=5760
	Среднее время, мкс
Вывод результата программы	75,45	109,78	127,05

Заключение

Результаты исследования показали эффективность предложенного комплексного алгоритма для анализа природных данных и обнаружения аномальных особенностей разной формы и продолжительности. Применение алгоритма позволило обнаружить аномальную особенность малой амплитуды (отношение сигнал / шум 1.1) на фоне коррелированного шума. Данный результат свидетельствует о высокой эффективности разработанного алгоритма. Выполненный расчет временных затрат на выполнение алгоритма показал возможность его применения в режиме, близком к реальному времени, что важно для задач космической погоды.

Работа выполнена за счет Государственного задания ИКИР ДВО РАН (рег. № темы 124012300245-2).