Комплексный анализ как инструментарий в решении электроэнергетических задач

Введение. Математические методы широко используются в энергетике, являясь неотъемлемой частью процессов и технологий, связанных с производством, передачей и распределением энергии. Она помогает улучшить эффективность работы энергетических систем, оптимизировать расходы и улучшить устойчивость энергетического сектора.

Цель написания  научной статьи:  рассмотреть вопрос использования комплексного анализа при решении электроэнергетических задач.

Задачи:

• 1.    Изучить вопрос использования математического моделирования;

• 2.    Изучить вопрос использования переменного тока;

• 3.    Выявить особенности изменения тока синусоидальной формы;

• 4.    Рассмотреть комплексный анализ как инструмент для решения электроэнергетических задач;

• 5.    Рассмотреть формы комплексных чисел.

Основная часть

Одной из важных областей, где математика применяется в энергетике, является моделирование и оптимизация энергетических систем. Математическое моделирование позволяет создавать абстрактные модели энергетических систем и изучать их поведение в различных условиях. Это позволяет инженерам и ученым оптимизировать работу энергетических систем, прогнозировать и устранять возможные проблемы и увеличивать эффективность процессов.

Например, математическое моделирование может быть использовано для оптимизации распределения энергии в электросетях. Модели могут учитывать множество факторов, таких как потребление электроэнергии, распределение нагрузки, пропускная способность линий передачи, а такжевозможные аварийные ситуации.[1,9] Математические алгоритмы могут использоваться для определения оптимальной схемы распределения и минимизации потерь энергии (рис.1).

Рисунок 1 – Энергетическая модель объекта

Еще одна важная область математики в энергетике – прогнозирование производства энергии. Энергетические системы часто зависят от изменяющихся условий, таких как погода, сезонность и изменение потребления энергии. В этом случае математические модели и статистические методы могут быть использованы для прогнозирования будущего спроса на энергию и оптимизации производственных мощностей [5, 6]. Это помогает энергетическим компаниям лучше планировать свою работу и избегать перепроизводства или недостаточного обеспечения потребности в энергии.

В электроэнергетике переменный ток имеет важное значение. Это можно объяснить тем, что многие электроустановки работают с помощью переменного тока, который меняется синусоидально.

Сумма и разность синусоидальных величин возможно поменять на векторы. Не считая сложения и вычитания, синусоидальные величины надо делить и умножать. И тут нам помогают комплексные числа.

В большинстве случаев комплексные числа употребляются в цепях переменного тока, т.к. этот ток очень часто меняет свою величину и направление. Самая распространённая форма этого тока – синусоидальная. Применение синусоидальных величин является основным методом, изучаемым в ТОЭ («Теоретических основах электротехники») (рис. 2).

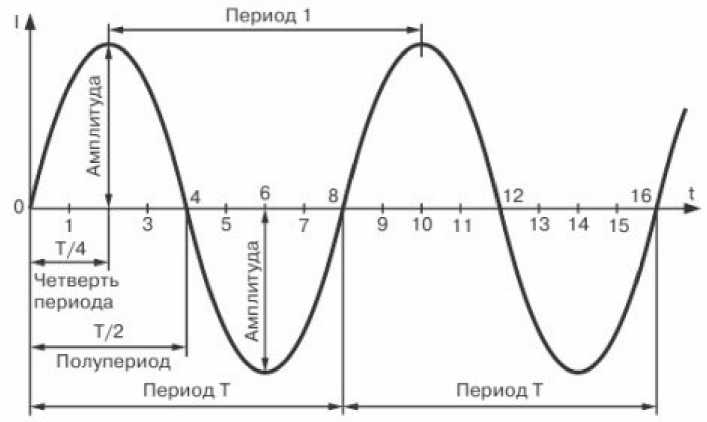
Рисунок 2. – Синусоидальная форма переменного тока

В электротехнике «Переменный ток» является одной из значимых тем. Электрические станции вырабатывают скалярное напряжение, сформировывающее в обычных электромагнитных цепях скалярный ток, но гидроэлектростанции создают перенапряжение и ток не простопеременный, а меняющийся синусоидально.

Синусоидальная форма тока широко применяется в различных областях, таких как электроэнергетика, электротехника, электроника и др. Она позволяет точно представить изменение тока в цепи и упрощает расчеты и проектирование электрических систем и устройств.

Она характеризуется тем, что ее величина меняется по синусоидальному закону, а ее направление меняется согласно своим математическим правилам. Такое изменение тока обусловлено изменением напряжения в электрической цепи во времени.

Изменение тока синусоидальной формы имеет следующие особенности:

• 1.    Амплитуда – это максимальное значение тока, которое достигается в каждом положительном или отрицательном полупериоде колебаний. Амплитуда тока обычно обозначается буквой "I" и измеряется в амперах (А).

• 2.    Частота – это количество полных колебаний тока, которое происходит за единицу времени. Частота тока обычно обозначается буквой "f" и измеряется в герцах (Гц). В случае синусоидальной формы тока, частота остается постоянной на протяжении всего времени.

• 3.    Фаза – это смещение начала колебаний тока относительно определенной точки во времени. Фаза тока обычно измеряется в градусах или радианах и может быть положительной или отрицательной [10].

Синусоидальная форма тока широко применяется в различных областях, таких как электроэнергетика, электротехника, электроника и др. Она позволяет точно представить изменение тока в цепи и упрощает расчеты и проектирование электрических систем и устройств.

Комплексные числа используются при измерении сопротивления – умения объекта сопротивляться прохождению через него электромагнитного тока. А мнимые числа применяют для измерения индукции ёмкости.

Использование комплексных чисел позволяет применить законы, теоремы и методы расчетов, которые применяются в цепях постоянного тока, для расчета цепей переменного электротока.

Комплексный анализ – это математический инструмент, который широко применяется в решении электроэнергетических задач. Он основан на теории функций комплексного переменного и позволяет анализировать и моделировать различные процессы, связанные с электроэнергетикой.

Одной из основных проблем, с которыми сталкиваются инженеры в электроэнергетике, является расчет и анализ электрических цепей. Комплексный анализ позволяет решать такие задачи более эффективно, чем традиционные методы. Он позволяет представить переменные и параметры электрической цепи в виде комплексных чисел, что упрощает анализ и моделирование электрических систем.

Одним из наиболее известных применений комплексного анализа в электроэнергетике является расчет и анализ переменных токов и напряжений в электрических сетях. Комплексные числа позволяют представить переменные токов и напряжений как фазы, содержащие информацию о амплитуде и фазе этих переменных. Такое представление упрощает решение уравнений, связанных с электрическими сетями, и позволяет более точно анализировать их характеристики.

Еще одним применением комплексного анализа является расчет и анализ электрических машин, таких как генераторы, трансформаторы и динамо-машины. Комплексные числа позволяют описать работу этих устройств с точки зрения переменных токов и напряжений. Это позволяет определить их электрическую мощность, коэффициенты полезного действия и другие характеристики [8, 10].

Кроме того, комплексный анализ используется для моделирования и анализа электрических схем и систем управления.

Это позволяет определить стабильность и надежность работы таких систем, а также оценить их эффективность и энергопотребление.

Комплексный анализ также применяется в решении задачи синтеза электроэнергетических систем, таких как электроэнергетические сети и системы передачи электроэнергии. Он позволяет оптимизировать работу таких систем, учитывая различные факторы, такие как нагрузка, расход энергии и стоимость (табл. 1).

Комплексный анализ является мощным инструментом в решении электроэнергетических задач. Он позволяет эффективно моделировать и анализировать различные процессы, связанные с электроэнергетикой, и оптимизировать работу электроэнергетических систем. Дальнейшее развитие этой области математики обещает более точные и эффективные методы решения задач в электроэнергетике. Синусоидальная форма тока – это одна из форм взаимозависимости, которая описывает изменение электрического тока во времени.

Она является одной из наиболее распространенных форм взаимозависимости тока и позволяет точно представить его величину и направление на различных этапах.

Таблица 1 – Комплексный анализ основных показателей электростанций

Типы электростанций	Удельные капиталовложения		Себестоимость производства энергии
	р./кВт	%	коп./кВт^ч	%
ТЭЦ	2500	170	10	74
КЭС	1500	100	12-15	100
ГТУ	4000-7000	270-470	20-40	150-300
АЭС	2000-3000	130-200	12-15	100
ГЭС	7000-10000	470-670	1-5	7-37
Прочие типы, в т.ч.:	5000-20000	330-1300	100-1000	740-7400
солнечные термические	4500-6000	300-400	23-28	170-210
полупроводниковые	3700-6500	250-430	22-30	160-220
геотермальные	2500-3200	160-210	23-30	170-220

На данный момент большинство задач в электроэнергетике не могут решиться без комплексных чисел. Эти числа – важная часть электроэнергетики (рис. 3).

z=x+i·y – алгебраическая форма записи комплексного числа, где i= V-1, x – действительная часть комплексного числа, y – мнимая часть комплексного числа.

Z= |z| •eiФ- показательная форма записи комплексного числа, где |z| = д/x2 + y2 - модуль комплексного числа,

( у I

Ф = arctg I I - аргумент комплексного числа.

V x )

Z= |z| • (cos(ф) + i • sin(ф)) - тригонометрическая форма записи комплексного числа, где x= |z| • соз(ф), y= |z| • sin(ф),

Рисунок 3 – Представление комплексного числа в алгебраической, тригонометрической и показательной форме

Кроме того, математика играет важную роль в развитии и исследовании новых источников энергии и технологий. Математические модели и алгоритмы могут быть использованы для анализа и оптимизации работы солнечных панелей, ветряных турбин, гидроэлектростанций и других возобновляемых источников энергии [2, 7]. Они могут помочь ученым и инженерам создать более эффективные системы, учитывающие такие факторы, как колебания и нестабильность производства энергии из возобновляемых источников.

Заключение .

По мнению авторов, математические методы играют неотъемлемую роль в энергетической отрасли. Она помогает оптимизировать работу энергетических систем, прогнозировать и анализировать производство энергии и разрабатывать новые источники энергии и технологии [3, 4] Без математики энергетика не смогла бы достичь таких высоких уровней эффективности и устойчивости, какие существуют сегодня.