Комплексный подход к оценке имущественных отношений между экономическими субъектами Российской Федерации (микро- и мезоэкономические аспекты)

Опыт проведения псевдореформ либерального фундаментализма (90-е годы XX века) обусловливает необходимость первоочередного подъема реального отечественного производства и «вливание» в него значительных инвестиций. Стратегия экономического развития страны сформулирована – удвоение валового внутреннего продукта (ВВП) России в течение десяти лет [1]. Это объективно сопряжено с различного рода рисками, методы математического моделирования управления которыми находятся в постоянном поле зрения исследователей (Багриновский (1977, 1998, 1999, 2003), Горбатов (2000), Гурвич и др. (2001), Замков и др. (1998), Качалов (1997, 2002), Клейнер (1997, 2001, 2002), Тамбовцев (1997), Хачат- рян (2002), Шелобаев (2001),…2. Стратегия экономического роста ставит на приоритетное место повышение инвестиционной активности и продуктивное ее обслуживание фундаментальными теоретическими и практическими разработками отечественных и зарубежных ученых в специфическом разделе экономической науки – оценка эффективности инвестиционных проектов (Бочаров (2002), Виленский (1998, 2002), Виноградов (2002),Земляков (2004), Ивашкевич (2002), Ковалев (2000), Коссов (2000), Круш-виц (2000), Лившиц (1971, 1984, 1998, 1999, 2000, 2002), Смоляк (1998, 2001, 2002), Фельдман (2002), Шахназаров (2000),…). Статистика на стороне такого подхода: по различным оценкам, чистый приток в Россию прямых иностранных инвестиций составил в течение последних лет всего лишь 2 млрд долларов США в год [3, с. 6]. Инвестиции в современной России восстанавливаются после кризиса 1990-х годов намного медленнее, чем ВВП. За 9 месяцев 2003 года из России частным сектором вывезено 19,6 млрд долл. Реальные объемы вывезенного из России капитала превышают 300 млрд. долл. [12, с. 82]. По-видимому, одной из немаловажных причин, останавливающих потенциальных инвесторов, является то, что представляемые им инвестиционные предложения не содержат убедительных обоснований их высокой эффективности в условиях повышенного риска [14, с. 13]. Мировой опыт свидетельствует, что высокий риск (социальный и экономический) обычно не останавливает предприимчивых инвесторов, если они уверены, что с учетом риска бизнес будет достаточно эффективным. С другой стороны, явно сохраняется неумение кредитных учреждений отбирать эффективные инвестиционные проекты и реализовать их на практике.3 Проблемы и задачи теории эффективности реальных инвестиционных проектов наиболее полно обоснованы и доказаны для российских условий в лучших монографиях отечественных ученых [13, 14, 26, 27, 32 и др.]. Главные специалисты страны в области оценки эффективности инвестиционных проектов, разработки программного обеспечения для соответствующих расчетов и их (оценок) экономико-математического моделирования, обобщая свой многолетний научный и практический опыт, сформулировали первоочередные нерешенные задачи и направления важнейших дальнейших исследований, а именно:

• •    более адекватный учет специфики российской переходной экономики при определении содержания и структуры системы критериальных показателей;

• •    совершенствование способов учета риска и неопределенности;

• •    учет обратного влияния результатов исследования на макроэкономические показатели и параметры [14, с. 876–877].

Особое внимание специалисты обращают на то, что отбор проектов (или вариантов проекта) существенно осложняется, если проекты предполагают наличие многих участников [14, с. 541]. Этот аспект и станет предметом нашего исследования.

Постановка задачи

В основе нашего исследования лежат оценки эффективности инвестиционных проектов, полученные по величине их интегрального дисконтированного эффекта (далее эффекта), рассчитываемого как разность между дисконтированными доходами и расходами, связанными с реализацией каждого проекта. Этот показатель (эффект) играет роль критерия: проекты с положительным эффектом рассматриваются как эффективные, проекты с отрицательным эффектом – как неэффективные, а при наличии нескольких альтернативных проектов (или вариантов проекта) луч- шим считается тот, у которого значение эффекта будет больше. Важной особенностью этого показателя (эффекта) является его аддитивность – при одновременной реализации независимых проектов доходы и расходы по ним, а следовательно, и эффекты суммируются. Мы не будем останавливаться на методике и особенностях расчета этого показателя и адресуем читателя к соответствующей литературе [4, 14, 33]. Отметим лишь тот факт, что в нашем исследовании инвестиционная программа (базовый инвестиционный портфель как основа для формирования ОИП) составляется как по этой методике, так и на основании практических наработок ученых. В целине нерешенных задач, о которых сказано выше, градиент нашего исследования направлен на создание механизма эффективного использования рыночных элементов хозяйствования и оценок инвестиционных проектов в организации процедур планирования и управления распределительными отношениями в инвестиционном процессе, т. е. результаты комплексного подхода к оценке эффективности инвестиционных проектов переносятся в сферу распределительных отношений внутри коллективного инвестора. В исследовании отбор проектов коллективным инвестором из инвестиционной программы достигается экономикоматематическими методами и моделями из различных ветвей неконтинуальной математики: линейной алгебры, теории вероятностей и математической статистики, эконометрики, теории графов, исследования операций и методов оптимизации, моделирования экономических систем и логистики. Базовые виртуальные схемы нашей концепции формирования ОИП показаны с помощью неориентированных графов на рисунках 1, 2а, 2б.

Разновидности моделей в инвестиционной сфере деятельности

Инвестиционная деятельность предприятия состоит из двух этапов:

• •    формирование инвестиционного портфеля;

• •    реализация инвестиционных проектов.

На рисунке 0.1 схематично показано место инвестиций в экономике предприятия.

Само предприятие здесь фигурирует как микросреда . Параметры микросреды отражают состояние предприятия и его производственные возможности.

Экономическая обстановка в стране, регионе, отрасли или на рынке сбыта продукции обозначена на рисунке 0.1 как макросреда . На основе анализа состояния макросреды, т. е. внешних для предприятия факторов, формируются экономические прогнозы ее развития: долгосрочные и краткосрочные.

Использование моделей при планировании инвестиций позволяет уменьшить неопределенность и риск, связанные с инвестиционной деятельностью.

Суть инвестиционного моделирования состоит в создании целостной системы подходов, моделей и методов, на основе которой конкретное предприятие, осуществляющее свою деятельность в неопределенных условиях внешней среды, может сформировать ОИП.

Создание такой системы предполагает решение следующих основных задач инвестиционного моделирования:

• 1)    выявление целей инвестиционной деятельности и построение системы критериев, оценивающих степень достижения этих целей;

• 2)    создание модели внешней среды, включающей в себя основные характеристики среды, их взаимосвязь и возможные будущие состояния;

• 3)    разработка модели обобщенного инвестиционного проекта, описывающей основные характеристики проектов, их взаимосвязь, а также связь с внешней средой и с системой целевых критериев;

• 4)    разработка системы ранжирования и отбора проектов для инвестиционного портфеля предприятия в условиях ресурсных ограничений.

На основе решения этих задач формируется ОИП предприятия. Конкретная модель формирования инвестиционного портфеля может иметь различные формы. Наиболее наглядной, на наш взгляд, является матричная форма модели в сочетании с моделью на основе двудольного графа, которые в симбиозе дополняются имитационным моделированием. В таблице 0.1 в сокращенном виде представлен анализ моделей принятия инвестиционных решений.

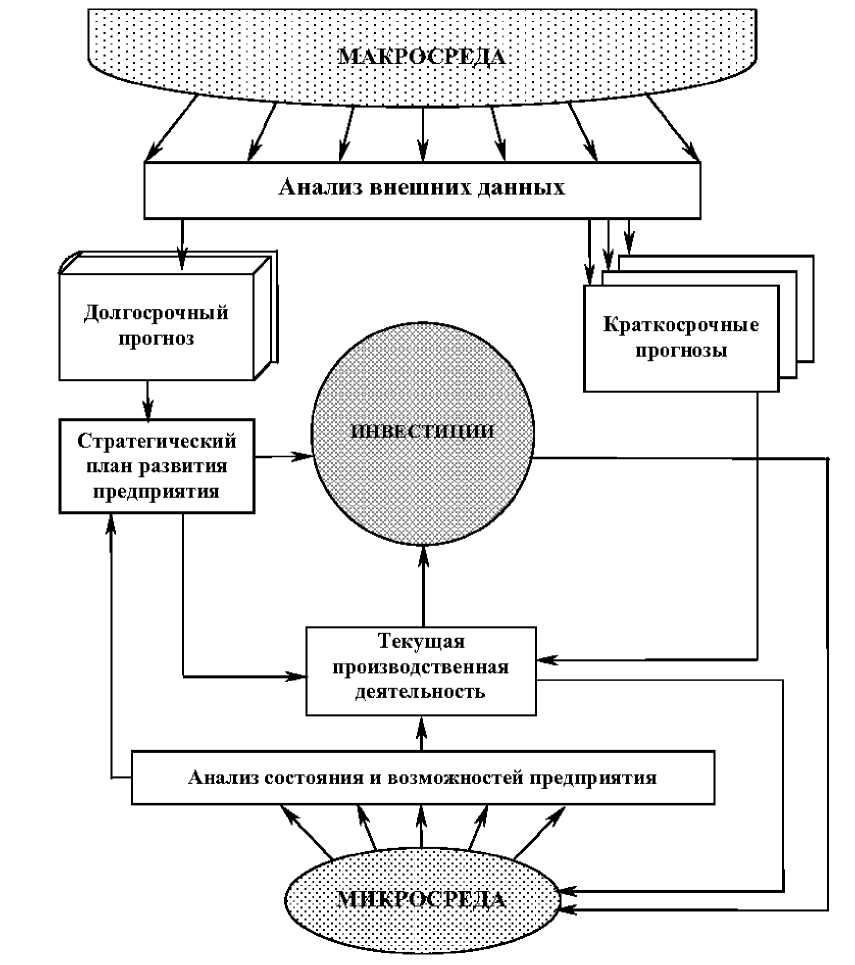
Рис. 0.1. Место инвестиций в экономике предприятия Источник: [ Виноградов Г.В. : 16, c. 210]

Таблица 0.1

Признаки моделей принятия инвестиционных решений

\Макросреда Критерии	Специфика проявления
	Определенность	Неопределенность
Техника решения	Единичное или программное	Единичное и/или программное
Альтернативы	Абсолютная Относительная Срок выгода       выгода         эксплуатации	Полная неопределенность	Ситуация риска	Неясность
Цели	Одна цель	Несколько целей
Аспект времени	Статические модели Динамические модели	Динамические модели
		Одноступенчатые	Многоступенчатые
			жесткие	гибкие

Источник: [ Шелобаев С.И. : 36, c. 251]

Вербальная модель распределительных отношений в инвестиционном процессе

В настоящее время в процессе управления, особенно на уровне мезоэкономики (региональный, межотраслевой рынки), когда в составе субъекта (производственное объединение, холдинг, трест, … далее – ПО) имеются дочерние предприятия (ДП), с которыми ПО как «мозговой» центр, наделенный статусом приоритетного инвестора, готово разделить риски в инвестиционной деятельности, ПО постоянно сталкивается с задачей отбора новых инструментов и анализа возможности их включения в формирование оптимального инвестиционного портфеля (ОИП) в режиме логистического подхода (учета интереса всех инвесторов). Если ранее (90-е годы XX века) ПО автономно формировало ОИП, т. е. решало задачу оптимизации собственных инвестиционных потоков на базе множества финансовых активов [рис. 1], то теперь, когда разгосударствление экономики по сценарию псевдореформаторов стало призрачным, ПО заинтересовано в оптимизации совмещенных инвестиционных потоков: как ПО, так и ДП с продуктивным разделением ответственности по рискам . В этом случае схема, показанная на рисунке 1, видоизменяется (усложняется), трансформируясь в два варианта, что и отражено на рисунках 2а и 2б, где пунктирные линии отображают функциональную связь ДП с ПО и их разделенную (автономную) ответственность по рискам, а сплошные линии – структуру потенциальных инвесторов (неориентированные графы G). Наиболее сложным и интересным, с точки зрения экономического содержания и математического моделирования, представляется комбинированный вариант (рис. 2б), особенностью которого является следующее:

• •    больше степеней свободы у ДП (отсутствует фактор психологического влияния ПО);

• •    приоритетный инвестор (ПО) «подстраховывает» ДП (дополнительное снижение риска);

• •    повышается мотивация ДП к коллективному участию в инвестиционной деятельности ПО;

• •    улучшается качество анализа инвестиционных проектов и/или фондовых рынков (в режиме перекрестных аналитических схем);

• •    солидарная ответственность за принимаемые решения становится прагматически обусловленной, а не декларативной;

• •    совершенствуется организация мышления лиц, принимающих решение (ЛПР), и их мотивация к творческому поиску на основе математического моделирования;

• •    повышается интеллектуальная «планка» мозговых (генерирующих) центров экономических субъектов;

• •    улучшаются качественные представления об исследуемой реальности (предпочтения ЛПР, наполняются конструктивностью и осознанной необходимостью применения методов имитационного моделирования);

• •    возрастает количество производных эффектов и т. д.

В целях адаптации предложенных схем к реальной действительности примем за аксиому следующее утверждение : ПО как приоритетный инвестор может направлять свои инвестиционные потоки любому (и необязательно единственному) эмитенту, а ДП – единственному , но любому эмитенту. Такая аксиоматика , во-первых, конкретизирует алгоритмы подсчета всех дуг неориентированных графов G , во-вторых, делает само исследование более востребованным и восприимчивым и, в-третьих, обеспечивает логический переход от вербального моделирования к экономико-математическому . Алгоритмы подсчета всех вариантов базовых инвестиционных портфелей (БИП) (рис. 1, 2а, 2б) покажем на условном примере.

Для случая, когда инвестиционная программа, сформированная по оценкам эффективности инвестиционных проектов [13, 14], состоит из 10 (десяти) эмитентов, а количество потенциальных инвесторов в совмещенных вариантах (рис. 2а, 2б) равно 5 (пяти), каждому варианту (рис. 1, 2а, 2б) соответствует свой максимальный набор базовых инвестиционных портфелей (число их различных комбинаций, К ):

• •    по традиционной схеме (рис. 1) К = 1 024;

• •    по современной схеме: (рис. 2а) К = 30 240;

(рис. 2б) К = 6 064.

Алгоритмы подсчета числа различных комбинаций и примеры их подсчета с применением основных правил и формул комбинаторики, а также свойства треугольника Паскаля приведены в таблицах 1 и 2, а условные сокращения – в пояснениях к рисункам 1, 2а, 2б в заключительной части статьи⁴.

На практике любой специалист с помощью треугольника Паскаля без труда и использования персонального компьютера вычислит биноминальные коэффициенты Cnk (читается: «Ц» из «н» по «к»), которые являются нижними элементами строки и получаются в результате сложения двух эле- ментов верхней строки, стоящих правее и левее его (нижнего элемента). В качестве основы берется треугольник из трех единиц I 1

• ^ 1 1 ) Возможен и другой алгоритм подсчета, если запомнить свойство разложения по формуле Ньютона: сумма биноминальных коэффициентов С П разложения ( x + aУ в общем виде записывается как равенство

С П + с П + с П + _ + с п ² + c n ^-1 + с п = 2 ^П .

Теперь перейдем к комбинированному математическому моделированию оптимальных и рациональных структур инвестиционного портфеля на примере конкретной задачи, что поможет заинтересованному читателю продуктивно руководствоваться настоящей статьей в своей повседневной деятельности .

Традиционная схема формирования ОИП одним инвестором (90-е годы XX века)

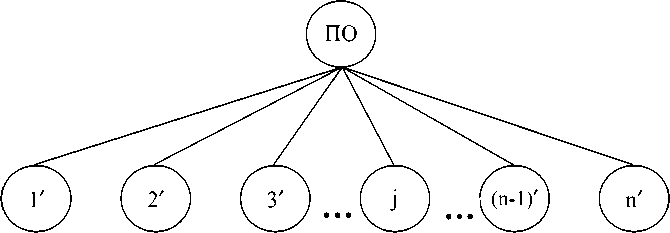
Рис.1. Базовый неориентированный граф G для формирования ОИП в узком смысле

Инвестор (ПО) единственный

Эмитенты (множество финансовых активов, J) j = Г-нт', j е J

Современные схемы формирования ОИП коллективным инвестором (начало XXI века)

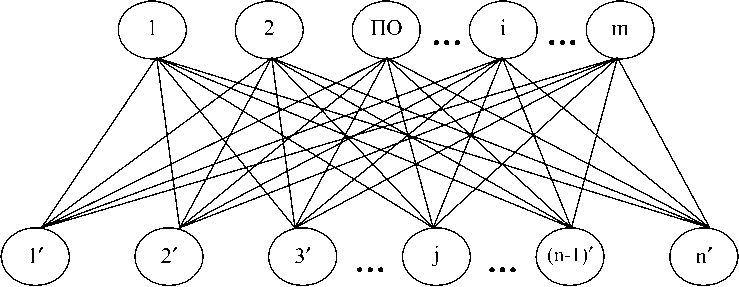
Инвесторы (множество потенциальных участников инвестиционной сферы деятельности ПО, I) i = 1ч-т, i е I

Эмитенты (J)

Рис. 2а. Базовый неориентированный граф G для формирования ОИП в широком смысле (абсолютно совмещенный вариант)

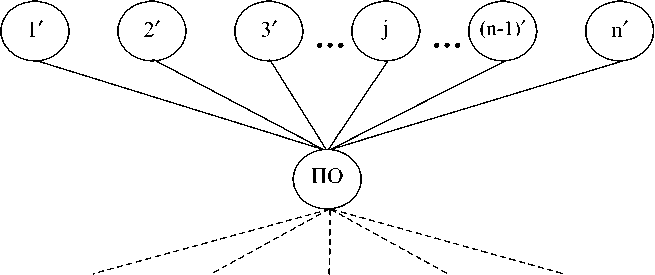
^^™ Эмитенты (J)

Инвестор (ПО) приоритетный

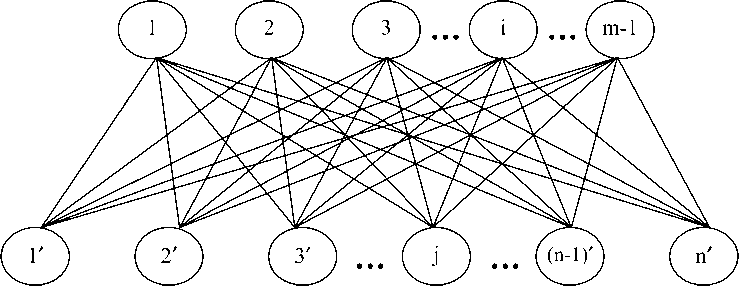
Рис. 2б. Базовый неориентированный граф G для формирования ОИП в широком смысле (относительно совмещенный вариант)

Инвесторы (ДП) i = 1+(m-1), i е I

Эмитенты (J)

Таблица 1

Алгоритмы подсчета различных комбинаций инвестиционных портфелей

Модели теории графов формирования инвестиционных портфелей	Формулы комбинаторики
	к=0	А™	^Г + £Сп к=0
Рис. 1	+
Рис. 2а		+
Рис. 26			+

где n – количество финансовых активов (эмитенты); m – количество потенциальных инвесторов (дочерние образования и ПО); k – количество предпочтений ПО, к = 0 + n ; Cnk – число сочетаний из n элементов	m A n – число размещений из n элементов по m равно A mm =         = n ( n - 1)( n - 2) - ( n - m + 1). ( n - m )! 4---------------- v---------------- ^ m сомножителей
по k равно Ck _ n!    _ n ( n - 1)( n - 2) ^ ( n - m + 1) , n = к !( n - к )! =         1 x 2 x ...x к         ’	По определению     n! = 1 x 2 x 3 x _ x n 0! = 1, c n = 1, c n = 1.

Таблица 2

Примеры подсчета различных комбинаций инвестиционных портфелей (n=10, m=5, k=0 + 10)

Модели теории графов формирования инвестиционных портфелей	Алгоритмы	Общее количество комбинаций
Рис. 1	Треугольник Паскаля 1 1      1 1    2    1 13 3 1 1    4   6   4   1 1   5 10 10 5   1 1   6  15 20  15  6   1 1 7 21 35 35 21 7 1 1   8  28 56 70 56 28  8 1 1   9 36 84 126 126 84 36 9 1 1 10 45 120 210 252 210 120 45 10 1 z^0 z^1 z>2 z>3 z^4 z>5 z>6 z^7 z>8 z^9 z^10 °10 u10              °10 °10 ^10     U10 °10 к = 1 + 10 + 45 + 120 + 210 + 252 + 210 +120 + 45 + 10 + 1 = 2п	1 024
Рис. 2а	Правило произведения комбинаторных задач А™ =10x9x8x7x6 = 30 240	30 240
Рис. 26	А™"1 + ^С„ =10x9x8x7 + 1 024 = 5 040 + 1 024 = 6 064 к=0	6 064