Комплексный подход к оценке имущественных отношений между экономическими субъектами Российской Федерации (микро- и мезоэкономические аспекты)

Теория прогресса Хокинса

Уйти нам трудно от мирских забот, Но Вечность постигает только тот, Кто на шаг сойдет с тропы привычной И путь продолжит от других отличный.

Авицена (Абу Али Ибн Сина, ок. 980 – 1037 гг.)

Переход от оценки эффективности инвестиционных проектов к моделям и алгоритмам теории графов

Развивая применение оценок эффективности инвестиционных проектов ², перейдем к изучению зависимостей оптимального инвестиционного портфеля (ОИП) и структуры потенциальных инвесторов от изменения условий состояния макросреды. Для решения задач, обусловленных такой зависимостью, воспользуемся математическими моделями и методами в логистике из теории графов (алгоритмы Егервари и Гросса) . В целях сопоставимости количественных результатов по выбранным функционалам (критериям) не будем менять базу исходных данных A (i, j) для всех состояний макросреды. Составим вербальную модель действительного хода инвестиционного процесса с помощью определенной системы понятий и ограниченного набора показателей. Условное производственное объединение (ПО), состоящее из пяти дочерних предприятий (i = 1 ^ 5, i е I), сформировало по тендерам эмитентов инвестиционную программу из шести финансовых активов (j = 1 ^ 6, j е J) со следующими, «плавающими по времени», объемами инвестиций (I) млрд р.:

j ~ 1 ^ 5 < I < 13;

j ~ 2 ^ 3 < I < 12;

j ~ 3 ^ 4

j ~ 5’ ^ 6 < I < 15;

j ~ 6 ^ 3 < I < 10,

• ¹    Часть I см. // Имущественные отношения в Российской Федерации. 2004, № 3.

• ²    Виленский П.Л., Лившиц В.Н., Смоляк С.А. Оценка эффективности инвестиционных проектов. Академия народного хозяйства при Правительстве Российской Федерации. М.: Дело, 2002.

где «нижняя планка» (соответственно 5, 3, 4, 8, 6, 3) означает минимальный размер первого лота (транша) инвестиций.

Дочерние предприятия, изучив инвестиционные проекты (1), направили в управление инвестиций ПО свои предложения [ A(i, j) ] относительно их участия в инвестиционной стратегии объединения.

Задача (обычно формулируется ЛПР в форме поручения (распоряжения) или приказа): на основе предложений дочерних предприятий управлению инвестиций подготовить проект решения совета директоров об оптимальных финансовых потоках и структуре потенциальных инвесторов (ПО и ДП) в инвестиционных портфелях объединения для следующих состояний макросреды: а) непредсказуемое; б) условно-стабильное; в) стабильное; г) динамично развивающееся. Вербальная модель сформулированной выше комплексной задачи имеет в своих проекциях на четыре состояния макросреды конкретные локальные постановочные задачи: минисуммную, максиминную, минимаксную и максиминную, рассмотрение которых – предмет содержательного изложения настоящей и последующих частей исследования.

Следующим шагом будет поэтапное решение локальных постановочных задач с помощью алгоритмов Егервари и Гросса и методов имитационного моделирования. Для наглядности, количественные показатели ОИП (объемы инвестиционных потоков, млрд р.) проиллюстрируем с помощью виртуальной «корзины» (рис. 1), а качественные показатели ОИП (структуру потенциальных инвесторов) – на орграфах, матрицах, таблицах и одномерных массивах.

Минисуммная постановка задачи

Способ решения – алгоритм Егервари. Макросреда: непредсказуемая. Функционал ( f ): составить ОИП, минимизирующий общий объем инвестиций ПО ( cost_min ).

В условиях непредсказуемого состояния макросреды, инвестиционный портфель формируется из соображений минимизации общего объема инвестиций ПО, в котором преобладают весьма осторожные планы дочерних предприятий, о чем свидетельствует результат решенной задачи (два инвестиционных потока по 3, один – 5, один – 8 и один – 10 млрд рублей, средний объем которых почти в два раза ниже среднего объема инвестиций, объявленного дочерними предприятиями), изложенной далее.

Максиминная постановка задачи

Способ решения – алгоритм Гросса. Макросреда: условно-стабильная. Функционал ( f ): составить ОИП, при котором самый большой объем инвестиций дочернего предприятия окажется минимально возможным, т. е. минимизировать max[i, p(i)] по всем многовариантным версиям.

Как показывает решение, приведенное далее, во всех многовариантных версиях преобладает почти средний объем объявленных дочерними предприятиями инвестиций (три инвестиционных потока по 8, один – 4 и один – 6 млрд рублей), что характеризует все еще осторожное отношение дочерних предприятий к изменению состояния макросреды.

Минимаксная постановка задачи

Способ решения – алгоритм Гросса. Макросреда: стабильная. Функционал (f): составить ОИП, при котором самый маленький объем инвестиций дочернего предприятия окажется максимально возможным, т. е. максимизировать min[i, p(i)] по всем многовариантным версиям.

Как показывает изложенное далее решение, дочерние предприятия стали более уверенными в макросреде, что подтверждается преобладанием в портфеле инвестиционных потоков, которые превышают средний объем объявленных дочерними предприятиями инвестиций (два инвестиционных потока по 11, один – 12, один – 13 и один – 15 млрд рублей).

Максисуммная постановка задачи

Способ решения – алгоритм Егервари. Макросреда: динамично развивающаяся. Функционал ( f ): составить ОИП, максимизирующий общий объем инвестиций ПО.

Рисунок 1 дает визуальное представление о смещении акцентов в инвестиционной стратегии ПО в зависимости от условий его окружения.

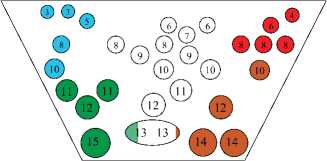
Рис. 1. Виртуальная корзина с ОИП для 4-х состояний макросреды

Обобщенные результаты по всем постановочным задачам будут изложены в последней части исследования.

Минисуммная постановка задачи

Решение

8 s ar

Содержание и иллюстрации в виде одномерных массивов, матриц (таблиц) и графов

<12 11 10 10 14 б<

A(i. j) =

^8 12 10 И 8 6)

, см. Приложение 1

a

Ж s xo

О

Приводим матрицу A(i, j) сначала по строкам, а затем и по столбцам с помощью постоянных приведения (const). Затем строим: а) двудольный граф на основе нулевых решений; б) начальное паросочетание М* «жадным» алгоритмом (паросочетанием в двудольном графе называется множество ребер, не имеющих общих вершин. Изначально паросочетаний может быть несколько. Мы делаем акцент на начальное паросочетание М*. которое имеет заданный алгоритм построения - «жадный»).

\j	Г	2'	3'	4'	5'	б'	О
1	б	5	4	4	8	0	6
2	10		1	5	5	6	3
3	8	5	И	б	12	0	3
4	0	2	7	3	1	5	5
5	2	б	4	5	2	0	6

X	г	2'	3'	4'	5'	6'
1	6	5	3	1	7	0
2	10	0	0	2	4	б
3	8	5	10	3	И	0
4	0	2	6	0	0	5
5	2	б	3	2	1	0
и	0	0	1	3	1	0

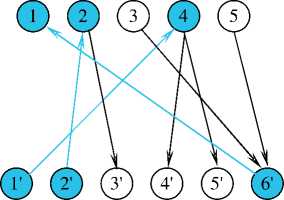
Результат 1 -й итерации: увеличивающейся относительно М* цепи нет, но остаются ненасыщенными вершины 3 и 5, следовательно, наибольшее паросочетание нс построено. Переходим ко 2-й итерации.

Применим к трансформированной матрице, которая имеет наибольшее количество нулей, операцию Егервари Е(Г, Г, d).

Множество вершин, достижимых из 3 и 5:

для 8 = 3 такое множество {6’, 1 }~1     ,        ,     , для 8 = 5 такое множество {б', 1IJ - 11L J - {6 ).

Среди элементов b[i. j], где i е Г, a j е J" = JV находим элемент минимального веса, это Ь[1, 4'] = 1, в приведенной матрице обозначим его выделенным шрифтом (4).

\j	Г	2'	3'	4'	5'	6'
1	6	5	3	1	7	0
2	10				4	6
3	8	5	10	3	И	0
4		2	6			5
5	2	6	3	2	1	0

\j	Г	2'	3'	4’	5'	6'
1	5	4	2		6
2	10			2	4	7
3	8	5	10	3	11
4		2	6			6
5	2	6	3	2	1

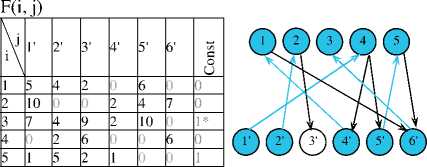
Наибольшее паросочетание получилось сразу из начального паросочетания «жадным» алгоритмом (по коротким матричным ребрам).

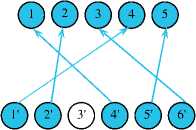
Мы получили оптимальный инвестиционный портфель (I, J) в логистическом решении на основе теории графов в виде одномерного массива Nas_u = {4, 2, 6, 1, 5}. Двумерное отображение решения можно представить не только в виде орграфа G', но и в виде таблицы и/или матрицы B(i, j). Покажем это схематично в последовательности: A(i, j), G'. B(i, j).

	'12	11	10	10	14	6>
	13	3	4	8	8	9
A(i,j) =	11	8	14	9	15	3	—> Nas_u = (4,2,6,1,5)
	5	7	12	8	6	10
	v8	12	10	11	8	6

ВЦ, jj

\j	Г	2'	3’	4*	5'	6'
1				1
2		1
3						1
4	1
5					1

2 2 о

и

О

Если полученные объемы инвестиционных потоков, составляющие оптимальный инвестиционный портфель ПО, обозначить выделенным шрифтом (напр. 1О> в исходной матрице A(i, j), то сумма выделенных элементов окажется равной 29 (10+3+3+5+8). Это и есть значение функционала, соответствующее оптимальному инвестиционному портфелю в исходной задаче для непредсказуемой макросрсды, f = cost_min = 29: Nas_u = {4, 2, 6, 1, 5}.

Максисуммная постановка задачи

Решение

3 3 в* 1	Содержание и иллюстрации в виде одномерных массивов, матриц (таблиц) и графов
ч о СО m	42  И  10 10 14 б' A(i, j) =......  см. Приложение 1 .8  12  10  11  8  6у

Приводим матрицу A(i, j) сначала по строкам, а затем и по столбцам с помощью постоянных приведения (const). Затем строим: а) двудольный граф на основе нулевых решений; б) начальное паросочетание М* «жадным» алгоритмом (по коротким матричным ребрам).

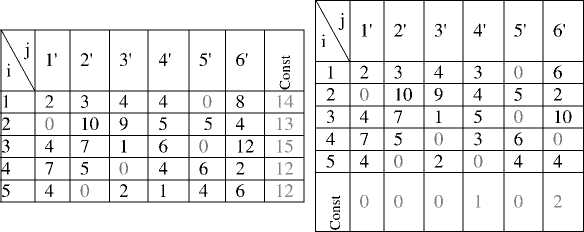
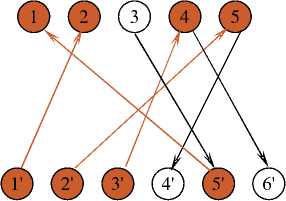
Результат 1-й итерации: увеличивающейся относительно М* цепи нет, но остается ненасыщенной вершина 3, следовательно, наибольшее паросочетание не построено. Переходим ко 2-й итерации.

Применим к трансформированной матрице, которая имеет наибольшее количество нулей, операцию Егервари Е(Г, J', d).

Множество вершин, достижимых из вершины 3. есть {5', 1), следовательно, Г = {1}, Г = {5'}.

Средн элементов b[i. j], где i е Г, a j е J" = JV находим элемент минимального веса, это b[l, 1] = 2. который в таблице обозначим выделенным шрифтом (2).

\j	Г	2'	3'	4'	5'	6'
1	2	3	4	3	0	6
2	0	10	9	4	5	2
3	4	7	1	5	0	10
4	7	5	0	3	6	0
5	4	0	2	0	4	4

Е(Г. г, d)

\ j	Г	2*	3*	4'	5'	6'
1	0	1	2	1	0	4
2	0	10	9	4	7	2
3	4	7	1	5	2	10
4	7	5	0	3	8	0
5	4	0	2	0	6	4

Трансформирование

	Г	2'	3'	4'	5'	6'	и
1	0	1	2	1	0	4
2	0	10	9	4	7	2
3	3	6	0	4	1	9
4	7	5	0	3	8	0
5	4	0	2	0	6	4

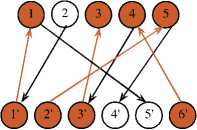
Как видим, наибольшее паросочетание из М* сразу не получилось, однако мы имеем увеличивающуюся относительно М* цепь благодаря наличию чередующейся цепи (2. 1', 1, 5'). Техническое построение наибольшего паросочстания G' получается заменой тонкого ребра (1, 1') на жирное, а жирных ребер (2, Г) и (1,

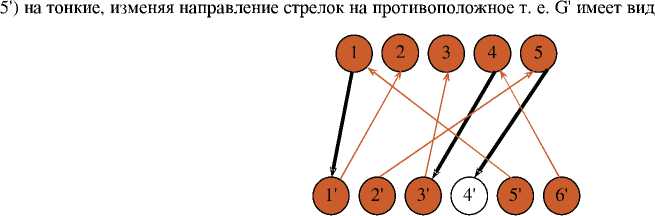
Мы получили оптимальный инвестиционный портфель (1, J) в логистическом решении на основе теории графов в виде одномерного массива Nas_u = {5, 1, 3, 6, 2). Двумерное отображение решения можно представить не только в виде орграфа G', но и в виде таблицы BT[i, j] и/или матрицы BM(i, j), а также совмещенного орграфа GS (рис. 3).

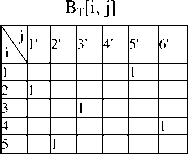
	(°	0	0	0	14	0 )
	13	0	0	0	0	0
вма j) =	0	0	14	0	0	0
	0	0	0	0	0	10
	1 0	12	0	0	0	0 J

Если полученные объемы инвестиционных потоков, составляющие оптимальный инвестиционный портфель ПО, обозначить выделенным шрифтом (напр. 14 в исходной матрице A(i, j), то сумма выделенных элементов окажется равной 63 (14+13+14+10+12). Это и есть значение функционала, соответствующее оптимальному инвестиционному портфелю в исходной задаче для динамично развивающейся макросрсды.

f 12 11 10 10 14 6 13 3 4 8 8 9 =4> Nas_u = {5,1,3,6,2} ^> cost_max = 14 + 13 + 14 + 10 + 12 = 63 A(i,j) = 11 8 14 9 15 3 5 7 12 8 6 10 8 12 10 11 8 6 J f = cost_max = 63, Nas_u ={5,1, 3, 6, 2), Ео = 63.

Орграф G _S

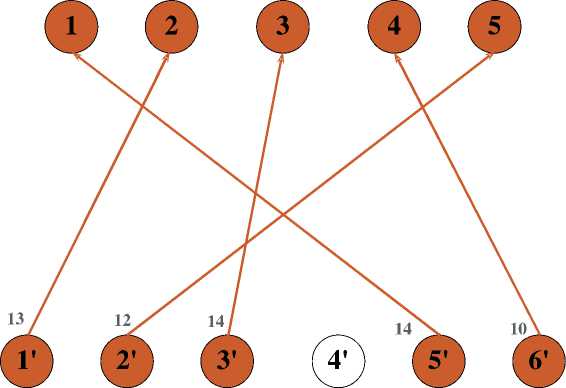
Рис. 3. Орграф, совмещающий матрицу BM(i, j), таблицу BT[i, j] и одномерный массив Nas_u = {5, 1, 3, 6, 2}

Приложение 1

Исходные данные: матрица A(i, j), граф G

где A(i, j) – матрица предпочтений дочерних предприятий;

i = (1:5) - номер (условный) дочернего предприятия (строка матрицы);

j = (1’:6’) - номер (условный) эмитента (столбец матрицы);

a(i, j) – объем заявленных инвестиций i -го дочернего предприятия в j -й вид акций инвестиционного портфеля, вес ребра u(i, j) ;

G – двудольный неориентированный граф, построенный по данным матрицы A(i, j) ;

I – множество дочерних предприятий, I = {1, 2, 3, 4, 5};

J – множество финансовых активов (видов акций), J = {1’,2’,3’,4’,5’,6’};

u(i, j) – ребра, соединяющие множества I и J на основе матрицы A(i, j) ;

f – функционал (критерий);

Nas_u – одномерный массив, инвестирование I в J , Nas_u = {…..};

f = ?, Nas_u = ?

Постановка задач, способы их решения и состояние макросреды в обобщенном виде

^^^^^^^'-^ КПЗ/СР Непредсказуемая (А) Условностабильная (В) Стабильная (С) Динамично развивающаяся (D) Производный эффект Минисуммная _,/-'''алгоритм Егервари 7 ? 7 ? ? Максиминная ^/^/M\VO'^WXW Г росса 7 ? 7 ? ? Минимаксная ^/^^ajxvo^wxw Г росса 7 ? 7 ? ? Максисуммная ^/^^ ^/anvo^wx^ Егервари 7 ? 7 7 ? где КПЗ – категория постановки задачи (минисуммная, максиминная, минимаксная, максисуммная);

СР – способ решения задач (алгоритмы Егервари, Гросса);

A, B, C, D – итоговые суммы оптимального (рационального) инвестиционного портфеля ( A < B < C < D );

? – поиск результатов.

Приложение 2

Математическое описание алгоритма Егервари

s s Ш Q. Ф H S	КАТЕГОРИЯ ПОСТАНОВКИ ЗАДАЧИ
	МИНИСУММНАЯ	МАКСИСУММНАЯ
§ CQ OQ	a[i, j] - массив, задающий заявки дочерних предприятий (млрд р.) на участие в инвестиционных проектах	a[i, j]
§ I s s	dob - рабочая переменная, хранящая сумму коэфф, приведения по строкам и столбцам; cpst_min - минимальная по сумме заявка; rpass_l[i], mass_J[j] - список строк Г и столбцов J'; Nas_u[i, j] - найденное на очередной итерации максимальное паросочетание; NasJ(M) рабочие массивы с элементами Nas_J(N) типа boolean, содержащие информацию о насыщенности вершин из м-в I и J, все элементы изначально равны false (т. е. характеристика неориентированного двудольного графа)	dob - рабочая переменная, хранящая сумму коэфф, приведения по строкам и столбцам; cost_max - максимальная по сумме заявка; mass_l[i], mass_J[j] - список строк Г и столбцов J'; Nas_u[i, j] - найденное на очередной итерации максимальное паросочетание; Nas_l(M) рабочие массивы с элементами Nas_J(N) типа boolean, содержащие информацию о насыщенности вершин из м-в 1 и J, все элементы изначально равны false (т. е. характеристика неориентированного двудольного графа)
>s §э 1	Привести массив a[i, j] в цикле по i = 1+М (по строкам) в цикле по j = 1+N найти мин. эл-т min[i] в цикле по j = 1+N a[i, j): = a[i, j] - min[i] dob: = dob + min[i] в цикле no j = 1+N (по столбцам) в цикле no i = 1+М найти мин. эл-т min[j] в цикле по i = 1+М a[i, j]: = a[i, j] - min[j] dob: = dob + min[j] cost_min: = dob	Привести массив a[i, j] в цикле по i = 1+М (по строкам) в цикле по j = 1+N найти макс, эл-т max[i] в цикле по j = 1+N a[i, j]: = max[i] - a[i, j] dob: = dob + max[i] в цикле no j = 1+N (по столбцам) в цикле no i = 1+М найти мин. эл-т min[j] в цикле по i = 1+М a[i, j]: = a[i, j] - min[j] dob: = dob + min[j] cost_min: = dob
2	Использовать Алгоритм построения максимального паросочетания, ввод: a[i, j], вывод Nas_u[i], u[i, j]	Использовать Алгоритм построения максимального паросочетания, ввод: a[i, j], вывод Nas u[i], u[i, j]
3 3.1 3.2 3.3 3.4	Выбрать ненасыщенные вершины и сформировать множества Г и J' В цикле по i = 1+М, если Nas_l[i] = false (т. е. ненасыщенная вершина), то использовать Алгоритм нахождения вершин, достижимых из данной: ввод Nas_l[i], u[i, j]; вывод: Pi[k] На основе всех Pi[k] сформировать р[к] - указать в нем номера вершин таких, что Pi[k] = -1 хотя бы для какого-нибудь i Среди элементов b[i, j], где: i е Г, j g J" = J\J' определить min В цикле по i = 1+М и i g Г, по j = 1+N и j g J1, b[i, j]: = b[i, j] - min, когда i g Г и b[i, j]: = b[i, j] + min, когда j g J' Возврат к n. 2	Выбрать ненасыщенные вершины и сформировать множества Г и J' В цикле по i = 1+М, если Nas_l[i] = false (т. е. ненасыщенная вершина), то использовать Алгоритм нахождения вершин, достижимых из данной: ввод Nas_l[i], u[i, j]; вывод: Pi[k] На основе всех Pi[k] сформировать р[к] - указать в нем номера вершин таких, что Pi[k] = -1 хотя бы для какого-нибудь i Среди элементов b[i, j], где: i е Г, j g J"=J\J' определить min В цикле по i = 1+М и i g Г, по j = 1+N и j e J1, b[i, j]: = b[i, j] - min, когда i g Г и b[i, j]: = b[i, j] + min, когда j g J' Возврат к n. 2
CQ	Nas_u[i] - массив, задающий вариант оптимального инвестиционного портфеля cost_min - суммарный объем инвестиций ПО

Приложение 3

Комментарий к математическому описанию алгоритма Егервари

Формулировка задач в терминах теории графов : дочерним предприятиям i (i = 1M) и инвестиционным проектам j (j = 1N) ставятся в соответствие вершины графа, а возможность участия i -го дочернего предприятия в j -м инвестиционном проекте отображается наличием в графе ребра u(i, j) с весом a(i, j) .

Возможные типы задач:

• •    максисуммная постановка. Даны M дочерних предприятий объединения и N инвестиционных проектов, отобранных экспертами и финансистами ПО , для формирования оптимального инвестиционного портфеля в условиях изменяемых состояний макросреды. Составить инвестиционный портфель, максимизирующий общий объем инвестиций ПО .

• •    минисуммная постановка. Составить инвестиционный портфель, минимизирующий общий объем инвестиций объединения.

Постановка задачи.

Дан двудольный граф G = с взвешенными ребрами и матрицей весов A(i, j) . Найти наибольшее паросочетание M * такое, что сумма a(i, j) по ребрам u(i, j) , принадлежащим M *, будет минимальна (максимальна).

Основная идея.

Суть алгоритма в том, чтобы привести матрицу по строкам и столбцам к виду с наибольшим числом нулей, т. е. b(i, j) = 0. Строится двудольный граф, где ребра соответствуют нулям. Затем по начальному паросочетанию, построенному «жадным» алгоритмом (по коротким ребрам), используя метод чередующихся целей, находится большее паросочета-ние. Если оно (большее паросочетание) оставляет некоторые вершины множества I ненасыщенными, то его следует увеличить. Для этого матрица вновь преобразовывается в целях повторной попытки построить наибольшее паросочетание. И так до тех пор, пока все вершины множества I не станут насыщенными.

Возможные сложности.

Как преобразовать матрицу, чтобы стало возможным увеличение полученного (начального) паросочетания?

Способы преодоления.

К приведенной матрице применяется так называемая операция Егервари E(I’, J’, d) : из каждой строки i из множества I ’ вычитается d , а к каждому столбцу j из множества J ’ прибавляется d , причем I ’ ⊂ I , а J ’ ⊂ J . Множества I ’ и J ’ определяются с помощью ненасыщенных вершин (стрелки ребер, исходящих из ненасыщенных вершин ориентированного двудольного графа, указывают на множества I ’ и J ’). Число d = b(i, j) – это элемент минимального веса среди элементов b(i, j) , где i ∈ I’ , j ∈ J ’’ = J\J ’. После проведения операции Егер-вари E(I’, J’, d) , станет возможным повторное приведение матрицы по строкам и/или столбцам, а полученное на основе такой матрицы начальное паросочетание окажется больше предыдущего.

Описанный алгоритм основан на идеях работы венгра Егервари, написанной еще в 1931 году.

Продолжение следует