Комплексный подход к оценке прочности сварных тавровых соединений

Повышение эффективности работы тавровых сварных соединений можно достичь путем выбора оптимальных сечений сварных швов, характеризующихся наименьшим количеством наплавленного металла при заданных нагрузках. Очевидно, что проектирование сварных соединений с неполными проплавлениями и пониженными сечениями угловых швов должно быть основано на соответствующих расчетных методиках оценки их прочности. Существующие методики расчета на прочность тавровых соединений с угловыми швами разработаны в основном для равнокатетных швов, то есть для частного случая их геометрической формы. Последнее значительно ограничивает использование предлагаемых расчетных методик и не позволяет провести оптимизацию геометрических параметров рассматриваемых соединений с точки зрения обеспечения их максимальной несущей способности при заданном объеме наплавленного металла. В данной работе приведены комбинированные расчетные методики оценки несущей способности угловых швов в условиях вязкого разрушения и их сопротивляемости квазихрупким и хрупким разрушениям с учетом локальных пластических деформаций в окрестности места сопряжения и величины радиуса последнего.

Теоретический анализ вязкой прочности тавровых соединений был выполнен с использованием кинематической теоремы предельного равновесия [1]. При этом приняты следующие упрощающие условия и допущения: металл соединений изотропный, однородный и идеально упругопластический, подчиняющийся условию текучести Губера-Мизеса. На основе экспериментальных данных была принята следующая расчетная схема, отражающая характер пластического деформиро вания и особенности напряженного состояния тавровых соединений с угловыми швами (рис. 1). В предельном состоянии, характеризующем вязкое разрушение рассматриваемых соединений, очаг пластической деформации может быть представлен упрощенными линиями скольжения ОД, совпадающими с плоскостью вязкого разрушения.

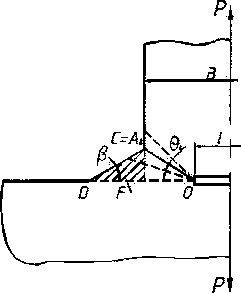
Рис. 1. Тавровое соединение с диапазоном изменения угла 0;

Согласно [1] мощность внутренних w_L и внешних w_p сил на единицу длины соединения в плоскости, перпендикулярной чертежу (рис. 1), определяется выражениями:

wL=2.kULlp; wp=PU0, (1) где к - предел текучести материала при чистом сдвиге, к = <зТ]4з - для неупрочняющихся материалов, к = ов /л/з - для упрочняющихся в процессе пластического деформирования материалов [1], (стт и ов - соответственно предел текуче- сти и прочности материала); 1р - размер поверх ности разрушения ОА, в плоскости чертежа,

9,-arJS]; 4™-^.   (5)

(nJ Vtgp

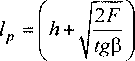
sinp sin(p + 0,)

; h - глубина проплав

ления; р - угол наклона образующей шва; F —

площадь шва; Р - погонное предельное усилие; U_L - скорость перемещения материальных частиц при пластическом течении вдоль линий скольжения ОА,, U_L = U₀/sm9j , U_o - средняя скорость деформирования.

Исходя из баланса мощности внутренних и внешних сил (w_L = w_p ) получено выражение для

В третьем диапазоне (р„ > Р > 0 ) траектория непровара распространяется от вершины непровара стенки тавра О до вертикальной (боковой) ее поверхности (штриховая линия на рис. 1). Угловой шов в этом случае не вступает в пластическую деформацию:

оценки несущей способности (средних предельных напряжений аср) рассматриваемых сварных соединений;

В 2      ,

CTcp=- = ^|^V^p,

где iy - V2F /в — относительная площадь наплав

ленного металла (В - толщина пластины); к^ - коэффициент, зависящий от геометрических параметров сварных соединений. В общем виде коэффициент может быть представлен в следующем виде:

, fl) sinp

= Т] + —р=-- у- ----7-----,        (3)

Р ( VtgPj sm(p + 0,)sm0,

9,-2; 4g -2Л. (6)

Анализ полученных выражений (2)-(6) открывает возможность оптимизировать геометрические параметры угловых швов при конструктивнотехнологическом проектировании рассматриваемых сварных соединений. Из условия 5а_ср/5р = О были найдены соотношения, позволяющие по известной глубине проплавления h и площади наплавленного металла F (т. е. по известному значению параметра г| = h/-J2F ) определить оптимальные углы наклона образующей шва Р = Р_опт, обеспечивающие максимальную способность рассматриваемых сварных соединений:

_ 1 2cosP_onT V2sin-2p_onT

где x\ = hjA2F - относительная глубина проплав

ления пластин.

Угол наклона плоскости вязкого разрушения 9, находим из условия минимума мощностей (dw_L dw_P )

—— = —— = 0 . В зависимости от сочетания (59,    59,     )

геометрических параметров тавровых соединений имеют место три диапазона изменения угла 9, характеризующихся местоположением точки А, по отношению к вершине углового шва С (рис. 1).

В первом диапазоне (л/2>р>р*, где Р* -граничные значения углов р, определяемые из

Рис. 2. Зависимость оптимальных значений углов Ропт от относительной глубины проплавления Т] таврового соединения (I, II, III - диапазоны изменения углов Р)

уравнения р = tg—

^/tgP* ) траектория вязкого раз

рушения, совпадающая с линией скольжения ОА,,

распространяется от вершины непровара стенки тавра О до наклонной поверхности углового шва CD (штриховая линия на рис. 1):

Во втором диапазоне (Р* > Р > р** = arctg ц2)

траектория вязкого разрушения распространяется от вершины непровара стенки тавра О до точки перехода углового шва к основному металлу А₂ = С (рис. 1 ):

Зависимости оптимальных значений углов ропт от относительной глубины проплавления г] приведены на рис. 2. Как следует из выражения (7), для тавровых соединений, выполненных ручной дуговой сваркой без проплавления стенки, оптимальное значение угла Ропт = 60° . С увеличением относительной глубины проплавления ц тавровых соединений оптимальные значения углов наклона образующей швов ропт смещаются в область больших величин (ропт > 60°). Следует отметить,

что оптимальные значения углов Ропт находятся в I диапазоне их изменения.

Оценку несущей способности рассматриваемого сварного соединения в условиях квазихруп-кого и хрупкого разрушения осуществляли, используя критерий обобщенного нормального разрыва [2], в следующей форме:

<^кр = р— > (8)

VN2 -ф^ф^фр где К1с - критическое значение коэффициента интенсивности, при котором произойдет разрушение; фк - поправочная функция; учитывающая конечность геометрических размеров; фх - поправочная функция, учитывающая совместное действие нормальных и сдвигающих напряжений в окрестности места сопряжения; фщ, - поправочная функция, учитывающая образование зон локальной текучести в окрестностях места сопряжения; Фр - поправочная функция, учитывающая конечность радиуса сопряжения.

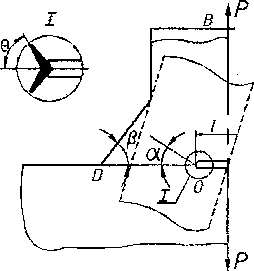
Рис. 3. Расчетная схема таврового соединения с эквивалентной ей пластиной с наклонным трещиноподобным концентратом

Для определения поправочной функции фк рассматриваемое сварное соединение приводили к эквивалентной (с точки зрения идентичности на пряженного состояния и характера локального разрушения в окрестности места сопряжения) пластине с наклонным трещиностойким концентратором напряжений. В результате теоретического анализа было получено следующее выражение:

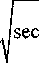
Г Я / 1

(2 ДФ,

Фк

Ф,Ф2

где Фь Ф2 - параметрические функции, Ф] = 1 + 2\p^/tgp • tgy*, Ф2 = sin2 у*, у* - угол наклона трещиноподобного концентратора в эквивалентной пластине (рис. 3).

В условиях нагружения смешанного типа напряженное состояние в окрестности вершины концентратора определяется коэффициентами интенсивности напряжений Кх и Кй, отношение которых Х = K-JКп согласно [2] описывается выраже нием X = ctgy*.

Согласно работе [3], параметр X определяет направление страгивания трещины от места сопряжения (угол и^):

since, 3cosa, -1

Для определения поправочной функции фх получено следующее выражение:

cos(a/2) Фх = , У 1 + А."

(И)

Функция фга, учитывающая локальную текучесть в окрестности вершины концентратора, с учетом особенностей, вносимых смешанным типом нагружения равна: .

А 41 А2+2,06

Фпл =”-----------

тавровых значение

Фх реальных геометрических параметров соединений (Р = 30...70°, р = 0...1,2)

X находится в пределах 0...0,2, следова- тельно, поправочная функция фх практически равна единице (фх= 1,0... 1,015), а поправочная функция фпл= 1,4.

Дефекты типа непровара в тавровых соединениях имеют больший радиус в вершине, чем усталостная трещина. Оценивать несущую способность таких соединений следует с учетом радиуса в вершине непровара. Локальные разрушения соединения согласно [3] происходят при условии достижения коэффициентом интенсивности напряжений значения К_Хс^ = К_Хс p_Q/р , где К_1с(р) -критический коэффициент интенсивности напряжений с учетом радиуса концентратора р, р₀ -эффективное значение радиуса концентратора.

Значение р0 может быть приближенно определено по механическим свойствам материала [4]:

0,08( ^ро=— — 2тг I О-

Поправочная функция фр имеет вид:

ФР =Vpo/P •

Используя приведенные соотношения для оценки поправочных функций фк , фх, Фщ,, Фр , можно определить несущую способность сварных соединений с угловыми швами в условиях хрупкого (квазихрупкого) разрушения по известным конструктивно-геометрическим параметрам р, р, ф и р тавровых сварных соединений.

Расчет предельного состояния при квазихруп-ком разрушении сварных тавровых соединений с неполным проплавлением можно провести, используя комбинированный критерий, предложенный Е.М. Морозовым для соединений с предусмотренными трещиноподобными несплошностями [5, 6].

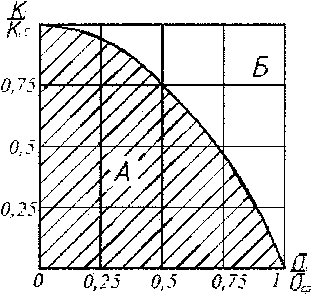
Рис. 4. Диаграмма предельного состояния таврового сварного соединения

Для сварных тавровых соединений, склонных разрушаться как вязко, так и хрупко, оценка предельного сопротивления разрушению может быть получена по зависимости

— 1 =1, (15)

где ст - напряжение, приложенное к сварному соединению при вязком разрушении, стср - проч ность сварного соединения при вязком разрушении, Ку - коэффициент интенсивности напряжений, KY = ga/tU ■ ФкФхФплФр, К1с — критический коэффициент интенсивности напряжений, при котором реализуется хрупкое разрушение А)с =СТкр^Чркф;фп/рр.

На рис. 4 приведена диаграмма предельного состояния при квазихрупком разрушении таврового сварного соединения согласно формуле (15). В области А расположено безопасное сочетание нагрузок для данного сварного соединения, в области Б произойдет квазихрупкое разрушение.

Предложенная методика расчета оценки прочности тавровых сварных соединений с непроваром в корне шва позволяет осуществить выбор оптимальных геометрических параметров сварных швов (угол наклона катета шва, глубина проплавления и т. д.) таким образом, чтобы с учетом действующих нагрузок по комбинированному критерию данное соединение не попало в область ква-зихрупких разрушений.