Комплексный подход к решению задачи структурного синтеза мультипроцессорных устройств обработки сигналов мобильных инфокоммуникационных систем

Высокий уровень «интеллекта» современных систем и сетей мобильной связи является следствием успешной конвергенции телекоммуникационных и информационных технологий и объединения широкого спектра возможностей по высокоскоростной транспортировке динамичных и неравномерных объемов информации с заданной степенью достоверности по различным каналам связи на фоне комплекса разнообразных помех.

Можно выделить несколько основных аспектов, характеризующих особенности функционирования, предоставляемые услуги и системотехнический уровень современных и перспективных мобильных систем связи, неизбежно выделяющихся в отдельный класс систем передачи и обработки информации – мультисервисные мобильные инфокоммуникационные системы (ММИС) – и проанализировать принципиальные моменты, определяющие стратегию их разработки и продвижения на современный телекоммуникационный рынок.

• 1.    Мобильные инфокоммуникационные системы всего за последние два десятилетия прошли колоссальные по наукоемкости и технологичности этапы своего развития: от систем первого поколения (1G) до систем 4-го поколения (4G) с четко намеченной перспективой их дальнейшего развития. В настоящее время для передачи интегрального пакетного трафика широко используются различные технологии сетевых радиослужб: GPRS, EDGE, EVDO, WCDMA, HSDPA, WLAN, WiMAX, LTE, предоставляющие пользователю широкий спектр услуг с удовлетворительными скоростями передачи данных, а также гибкие возможности поддержки различных профилей качества обслуживания (QoS) как на уровне радиоинтерфейса, так и на уровне базовой сети.

• 2.    Программное обеспечение и аппаратная поддержка современных сетевых элементов мобильных сетей позволяют строить на их основе полнофункциональные масштабируемые сетевые инфраструктуры, обеспечивающие баланс сетевой нагрузки при заданном уровне надежности работы сети и предоставлением сквозного транспортного сервиса.

• 3.    Мощный теоретический фундамент статистической радиотехники и оптимального приема сигналов открыли для практической реализации целое научное направление в обработке сложных сигналов в негауссовских каналах, опирающееся на новый класс математических моделей, методов и алгоритмов посткорреляционного уровня, поддерживаемых протокольными стеками радиоинтерфейсов ММИС новых поколений с обеспечением функциональности заданного качества обслуживания внутрисетевого интегрального трафика.

• 4.    Заметный технологический прорыв в процессорной технике, ПЛИС и функциональной микроэлектронике снимает сегодня существенные ограничения вычислительной сложности реализуемых алгоритмов, обеспечивая компактные программно-аппаратные решения, реализующие высокоэффективные устройства обработки сигналов как для базовых станций, так и для мобильных терминалов.

Эти обстоятельства позволяют сегодня пересматривать и оптимизировать стратегию проек- тирования устройств ММИС с целью получения наиболее эффективных и рентабельных с точки зрения «качество работы – вычислительная сложность» алгоритмических и аппаратно-программных решений, повышающих комплексную эффективность работы сети и использования сетевых ресурсов.

Методика совместного анализа, синтеза иоптимизациипостроенияпрограммно-аппаратных средств ММИС

Анализ современных тенденций и перспективных направлений развития алгоритмического и аппаратного обеспечения приемников ММИС показывает, что основные усилия разработчиков и исследователей связаны с поиском проблемноориентированных квазиоптимальных алгоритмических решений, адекватных, с одной стороны, используемым математическим моделям и методам, а с другой – последующей вычислительной реализации. При этом четко видна тенденция к получению параллельных вычислительных архитектур устройств совместной обработки сигналов пользователей, эффективно реализующихся на базе высокоскоростных ПЛИС, обеспечивающих потоковую обработку векторно-матричных операций.

При этом на уровне физического радиоинтерфейса и канальном уровне соответствующими алгоритмами не в достаточной мере используется вся доступная информация об информационном взаимодействии в установленном соединении, параметрах принимаемых сигналов и помеховой обстановки для более рационального задействования внутрисетевых ресурсов, в частности, правил доступа в единый радиоканал, вида модуляции и кодирования, чиповой скорости передачи, размерности протокольных блоков, синхронизации, вероятностно-временных характеристик прямого и обратного каналов, классифицируемых параметров QoS и др.

Это требует введения дополнительных организационно-технических мер по высокоскоростной и надежной передаче в сети интегрального пакетного трафика (характеризующегося неста-ционарностью, неоднородностью, долговременными пульсациями, мультифрактальностью) в сложных и изменчивых условиях информационного взаимодействия в радиоинтерфейсах сетей радиодоступа ММИС. Интенсивная эксплуатация средств мобильных инфокоммуникацион-ных систем со свободным доступом абонентов в единый радиоканал неизбежно сопровождается постоянно растущими требованиями к вероят- ностно-временным характеристикам информационного обмена и эффективности использования радиочастотного спектра.

Внедрение специализированных мультипроцессорных программно-аппаратных средств, построенных на базе сигнальных процессоров, ПЛИС-технологии и элементов функциональной микроэлектроники, представляет собой сложнейшую комплексную задачу системного плана, которая требует решения разнообразных вопросов, связанных с разработкой специальных алгоритмов обработки сигналов, выбором архитектурных решений и программного обеспечения таких систем при определенных ограничениях на аппаратно-программные и сетевые ресурсы.

Ведущую роль при этом занимает вопрос о согласовании и оптимизации архитектуры программно-аппаратных средств системы связи с реализуемыми алгоритмами, который заключается в совместном формализованном синтезе как структур алгоритмов, так и структур мультипроцессоров. Речь идет о создании проблемно-ориентированных систем, для которых в [1-2] определен системный подход в виде «отображения проблем вычислительной математики на архитектуру вычислительных систем». Это означает, что чем выше быстродействие мультипроцессорной структуры, достигаемое за счет архитектурных решений, тем уже класс алгоритмов, эффективно реализующихся на ней.

Другими словами, структуры параллельных алгоритмов тесно связаны со структурой параллельных вычислительных систем и поэтому нецелесообразно рассматривать их изолированно. Чтобы в полной мере реализовать преимущества параллельной организации вычислений, следует добиваться соответствия топологической структуры мультипроцессорной системы структуре алгоритма. Общность методов и средств организации параллельной обработки данных связывается с представлением параллельных алгоритмов в виде, отражающем, в первую очередь, внутренний параллелизм задачи. Все это приводит к необходимости решения проблемы по созданию специализированных мультипроцессорных структур, архитектурно адекватных реализуемым алгоритмам, что, в свою очередь, связано с разработкой средств формального совместного описания структур алгоритмов и структур систем.

Недостаточное развитие альтернативных методик совместного исследования вероятностных моделей СПО, алгоритмов обработки радиосигналов, вычислительных методов и архитектур параллельных вычислительных средств обуслав- ливает актуальность разработки новых классов моделей и методов синтеза, анализа и оптимизации специализированных мультипроцессорных систем обработки сигналов, адекватных полученным алгоритмам обработки наблюдаемых случайных сигналов (процессов). Решение этой проблемы базируется также на разработке методов математического моделирования процедур многоуровневого структурного и логического синтеза с использованием проблемно-ориентированных баз знаний и соответствующих подсистем функционального проектирования в рамках интегрированных САПР.

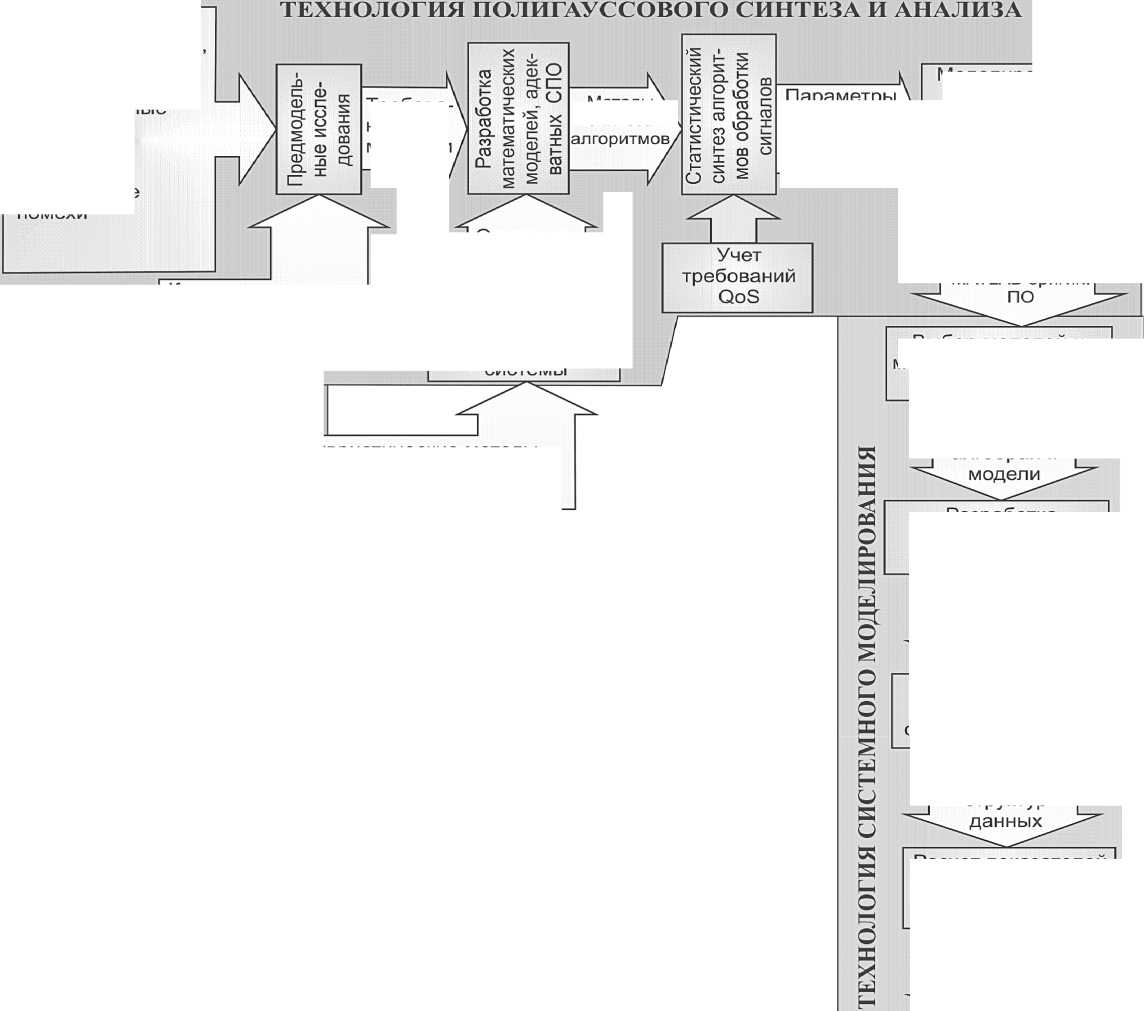
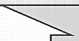
На рис. 1 представлен комплексный системный подход, объединяющий в единый процесс исследования комплекс взаимосвязанных частных задач, эффективное решение которых становится возможным благодаря корректному и целенаправленному использованию посткорреляционных математических моделей на основе смесей вероятностных распределений, синтезу соответствующих эффективных алгоритмов и программно-аппаратных мультипроцессорных средств обработки сигналов в негауссовских каналах, а также разработке и использованию процедур оптимизации и сквозного управления качеством обслуживания (QoS) интегрального внутрисетевого трафика [3].

В настоящее время для разработки проблемно-ориентированных алгоритмов и устройств обработки сигналов используются различные модели и методы адекватного описания сигнально-помеховой обстановки в каналах ММИС, различные модели и методы формализации процедур структурного синтеза мультипроцессорных структур с различной степенью параллелизма, а также различные модели и методы физического полунатурного моделирования, обеспечивающие первичную «обкатку» синтезированных алгоритмов на базе ПЛИС для получения оценок эффективности их работы при выбранном критерии качества. В этой связи в представленном на рис.1 комплексном подходе совместного моделирования, анализа и структурного синтеза программно-аппаратных средств, реализующих исходные алгоритмы с заданным уровнем эффективности, выделяются четыре основные технологические плоскости:

• -    технология полигауссового синтеза и анализа алгоритмов и устройств;

• -    технология системного моделирования;

• -    технология физического моделирования;

• -    технология проектирования и программирования мультипроцессорных устройств обработки сигналов.

Первая плоскость комплексного подхода, по сути, определяет оптимальную стратегию получения конечных решений, т.к. отражает выбор и разработку математических моделей, адекватных поставленной задаче полного вероятностного описания сигнально-помеховой обстановки в каналах ММИС и синтеза оптимальных и ква-зиоптимальных алгоритмов обработки широкополосных сигналов. В рамках данной статьи рассмотрим суть проблем, решаемых в этой плоскости более подробно.

Важным для предметной области статистической теории систем связи является то, что эффективность работы синтезируемых алгоритмов предопределяется используемыми математическими моделями сигналов, помех и устройств. Однако в большинстве случаев выбор вероятностных моделей описания сигнально-помеховой обстановки (СПО) проводится, как правило, без объективного учета структуры и элементной базы устройств, реализующих алгоритмы обработки сигналов. Тогда как из счетного множества возможных разнообразных формальных моделей, отражающих СПО с требуемой точностью, следует выбирать подмножества, в определенном смысле адекватные последующим вычислениям и средствам их реализации. Причем выбор подмножеств должен осуществляться вне субъективизма разработчика, исходя из требований к математическим моделям и определенным их параметрам, что позволяет более качественно реализовать комплексный подход к решению задачи синтеза алгоритмов обработки и программно-аппаратных средств.

Представленный подход достаточно оригинален, т.к. преследует цель увязать в единый законченный цикл сквозного проектирования совокупность автономно существующих этапов проектирования любых устройств обработки сигналов. Исходя из изложенной концепции формализованного проектирования алгоритмов и мультипроцессорных устройств ММИС, можно сформулировать две задачи синтеза программноаппаратных средств.

Первая задача – задача синтеза структуры специализированного процессора на основе структур алгоритмов, предопределенных исходной вероятностной моделью. Вторая – связана с выбором вероятностных моделей исходя из предъявленной заранее известной структуры процессора обработки. При этом синтезирован-

Конструирование, технологии и производ ственные факторы

Графовые, сетевые, алгебраич.

Модели систем, структур

Формальное описание алгоритма условия, данные, ограничения.

Выбор моделей и методов структурного моделирования

Методы оптимизации, качественные методы, MATLAB оригин.

Синтез блок-схем процессоров обработки сигналов

Разработка алгоритмической модели

Расчет показателей эффективности мульти-процессора

Динамическое программирование

Выбор численных методов программирования и разработка параллельных программ

Эвристические методы, структурно-подобные, теория систем

СПО:

Полезные сигналы, Внутрисистемные помехи, Межсистемные помехи, Замирания, Шум, Импульсные помехи

Методы параллельного программирования

Технологические процессы

Технология производства аппаратуры на СБИС

Проектирование СБИС процессоров и устройств ФЭ

Прогнозная оценка надежности СБИС процессора

Анализ и оптимизация интегрального трафика

Методы автоматизированного проектирова

Корректировка параметров функционала QoS

Требования к моделям

методы синтеза

Моделирование работы алгоритмов и оценка их эффективности

Проверка адекватности модели проектируемой системы

Выбор элементной базы

Определение степени паралле-

Симулятор временного и поведенческого моделиров ания ПЛИС

Средства прошивки кристалла ПЛИС

Перенос элементов модели MATLAB в синтезируемый код ПЛИС

ТЕХНОЛОГИЯ ФИЗИЧЕСКОГО МОДЕЛИРОВАНИЯ

Интегрированная _______ среда разработки приложений для

ПЛИС

Предпроектная оценка характеристик вычисл. процесса Подсистема интегрированной

САПР

Функциональнологическое проектирование ПЛИС

Рис. 1. Комплексный подход к совместному исследованию, синтезу, анализу и оптимизации вероятностных моделей, алгоритмов обработки сигналов и реализующих их программно-аппаратных средств ММИС ный алгоритм как некоторая детерминированная последовательность действий, ограничивающая максимально возможный параллелизм задачи своими внутренними причинно-следственными связями, обладает, по крайней мере, двумя основными свойствами:

• -    отражает причинно-следственные связи, которые обусловлены исходным вероятностным описанием СПО;

• -    определяет дополнительные причинноследственные связи, отражающие структуру системы, на которую алгоритм ориентирован.

Рассмотрим основные свойства и преимущества нового класса посткорреляционных математических моделей, основанных на смесях вероятностных распределений, являющихся адекватными широкому спектру задач статистической теории оптимального приема сигналов в негауссовской постановке.

Вероятностные смеси: полигауссовы модели адекватного представления случайных сигналов и помех

Для рассматриваемого класса ММИС, базирующихся на технологии кодового разделения каналов, адекватное представление СПО в динамически изменяющейся среде мобильной связи определяется объективной сложностью реальных каналов с переменными параметрами, многолучевостью и замираниями радиосигналов, проблемой «ближней-дальней» зоны, неустойчивостью и многообразием вероятностных распределений параметров СПО, характером и интенсивностью трафика, асинхронностью и случайностью доступа в единый канал многочисленных прие-мо-передатчиков, нарушением ортогональности ансамбля используемых сигнатур, воздействием комплекса внутрисистемных помех, хаотических импульсных помех, сосредоточенных по спектру помех, флуктуационных шумовых, индустриальных помех и пр. Это феноменологически приводит к негауссовским сигнально-помеховым ситуациям в радиоканалах таких систем и, как следствие, к необходимости эффективной работы ММИС в негауссовских каналах.

Указанные обстоятельства в значительной степени ограничивают потенциально достижимые характеристики помехоустойчивости и пропускной способности ММИС в реальной СПО и приводят к необходимости поиска новых системотехнических, алгоритмических, статистических и технологических решений, обеспечивающих гарантированное качество обслуживания (QoS-Quality of Service) со стороны оператора сети при известных ограничениях на пространственные, энергетические и частотно-временные ресурсы.

Для таких задач ограничение только классом стандартных нормальных распределений существенно сдерживает развитие алгоритмического обеспечения современных радиотехнических систем. Условия работы систем связи и структура сигнально-помехового комплекса требуют сегодня более эффективных алгоритмов обработки сигналов, основанных на более полном, чем корреляционный, описании реальных сигналов и помех. Поэтому в настоя- щее время достаточно активно ведутся работы по исследованию и разработке новых классов вероятностных моделей адекватного представления негауссовских случайных процессов и соответствующих методов анализа и синтеза оптимальных и квазиоптимальных алгоритмов обработки сигналов [4-5].

Принципиально новую основу посткорреляционного этапа статистической теории связи и эффективный инструментарий для работы с негауссовскими случайными процессами закладывают научные и практические результаты, полученные творческим коллективом в рамках казанской научной школы при разработке теории смешанных полигауссовых случайных явлений [6].

Благодаря известным достоинствам гауссовских распределений для статистической теории радиоприема при произвольных флуктуациях сигналов и возмущающих воздействий наиболее удобными оказываются смеси именно гауссовских распределений – так называемые полигауссовы модели [6-10], позволяющие описать распределение любых физически реализуемых сигналов с заданной точностью смесью конечного числа гауссовых компонент. Вероятностные смеси гауссовских распределений обладают рядом замечательных свойств, среди которых можно выделить следующие:

• -    вероятностные смеси гауссовских распределений обеспечивают адекватное описание широкого класса нестандартных случайных явлений и позволяют с заданной точностью представлять произвольные, в том числе многомодальные распределения;

• -    класс полигауссовых вероятностных моделей является замкнутым относительно линейных преобразований;

• -    произвольные нестандартные случайные явления описываются с помощью конечного набора параметров, допускающих возможность их статистического оценивания в условиях априорной неопределенности;

• -    использование полигауссового подхода позволяет использовать весь огромный теоретический и практический потенциал, наработанный в рамках корреляционной теории и ее приложений;

• -    полигауссовы модели и методы обеспечивают аналитическое решение задач синтеза основных классов алгоритмов обработки сигналов и принятия решений в негауссовской постановке;

• -    полигауссовы методы приводят к многоканальным параллельным алгоритмам, в каждом из

каналов которых выполняется однотипный набор стандартных операций не выше второго порядка;

• -    структура получаемых алгоритмов является инвариантной к виду распределений входной информации.

Условия существования полигауссовых моделей любых физически реализуемых процессов обусловливают достаточность описания этих процессов конечным или счетным множеством моментных функций. По определению выборочное пространство {jvj полигауссового процесса содержит выборочные пространства {vV }л всех N компонент и, следовательно, его вероятностная мера //[Л есть взвешенная линейная комбинация гауссовских вероятностных мер лИ, различающихся своими средними или (и) ковариациями [6-7]:

M-^L/'M-IXA'W;

^9„ = 1, п = 1,7V, N < оо,

которые образуют результирующую смесь со своими вероятностями Чп .

Многомерные пл отности вероятности отсчетов U = {г/ Д, к = \,К негауссовского случайного процесса при этом имеют вид

^^x^K^JHII}. (2)

Заметим, что смесь N гауссовских плотностей вероятности, каждая из которых имеет лишь два параметра (среднее и ковариация), в целом обладает числом a_n =3^-l степеней свободы, что обеспечивает существенно большие, чем у одной гауссовской плотности, аппроксимационные возможности: 1 < TV < со. Этим полигауссовы модели, объединяя достоинства вероятностных смесей и моногауссовских моделей, открывают широкие возможности использования результатов корреляционной теории в негауссовских задачах.

Обращаясь к феноменологическому обоснованию, отметим, что выборочные пространства процессов на входе приемника – суть теоретико-множественные объединения случайных комбинаций множеств реализаций флуктуирующих сигналов и продуктов их интерференции. Каждому из этих множеств соответствует своя вероятность присутствия его элемента на входе приемника, а также условная вероятностная мера. Поэтому входному случайному процессу приемника соответствует взвешенная линейная комбинация разных вероятностных мер, т.е. их вероятностная смесь.

Теоретико-вероятностные предпосылки использования именно полигауссовых моделей следуют, в частности, из линейной независимости гауссовских вероятностных мер, различающихся средними или (и) ковариациями. Если множество средних у гауссовских характеристических функций достаточно плотно, то их счетная система может составить неортогональный базис в пространстве £2 комплекснозначных функций, интегрируемых с квадратом модуля на всей вещественной оси [6-8]. При корректном применении формул обращения это приводит к возможности полигауссового разложения функций распределения вероятности. Достаточные условия аппроксимации плотностей вероятности w(z7) конечной гауссовской смесью:

w(0)-^qnN\n, тп

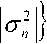
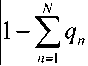
< Е, N < 00

с заранее заданной сколь угодно малой погрешностью £ приведены в [7-8].

Необходимо отметить, что даже при детерминированных моделях составляющих сигнальнопомехового комплекса достаточно негауссовости всего лишь одного из сигналов, чтобы возникла необходимость использования инструментария полигауссового синтеза. Полигауссовы модели случайных явлений образуют широкое множество специфических подклассов, различающихся как свойствами входящих в соответствующие смеси гауссовых компонент, так и свойствами смешивающих вероятностных распределений – «механизмами» смешивания гауссовых компонент. В частности, весьма продуктивными в статистической теории радиосистем являются так называемые «марково-смешанные полигауссовы модели» многоэлементных дискретных сигналов [11].

Для рассматриваемого класса ММИС на уровне физического радиоинтерфейса выполняется обработка достаточно сложных сигнальных конструкций с внутренней взаимосвязью элементов, представляющих собой в общем случае последовательности дискретных многоэлементных сигналов S^{_Sj{t\j^\, каждый из которых представляет собой совокупность K элементарных импульсов

к

8ДО = У/,1к(^к\        (4)

расположенных на временных позициях с коор-динатами t_k, ^g[o, 7], k = \,K; i = M – число типов элементарных сигналов, J – число сигналов в ансамбле, заданных смешанными полигаус-совыми вероятностными моделями. Параметры многоэлементного сигнала флуктуируют по случайному негауссовскому закону распределения.

Все использующиеся в ММИС дискретные случайные сигналы удовлетворяют условиям физической реализуемости и допускают соответствующие полигауссовы представления при адекватном описании распределений их параметров:

w^j (u) = w¹ (u_},u₂ ... и_K) =

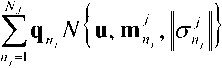
где AffuXjKI – гауссовское распределение, соответствующее ⁿj -ой компоненте вероятностной смеси, представляющ е й реальное распределение сигнала j -го типа; q – вектор весовых коэффициентов (вероятностей присутствия) ⁿj -ой компоненты; m^v„_;. – вектор математических ожиданий ⁿ i -ой компоненты; 1°""/1 – ковариационная матрица Hj -ой компоненты вероятностной смеси по всем K отсчетам.

Для сложного сигнально-помехового комплек- са, когда в групповом тракте имеет место наложение r независимых сигналов s.,sh ... Sj с номерами соответствующих им элементарных сигналов ^1 ^ Э • • • , а также импульсной помехи и АБГШ, возникает задача полного разрешения сигналов [4], для которой совокупная плотность распределения вероятностей для определенного интервала реализации определяется как многомерная свертка плотностей вероятностей сигналов и помех по всему множеству к-ых интервалов:

w¹^’^{11 1,,п}^ ^{x x} w^’'²

Тогда вследствие инвариантности гауссовских распределений относительно линейных преобразований наблюдаемый на входе вектор u также является полигауссовым:

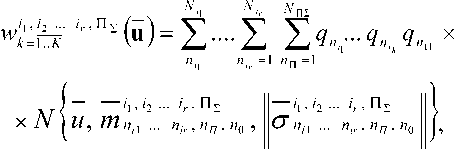
где гауссовские компоненты TV yj определяются свертками распределений, соответствующих гауссовским плотностям, линейными комбинациями которых представлены исходные (5) полигауссовы плотности интерферирующих сигналов и помех. Верхняя индексация означает принадлежность к сигнально-помеховой комбинации, а нижняя определяет принадлежность к номерам реализующихся в процессе приема гауссовских компонент сигналов ( ⁿir )’ помех («nJ и шума ( «0 )•

Синтез алгоритма разрешения сигналов и помех выполняется в соответствии с байесовским подходом, в рамках которого решающее правило относительно группы реализовавшихся сигналов при одинаковых рисках за неверно принятое решение и при одинаковых априорных вероятностях реализации сигналов выглядит как выбор комбинации, соответствующей максимальному значению совокупной плотности распределения вероятностей. Таким образом, решающее правило, определяющее наиболее вероятную совокупность реализовавшихся в векторе отсчетов u сигналов из ансамбля S, может быть записано следующим образом:

S,S, ... S, =arg max

,/| ’    /2             J_r          °    . e

<^'-ⁿJu). (8)

Исходя из перечисленных требований и условий к математическим моделям, можно сделать вывод о том, что использование новых посткорреляционных моделей позволяет в более полной мере (по сравнению с корреляционными) учитывать информационную и вероятностно-временную структуру широкополосных сигналов, особенности их распространения и уровень взаимных внутрисистемных помех в реальных радиолиниях CDMA-систем.

Это позволяет синтезировать новые, более эффективные алгоритмы совместной обработки сигналов в комплексе помех, адаптирующиеся к изменяющимся условиям работы базовых станций и параметрам СПО. Применение технологии полигауссового анализа и синтеза алгоритмов обработки многоэлементных сигналов на фоне комплекса негауссовских помех позволяет аналитически синтезировать оптимальные алгоритмы приема при произвольном характере флуктуаций сигналов и помех и приводит к унифицированным структурам алгоритмов приема, обладающих высокой степенью внутреннего параллелизма [12].

При практической реализации алгоритмов приема МЭС «в целом» весьма плодотворным является использование марковских моделей [13], которые обеспечивают ограничение сложности полигауссовых алгоритмов. Использование допущений о марковском характере взаимосвязи элементов сигнала позволяет ценой определенного сужения класса анализируемых случайных процессов обеспечить конструктивное представление взаимосвязи элементов сигналов и синтезировать рекуррентные процедуры их обработки.

В [11-12] показано, что использование вероятностных моделей, сочетающих свойства поли-гауссовых и марковских моделей (МС-ПГ), позволяет получать структуры алгоритмов приема многоэлементных сигналов, формируемых на базе конечной совокупности операций, соответствующих вычислению простейших гауссовских функционалов правдоподобия. При этом структурная сложность таких алгоритмов не зависит от размерности (количества позиций) принимаемых сигналов [11]. Уникальные свойства МС-ПГ моделей позволяют синтезировать новый класс проблемно-ориентированных алгоритмов и мультипроцессоров обработки многоэлементных сигналов, инвариантных к числу элементов сигналов и виду распределений негауссовских помех. Класс синтезированных алгоритмов показал возможность получения законченных аналитических решений, обеспечивающих получение достаточно простых форм синтезируемых алгоритмов и приводящих к унифицированным многоканальным параллельно-конвейерным структурам оптимальных и квазиоптимальных приемников [4-5]. Как результат это обуславливает возможность их эффективной и экономичной реализации на основе быстродействующих ПЛИС, устройствах функциональной микроэлектроники и унифицированных программно-аппаратных средствах.

Заключение

Предложен комплексный подход, объединяющий в единый процесс исследования комплекс взаимосвязанных частных задач, определяющих этапы разработки эффективных устройств обработки сигналов для широкого класса информационных систем. Представленная методика обеспечивает эффективное решение задач обработки сигналов в ММИС в негауссовских каналах благодаря корректному использованию адекватных посткорреляционных моделей каналов связи на основе смесей вероятностных распределений, разработке эффективных алгоритмов обработки МЭС и реализующих их сбалансированных мультипроцессорных вычислительных структур.

Универсальность посткорреляционных вероятностных моделей в отношении аналитического синтеза оптимальных и квазиоп-тимальных алгоритмов обработки сигналов в ММИС для гауссовских и негауссовских каналов позволяет получать адекватные исходной модели унифицированные многоканальные структуры алгоритмов обработки сигналов, обладающие свойством внутреннего параллелизма, инвариантные относительно широкого класса априорных распределений сигналов и помех.