Комптоновское рассеяние аттосекундных рентгеновских импульсов на многоэлектронных атомах

Методы генерации коротких и ультракоротких лазерных импульсов (УКИ) получили активное развитие в последние годы [1]. Уже сейчас с помощью лазеров на свободных электронах (XFEL) возможно получать УКИ с длительностями порядка 1фс, при этом непрерывно ведется работа, по их сокращению. Так, в работе [2] предложен метод генерации изолированных одноцикловых рентгеновских импульсов с длительностью 380 ас на. средней длине волны 8.6 нм. В статье [3] разработан подход, позволяющий генерировать субцикловые XFEL импульсы с длительностью 10.7 ас. Таким образом, указанные экспериментальные достижения делают актуальным теоретическое исследование взаимодействия аттосекундных рентгеновских импульсов с различными мишенями. В частности, значительный фундаментальный и практический интерес представляет анализ рассеяния УКИ на. атомах и ионах.

Томсоновское рассеяние УКИ различной формы на. свободном электроне анализировалось в работе [4] в нерелятивистском пределе. Было, в частности, показано, что полная

вероятность рассеяния УКИ для всех несущих частот является монотонно возрастающей функцией длительности импульса.

Резонансное рассеяние фемтосекундных УКИ на атомах в плазме рассчитывалось в статье [5], а упругое рассеяние аттосекундных рентгеновских импульсов на внутренних оболочках атомов исследовалось в работе [6]. В этих работах, в частности, было показано, что полная вероятность упругого рассеяния УКИ на атомах и ионах (за все время действия импульса) является, вообще говоря, нелинейной функцией длительности импульса даже в пределе слабого поля. Данное обстоятельство носит общий характер для всех фотопроцессов в поле УКИ [7, 8].

Переизлучение УКИ на атомах водорода и гелия рассматривалось в статье [9] в рамках приближения мгновенного возмущения, которое предполагает, что длительность импульса много меньше всех характерных атомных времен. В этом приближении связь электрона с ядром учитывается только атомным форм-фактором, что, вообще говоря, недостаточно для корректного описания зависимости вероятности фотопроцесса от всех параметров задачи в широком диапазоне их значений, в частности от длительности импульса.

В настоящей работе исследуется комптоновское рассеяние УКИ на атомах аргона, ксенона и натрия в терминах дифференциальной по углу и частоте вероятности фотопроцесса в зависимости от несущей частоты и длительности импульса, частоты рассеянной волны и угла рассеяния.

2.    Метод расчета

В статье [10] было показано, что в случае ультракоротких импульсов понятие вероятности фотопроцесса в единицу времени, которое традиционно применяется для описания электромагнитных явлений, имеет свои границы применимости. В связи с этим предлагается использовать полную вероятность процесса за все время действия УКИ (дифференциальную по углу и частоте), задающуюся следующим выражением [11]:

d²lK      с Г ^ da(ш,ш',Ө') | Е(ш,ш_с,т ) |²

d^'d^'   4т2 /о    d^'dw'         ш где с - скорость света, Е(ш,шс,т) - фурье-образ напряженности электрического поля в импульсе, ш - текущая частота, шс - несущая частота импульса, т - длительность импульса, ш' - частота рассеяиного излучения, Ө - угол рассеяния, dQ' - элемент телесного угла рассеяния излучения. Здесь и далее используем атомные единицы е = ~ = те = 1-

Спектрально-угловое сечение комптоновского рассеяния, входящее в правую часть формулы (1), можно представить в виде [12]:

Q(ш,ш,,q)

ш — ш' — q²/2 q

В настоящей работе для J(Q) используются данные, полученные в [13].

Дифференциальное по углу сечение томсоновского рассеяния монохроматического излучения на свободном электроне в нерелятивистском приближении равно

/ da \ dQ тһ

11 + СО82Ө

С4   2

(ш )2.

В качестве УКИ будем использовать так называемый скорректированный гауссовский импульс [14], квадрат модуля фурье-образ которого имеет вид

I Е(ш,ш_с,т ) |²

= Е0т² 1 (

ш2т 2

1 + ш2Т²

^ [ежр(-(ш

- шс)²т²) + ехр(-(ш + шс)²т²)] ,

где Ед - амплитуда напряженности электромагнитного поля в импульсе.

3.    Результаты расчетов и обсуждение

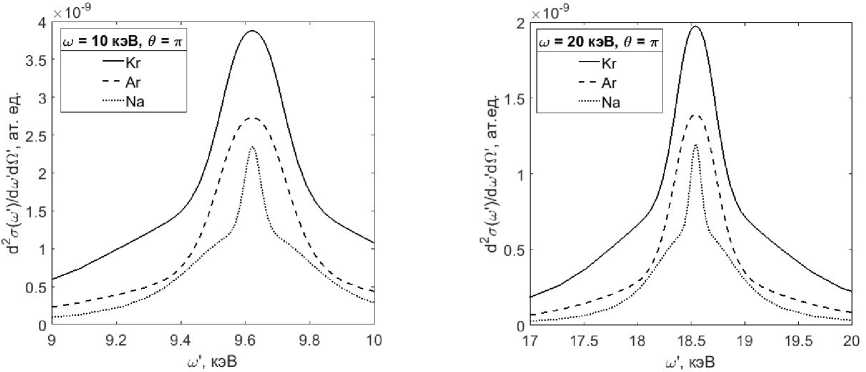
На рис. 1 приведены спектры дифференциального по частоте и углу сечения комптоновского рассеяния УКИ на атомах аргона, ксенона и натрия, вычисленные по формуле (2) при текущей частоте падающей волны ш = 10 кэВ (рис. 1а) и ш = 20кэВ (рис. 16) и угле рассеяния Ө = тг. Как видно из графиков, в случае атома натрия вклад валентного электрона характеризуется более острым пиком, нежели вклад остальных электронов на внутренних оболочках, поэтому мы наблюдаем своеобразный пьедестал в исследуемой зависимости.

а)

б)

Рис. 1. Спектрально-угловое сечение комптоновского рассеяния на. атомах аргона, ксенона, и натрия, вычисленное по формуле (2) при текущей частоте падающей волны ш = 10кэВ (а) ш = 20кэВ (б): сплошная линия - на. атоме криптона, штриховая линия - на. атоме аргона, пунктирная линия - на. атоме натрия

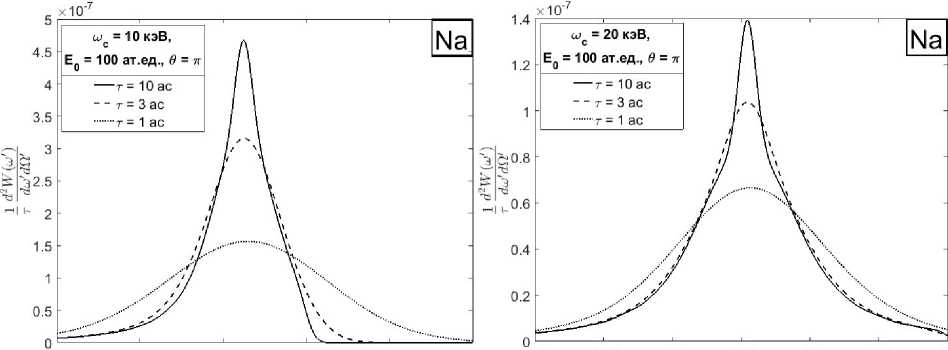
Вероятность комптоновского рассеяния УКИ рассчитана, для амплитуды напряженности электрического поля в импульсе Ед = 10²ат. ед. На рис. 2 представлен спектр дифференциальной по углу и частоте вероятности комптоновского рассеяния на атоме натрия за все время действия импульса, нормированный на длительность импульса, при несущей частоте ш_с = 10 кэВ (ри с. 1а) и ш_с = 20 кэВ (рис. 16), угле рассеяния Ө = ли различных длительностях т = 1, 3,10 ас. Как видно из графиков, зависимость имеет один максимум, амплитуда которого увеличивается с ростом длительности, при этом сам он становится уже. В случае ш_с = 10 кэВ зависимость имеет несимметричный характер, который проявляется сильнее с увеличением длительности импульса. С ростом значения несущей частоты несимметричность постепенно исчезает. На рис. 2а при ш_с = 20 кэВ и достаточно больших длительностях УКИ мы видим некую ступеньку, которая является следствием выполнения закона сохранения энергии.

На рис. 3, 4 представлены зависимости дифференциальной по углу и частоте вероятности комптоновского рассеяния на. атоме натрия за. все время действия УКИ от длительности импульса для несущей частоты ш_с = 10 кэВ, угла рассеяния Ө = ли различных значений частоты рассеянной волны ш‘ > ш_с (рис. 3) и ш‘ <  ш_с (рис. 4). При значениях частоты рассеянной волны больше несущей исследуемые зависимости имеют один максимум.

Амплитуда максимума с увеличением частоты падает, а его положение смещается в областв меньших длительностей. При частоте рассеянной волны меньше несущей частоты импульса зависимости имеют максимум и минимум в области т = 0.5-2 ас. Амплитуда максимума падает при уменьшении частоты рассеянной волны, при этом его положение смещается в сторону более коротких длительностей. При длительности УКИ т = 2-3 ас зависимость приобретает линейный вид, который хорошо описывается в рамках классического подхода. Аналогичные расчеты для других значиний несущих частот показали, что при увеличении значения несущей частоты воздействующего импульса указанные нелинейности становятся менее выраженными.

8.5          9          9.5          10         10.5         11       17       17.5       18       18.5       19       19.5       20

м', кэВ                                                              ш, кэВ

а)                                                         б)

Рис. 2. Спектр дифференциальной по углу и частоте вероятности комптоновского рассеяния за. все время действия импульса при несущей частоте ш_с = 10 кэВ (а) ш_с = 20 кэВ (б) и различных длительностях: сплошная линия - т = 1ас, штриховая линия - т = 3ас, пунктирная линия - т = 10 ас. Величина вероятности нормирована на длительность импульса

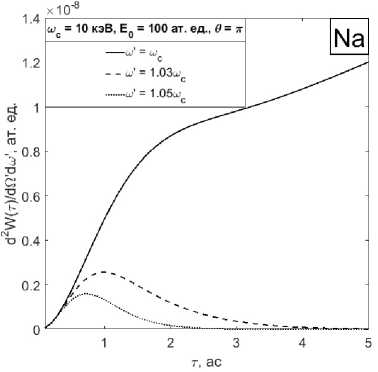
Рис. 3. Зависимость дифференциальной по углу и частоте вероятности комптоновского рассеяния на. атоме натрия за. все время действия УКИ от длительности импульса, для несущей частоты ш_с = 10 кэВ и различных значений частоты рассеянной волны: сплошная линия - ш ‘ = 10кэВ, штриховая линия - ш ‘ = 10.3кэВ, пунктирная линия - ш ‘ = 10.5 кэВ

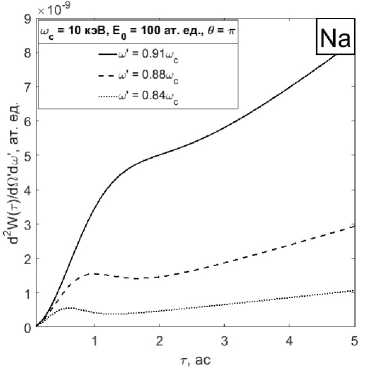
Рис. 4. Зависимость дифференциальной по углу и частоте вероятности комптоновского рассеяния на. атоме натрия за. все время действия УКИ от длительности импульса, для несущей частоты ш_с = 10 кэВ и различных значений частоты рассеянной волны: сплошная линия - ш‘ = 9.1 кэВ, штриховая линия - ш ‘ = 8.8кэВ, пунктирная линия - ш ‘ = 8.4 кэВ

На рис. 5, б представлены зависимости дифференциальной по углу и частоте вероятности комптоновского рассеяния на атоме натрия за все время действия УКИ от длительности импульса для несущей частоты ш_с = 10 кэВ и различных углов рассеяния Ө = тг, 2г, ^ при частоте рассеянной волны ш' > ш_с (рис. 5) и ш' < ш_с (рис. 6). Как видно из графиков, в случае, когда ш' > ш_с, амплитуда максимума зависимости достигает своей наибольшей величины при рассеянии на небольших углах относительно направления волнового вектора падающей волны. Наименьшее значение достигается при рассеянии под углом Ө = 2. В случае, когда ш' < ш_с, исследуемая величина приобретает свои наибольшие значения при рассеянии назад.

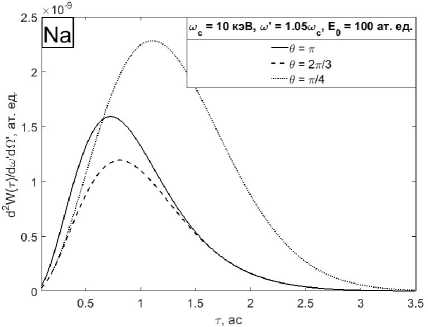
Рис. 5. Зависимость дифференциальной по углу и частоте вероятности комптоновского рассеяния на. атоме натрия за. все время действия УКИ от длительности импульса, для несущей частоты ш_с = 10кэВ, частоте рассеянной волны ш ‘ = 10.5 кэВ и различных углах рассеяния: сплошная линия - Ө = тг, штриховая линия -Ө = 23^, пуиктириая линия - Ө = (

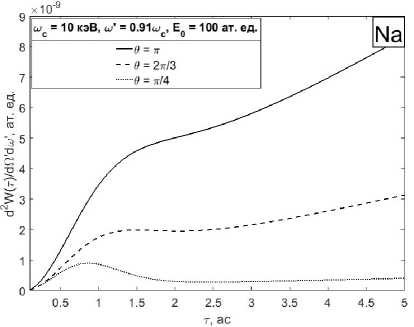
Рис. 6. Зависимость дифференциальной по углу и частоте вероятности комптоновского рассеяния на. атоме натрия за. все время действия УКИ от длительности импульса, для несущей частоты ш_с = 10кэВ, частоте рассеянной волны ш ‘ = 9.1 кэВ и различных углах рассеяния: сплошная линия - Ө = тг, штриховая линия -Ө = Ар • пуиктириая линия - Ө = (

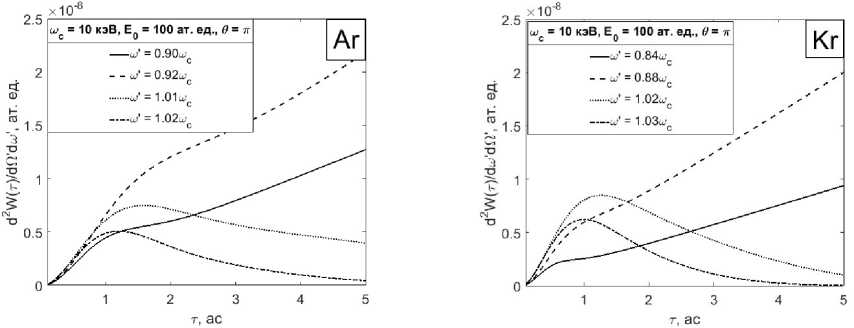
Рис. 7. Зависимость дифференциальной по углу и частоте вероятности комптоновского рассеяния на. атоме аргона, за. все время действия импульса. УКИ от длительности импульса, для несущей частоты ш_с = 10 кэВ и различных значений частоты рассеянной волны: сплошная линия - ш‘ = 9кэВ, штриховая линия - ш‘ = 9.2кэВ, пунктирная линия - ш ‘ = 10.1 кэВ, штрих-пунктирная линия - ш ‘ = 10.2 кэВ

Рис. 8. Зависимость дифференциальной по углу и частоте вероятности комптоновского рассеяния на. атоме криптона, за. все время действия импульса. УКИ от длительности импульса для несущей частоты ш_с = 10 кэВ и различных значений частоты рассеянной волны: сплошная линия - ш ‘ = 8.4кэВ, штриховая линия - ш ‘ = 8.8кэВ, пунктирная линия - ш‘ = 10.2кэВ, штрих-пунктирная линия - ш ‘ = 10.3 кэВ

На рис. 7, 8 приведены зависимости дифференциальной по углу и частоте вероятности комптоновского рассеяния за все время действия импульса УКИ от длительности импульса на атомах аргона и криптона для несущей частоты ш_с = 10кэВ, угла рассеяния Ө = т и различных значений частоты рассеянной волны ш' >  ш_с и ш' < ш_с. Как видно из графиков, для атомов благородных газов наблюдаются зависимости, аналогичные зависимостям в случае натрия. При значениях частоты рассеянной волны больше несущей наблюдается один максимум, в то время как при частоте рассеянной волны меньше несущей мы имеем нелийнейность с максимумом и минимумом в области т = 0.5-2 ас. Амплитуда максимумов падает при увеличении отстройки частоты рассеянной волны от несущей, при этом положение максимумов смещается в область более коротких длительностей.

4.    Заключение

В работе теоретически исследовано комптоновское рассеяние аттосекундных рентгеновских импульсов на атомах благородных газов (аргоне и криптоне) и атоме натрия в зависимости от несущей частоты и длительности импульса, частоты рассеянной волны и угла рассеяния. Рассмотрение проводилось в терминах спектрально-угловой вероятности рассеяния за все время действия импульса. Для всех рассматриваемых мишеней получены зависимости с аналогичными характеристиками.

Показано, что спектр дифференциальной по углу и частоте вероятности комптоновского рассеяния за все время действия импульса представляет собой зависимость с одним максимумом, амплитуда которого увеличивается с ростом длительности, при этом сам он становится уже. Зависимость имеет несимметричный характер, который становится менее выраженным с уменьшением длительности и увеличением несущей частоты импульса.

Зависимость дифференциальной по углу и частоте вероятности комптоновского рассеяния за все время действия УКИ от длительности импульса в области ш' >  ш_с (частота рассеянной волны больше несущей частоты импульса) представляет собой структуру с одним максимумом, в то время как в области ш' <  ш_с (частота рассеянной волны меньше несущей частоты импульса) наблюдается нелинейность с максимумом и минимумом при т = 1-2 ас, а при длительности УКИ т = 2-3 ас зависимость приобретает линейный вид, который хорошо описывается в рамках классического подхода. Амплитуда максимумов падает с ростом отстройки величины рассеянной волны от несущей, при этом положение максимумов смещается в область более коротких длительностей. При увеличении значения несущей частоты воздействующего импульса указанные нелинейности становятся менее выраженными.

Зависимость дифференциальной по углу и частоте вероятности комптоновского рассеяния за все время действия УКИ от угла рассеяния неодинакова для рассматриваемых областей ш' > ш_с и ш' <  ш_с. В первом случае амплитуда максимума зависимости достигает своей наибольшей величины при рассеянии на небольших углах относительно направления волнового вектора падающей волны. Наименьшее значение достигается при рассеянии под углом Ө = 2- Во втором случае исследуемая величина приобретает свои наибольшие значения при рассеянии назад.

Работа выполнена в рамках Государственного задания Министерства науки и образования РФ (задание № 3.9890.2017/8.9).