Комптоновское рассеянное излучение в рентгеновском анализе веществ сложного химического состава

Непрерывное совершенствование технологий получения самых разнообразных материалов и интенсификация производственных процессов обуславливают необходимость разработки высокоскоростных и высокоточных методов контроля химического состава перерабатываемой продукции.

Особый интерес в этом плане представляют различные рентгенофизические методы анализа; экспрессность, простота и возможность осуществления анализа без непосредственного контакта с образцом выгодно отличают их от традиционных методов аналитической химии.

Флуоресцентный рентгенорадиометрический метод (РРМ) является разновидностью рентгеноспектрального метода анализа (РСА). Отличительной особенностью РРМ является возбуждение «К» или «L» — серии рентгеновских спектров атомов ионизирующим излучением радионуклида. Выделение аналитической линии из вторичного спектра осуществляется без его разложения на кристалл-анализаторе. Поэтому аппаратура РРМ-метода отличается компактностью и простотой обслуживания [11, 21].

Для флуоресцентного рентгеноспектрального анализа (РСА) характерны те же закономерности, что и для рентгенорадиометрического анализа. РСА основывается на возбуждении флуоресцентного (вторичного) излучения анализируемого вещества первичным рентгеновским излучением. В отличие от РРМ-метода возбуждение «К» или «L» — серии рентгеновских спектров атомов осуществляется тормозным рентгеновским излучением и характеристическим излучением вещества анода рентгеновской трубки [11, 17].

Выделение аналитической линии из вторичного спектра осуществляется как с разложением на кристалл-анализаторе, так и без его разложения. И методы РСА, и методы РРМ относятся к рентгенофлуоресцентному анализу (РФА), поэтому в дальнейшем, без особой на то необходимости, будут обозначаться как РФА.

Дальнейшее развитие РФА связанно как с совершенствованием метрологических параметров спектрометров и разработкой высокоэффективных детекторов, так и с усовершенствованием уже существующих и разработкой новых способов учета влияния химического состава вещества (матричный эффект) на результаты анализа, являющегося основным источником систематической погрешности РФА. В ряде случаев влияние матричного эффекта настолько существенно, что проведение анализа с необходимой точностью не представляется возможным. Так, при анализе проб с сильно меняющимся химическим составом, например, минерального сырья, промышленных отходов, промпродуктов, концентратов и т.п., погрешность анализа сопутствующих элементов может достигать десятков и даже сотен процентов относительных [11].

При поиске, разведке и разработке месторождений нефти и газа актуальнейшей проблемой является повышение степени извлечения полезной информации из геологических, геофизических и геохимических данных исследований минерального сырья, горных пород и почв. Эта задача решается различными методами, среди которых большое развитие получили рентгенографические благодаря относительной простоте, высокой точности и объективности анализа. Но при применении дифракционного рентгенофазового анализа (РФЗА) возникает та же проблема — влияние минералогического состава пробы на результаты анализа — матричного эффекта [1]. Таким образом учет матричного эффекта является важнейшей задачей и для РФА и для РФЗА.

В данной работе автором показано новое направление рентгенофизического анализа, интегрирующее рентгенофазовый и рентгенофлуоресцентный методы анализа с использованием некогерентно рассеянного Комптоновского излучения.

2.    Рентгеновский флуоресцентный анализ

Как уже говорилось ранее, главная проблема, с которой приходится сталкиваться при использовании рентгенофлуоресцентных методов, — это зависимость результатов определения от химического состава пробы.

Наибольшее распространение среди известных инструментальных методов учета матричного эффекта при РРМ получил способ спектральных отношений, впервые предложенный В.А.Мейером и В.С.Нахабцевым для анализа тяжелых элементов. По сути, это модификация метода стандарта-фона, предложенного Андерманом и Кемпом для рентгеноспектрального анализа. В качестве аналитического параметра в данном методе используется отношение интенсивностей характеристического излучения определяемого элемента и некогерентно рассеянного пробой первичного излучения [20, 26].

Исследованиям по использованию способа спектральных отношений посвящено множество работ [3, 4, 16, 18, 19, 21—25, 27], однако проблема учета матричного эффекта до сих пор решена не полностью.

Для пояснения сущности предложенного способа анализа рассмотрим более детально способ спектральных отношений.

Поток характеристического излучения J i , возникающий при облучении анализируемой пробы параллельным монохроматическим пучком рентгеновского или γ -излучения с энергией выше энергии К-края поглощения анализируемого элемента, описывается следующим выражением [8]:

J S - 1 С

Ji = 02 η S K pk τm × (1- exp[-(µi/sinϕ+µ0/sinψ) m ]), (1) 4πR SK µi / sinϕ+ µ0 / sinψ где R — расстояние от поверхности пробы до детектора; S — площадь исследуемой пробы; η — коэффициент выхода флуоресценции; pK — вероятность перехода атома, возбужденного на K-уровень с испусканием характеристического излучения i-линии; SK — величина К (или L)-скачка поглощения анализируемого элемента; τM — массовый коэффициент фотоэлектрического поглощения первичного излучения определяемого элемента; µ i и µ 0 — массовые коэффициенты поглощения характеристического и первичного излучений исследуемой пробы соответственно; m — поверхностная плотность пробы;ϕ , ψ — углы скольжения к поверхности пробы характеристического и первичного излучений соответственно; С — массовая концентрация анализируемого элемента.

С увеличением энергии фотонов эффективность возбуждения флуоресцентного излучения резко уменьшается, так как массовый коэффициент фотоэлектрического поглощения τ M пропорционален E - Р , где р ≈ 3 в области энергий до 100—120 кэВ.

В зависимости от значений поверхностной плотности различают методики измерений в тонких и насыщенных слоях. Для тонких слоев поверхностная плотность настолько мала, что выполняется неравенство ( µ i / sin ϕ + µ 0 / sin ψ ) т << 1 и можно применить приближенную формулу: е^-x ≈ 1 – х.

Тогда выражение (1) примет вид:

J i = J ⁰ ₂ η S S^K 1 p k τ m С m. (2) 4 π R S K

Из этого выражения видно, что при постоянной поверхностной плотности имеет место прямая пропорциональность между потоком характеристического излучения и концентрацией анализируемого элемента. Однако реализация этого метода в приборах экспресс-анализа затруднена в связи с необходимостью приготовления очень тонких слоев, особенно при анализе элементов с Z < 35 ÷ 40, когда поверхностная плотность должна быть меньше 5 мг/см².

Методика анализа в насыщенных слоях предусматривает проведение измерений, когда поверхностная плотность пробы достаточно велика и выполняется неравенство exp[- ( µ i / sin ϕ + µ 0 /sin ψ ) m ] << 1.

Тогда выражение (1) принимает следующий вид:

J i = J ⁰ 2 η S S^{K -} 1 p k τ m С . (3) 4 π R S K µ i /sin ϕ + µ 0 /sin ψ

Знаменатель в общем случае зависит от концентрации анализируемого элемента, причем зависимость интенсивности потока J i от концентрации анализируемого элемента не линейна. Поэтому на практике обработка результатов измерений проводится графически на основании градуировочной зависимости J i = f (С эт ) , построенной по образцовым эталонным пробам с известным содержанием анализируемого элемента.

Значения массовых коэффициентов поглощения µ i и µ 0 также зависят от вещественного состава наполнителя. Поэтому методика анализа в насыщенных слоях по измерению интенсивности аналитической линии определяемого элемента обеспечивает достаточно высокую точность анализа лишь в том случае, когда вещественный состав наполнителя изменяется незначительно.

Преобразуем (3) с учетом аддитивности массовых коэффициентов поглощения:

J i =

J ₀

4 π R ²

S - 1                             С

η S ^K    p k τ m                                                    , (4)

S K        [ µ _iaC + µ _iM (1 - C )]/sin ϕ + [ µ _{0 a}C + µ _{0 M} (1 - C )]/sin ψ

где µia и µiм массовые коэффициенты поглощения характеристического излучения анали- зируемым элементом и наполнителем пробы соответственно; µ0a и µ0м массовые коэффи- циенты поглощения первичного излучения анализируемым элементом и наполнителем пробы соответственно.

С учетом пропорциональности массового коэффициента поглощения Е ^–3

µ 0a / µ ia = S k (E i /E 0 )³; µ 0м / µ iм = (E i /E 0 )³                        (5, 6)

и окончательно уравнение (4) можно записать в следующем виде:

Ji=  0 ηSSK - pkτm

4 π R ²        S                ( E / E )³    1                ( E / E )³ 1

K           µ0aC[  0 i +      ]+µ0M(1-C)[ 0 i +

S k sin ϕ  sin ψ              sin ϕ sin

Преобразуем выражение (4) для интенсивности характеристического излучения, возникающего в «толстом» образце [17]:

Ji=КiCa/[(µоa/sinψ+µia/sinϕ)Ca+(µoм/sinψ+µiм/sinϕ)Cм ],(8)

где К = 0 ηS K - p τ — коэффициент пропорциональности, не зависящий от хими-4πR2

ческого состава пробы и геометрии измерения; C a и C м — содержание определяемого элемента и элементов наполнителя пробы (C a + C м = 1 ).

Рассмотрим некогерентно рассеянное по Комптону первичное излучение, массовый коэффициент рассеяния которого слабо зависит от эффективного атомного номера наполнителя [18]. Это объясняется тем, что при некогерентном рассеянии фотон взаимодействует с отдельными электронами, число которых в единице массы равно N А Z/A , где N A — число Авогадро, Z — порядковый номер элемента, А — атомная масса. То есть массовый коэффициент рассеяния практически не различается для различных элементов.

Аналогично (8) выражение для интенсивности некогерентно рассеянного от пробы первичного излучения имеет вид [16]:

J 2 = К 2 / [ ( µ оa / sin ψ + µ 2a / sin ϕ )C a +( µ oм / sin ψ + µ 2м / sin ϕ )C м ],      (9)

где К 2 = 4 R 0 2 σ S α — коэффициент пропорциональности, не зависящий от химического состава пробы и геометрии измерения; σ — массовый коэффициент некогерентного рассеяния первичного излучения в пробе; α — коэффициент анизотропии углового распределения некогерентно рассеянного излучения; µ 2а и µ 2м — массовые коэффициенты поглощения рассеянного излучения соответственно в определяемом элементе и наполнителе.

Выражение для аналитического параметра в способе спектральных отношений будет иметь вид:

= J 1 = K i C a / [ ( р оа / Sin ^ + р а / sin ф )С а +( ^ ом / sin ^ + р sin ф )C , ] J 2     К 2 / [ ( р оа / sin ^ + p 2a / sin ф J C a + р о , / sin 1// + p 2, / sin ф )С м ]

.

С использование соотношений (5, 6) и с учетом р _Оа « р _2аи р _Ом « р _2м выражение (10)

примет вид:

^[ р о _aC _a( ^{1 /Si}W ^{+ 1 /Sin} У ) ⁺ р о м^См^{( 1} / ^Sin Ф ^{+ 1} / ^Sin У ) ^] С д

К п = —-             ,                                   ,                ,

К 2 р о C [ (E o /E i )/ ( S_k Sin ф ) + 1/Sin у ] + р о C , [( Е о / E i ) ³ / Sin ф + 1 / Sin у ]’

где Е i и Е o — энергии характеристического и некогеpентно рассеянного излучений.

Полученное выражение определяет зависимость отношения интенсивностей характеристического и рассеянного излучений для метода спектральных отношений от массового коэффициента поглощения пробы при выбранной энергии первичного излучения.

Из выражения (11) следует, что метод спектральных отношений при анализе элементов средней группы периодической таблицы устраняет влияние вещественного состава наполнителя весьма эффективно только в области малых C _а « О или больших концентраций C _а ® 1 определяемого элемента, когда можно пренебречь соответственно первыми или вторыми слагаемыми числителя и знаменателя. В остальной же области концентраций, для элементов средней группы периодической таблицы, зависимость результатов анализа от изменения матрицы сохраняется.

3.    Рентгеновский флуоресцентный анализ с использованием дополнительного поглотителя

Как видно из выражения (11), что подтверждается экспериментальными данными, аналитический параметр п (для проб равной концентрации определяемого элемента С_а — Const , но с различным химическим составом и значениями р _м ), нелинейно убывает с ростом массового коэффициента поглощения первичного излучения в наполнителе пробы при выбранной энергии первичного излучения (рис. 1).

Группе авторов ИЯФ АнУзССР и филиала ВНИИТС УзКТЖМ принадлежит идея способа учета матричного эффекта с использованием вспомогательного поглотителя из анализируемого вещества при РРМ [2].

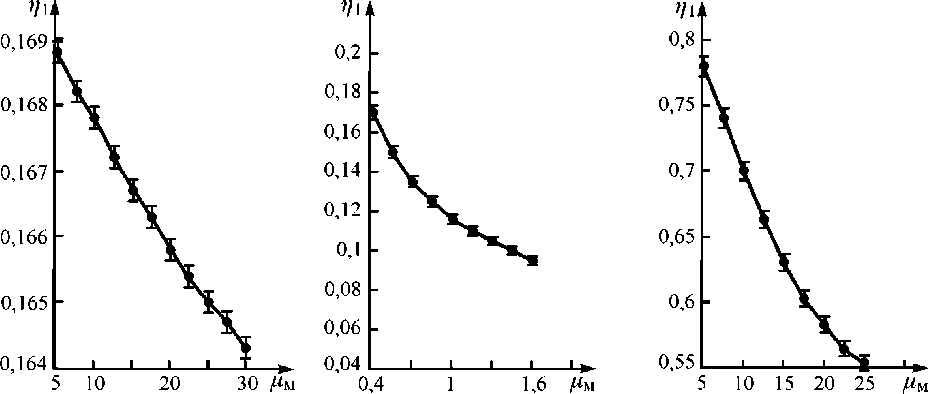
а)                                     б)                                     в)

Рис. 1. Зависимость аналитического параметра п от массового коэффициента поглощения наполнителя пробы р _м при определении W в его концентратах, отходах с источником Cd-109 (а); Мо в его концентратах с источником Am-241 (б); Со в его промпродуктах с источником Pu-238 (в)

Сущность способа в предлагаемом варианте рентгенорадиометрического анализа состоит в следующем.

Для компенсации неодинакового изменения J и J 2 в выражении (11) при изменении состава наполнителя пробы в схему измерения способа спектральных отношений вводится вспомогательный поглотитель, приготовленный из анализируемого вещества с некоторой поверхностной плотностью d , который устанавливают на пути рассеянного излучения между образцом и детектором при регистрации J 2 (рис. 2) [2, 14, 15].

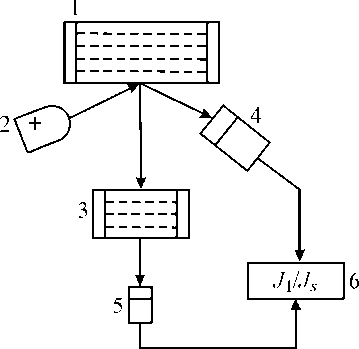
Рис. 2. Схема измерения с использованием дополнительного поглотителя: 1 — образец; 2 — источник изучения; 3 — поглотитель из анализируемого вещества;

4 — детектор изучения; 5 — детектор излучения; 6 — блок регистрации

В этом случае выражение для аналитического сигнала имеет вид:

П 1 = J 1 /J 2 exp[ -( Ц 2а С а + Ц 2м С мЖ                      (12)

где d — поверхностная плотность поглотителя, г/см².

При определенных условиях неодинаковые изменения J 1 и J₂ при вариациях поглощательной способности наполнителя могут быть частично или полностью скомпенсировано экспоненциальным членом этой функции.

Причем учет матричного эффекта происходит с достаточной эффективностью, так как величины ц эфф . и d , относящиеся к поглотителю, как видно из формулы (12), входят в показатель степени экспоненциального члена, который при найденных оптимальных условиях «компенсирует» дополнительное приращение J₂ , обусловленное сомножителем (E o /E i )³.

На рис. 3 приведены зависимости, иллюстрирующие степень учета матричного эффекта предлагаемым способом (1) и способом стандарта-фона (2).

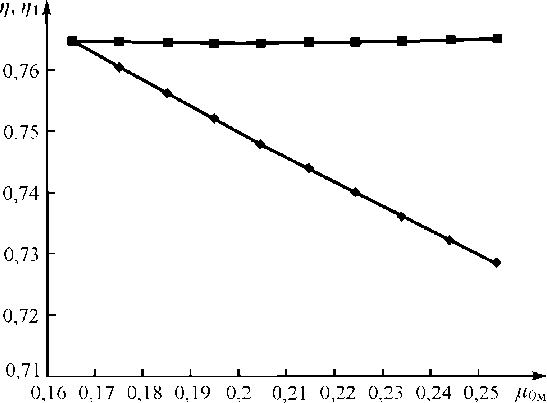
Рис. 3. Зависимости аналитических параметров от поглощательной способности наполнителей (значения параметров нормированы относительно друг друга):

1 — способ стандарта-фона, η ( μ _{0 м} ); 2 — предлагаемый способ, η ₁ ( μ _{0 м} )

Расчеты выполнены по формулам (11) и (12) для измерений выполненных при условиях: Z a =74, Z_м =15-25, С_а=С_м =0,5 (в отн. ед.), ф =90 o , у =45 o , E i =60 кэВ (Wk) и E o =100кэВ (максимум некогеpентно рассеянного излучения радионуклида Se-75), d = 1,2 г/см² [5].

Относительные отклонения значений аналитического сигнала по предлагаемому способу и по способу стандарта-фона составили 0,2% и 7,0% соответственно.

В способе с дополнительным поглотителем в качестве аналитического параметра берется отношение интенсивности аналитической линии определяемого элемента в прямом измерении (без поглотителя) к интенсивности некогерентно рассеянного пробой первичного излучения, прошедшего через дополнительный поглотитель:

J = К          [ А ) a C a ( 1 / Sin Ф + 1 / Sin У ) + А О м С м ( 1 / Sin Ф + 1 / Sin У ) ] С

J 2     К 2 ц С [ (E₀/EJ 3 / ( S k Sin Ф ) + 1 / Sin У ] + А о м С м [( E o I E i ) ³ 1 Sin ф + 1 / Sin у ]

X exp[ ( A o а С а + Ц 0 м С м )d] .

Как следует из выражения и подтверждается экспериментальными данными, аналитический параметр ц 1 как функция от переменной величины ц _{0 м} при фиксированных значениях С_а , С_м , ц _0м , при выбранной энергии первичного излучения имеет вид кривой с минимумом, зависящим от поверхностной плотности поглотителя d (рис. 4).

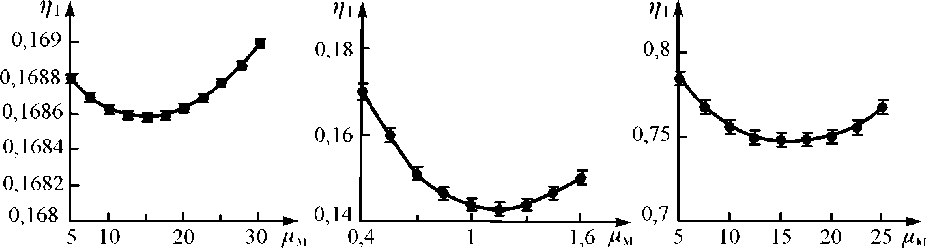
а)                               б)                                     в)

Рис. 4. Зависимость аналитического параметра η 1 от массового коэффициента поглощения наполнителя пробы μ м при определении: W в его отходах с источником Cd-109 (а); Мо в его концентратах с источником Am-241 (б); Со в его промпродуктах с источником Pu-238 (в); значения параметров η 1 нормированы относительно параметров η

Главным недостатком исследуемого способа была необходимость подбора поверхностной плотности поглотителя опытным путем для каждого конкретного случая.

Проблема здесь заключалась в том, что для каждой конкретной пробы с неизвестным значением коэффициента поглощения ц _0м приходилось подбирать опытным путем поверхностную плотность поглотителя d , соответствующую минимуму аналитического параметра, сменой нескольких поглотителей с различной поверхностной плотностью.

Для устранения этого недостатка, снижающего экспрессность и точность способа, автором данной работы найдена возможность расчета для каждой конкретной пробы точного значения поверхностной плотности поглотителя, соответствующего наиболее полному учету матричного эффекта [7].

Как уже говорилось, наиболее полный учет матричного эффекта происходит в области минимума аналитического параметра п1. Взяв производную от п1 по ц м при фиксированных прочих параметрах и приравняв ее к нулю, после определенных преобразований можно выразить поверхностную плотность d как функцию от интенсивностей аналитической линии определяемого элемента Ji и некогерентно рассеянного первичного излучения J2

в прямом измерении:

d = ^{J 1 J 2}

ц _0a(1/sin ф + 1/sin y )(E₀/E i )³(1-1/Sk , _L)/sin Ф .

K 1 K 2

Так как при взятии производной величина d также фиксировалась, то предполагалось использование одного поглотителя для проб в интервале изменения коэффициентов поглощения от минимального до максимального. Как видно из последнего выражения, для любой пробы можно рассчитать оптимальное значение поверхностной толщины поглотителя d , соответствующее максимальному учету матричного эффекта в рассматриваемом интервале, полагая, что проба находится в середине интервала изменения поглощательной способности проб.

Но внутри выбранного интервала изменения ц _0м величина аналитического параметра П 1 пусть незначительно, но изменяется. Автору удалось получить выражение, позволяющее определять такую величину поверхностной плотности поглотителя для любой неизвестной пробы, которая дает постоянную величину аналитического параметра п 1 ( Ц 0м ) = Const [11]. В этом случае d является переменной величиной внутри рассматриваемого интервала.

Представив аналитический параметр в виде:

^п 1 ⁿ ex^p[ ( ^ц 2а С а + ^ц 2M ^C M )d] ,

фиксируя П 1 = П 0, (где П 0 = П( Ц 0м min)) с учетом Ц 2а * Ц 0а и Ц 2м * Ц0м можно выразить d следующим образом:

d =

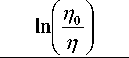
^Ц 0 а^Са ^{+ Ц} 0 м^См

Полученное выражение позволяет без выполнения измерений вывести формулы для расчета значений поверхностной плотности поглотителя и для эталонов, и для неизвестных проб по прямым измерениям без поглотителя. В первом случае в уравнение (18) необходимо подставить выражение (11) для аналитического параметра в способе стандарта-фона п. Во втором случае, используя выражение (9), с учетом ц 2а * ц 0а и ц 2м * ц 0м по- лучим:

= ^Кр

( С Ц оа ⁺ С м И ом ) .

--1--

81п ф Sin y

Из (18) и (19) окончательно для d получаем:

d =

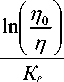
Г ^{1        1} 1

J p I--+--I .

( Sin ф Sin y J

Полученное выражение позволяет для любой пробы по измеренным интенсивностям характеристического J i - и некогерентно рассеянного J p -излучений рассчитать точное значение поверхностной плотности поглотителя, при использовании которого происходит полный учет матричного эффекта. Аналитический параметр для различных проб с постоянным содержанием определяемого элемента, но изменяющейся поглощательной способностью в этом случае является постоянной величиной.

На рис. 5 показаны зависимости аналитических параметров от поглощательной способности наполнителя проб для различных способов на примере определения Мо в Мо-концентратах на источнике Am-241 ( E i =17,5 кэВ, E 0 =62 кэВ, С а =0,3, м_0а = 4,3 см²/г, м_0м = 0,4 ^ 1,6 см²/г).

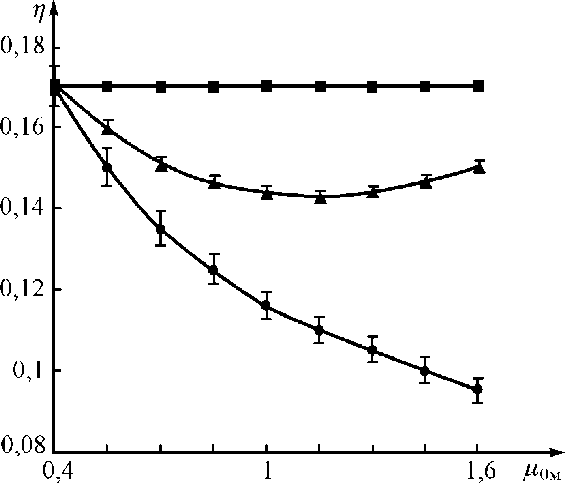
Рис. 5. Зависимости аналитических параметров от м 0м при определении Мо в молибденовых концентратах: • — для способа стандарта-фона; ▲ — для способа с одним поглотителем для всех проб интервала изменения µ 0м ; ■ — для способа с индивидуальным поглотителем для каждой пробы

Как видно из выражений и рисунка, систематическая погрешность при использовании поглотителей для проб со значениями поверхностной плотности, рассчитанными по выражению (20), равна нулю. Зависимость п 1 ( Ц 0м ) = П о является прямой.

Из вышесказанного следует, что наиболее просто рассматриваемый способ реализуется для энергодисперсионных методов РФА, характеризующихся высоким энергетическим разрешением спектрометрической аппаратуры. В качестве детекторов в этом случае используются полупроводниковые детекторы, в основном кремний-литиевые, позволяющие эффективно разрешать характеристические линии различных элементов, линии когерентного и некогерентного рассеяния первичного излучения.

3.    Рентгеновский фазовый анализ

В основе всех методов количественного фазового анализа лежит следующее фундаментальное уравнение [21]:

Ii = Ki xi  , n ∑∗ xiµi i=1

где I i — интенсивность некоторого выбранного рефлекса фазы i ; K i — экспериментальная по стоянная, зависящая от энергии первичного пучка, структуры анализируемой фазы, индексов (hkl) и условий съемки; ^Ц i * — массовый коэффициент поглощения фазой i первичного излучения; x i — содержание (массовая доля) фазы i в пробе; ^р i — плотность фазы i . Массовый коэффициент поглощения не зависит от агрегатного состояния вещества.

При выводе формулы (21) предполагалось, что дифракция происходит от поверхности плоского образца (съемка на отражение), который представляет собой однородную смесь п компонентов, причем толщина образца бесконечна.

При использовании энергодисперсионного детектора снимаемый спектр, кроме дифракционных пиков, представляющих когерентно рассеянное пробой первичное монохроматическое излучение, включает пики характеристического излучения элементов пробы, возбуждаемых первичным излучением, и некогерентно рассеянное пробой первичное монохроматическое излучение. Причем когерентная составляющая состоит из рассеянного по Брэггу и рассеянного по Томсону первичного излучения, в то время как некогерентная составляющая — из рассеянного по Комптону первичного излучения. Проведенные автором исследования показали существование определенной корреляции между интенсивностями вышеуказанных излучений.

Как показывает анализ выражений (21) и (9), интенсивность излучения определяемой фазы, как и интенсивность некогерентно рассеянного излучения, убывают с ростом поглощающей способности анализируемой пробы. При значительном росте массового коэффициента наполнителя пробы интенсивности могут уменьшаться в несколько раз, что приводит к относительной ошибке определения содержания того или иного компонента (при использовании интенсивности в качестве аналитиче ского параметра) в несколько сот процентов. Опыт показывает, что интенсивности рефлекса анализируемой фазы и рассеянного излучения незначительно отличаются на всем рассматриваемом интервале изменения поглощающей способности наполнителя.

Для проб с постоянным содержанием определяемой фазы, с ростом массового коэффициента поглощения наполнителя пробы интенсивности когерентно и некогерентно рассеянного излучения убывают практически одинаково c ростом массового коэффициента поглощения. Следовательно, отношение вышеуказанных интенсивностей практически не зависит от матрицы пробы [11].

Так как при снятии дифрактограммы углы скольжения и отбора равны, то в рассматриваемом случае выражение (9) можно представить как:

I p =K p /[( Ц оа + Ц 2a )C a + ( Ц ом + Ц 2м )С м ]. (22)

А с ^учетом Ц оа ~ Ц 2а и ^Ц ом ~ ^Ц 2м •

I p

K p

Ц 0 a ^C a ⁺ Ц 0 м ^С м

= K '

Е "С

i = 1

k где суммирование в Е м0iCi ведется по числу элементов пробы — k i=1

Как видно, полученное выражение аналогично выражению (21). Если в качестве аналитического параметра п взять отношение Ii/Ip, то с учетом того, что массовый коэффици ент поглощения первичного излучения не зависит от агрегатного состояния вещества, т.е.

kn

Е ^м о-^С. = р Е x ^Ц , i = 1                             i = 1

получим линейную зависимость аналитического параметра от содержания фазы i в пробе:

п = K i X i I K p ,

где Xi — содержание измеряемой фазы.

Таким образом, можно утверждать следующее: предположение о том, что отношение I i /I p незначительно зависит от матрицы пробы и может использоваться как аналитический параметр, теоретически обосновано. Данный теоретический вывод подтверждают и экспериментальные исследования [6, 8, 10].

4.    Заключение

Техническая реализация предлагаемого способа в силу своей простоты легко осуществима на дифрактометрах с энергодисперсионными детекторами, которыми могут оснащаться современные дифрактометры. Например, автоматический дифрактометр нового поколения ДРОН-7 оснащен Si(Li)-детектором с термоэлектрическим Пельтье-охлаждением, энергетическое разрешение которого в диапазоне от 2 кэВ до 30 кэВ не превышает 300 эВ при эффективности не менее 98%.

Сначала по стандартной схеме (рис. 6) снимается дифрактограмма анализируемой пробы (например, шлиф полевого шпата). Определяется точное положение наиболее интенсивной реплики определяемой фазы (например, 2 0 002 = 28,0 о ). Детектор устанавливается на данный угол дифракционного максимума измеряемой фазы, одновременно регистрируются интенсивность излучения измеряемой фазы, интенсивность некогерентно рассеянного по Комптону первичного излучения и интенсивность характеристического излучения определяемого элемента (элементов) измеряемой фазы (в данном примере Na, что позволяет идентифицировать полевой шпат как альбит). Концентрацию определяемого элемента в анализируемой пробе устанавливают по отношению интенсивностей характеристического излучения определяемого элемента измеряемой фазы и некогерентно рассеянного (по Комптону) этой же пробой первичного излучения. Концентрацию определяемой фазы данного элемента в анализируемой пробе устанавливают по отношению интенсивностей когерентно рассеянного (по Брэггу) определяемой фазой первичного излучения и некогерентно рассеянного (по Комптону) этой же пробой первичного излучения.

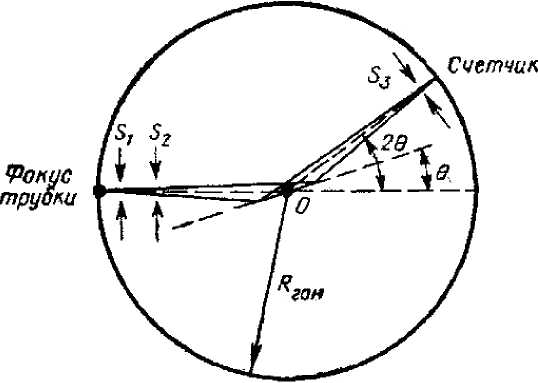
Рис. 6. Схема хода лучей в гониометре при снятии дифрактограммы.

В качестве счетчика в рассматриваемом способе используется энергодисперсионный детектор

Из вышесказанного следует, что в данном методе существенно повышаются объем и качество получаемой информации. Одновременно определяют и содержание интересующей нас фазы, и содержание входящих в нее элементов, причем с устранением матричного эффекта, что позволяет наряду с повышением экспрессности повысить точность определений. Например, матрица основных коллекторов Западной Сибири состоит из кварца, плагиоклазов (Ca-Na полевые шпаты), К полевых шпатов. Но недостатком рентгеноструктурного анализа является невозможность по репликам отличить эти компоненты. Поэтому в результатах они представляются вместе, а их разделение обычно проводят по соотношениям, определяемым при описании шлифов. В предлагаемом способе содержания плагиоклазов и калиевых полевых шпатов сравнительно легко определяются по измеренным содержаниям Ca, Na и K.

Предложенный способ защищен патентом Российской Федерации [9].