Концентрация напряжений в слое тканого композита с закрытыми внутренними технологическими порами

При производстве тканых композитов с искривленными волок-нами неизбежны технологические дефекты, снижающие эксплуатаци-онные свойства изделий. К числу типичных дефектов относятся возни-кающие при прошивке слоев разрывы нитей основы или утка, а также внутренние поры, которые возникают в областях, расположенных вблизи участков волокон с наибольшей кривизной (рис. 1), и обнару -живаются только на этапе выходного ультразвукового контроля изде-ЛИЯ. Эти области труднодоступны для проникновения полимерного связующего даже при условии вакуумирования или пропитки под дав-лением [1].

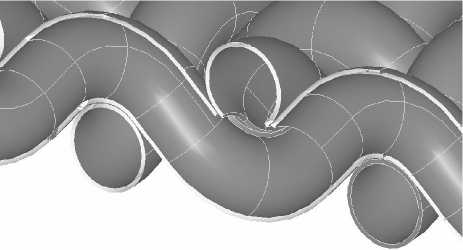
Рис. 1. Локальный дефект слоя тканого композита

Кроме того, обеспечение в этих участках наличия поликристалличе-ской матрицы, осаждаемой из газовой фазы или при карбонизации по-лимеров, также затруднено.

1.    Геометрическая модель

В качестве объекта исследований выберем слой тканого компози-та толщиной 2,5 D ( D ‒ диаметр круглых в поперечном сечении воло-кон). Искривление нитей основы и утка зададим двумя участками: -гой окружности радиусом 4 D ( c 2 D ) центральным углом а = л/4и прямой [2]. Будем предполагать, что искривленные волокна, принад-лежащие слою тканого композита с идеальной периодической струк-турой, всегда окружены гарантированным слоем поликристаллической матрицы, в результате чего основа и уток не соприкасаются. Кроме то-го , в силу малости деформаций будем считать углы ос неизменными при нагружении слоя.

Построение геометрической модели слоя тканого композита с ис-кривленными волокнами будем осуществлять при помощи платформы SALOME, которая представляет собой набор пре- и постпроцессинга, объединяет различные модули, применяемые в приложениях : -ленного моделирования в САПР до параллельных вычислений, исполь-зуется как база для проекта NURESIM (European Platform for NUclear

REactor SIMulations), предназначенного для полномасштабного моде- лирования реакторов

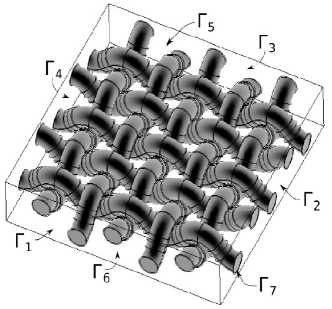
Рис. 2. Фрагмент тканого композита с искривленными волокнами

На рис. 2 представлен фрагмент слоя тканого композита с коэф-фициентами армирования ос1 = ос3 0,14 вдоль утка и основы соответ-ственно .

2.    Краевая задача

Для простоты будем предполагать, что волокна и матрица слоя модельного тканого композита изотропные, линейно упругие, не изме-няющие геометрию, взаимное расположение и тип симметрии при на-гружении . Тогда компоненты тензора напряжений о ij (r ) удовлетво-ряют уравнениям равновесия в отсутствии массовых сил ij,j (r) =0,                                    (1)

а компоненты тензора малых деформаций s ij (r) связаны с компонен-тами вектора перемещений ui (r) геометрическими соотношениями Коши ij (r)= 12 {ui,j (r)+uj,i (r)] ,                          (2)

Для описания геометрии слоя тканого композита введем единич-ную кусочно-однородную индикаторную функцию радиус-вектора r, которая принимает значение 1, если точка принадлежит нити основы или утка, и значение 0, если эта точка принадлежит матрице. Тогда о и-:

о ij (^r) = { Cij ^f klч ^r)+ Cijkl [¹ -ч ^r)]}^s kl (^r) .                (3)

В уравнениях (3) верхними индексами f и m отмечены матери-альные коэффициенты, относящиеся к волокнам и матрице соответ-ственно .

Краевая задача (1)‒(3) дополняется граничными условиями u1 (r)1г2   u1 , u3 (r)1г 1   u3 , u1 (r)1г 4   u3 (r)1г 3   u3 (r)1г 5   u2 (r)1г6   0,(4)

°12 (r)1г4 =°13 (r)1г4 =°13 (r)1г3 =°23 (r)1г3 0,

°12 (r)1г5 =°13 (r)1г5 =°12 (r)1г6 =°13 (r)1г6 0, обеспечивающими заданное макрооднородное неравнокомпонентное де-формирование в плоскости слоя, и условиями идеального сопряжения

[°ij (^r) n_j (^r    ₇       ij (^r) n_j (^rЯ1г7, [ u_i (^r)Лг₇ =[ u_i (^rИг ₇      (5)

на границах раздела фаз (рис. 2). Внутренняя пора моделируется ис-ключением из рассмотрения локального объема матрицы. Точки обра-зовавшейся внутренней поверхности Г8 не имеют ограничения на не -ремещения,                                          :

ij (^r) n j (^r )]| 8 0.                              (6)

3.    Коэффициенты концентрации напряжений

Численное решение краевой задачи (1)‒(3) с граничными уело-ВИЯМИ (4)‒(6) методом конечных элементов будем проводить в неком-мерческом пакете Code-Aster, входящем в состав платформы SALOME‒MECA. Этот пакет был разработан и сертифицирован спе-циально для французской энергетической отрасли и предназначен для задач механики сплошных сред, термо- и гидродинамики, акустики и магнетизма, выполнения расчетов для строительных конструкций и сооружений .

Дискретизация фрагмента проводилась на 16-узловые тетераэд-ральные и 20-узловые гексаэдральные изопараметрические элементы. Степень дискретизации выбиралась таким образом, чтобы полученные значения структурных перемещений, деформаций и напряжений в слое тканого композита без локальных дефектов и с несовершенствами ни качественно, ни количественно не изменялись при уменьшении харак-терных размеров конечных элементов . Этим условиям удовлетворяют сетки, содержащие 298255 и 287924 16-узловых тетраэдральных эле-ментов для композита идеальной периодической структуры и материа-ла с внутренней порой. Количество 20-узловых гексагональных эле-ментов для двух рассматриваемых случаев было одинаково и равня-лось 77760. Результаты численного решения показали, что при равнокомпонентном двухосном растяжении распределение искомых полей напряжений, деформаций и перемещений в слое материала иде-альной структуры удовлетворяет условиям симметрии и периодично-сти геометрической модели и приложенной внешней нагрузке. Это свидетельствует о корректности полученного численного решения.

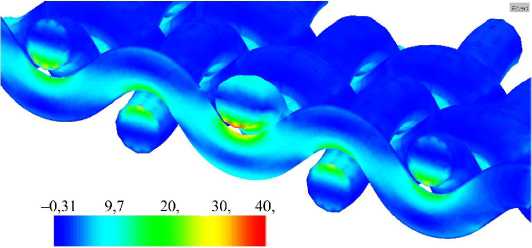
Рис. 3. Поля интенсивности напряжений фрагмента тканого композита

На рис. 3 показаны распределения интенсивностей напряжений в волокнах основы и утка при равнокомпонентном двухосном одно-родном деформировании слоя модельного тканого композита, имею-щего идеальную периодическую структуру, в собственной плоскости. Модуль Юнга и коэффициент Пуассона волокон E^f 280 ГПа и v ^f 0,20 ГПа соответствовали данным работы [3]. Упругие модули :

E^m 0,28 ГПа и v ^m 0,40.

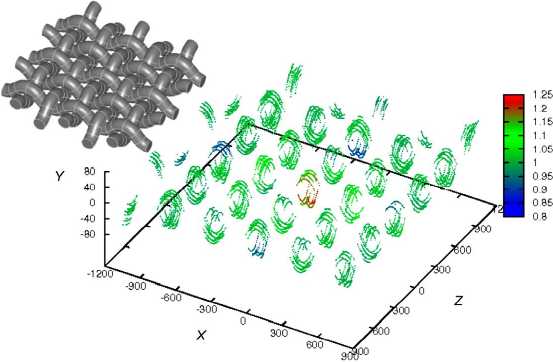
Рис. 4. Распределение коэффициентов концентрации интенсивности напряжений в слое тканого композита с локальным дефектом в виде внутренней поры

При двухосном равнокомпонентном растяжении безразмерные коэффициенты K ij ij (r)/о ipjer (r), определяемые отношением ос-редненных компонент тензора напряжений в слое модельного тканого композита с локальным дефектом и соответствующих осредненных компонент в слое материала идеальной периодической структуры, имеют следующие значения: Kо11 =1,31, Kс22 =1,93, Kа33=1,35, Kо12 =4,38, Kо13 =1,73, Kс23 =4,56. На рис. 4 показано распределе-ние локальных коэффициентов, рассчитанных как соответствующее отношение интенсивностей напряжений. Расположение областей, в ко-торых интенсивность напряжений достигает максимальных значений в местах, где искривленные волокна основы или утка имеют наиболь-шую кривизну, строго периодично. Исключение составляет область, расположенная вблизи локального дефекта, где интенсивность напря-женийв 1,25 раза превышает соответствующее значение, определенное для композита идеальной периодической структуры. Обратим внима-ние на то , что наибольший вклад в коэффициенты концентрации вно-сят касательные составляющие тензора напряжений о12 и О 23 . Значе -ния этих напряжений более чем в четыре раза превышают напряжения в идеальной периодической структуре . Поэтому для повышения спо-собности тканых композитов сопротивляться внешнему силовому воз- действию желательно предусмотреть в технологическом процессе one-рации, обеспечивающие проникновение связующего в полости техно-логических локальных дефектов, а также дополнительную пропитку связующим, доуплотнение и карбонизацию , досаждение поликристал-лической матрицы из газовой фазы в случае, если в результате ультра-звукового контроля готового изделия обнаруживаются внутренняя по-ристость. В противном случае возможно развитие дефектов и после-дующее разрушение материала матрицы по механизмам сдвигов.

Заключение

На основе построенной модели слоя тканого композита с искрив-ленными волокнами и поликристаллической матрицей определены ко-эффициенты концентрации напряжений, вызванные наличием техно-логического локального дефекта в виде закрытой поры при двухосном равнокомпонентном растяжении, определены механизмы, иниции-рующие разрушение матрицы.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант РФФИ‒Урал № 11‒01‒96033).