Концепции прогнозирования системной функциональной модели рыночной экономики с включением в нее рынка инноваций

Системная функциональная модель рыночной экономики оперирует классическими рынками факторов производства. Однако система национального воспроизводства сегодня неотделима от механизма инновационного рынка, и нововведения играют все возрастающую роль в экономическом процессе. Внедрение инноваций в любую из сторон экономической жизни общества порождает ожидание их скорой отдачи, достижения справедливого экономического эффекта, наращивания конкурентных преимуществ. В связи с этим мы считаем чрезвычайно актуальным включение в системную функциональную модель рыночной экономики механизма рынка инноваций. Под рынком инноваций мы будем подразумевать взаимодействие объема разрабатываемых и внедряемых инноваций и объема их потребления. Товар на данном рынке – не что иное, как инновации различного характера. Объектом обмена в сфере инновационной деятельности могут быть результаты любой стадии реализации инновационного процесса: фундаментальных исследований, прикладных исследований, освоения, разработки. В системной модели рыночной экономики рынок инноваций представлен количеством инновационных предприятий в качестве количественного показателя и объемом выпуска инновационной продукции в качестве стоимостного показателя.

В девятисекторную системную функциональную модель рыночной экономики включены дополнительные семь секторов: собственно рынок инноваций; влияние объема выпуска инновационной продукции на стоимость основных производственных фондов; влияние объема выпуска инновационной продукции на индекс цен; влияние объема выпуска инновационной продукции на количество занятых в экономике; влияние количества инновационных предприятий на стоимость рабочей силы; влияние количества инновационных предприятий на объем ВРП; влияние количества инновационных предприятий на ставку ссудного процента.

Модифицированная прогнозная модель рыночной экономики с учетом рынка инноваций представлена на рис. 1.

Из полученной системной функциональной модели рыночной экономики, включая рынок инноваций, мы имеем возможность сделать ряд выводов.

Рынок инноваций (10 квадрант) характеризуется низкой степенью зависимости выпуска инновационной продукции и количества инновационных предприятий.

Можно отметить, что количество инновационных предприятий в прогнозном периоде практически не влияет на объем выпуска инновационной продукции. При этом зависимость описывается степенной функцией вида:

y = 56,439x0,1802                                (1), где: у – выпуск инновационной продукции;

х – количество инновационных предприятий.

В данном случае коэффициент аппроксимации показывает достаточно низкую степень зависимости этих показателей: R² = 0,7812.

При    анализе    взаимозависимости    стоимости    основных производственных фондов и объема выпуска инновационной продукции (11 квадрант) можно отметить, что зависимость имеет устойчивый характер и описывается степенной функцией следующего вида:

y = 1E-07x1,4237                                 (2), где: у – выпуск инновационной продукции;

х – стоимость ОПФ.

В этом случае рост стоимости ОПФ вызывает устойчивый (R² = 0,9327) рост объемов выпуска инновационной продукции.

Производственная функция

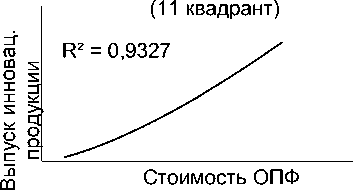
Влияние цен на выпуск инн.продукциии (12 квадрант)

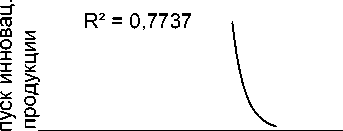
Индекс цен

Изокванты производственной функции (13 квадрант)

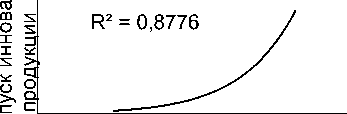
Количество занятых

Рынок инноваций (10 квадрант)

R² = 0,7812

Изокванты производственных

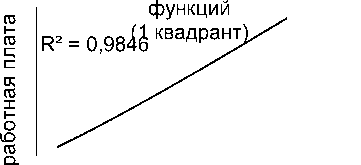
Динамика заработной платы (2 квадрант)

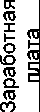
R² = 0,8553

Индекс цен

Пропорции рынка рабочей силы

(3 квадрант)

IX го

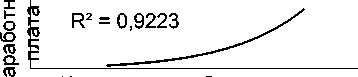
Количество рабочей силы…

Количество…

Зависимость зар.платы и

числа инновац.предприятий (квадрант 14)

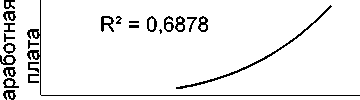
Количество инновац.…

Стоимость ОПФ

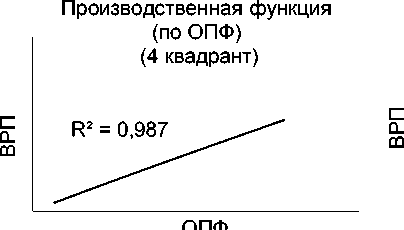
Товарный рынок (5 квадрант)

R² = 0,8474

Индекс цен

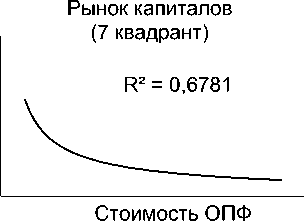
Влияние цен на стоимость капитала

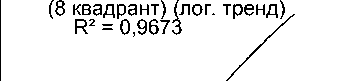
Индекс цен

Изокванты производственных

Влияние числа инновац.

функций

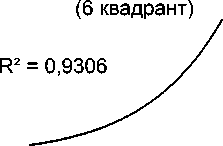
Количество занятых

Влияние стоимости

капитала на занятость рабочей сиRлы² =(09,9кв8а0д8рант) (лог. тренд)

Количество занятых

предприятий на произведенную продукцию (15 квадрант)

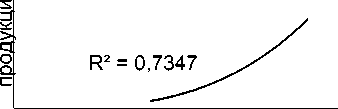
Количество инновац.…

Влияние стоимости капитала на количество инновац.

Rп²р=е0д,п6р5и4ятий (16 квадрант) (лог. тренд)

Количество инновац.…

Рис. 1 Общий вид прогнозной модели с включением рынка инноваций при использовании метода линейного прогнозирования.

Данное обстоятельство позволяет, варьируя некоторыми аспектами управления ОПФ (например, амортизационной политикой), влиять на объем выпуска инновационной продукции.

Взаимозависимость объема выпуска инновационной продукции и индекса цен (12 квадрант) имеет следующее математическое описание:

y = 342,46x-15,96                                (3), где: у – выпуск инновационной продукции;

х – индекс цен.

Данная взаимозависимость характеризуется допустимо высоким уровнем коэффициента аппроксимации R² = 0,7737. Таким образом, мы можем с большой долей вероятности утверждать, что повышение уровня индекса цен ведет к неминуемому падению объема выпуска инновационной продукции.

Подобная логика прослеживается и при анализе следующей взаимозависимости количества занятых и объема выпуска инновационной продукции (13 квадрант). При росте количества занятых в экономике увеличивается объем выпуска инновационной продукции и наоборот. Данная зависимость описывается степенной функцией вида:

y = 2E-88x27,517                              (4), где: у – выпуск инновационной продукции;

х – количество занятых.

Указанная взаимозависимость достаточно устойчива, о чем свидетельствует высокий коэффициент аппроксимации R² = 0,8776. Таким образом, можно прийти к выводу о том, что варьируя уровень занятости в экономике возможно влиять и на инновационность выпускаемой в регионе продукции.

Как и ранее, если по стоимостному показателю рынка инноваций были получены устойчивые результаты, то по количественному показателю – числу инновационных предприятий – выявлен слабый уровень зависимости введенного в модель рынка и классической системной модели.

Рассмотрим взаимовлияние количества инновационных предприятий и размера заработной платы (14 квадрант). Согласно прогнозной модели, при росте числа инновационных предприятий уровень заработной платы растет в следующей пропорции:

y = 0,0008x3,3934                             (5), где: у – заработная плата;

х – количество инновационных предприятий.

Однако, величина коэффициента аппроксимации здесь относительно невелика (R² = 0,6878), что не дает возможности выявить четкие инструменты управления в данном сочетании. Узкие возможности государственной статистики в области учета рынка инноваций не дают нам дополнительных возможностей для изыскания других инструментов, которые возможно было бы вписать в системную функциональную модель рыночной экономики с учетом рынка инноваций.

Подобная ситуация наблюдается и при исследовании взаимозависимости количества инновационных предприятий и объема производимого ВРП (15 квадрант). Выявлено, что рост числа инновационных предприятий вызывает возрастание объема производимого ВРП. В математическом виде данное явление можно представить как:

y = 0,1097x3,2295 (6), где: у – произведенная продукция;

х – количество инновационных предприятий.

Несмотря на величину коэффициента аппроксимации ниже принятого стандарта (R² = 0,7347), мы предполагаем, что данная зависимость будет укрепляться с течением времени, что позволить оформить дополнительный инструмент воздействия на состояние экономики республики.

При анализе влияния количества инновационных предприятий на норму процента (16 квадрант) было установлено, что данная взаимозависимость может быть описана логарифмической функцией следующего вида:

y = -40,39ln(x) + 206,54 (7), где: у – норма процента;

х – количество инновационных предприятий.

При этом уровень коэффициента аппроксимации значительно ниже требуемого: R² = 0,654. В связи с этим можно отметить низкий уровень зависимости указанных показателей и, как следствие, неопределенность при формировании кредитной политики региона, поскольку сокращение нормы процента вызывает неоднозначный, но вполне объяснимый рост числа инновационных предприятий.

В полученной модели был выявлен ряд ключевых взаимозависимостей, позволяющих расширить и уточнить механизм формирования экономической политики республики. Полученные нами результаты построения системной функциональной модели рыночной экономики открывают ряд инструментов для управления отдельными аспектами экономики Республики.