Кондиционирование воздуха жилых помещений с использованием аэроионизации
Автор: Варехов А.Г.
Журнал: Технико-технологические проблемы сервиса @ttps
Рубрика: Методические основы совершенствования проектирования и производства технических систем
Статья в выпуске: 1 (27), 2014 года.
Бесплатный доступ
В статье обосновывается целесообразность использования аэроионизации для кондиционирования воздуха жилых помещений. Показывается, что более широкому использованию технических средств (прежде всего, промышленных ионизаторов воздуха) препятствует недостаточная изученность условий и результатов применения этих технических средств. В статье приведены результаты точного решения задачи очистки воздуха помещений от частиц различного происхождения и различной природы при использовании ионизации воздушного объема. Определены практические параметры, в первую очередь, необходимая производительность ионного источника и время 95% - ного освобождения воздушной среды от частиц загрязнений, определяющие эффективность процесса кондиционирования.
Внутренний воздух, аэроионизация, частицы загрязнений, зарядка и дрейф частиц, время освобождения от загрязнений
Короткий адрес: https://sciup.org/148186142
IDR: 148186142 | УДК: 537.56;579.63
Текст научной статьи Кондиционирование воздуха жилых помещений с использованием аэроионизации
Постоянно возрастающий интерес к качеству атмосферного воздуха и, в особенности, воздуха замкнутых обитаемых помещений является характерной чертой сегодняшнего времени. Такие сложные состояния человека, как утомляемость, нарушение сна, раздражительность и многие другие на самом деле могут провоцироваться вполне конкретными факторами среды обитания и, прежде всего, состоянием важнейшего субстрата жизни, каким является воздух. Присутствие в воздухе опасных или неблагоприятных для жизни газообразных примесей, бактериальных клеток и вирусов, спор грибов-сапрофитов, обладающих мощными аллергенными свойствами, признается причиной примерно трети заболеваний органов дыхания. Известно, например, что в одном грамме бытовой пыли можно обнаружить 70 миллионов жизнеспособных спор грибов. Содержание наиболее опасных радионуклидов, прежде всего -222 и ℎ-222, возрастает вместе с увеличением запыленности приземных слоев атмосферного воздуха. На долю радона приходится примерно 9% летальных исходов рака дыхательных путей.
Атмосфера больших городов, в особенности, при наличии в них крупных производственных структур, способствует развитию разнообразных видов пневмокониозов с возможными осложнениями в форме туберкулеза, пневмонии, бронхиальной астмы, ревматоидного артрита и других заболеваний.
Ионизация воздуха все чаще рассматривается как наиболее эффективный метод самоочищения воздушной среды от пыли, микроорганизмов и газообразных загрязнителей различного происхождения [1-3]. Имеется достаточно широкий выбор устройств (аэроионизаторов), предназначенных для реализации метода в разных условиях. Ионизация воздуха менее эффективна с точки зрения возможности инактивации микроорганизмов, чем облучение ультрафиолетом, однако гораздо более благоприятна с точки зрения безопасности и комфорта. По этой причине аэроионы и, в особенности, легкие отрицательные (по знаку электрического заряда) ионы иногда называют «ви- таминами воздуха». Генерация в замкнутом объеме легких отрицательных ионов приводит к униполярной зарядке частиц различной природы и дрейфу этих заряженных частиц к границам объема [4,5].
Рассмотрим в общем виде задачу о зарядке и движении частиц любого происхождения и любой природы, занимающих некоторый объем газа, при ионизации этого объема. Пусть имеется сферический объем радиуса , в центре которого помещен точечный источник ионов. Этим источником, в частности, является коронирующее острие стандартного аэроионизатора. Пусть уменьшение числа частиц в единице объема (концентрации) при работающем ионизаторе и увеличение числа частиц после его выключения описываются кинетическими уравнениями первого порядка (экспонентами):
()= ⁄ ; ()= (1- ⁄ ), где , – постоянные времени. Для эффек тивного использования ионизатора, очевидно, должно выполняться неравенство ≪ ․ Ве личина легко может быть определена аналитически. Величина зависит от большого комплекса условий и может быть определена лишь экспериментально. Очевидно, что спустя некоторый промежуток времени работы ионизатора устанавливается квазистационар-ный уровень концентрации, определяемый при = равенством:
( )( )
.
При условии ≪ получаем
≅
Стационарные концентрации при этом равны:
( )= ( )≅ ⁄
Постоянную времени можно определить следующим образом. При средней скорости дрейфа заряженных частиц к «стенке» сферического объема, равной ̅̅̅, уменьшение концентрации частиц в единицу времени выражается соотношением откуда после интегрирования следует ()= ( ̅̅̅̅⁄ ) .
Таким образом, получаем соотношение
= ⁄3̅̅̅. Величина времени дрейфа частиц от источника ионов до «стенки» = ⁄̅̅̅ может рассматриваться как основной параметр, характеризующий эффективность ионизатора. За время = =3 , определяемое как время освобождения воздушного объема от загрязнений, концентрация частиц уменьшается до значения ( ) ≅0,05 . Значение ( ) может, вообще говоря, оказаться выше значения
( ). Будем считать, что неравенство ≪ выполняется настолько сильно, что > , и потому для оценки квазистационарного уровня концентрации примем значение ( )≅
0,05 . Во всяком случае, это позволяет избе жать трудностей в определении и, следовательно, . Определим теперь величину для рассматриваемого сферического объема радиуса .
В объеме находятся частицы с весовой концентрацией , счетной концентрацией и функцией плотности вероятности распределения по размерам () ( - радиус частицы). Ток в цепи источника ионов равен , заряд генерируемых ионов равен ; тогда производительность источника или число ионов, продуцируемых в единицу времени, равен = ⁄ . По тенциал ионного источника принимается равным относительно «стенки» сферического объема, потенциал которой принимается равным нулю. При включении в момент времени =0 разности потенциалов , большей значения, соответствующего порогу зажигания разряда, практически мгновенно (вследствие большой подвижности ионов) устанавливается равновесная концентрация ионов. Далее имеет место зарядка частиц и дрейф их к «стенке» объема. Дрейф частиц происходит как под действием поля, обусловленного разностью потенциалов , так и вследствие градиента собственного униполярного объемного заряда частиц и ионов.
В дальнейшем, принимаются следующие допущения и упрощения: физические константы ионов (заряд и подвижность) не меняются со временем; частицы дисперсной фазы монодисперсны и представляют собой сферы радиуса ; седиментация (гравитационное осаждение) не искажает сферической симметрии задачи, что справедливо для малых частиц; «запирание» коронного тока генерируемым объемным зарядом отсутствует вследствие малости концентрации частиц; эффективность «прилипания» частиц к «стенке» принимается равной единице; движение частиц происходит без их агрегации, то есть независимо друг от друга. В последующих расчетах приняты следующие значения: = 1мкм; =0,1мг∙ м ; =1м ; = =1,6∙10 Кл;
=10 Α; = 30кВ. Кинетика зарядки частиц описывается выражением [6]
=4 (1+2 ) + и V £+2/ Р 4п£0+пепк^
( ), где: -диэлектрическая постоянная частицы;
=8,854∙10 Ф∙м -электрическая постоянная; - напряженность поля; - концентрация ионов; -подвижность ионов;
-постоянная Больцмана; -абсолютная температура; ( )- безразмерная функция диффузионной зарядки, определяемая графиком рис. 1. Величина пt откладывается по горизонтальной оси в единицах (млрд. с • см- 3). В этом выражении первое слагаемое описывает так называемую ударную, достаточно быструю зарядку частиц, причем поле Ер действует в непосредственной близости от поверхности частицы, где напряженность поля может быть очень велика. Второе слагаемое описывает относительно медленную диффузионную зарядку, действующую во всем объеме, занятом частицами. Соотношение обоих кинетических слагаемых определяется концентрацией ионов, то есть производительностью ионного источника. Более точно диффузионная зарядка исследована в работе Кирша и Загнитько [7].
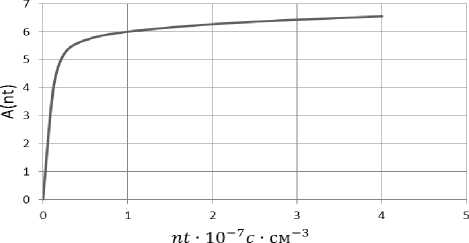
Рисунок 1. Безразмерная функция диффузионной зарядки
Отметим, что даже при незначительном по величине коронном токе i = 10“ 6А = 1мкА ионизатор производит =10 ⁄1.6∙10 ≅
6 • 1012 однозарядных легких ионов в секунду. Это означает, что так называемая фоновая концентрация таких ионов, характерная для открытой атмосферы и равная п = 100см_3, достигается в заданном сферическом объеме за время, равное примерно 10 “ 4 секунды.
Скорость дрейфа заряжающихся частиц определяется соотношением
Q (R,t)E(R) = 6RHT v d, в левой части которого находится электрическая (пондеромоторная) сила, действующая на частицу, а в правой - механическая сила сопротивления среды движению частицы; п — динамическая вязкость среды; кроме того, п = pv (v - кинематическая вязкость; р — плотность воздуха). Достаточным условием применимости этого соотношения является, как известно, малость числа Рейнольдса для частицы, то есть Re = 2r pvd/p « 1.
Таким образом, скорость дрейфа получаем в виде
= ^(7^?) = Q (R ,tMR)B , где B = 1/6rtt] - механическая подвижность частицы.
Примем в качестве параметра, характеризующего осадительные возможности приня- той модели, время дрейфа частицы от источника ионов до «стенки». Напряженность поля ( ) представим в виде суммы
Е (R) = Е1(й) + Е2(Ю, где: Е( (R) — напряженность электростатического поля, обусловленная приложенной разностью потенциалов; ( ) - напряженность поля, обусловленного объемным зарядом ионов в сфере радиуса R, из которой удалены частицы.
Напряженность поля E((_R") определяется соот- ношением
Е1 (Ю = Ео^ , где: Ео — напряженность поля у коронирующе- го острия; — радиус кривизны коронирую-щего острия. Из граничных условий, кроме то- го, имеем
U = ^°Е1(Л) dR , откуда после элементарного интегрирования получаем равенство = , после чего за пишем
Е 1 (Ю = U^ .
Напряженность поля ( ) найдем из выражения (теорема Гаусса):
#ЁТ2 •dS = 1£qь откуда получим сразу
Е2 (R) • 4rR2 = - Гй 4r# 2p(^)dK, So rO где: p(^) — объемная плотность заряда ионов; ^ - текущее значение переменной интегриро- вания.
Внешняя область короны является областью дрейфа униполярных ионов, плотность тока которых j = ^enk ^Е1(Д) + Е2(Д)], откуда объемная плотность заряда ионов
J 4nR2kt [E1(R)+E2(R)] .
Используя теперь выражение для слагаемого ( ) , получаем выражение для объем- ной плотности в виде:
() ∙
Р( ) к i [4RUr0 + 4RR2E2(Д)]
После интегрирования для составляю- щей напряженности ( ) получаем:
()= ∙ ℛ ℛ
∫ ℛ (ℛ)
Последнее выражение дает возмож- ность, используя методы численного интегрирования, получить приближенный вид функции, описывающей компоненту напряженности поля ( ). Для этого, начиная от точки = , где ( = ) = 0 , необходимо было зада ваться последовательными малыми интервалами AR и, считая на каждом из таких интервалов функцию ( ) линейной, определять такие значения ( ), которые удовлетворяли бы полученному интегральному соотношению. Результаты таких расчетов для слагаемого напряженности поля ( ) представлены на рис.2, где напряженности поля выражены в единицах кВ∙м . Нижняя граница расстояния напряженность поля
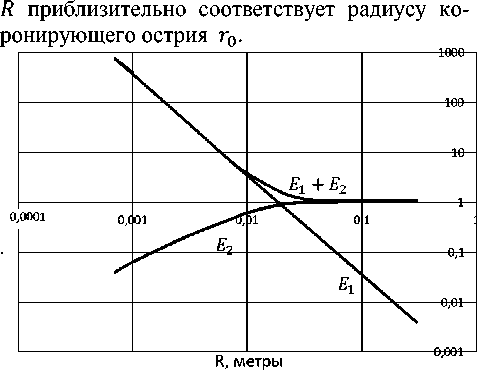
Рисунок 2. Расчетные напряженности поля ( ), ( ) и сумма ( )+ ( ).
В этих расчетах использовались значения =10 м и = 2,1м ∙В ∙с .
На этом же рисунке представлены зависимости слагаемого ( ) и суммы
()+ ( ).
Из рис.2 следует, что ( ) весьма быстро убывает и уже при значениях, больших = 2см, напряженность поля почти полностью определяется компонентой ( ). Так называемая ударная зарядка частиц, описываемая первым слагаемым в исходном полном уравнении кинетики зарядки, имеет место в небольшом (радиусом 1-2 мм) объеме вблизи коронирующего острия. В этом объеме скорости зарядки и дрейфа велики, однако влияние этой области вследствие ее малости в дальнейшем учитываться не будет. Таким образом, практически во всем объеме при напряженности поля ( )≅ ( )≤1000В∙м будет иметь место диффузионная зарядка частиц, определяемая вторым слагаемым в уравнении кинетики. Напряженность поля ( ) можно было бы аппроксимировать каким-либо подходящим выражением, однако это сильно усложнило бы аналитическое решение. На основании рис.2 с удовлетворительной точностью можно принять усредненное значение по всему объему ( )= ср. С учетом условия ( )≫ ( ) при >10 м выражение для объемной плотности ионов запишется тогда в виде
()= ∙ .
4nR2kiEro где отсчитывается теперь от некоторого значения , соответствующего условию ( )≫
( ).
Возвращаясь к выражению для скорости дрейфа, теперь можно записать
= = ( , ) ср .
Численные расчеты величины (рис.1) на основании уравнения для плотности ионов показывают, что необходимо использовать начальный участок зависимости ( ), который может быть аппроксимирован линейной зависимостью ( )= где λ - коэффи циент пропорциональности.
Решение запишется следующим образом:
ℛ = 4 λ .
(ℛ) ср
Подстановка выражения для ср при учете равенства ( )= ( ) после интегри рования позволяет записать решение следующим образом:
( )= , откуда, в частности, следует, что несколько произвольный выбор величины радиуса ма ло сказывается на результате вследствие того, что ≪ . Поэтому окончательно получаем
= .
Коэффициент пропорциональности λ может быть определен по графику рис.1 из значения производной ´( )| . Таким об разом, получаем значение =4∙10 м ∙с . При вышеприведенных значениях величин, входящих в последнюю формулу, подсчет дает для времени освобождения от частиц загрязнений значение, равное =0,92∙10с≅
153мин. Это значение достаточно хорошо согласуется с типичными экспериментально полученными величинами.
При дрейфе частиц от центра к «стенке» объема возникает, вообще говоря, диффузионный поток частиц обратного направления, обусловленный наличием градиента концентрации. Однако при условии равенства дрейфового и диффузионного потоков ср ( , )=
. 8R
Численный расчет показывает, что при принятом значении весовой концентрации частиц =0,1мг∙м ( =10м ) необходимые значения | |= ⁄ намного больше тех, которые в действительности имеют место.
Подсчет величины t имеет большое значение для расчета и проектирования устройств, использующих ионизацию газовой среды для освобождения ее от коллоидных примесей. Точное решение задачи, в первую очередь, путем введения функции распределения по размерам частиц, а также детального анализа поля в рассматриваемой области, со- пряжено с большими трудностями. Однако в практических случаях соизмеримость или даже достаточно близкое соответствие теоретических и экспериментальных результатов позволяют надеяться на практическое применение этих результатов. Например, при использовании в качестве преципитатора [8] стандартного аэроионизатора АИР-2 в стеклянном боксе объемом 0,2 м3 с взвесью культуры Staphylococcus aureus, приготовленной на стерильной водопроводной воде, плотностью 200млн. бактериальных тел в 1мл, напряжение на излучателе ионов составляло 3,5кВ, размер взвешенных частиц – в пределах от 5 до 50мкм. Полное освобождение от взвеси в боксе происходило по истечении 60-90 минут. В другом случае [9] при использовании генератора отрицательных ионов при напряжении 75кВ и токе 0,5мА, то есть гораздо больших, чем в наших расчетах, при плотности ионов около 5 • 105см ”3 и на расстоянии 1,5 метра от генератора было отмечено уменьшение числа колоний на чашках Петри от 150 до 1-10 в течение времени от 13 до 38 минут; в другой серии экспериментов в той же работе и в тех же условиях – за время от 18 до 78 минут, причем все данные опытов были тщательно статистически обработаны.
Существует множество старых и новых данных, свидетельствующих о том, что жизнеспособность бактерий и вирусов в форме биологически активной пыли сохраняется в течение промежутков времени от нескольких часов до нескольких месяцев. Например, гемолитический стрептококк выживает в пыли около 10 недель, дифтерийная палочка, выдержанная в вакууме, способна сохранять жизнеспособность до 4 лет; на поверхности дерева - 3-5 месяцев, на никелированных поверхностях – 9 дней, на поверхности конструкционных сталей – около одного часа. Вирус гриппа на оконном стекле живет в течение 1 – 5 суток. Таких примеров множество и все они свидетельствуют о том, что латентная патогенность многих форм представляет собой постоянно действующую угрозу. Интерес к оздоравливающему и лечебному действию аэроионизации со времени деятельности А.Л.Чижевского, который первым в новейшем времени осознал важность и полезность метода, периодически то угасал, то возбуждался. Эта неоднозначность и раньше, и сейчас во многом была связана с отсутствием, с одной стороны, сколько-нибудь надежного теоретического подхода к этой проблеме, а, с другой стороны, с пониманием тесной связанности качества воздуха и сложных физиологических состояний человеческого организма. Так, например, система кондиционирования воздуха всемирно известного крытого нью-йоркского стадиона «Madison Square Garden» на 22 тысячи зрителей, диаметр которого равен 127,5 метров, а высота – 27 метров, была снабжена ионизатором разработки компании Cosa-Tron, лидирующей на рынке устройств, предназначенных для повышения качества воздуха. В используемой системе действовали совместно статическое и высокочастотное электрические поля. Хотя в этом, как и в других подобных случаях, отмечалось благоприятное общее действие ионизации воздушной среды в условиях замкнутых жилых помещений и на очень плотные массы людей в общественных зданиях и сооружениях, механизм такого действия во многом остается неизученным.


