Конечно-элементная модель процесса глубокой вытяжки осесимметричных деталей

A finite element modelling program has been formulated to simulate the axisymmetric deep cup drawing process. Pinite element program is based on the upper bound, techniques.

The sheet material was assumed to obey Hillis anisotropic yield criterion and its associated flow rule. Workpiece response is incompressible. The work hardening characteristics of the material and Coulomb friction between the sheet metal and. forming tools were Incorporated into the simulations. Special algorithms for dealing with contact conditiom (Coulomb friction) and finite strain have been developed.

Computed results of analysis were compared with experiaen-tal results and good agreement was obtained. Good correlation was found for load-displacement curves and deformed configurations of the workpiece during the deformation. Although the program is unoptimixed initial CPU times suggest that program is suitable for large-scale industrial forming simulations.

Среди технологических операций, применяемых в машиностргс-нии, наиболее экономичной является листовая штамповка. Вместе с тем она характеризуется значительной предварительной подготовкой производства, что приводит к существенным трудностям, особенно в серийном и мелкосерийном производстве. В связи с этим разработка модели, позволяющей получать достаточно полную информацию о параметрах процесса, представляется актуальной задачей.

Формоизменение в процессе листовой штамповки имеет ряд особенностей. К числу наиболее сущесчвенных следует отнести геометрическую нелинейность (значительные перемещения и градиенты перемещений), наличие деформационной анизротропии и упрочнение материала, а также неоднородность деформаций по сечению заготовки. Отмеченные выше особенности, наряду с нестационарностью процесса, создают значительные трудности при построении математической модели.

Существующие в настоящее время модели листовой штамповки условно можно разделить на два типа. К первому следует отнести модели интегрального типа, использующие весьма грубые гипотезы, но позволяющие аналитически оценить общие характеристики процесса (например, усилие, ряд геометрических параметров). Модели второго типа предполагают решение задачи каким-либо численным методом в объемной постановке. В этом случае исследователь имеет возможность получить максимум информации, однако реализация на ПЭВМ подобных моделей приводит к трудно разрешимым

Конечно-элементная модель проблемам. Предлагаемая в настоященй статье модель занимает промежуточное положение. Она позволяет получить достаточно полную информацию о процессе и в то «е время не требует высоких вычислительных характеристик ПЭВМ.

В качестве исходной основы для математической модели выбрано неравенство верхней оценки, являющееся следствием известного постулата Друккера и уравнения баланса мощностей [2]:

р' • f' dV - J Т* -и' dS + J Т^ ■ у' dS > J T-v*dS + J T- v*dS. (1 )

V             s            s             s           s

T             S              v            S

Значками ..... , " * " обозначаются переменные, имеющие смысл возможных и заданных соответственно. Остальные символы имеют следующее содержание: у - объем рассматриваемой области трехмерного пространства; 8т>Зу - части границы д, на которых зада ны поверхностные усилия и скорости соответственно; g - поверх-S ность контакта с подвижным инструментом; cr, f - тензоры напряжений Коши и деформации скорости соответственно; v - поле вектора скоростей перемещений. Индексом т - отмечены касательные составляющие соответствующей переменной. Под кинематически возможным полем скоростей у' понимаем поле, которое удовлетворяет условию несжимаемости в объеме V, кинематическим граничным условиям на S_ и g и, кроме того, имеет необходимую степень дифференцируемости по всем пространственным пе-; сменным. Обозначим множество кинематически допустимых скоростей через К- Если правую часть неравенства (,) определить как «7 , а левую, являющуюся выпуклым нелинейным Функционалом над К, как J, то неравенство (1) запишется следующим образом:

J (V* ) > J

V у'еК,

V t€[0. +<ю).

Таким образом, значение мощности действительных поверхностных сил на границе, где заданы скорости перемещений, ограничены сверху величиной in/ J(7/ ), поэтому несложно получить оценку сверху на значение поверхностных усилий на границах g ид.

_ V S

Первое слагаемое J(t>' ), являющееся мощностью пластического деФормирования, для случая трансверсально-анизотропного, жесткопластического материала может быть записано:

№ = Г oD’ ЗУ. о

где о s

текущее значение предела пластичности, измеренного в плоскости листа, a D^,-- эффективная интенсивность тензора де-Формаиич скорости:

Z_jjaZ" f у' 1+2к X

^1 ⁾ ^^2 ^{? + &}^Э ^{} + 2}^1 ^.2 *

+ 2(1+2к)   ^2 ? д^

а

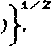
где Jz - отношение величин деформаций в направлениях, связанных с главными осями анизотропии; р.д - коэффициенты анизотропии, зависящие от пределов текучести в различных направлениях [1].

Для получения поля скоростей перемещений цеК, обеспечивающего достижение {п/ Jfv), как правило, прибегают к непосредственному построению кинематически возможного поля [2]. Отмеченный подход, по нашему мнению, малоперспективен по ряду причин. Во-первых, непосредственное построение поля перемещений зачастую отражает не реальный процесс деформирования, а представление исследователя об этом процессе. Во-вторых, в процессах с большими деформациями процедуру построения поля скоростей необходимо повторять практически каждый раз, как только осуществляется переход от одной конфигурации к другой. И наконец, серьезные проблемы возникают в случае моделирования деформирования материала с упрочнением. Упомянутые выше сложности легко обойти, если обратиться к методу конечных элементов. В этом случае к заменяется конечномерным подпространством К с. К, nsN, причем V у е К, можно построить последовательность v «К , что и -» 5 е К- В частности, в методе конечных элементов К образуется как пространство, натянутое на систему базисных функций N (х) (Функции Формы). Непосредственное применение МКЭ к (1) приводит к системе нелинейных уравнений. Линеаризация достигается использованием неравенства Коши-Буняковского к первому слагаемому в J(v). В этом случае получаем Функционал :

Jt(v)

S%dV ■ JciT )²dV + (J T*v'ds/+2 (5)

V        V            s             s

T              s

Заметим, что неравенство (2) сохранится и для квадратов величин Функционалов только в случае, когда J > О, V у е К- Последнее условие в общем случае не выполняется и поэтому требует предварительной проверки для каждой конкретной задачи.

Записав для (5) в качестве необходимых условий уравнения Эйлера, можно получить систему линейных алгебраических уравнении. Условие несжимаемости материала реализуется введением в (5) функции штрафа pj(div и) du, где р - подходящее

Конечно-элементная модель большое положительное число.

Алгоритм решения задачи состоит в последовательном построении глобальной матрицы жесткости, решении системы алгебраических уравнений, определении скоростей перемещений и новой конфигурации области, уточнении механических свойств и граничных условий. Для реализации условия обтекания предложена процедура вычеркивания связанных величин, позволяющая сохранять симметричную структуру матрицы.

Разработанная конечно-элементная модель тестировалась на некоторых известных задачах. Одна из них - задача осадки цилиндра в случае отсутствия трения на контактных поверхностях. Деформация в таком варианте является однородной и верхняя оценка на величину усилия совпадает с точным решением, приведенным в [21- Расчеты проводились для следующих исходных данных: диаметр цилиндра бОмм, высота >5мм, h=1, Р/М-1/3, скорость осадки

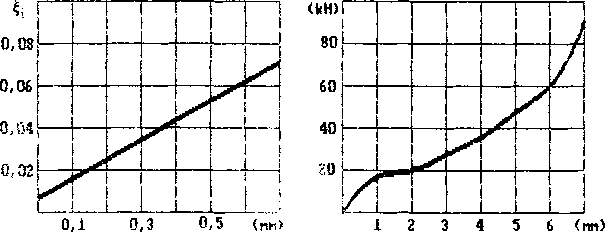
Рис.1 Интенсивность деформации скорости от хода пзансона.

пуансона.

Рис.2 Усилие осадки от хода

) мм/с, о1 = 140 " Н °Л11 кг/нм2, где к - интенсивность тензора деформации Генки. На рис. J приведено изменение интенсивности деформации скорости D в зависимости от хода пуансона. Значение s

Л в точности совпадает с аналитическим: л =У/Н, где И - теку-s                                             s щее значение высоты цилиндра £21. На рис.2 представлен график зависимости усилия от хода верхней плиты при отсутствии сил трения по поверхности контакта. Решение совпадает с аналитическим £2J.Заметим, что при наложении условия трения на контактных поверхностях в начальный момент осадки CAZ ~ 1 мм> возникает явление двойного бочкообразования цилиндра <рис.з>. При последующем деформировании "двойная бочка" переходит в одинарную. Подобное течение процесса соответствует результатам эксперимента, описанным в [2].

Помимо задачи осадки, для тестирования модели использовались экспериментальные данные по процессу глубокой вытяжки сФе-

В.Д Ониокив, А,А Ферягич рическим пуансоном аустенитного стэичьного листа, приведенные в [5]. Использовались следующие данные для расчетов: диаметр заготовки 166 мм, толщина О,В4 мм, радиус пуансона 37,5 мм, >._1, 7/М-1/3, закон упрочнения а ^2Д4 * 135,3 к0,411 МПа, усилие

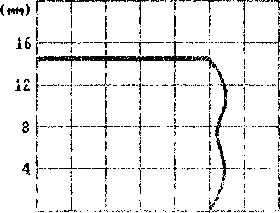
31.34   31.50   31.66 Я (мм)

Рш .З Двойное "бочкообразование" на боковой поверхности цилиндра.

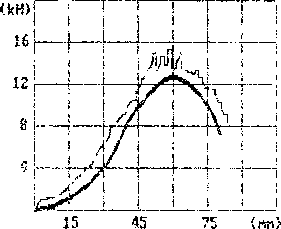
Рис .4 Усилие итамповки от хода пзансона(””-■ эксп.;— - расчет)

прижима 99,ОЬ КН, скорость движения пуансона 0,033 мм/с, коэффициент трения 0,15. На рю.4 представлены графики результатов экспериментов и расчетов по определению усилия вытяжки. Кривая расчетных данных отличается не более чем на 20% от эксперимен-

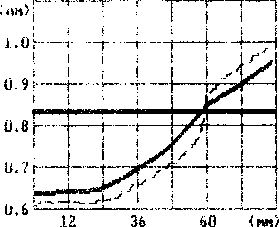
Рис.З Утонение в зависииости от радиальной координаты (—»-эксп.;-- -расч.).

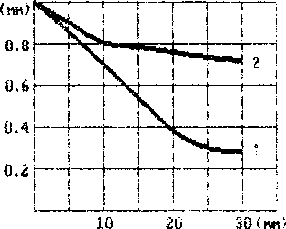
Рис. 6 Утешение в зависимости от хода пэансона( 1-идеал.сназка; 2-прм наличии трения).

тальных данных. Для сравнения локальных характеристик процесса на рис.р приведены экспериментальные и расчетные данные изменения толщины стенки при ходе пуансона 75 мм. Здесь также имеет

Конечно-элементная модель место удовлетворительное совпадение. Это позволяет сделать вывод об адекватности разработанной модели технологическому процессу.

Предложенная модель использовалась для анализа влияния параметров материала и процесса на основные характеристики деформирования. При этом использовались следующие данные: диаметр заготовки 40 мм, толщина листа 1 мм, h=1,5, ¥/М=1/3> а = 40+17>6 х ft^0,33 кг/мм². В ходе расчетов осуществлялся визуальный контроль за геометрией деформируемой области, которая отображалась на экране дисплея, на каждом временном шаге. Отметим, что практически в течение всего процесса деформирования, за исключением самых первых моментов, отсутствует контакт между нижней поверхностью пуансона и металлом. Описанный эффект, по-видимому, является следствием действия изгибных напряжений. Результаты расчета величины утонения листа приведены на рис. б- При данных условиях наибольшая величина утонения на начальных этапах отмечается вблизи радиусного участка пуансона. В дальнейшем максимум утонения перемещается в днище. Это объясняется перетеканием металла на боковую поверхность, главным образом, за счет донной части заготовки, а не Фланца, где существуют зоны стесненного деформирования. Таким образом, часто используемая в аналитических расчетах гипотеза о движении днища как единого целого (4) имеет ограниченные рамки применения. Анал/ ? результатов также показывает, что наиболее существенное влияние на величину утонения и усилия штамповки оказывает трение.

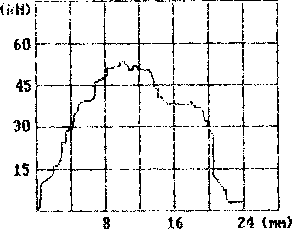
Рис .7 Зависимость зомиг or хода изамсоя»,

На рис. 7 приведен график усилия штамповки в ходе процесса деформирования для описанных выше исходных данных. Изломы в графике этой функции связаны с пространственной дискретизацией области, что приводит к "порционному" изменению поверхности

В.Д Онискив, АА Ферягин контакта. Особенно заметен этот эффект, когда элемент попадает на поверхность, где заданы условия трения. Максимум усилия штамповки соответствует 4700 кг. СЬгласно [3] максимальное усилие составляет 4000 кг. В предположении отсутствия трения по контактным поверхностям, максимальное значение усилия соответствует 3200 кг.

В заключение отметим, что предложенная модель позволяет решать задачи рационального выбора параметров процесса, а направление дальнейших исследований связано с анализом возможности возникновения пластической неустойчивости процесса деформирования.