Конечно-элементная модель расчета величины накопленной деформации в процессе горячей раскатки колец

формированное состояние и величину степени накопленной деформации.

При разработке конечно-элементной модели учтено, что, благодаря симметрии, структура и свойства раскатанного кольца идентичны для всех сечений по окружности. Учитывая это обстоятельство, модель была построена не для всего кольца, а для сегмента, равного 6-ти длинам очага деформации. Сегмент разбивается на треугольные конечные элементы, как показано на рис. 2.

Угол ф , определяющий положение элемента в области решения, находим по следующей формуле [2].

ф =

12 • L • R, (2 R h + 2 R b )

где R H , R B — наружный и внутренний радиусы кольца;

Ri – средний радиус кольца в i обороте.

L – длинна дуги контакта с любым из валков.

Для её определения применена формула [2]

L = V R 1(2) ^А h ,              (2)

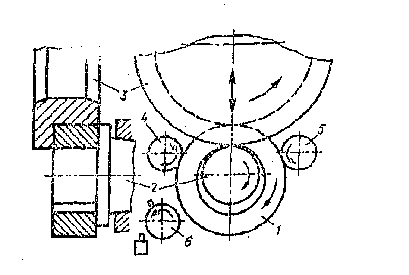
Рис. 1. Схема процесса горячей раскатки колец: 1 – заготовка, 2 –внутренний неприводной валок (дорн), 3 – внешний приводной валок, 4, 5 – направляющие ролики, 6 – конечный выключатель (контроль диаметра)

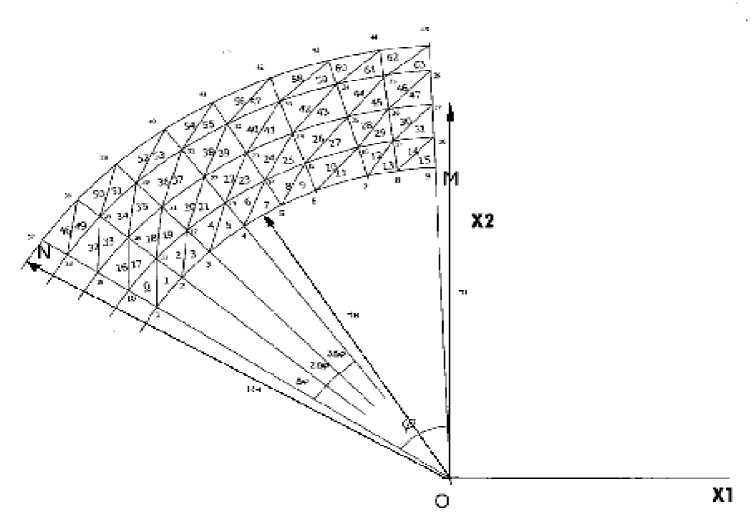
Рис. 2 Разбиение области решения на конечные элементы

где R ₁ , R ₂ – радиусы приводного и не приводного валков

A h - абсолютное обжатие

Предварительно разбиваем область решения на четырехугольные секторы, каждый из которых соответствует двум соседним треугольным элементам. Имеется N рядов секторов по радиальному направлению и M – в тангенциальном направлении. Имеется 2 • N • M треугольных элементов и ( M + 1) • ( N + 1) узлов. Нумерация узлов показана на рис. 2. Координаты i-го узла по осям 1 и 2 обозначим как x_{i 1} , x_{i 2} :

x i 1

^DBH + ^DH D BH

2     2 • N

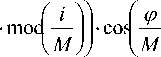
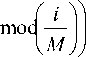
;(3)

x i 2

D BH + ^DH D BH

2     2 • N

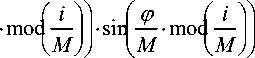
. (4)

В процессе расчета координаты узлов в любой точке области расчета будут меняться на пе- ремещения узлов di1 , di2 . Для нахождения di1 , di2 воспользуемся энергетическим методом [3]. Рассмотрим отдельный треугольный элемент i с узлами 1, 2, 3 на рис 3.

Предположим, что элемент вначале не напряжен, уз л овые силы равны 0. Затем силы f ₁ , f ₂ , f ₃ прикладываются к соответствующим узлам элемента. Новая конфигурация узлов будет иметь смещение d — d i 1 , d 1 ₂, d 22 1 , d 22 , d 3 1 , d ₃ ⁱ ₂ . Верхний индекс относится к элементу, в дальнейшем его опускаем. Первый нижний индекс относится к узлу, а второй – к координате. Потенциальная энергия I новой конфигурации по отношению к исходной представляет собой разницу между энергией напряженного состояния, накопленной в элементе U и работой W, совершенной силами f ₁ , f ₂ , f ₃ на векторе перемещений d, [3].

I — U W — [( o il s 'll + ^ 22 ^ 22 + ² ° 12 ^£ '12 ) d ^v f ,1 ^d 11

²                                         , (5)

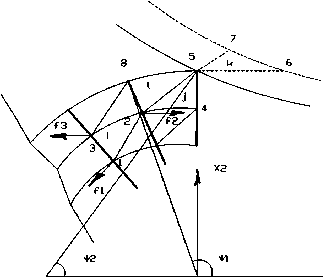
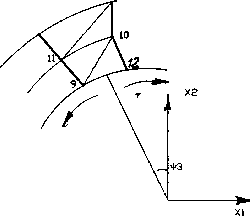
Рис 3. Задание граничных условий в задаче о деформировании сегмента где d12 ……. d32 – перемещения в узлах элемента по направлениям 1,2 соответственно;

f ₁₁ …… f ₃₂ – силы, под действием которых происходит смещение узлов в направлении 1,2 соответственно;

е11, е22 – нормальные, а е12 – касательный компоненты тензора деформации;

у11у22 – нормальные, у12 – касательный компоненты тензора напряжений.

Интегрирование проводится по объему dV (в рассматриваемом случае плоской деформации – по площади элемента dF). Для удобства дальнейшего решения представим уравнение (5) в матричной форме.

яний можно найти в [3]. Здесь приведены его значения, причем только для плоской деформации и энергетического подхода.

Упругая деформация:

c = D - e,

D =

E

1 + v

1 - v

1 - 2 v v

1 - 2 v 0

v

1 - 2 v

1 - v

1 - 2 v

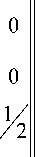
I = 2 J ст^т - e-dF - d ^T - f = 2 J e^T^ D e dF - d ^T f = = 1 d ^T (fl И -I D ll-I BdF d - d ^T f

Значения компонент вектора d = dd 11 ■ •• d ₃₂ должны быть такими, чтобы потенциальная энергия I имела минимальное значение:

Пластическое состояние:

d c =( D ' ||-|| D ' | I)- d e = | D - d e , (12) где D ^e – для упругой части деформации,

D ^p – для пластической части деформации.

5 I   n

----= 0 ; i=1_3, j=1_2 .

,

После дифференцирования, в векторной форме получим:

(JIBIT-I Dll-IBII •dF )•d=f. (8)

Чтобы понять обозначения, B , и D еще раз рассмотрим отдельный элемент, представленный на рис.3.

Если он треугольный как в нашем случае, и напряжения в нем меняются линейно, то в [3] рекомендуется связывать значения перемещения узлов элемента и его деформацию следующей формулой.

De = 2 G	1 - v     v
	1 - 2 v 1 - 2 v v     1 - v
	1 - 2 v 1 - 2 v 00

e =

^e ii ^e 22 ^e i2

2 А

x 22   x 32

^X 3 1 - x 21

^X 3 1 x 21 x 22 - x 32

x 32 x 12

x 1 1 - ^X 3 1

^x 11   ^x 31

x 12 x 22 0

x 32 - ^x 12

x 21 - x 11 x 12 - x 22

X

d 11

d 12

^d 21

^d 22

^d 31

^d 32

В матричной форме выражение (9) запишем следующим образом:

e = I B U - d .             (9 а)

Как видно из (9) B выражает изменения координат узлов треугольного элемента при со-

хранении его площади и связывает перемещение в его узлах с накопленной деформацией.

В свою очередь D выражает связь между тензором деформации и тензором напряжений. Его значения различны для упругого и пластического состояния. Вывод D для обоих состо-

Dp

' '

' '

' '

2 G S

c 11	C 11	C 11	C 22 f	C 11	C
C 22	C 11 "	C 22	C 22	C 22	c
C 12	C 11	C 12	C 22	C 12	c

, (14)

12 '

12 '

где модуль сдвига

G =

E

2(1 + v ) ;

S – характеристический параметр упруго-пластического состояния

5 = 3 c

1 + ^s-

3G

V 7

Данный параметр позволяет учесть зависимости напряжений от деформации и других параметров процесса, которые выражены через соотношение вида cs = cs (e, e, Т ,cSo, а, в, с),        (17)

где e -накопленная деформация при одноосном сжатии (растяжении);

• e - скорость деформации;

• Т – температура;

c _so а,в,с - эмпирически определяемые соотношения. Поиску таких соотношений посвяще-

но большое количество исследований. Нами использованы результаты [4] для сплавов, используемых при раскатки колец ГТД.

Вернемся к формуле (8), которая, как теперь понятно, выражает связь между усилием в элементе, с одной стороны, и напряжением, деформацией и перемещением – с другой. Исключив из формулы (8) перемещения, обозначим её левую часть следующим образом.

II Ц =)l N f-I И -I I N • dF . (18)

K – это матрица жесткости. В ней учтены все параметры деформации, приведенные выше. Если данная матрица приведена для одного треугольного элемента – она называется локальной. Глобальная матрица будет представлять собой матрицу правой части системы ( M +1 )( N +1 ) уравнений, формируемую как алгебраическая сумма локальных матриц каждого элемента.

II K I- d = f . (19)

Надо отметить, что нам уже известно напряжение a s на первом шаге из свойств материала, а на следующих шагах – из формулы (12). Система (19) с нулевым вектором f имеет бесконечное множество решений, соответствующих движению объекта моделирования как жесткого тела. Для получения решения, описывающего движение реально деформируемого тела, необходимо задать граничные условия. С вычислительной точки зрения, положение граничных условий состоит в построении вектора правых частей уравнения (19). С физической точки зрения – в учете контактного взаимодействия заготовки с приводным и неприводным валками. Для уравнений, описывающих узлы на свободных поверхностях заготовки, свободный член равен 0. Рассмотрим различные подходы к построению граничных условий на приводном и неприводном валке.

Для неприводного валка в первой половине дуги захвата силы направлены против направления движения металла, во второй – по направлению движения (рис. 3, б). Для каждого узла в контакте с валком направление действия сил известно. P - нормальное давление, т = ц Р -сила трения, ц - коэффициент трения.

Рассмотрим уравнение (19), которое в развернутом виде для узла 9 запишется следующим образом (рис. 3,б).

⁺ k 17,20 d 102 ⁺

k 17,17 d 91 ⁺ k 17,18 d 92 ⁺ k 17,19 d 101 ⁺ k 17,21 d 111 ⁺ k 17,22 d 112 = f 11 =

= цР cos ф 3 - P sin ф 3 ,

k 18,17 d 91 ⁺ k 18,18 d 92 ⁺ k 18,19 d 101 ⁺ k 18,20 d 102 ⁺

⁺ k 18,21 d 111 ⁺ k 18,22 d 112 = ^f 92 =

= P sin ф 3 + ц Р cos ф 3 .                (21)

При решении уравнений (20) методом Гаусса, учтем условие непроникновения материала заготовки в неприводной валок:

d ₉₁ • sin ф ₃ = d ₉₂ • cos ф ₃ .        (22)

Это условие позволит исключить из системы уравнений (19) d ₉₂ Данноепреобразование проделываем для всех уравнений, содержащих узлы, лежащие на поверхности неприводного валка.

На приводном валке известна скорость вращения, но неизвестно взаимное смещение поверхностей металла и валка. Применим следующий прием [3] .

Введем фиктивный слой элементов. Покажем его на примере элемента, с узлами 7, 6 (рис 3а). Эти узлы движутся как жестко связанные с валком. Узлы контактного слоя металла 5 (рис. 3 а) движутся по поверхности валка. Матрица жесткости элемента K модифицируется с помощью показателя трения m. Элементы матрицы жесткости умножаются на mm _ । . При m, стремящемся к 0, элемент делается более жестким, моделируя низкое трение. При m ^ 1 моделируется “прилипание” материала к валкам. Элементы не моделируют слой смазки, но моделируют действие смазки. Каждый элемент фиктивного слоя создается на момент построения соответствующего реального элемента. Матрицы реального и фиктивного элементов могут быть сопоставлены и совместно, решены в уравнении (8). Перемещения фиктивных узлов известны, т.е они движутся как жестко связанные с валком.

Уравнения (19) для узла 5 (рис. 3 а) будут иметь следующий вид.

k 9,3 ^d 23 ⁺ k 9,4 ^d 22 ⁺ k 9,7 ^d 41 ⁺ k 9,8 ^d 42 ⁺ k 9,9 ^d 51 ⁺

⁺ k 9,10 ^d 52 ⁺ k 9,15 ^d 81 ⁺ k 9,16 ^d 82 ⁺ k 9,13 ^d 71 ⁺

⁺ k 9,14 ^d 72 ⁺ k 9,11 ^d 61 ⁺ k 9,12 ^d 62 = ^f 51 ,

k 10,3 ^d 21 ⁺ k 10,4 ^d 22 ⁺ k 10,7 ^d 41 ⁺ k 10,8 ^d 42 ⁺ k 10,9 ^d 51 ⁺

^{+ k} 10,10 ^d 52 ^{+ k} 10,15 ^d 81 ^{+ k} 10,16 ^d 82 ^{+ k} 10,13 ^d 71 ⁺

+ k 10,14d72 + k 10,11d61 + k 10,12d62 = f52 •

Так как усилие в узле 5 нормально к поверхности валка, то имеем:

fs2COSФ2 = fs 1sin Ф2 ,

Условие непроникновения поверхности валка ds 1cosф2 = ds2 sin ф2,(26)

При составлении глобальной матрицы жесткости, преобразуя уравнения (23, 24) с учетом (25,

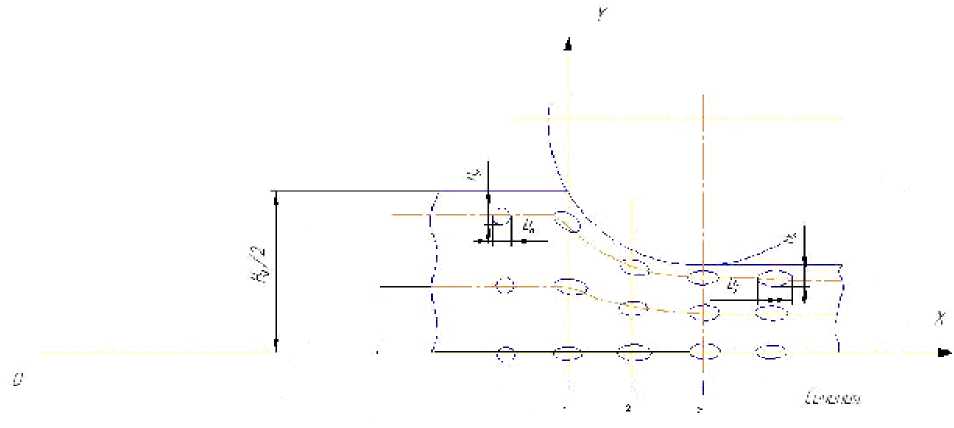
Рис. 4. Схема расположения равнопрочных вставок в очаге деформации при раскатке.

H ₀ - толщина заготовки до попадания в валки; y, x - значения координат вставки; a ₀, b ₀ и а 1 , Ь 1 - начальные и конечные размеры вставок соответственно

26), исключая f ₅₁, f ₅₂, d ₅₂ , также можно воспользоваться при решении системы (19) методом Га-уссового исключения. В ходе решения находятся значения накопленной деформации, напряжений и перемещений, т.е напряженно деформированное состояние в очаге деформации.

Проверка адекватности модели осуществляется на основе экспериментальных исследований раскатки колец, приведенных в работе [5]. В данной работе был исследован очаг деформации кольца из алюминиевого сплава АМг6, в котором по- слойно сверлились отверстия и заполнялись вставками из того же металла (рис 4). Раскатка колец с внешним диаметром 400 мм, внутренним 340 мм и толщиной 30 мм осуществлялась на кольцераскатном стане модели РМ1200 с диаметрами рабочих валков: верхнего приводного – 550 мм и нижнего неприводного – 200 мм; максимальная скорость подачи нажимного устройства составляла 16 мм/ сек.; скорость прокатки, предусмотренная конструкцией стана, соответствовала 1,5 м/сек. По результатам измерения вставок находились значения

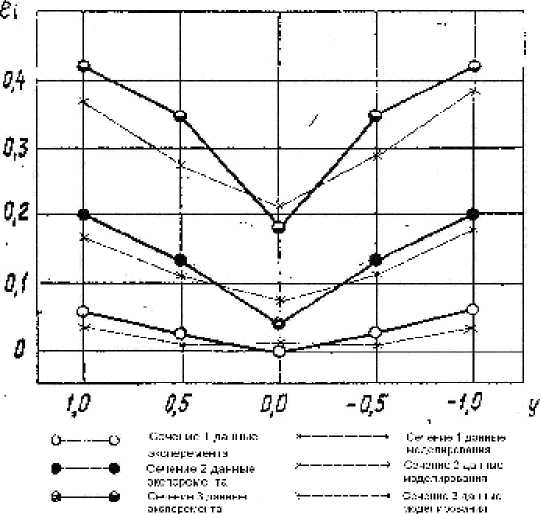
Рис. 5. Распределение интенсивности деформации по высоте очага деформации при раскатке кольцевого образца из сплава АМг6: e_i – степень накопленной деформации, y – координаты точки по оси y (причем H ₀ /2 соответствует на оси ординат 1)

деформаций и напряжений, которые представлены на рис. 5. Представленные экспериментальные данные по раскатке кольца из сплава АМг6 были введены в разработанную конечно-элементную модель. На рис. 5 сопоставлены результаты моделирования и экспериментальные данные.

Как видно из графика, результаты эксперимента и моделирования практически идентичны (сходимость около 15 %).

ВЫВОДЫ

• 1.    Для формирования в кольцевых деталях ГТД однородной макроструктуры и требуемого уровня механических свойств необходимо контролировать величину накопленной степени деформации на каждом этапе горячей раскатки заготовки.

• 2.    Разработана, конечно-элементная, модель рас-

• чета степени накопленной деформации на различных этапах деформирования кольцевых заготовок.

• 3.    Сопоставление результатов моделирования и экспериментальных зависимостей подтверждает адекватность модели.