Конечно-элементное моделирование плоской ячейки высокопористого пьезокомпозита с наклонными ребрами с учетом неоднородной поляризации
Автор: Соловьев А.Н., Германчук М.С.
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Механика
Статья в выпуске: 4 т.24, 2024 года.
Бесплатный доступ
Введение. Высокопористые композиты - металлические пены - находят широкое применение в силу своих механических свойств. В литературе представлены различные методы их математического моделирования, в том числе, на основе периодических ячеек Гибсона-Эшби. Пьезоактивные композиты обладают рядом свойств, таких как высокая чувствительность сенсоров и широкая полоса пропускания. Этим обусловлен интерес к их моделированию. Однако при построении таких моделей из пьезокерамических материалов возникает определенная трудность, связанная с выбором распределения предварительной поляризации. Следует отметить, что этот вопрос, особенно для высокопористой пьезокерамики, недостаточно изучен в литературе. Поэтому целью данной работы являлось установление влияния модели поляризации на характеристики пьезоактивного композита.Материалы и методы. Материал конструкции - пьезокерамика PZT-4, поляризация которой существенно зависит от условий ее наведения (геометрии модели, расположения электродов). Исследование разделено на два шага: в первом проводится расчет остаточной поляризации на основе теории известной в литературе, реализация которой осуществлена в пакете ACELAN; на втором решается ряд задач для ячейки композита и находится зависимость ее свойств от модели поляризации. В качестве метода решения соответствующих краевых задач электроупругости для кусочно-неоднородных тел используется метод конечных элементов, реализованный в пакете ACELAN.Результаты исследования. Решена задача определения неоднородной поляризации для двух видов конструкций плоских ячеек высокопористой пьезокерамики. Отмечены некоторые особенности полученного распределения поляризации, в частности, ее неоднородность и наличие встречной поляризации в некоторых ребрах. Решены задачи определения собственных частот и форм колебаний «внутри ячейки» и их зависимость от модели поляризации (однородной и неоднородной). Отмечается, что некоторые частоты отличаются на 10 %, а формы колебаний качественно совпадают. Проанализирована зависимость напряженно деформированного состояния и выходных характеристик от поляризации, разница некоторых значений которых достигала 15 %.Обсуждение и заключение. Процесс поляризации высокопористых пьезокерамик имеет ряд особенностей, которые необходимо учитывать для получения достоверных сведений о ее механическом и электрическом поведении. Ауксетические свойства, разница в механическом и электрическом отклике рассматриваемой ячейки напрямую связаны с этими особенностями. Таким образом модель поляризации оказывает существенное влияние на характеристики пьезоактивного композита, что определяет важность ее правильного выбора. Полученные результаты надо учитывать при моделировании представительных объемов высокопористых пьезоэлектрических композитов для определения их эффективных свойств, на основе которых строятся модели пьезоэлектрических устройств и рассчитываются их выходные характеристики.
Высокопористая пьезокерамика, неоднородная поляризация, плоская ячейка, метод конечных элементов
Короткий адрес: https://sciup.org/142243748
IDR: 142243748 | УДК: 534.1, | DOI: 10.23947/2687-1653-2024-24-4-339-346
Текст научной статьи Конечно-элементное моделирование плоской ячейки высокопористого пьезокомпозита с наклонными ребрами с учетом неоднородной поляризации
Original Theoretical Research
Finite Element Modeling of a Flat Cell of Highly Porous Piezocomposite with Inclined Edges Taking into Account Nonuniform Polarization
Arkadiy N. Soloviev 1,2 © и , Maria S. Germanchuk 2,3
-
1 Southern Federal University, Rostov-on-Don, Russian Federation
-
2 Crimean Engineering and Pedagogical University named after Fevzi Yakubov, Simferopol, Republic of Crimea
-
3 V.I. Vernadsky Crimean Federal University, Simferopol, Republic of Crimea
Introduction . Highly porous composites — metal foams — are widely used due to their mechanical properties. The literature presents various methods for their mathematical modeling, including those based on periodic Gibson-Ashby cells. Piezoactive composites have a number of properties, such as high sensor sensitivity and a large bandwidth. This is the reason for the interest in their modeling. However, when constructing such models from piezoceramic materials, a certain difficulty, associated with the selection of the distribution of preliminary polarization, arises. It should be noted that this issue, specifically for highly porous piezoceramics, has not been sufficiently studied in the literature. Therefore, the objective of this work was to establish the effect of the polarization model on the characteristics of the piezoactive composite.
Materials and Methods . The design material is PZT-4 piezoceramics, whose polarization depends significantly on the conditions of its guidance (model geometry, electrode arrangement). The study was divided into two steps: in the first, the residual polarization was calculated based on the theory known in the literature, the implementation of which was performed in the ACELAN package; in the second, a number of problems for a composite cell were solved, and the dependence of its properties on the polarization model was found. The finite element method implemented in the ACELAN package was used as a method for solving the corresponding boundary value problems of electroelasticity for piecewise inhomogeneous bodies.
Results. The problem of determining nonuniform polarization for two types of flat cell designs of highly porous piezoceramics was solved. Some features of the obtained polarization distribution were noted, in particular, its nonuniformity and the presence of counter polarization in some edges. The problems of determining natural frequencies and vibration modes “intra cell” and their dependence on the polarization model (homogeneous and nonhomogeneous) were solved. It was noted that some frequencies differed by 10%, while the vibration modes qualitatively coincided. The dependence of the stress-strain state and output characteristics on polarization, whose difference in some values reached 15%, was analyzed.
Discussion and Conclusion . The process of polarization of highly porous piezoceramics has a number of features that must be taken into account to obtain reliable information about its mechanical and electrical behavior. Auxetic properties, the difference in the mechanical and electrical response of the cell in question are directly related to these features. Thus, the polarization model has a significant impact on the characteristics of the piezoactive composite, which determines the importance of its correct selection. The results obtained should be taken into account when modeling representative volumes of highly porous piezoelectric composites to determine their effective properties, on the basis of which models of piezoelectric devices are constructed, and their output characteristics are calculated.
Acknowledgements. The authors would like to thank the Editorial board and the reviewers for their attentive attitude towards the article.
Funding Information. The research was done with the financial support from the Russian Science Foundation (no. 22–11–00302) at the Southern Federal University,
Введение . Одним из типов высокопористого композита является материал, построенный на основе ячеек Гибсона-Эшби [1] . В работе [2] проведена оценка эффективного модуля Юнга пористого титана с открытыми порами на основе трехмерного массива таких ячеек. Сравнение механического поведения моделей пен, составленных из регулярных и нерегулярных массивов открытых ячеек Гибсона–Эшби осуществляется в работе [3] . На рис. 1 а представлена открытая ячейка, на рис. 1 б и 1 в — модифицированные модели Гибсона-Эшби с наклонными ребрами для функционально-градиентных решетчатых структур [4] .

а) б) в)
Рис. 1. Схемы ячеек высокопористого композита: а — ячейка Гибсона-Эшби; б — ячейка с наклонными ребрами; в — плоская ячейка с наклонными ребрами [4]
Методы гомогенизации, которые используются при моделировании эффективных свойств композитов рассматриваются в монографиях [5, 6] . Исследования высокопористых структур, таких как, пенообразные, клеточные, ячеистые и сотовые представлены в монографиях [7, 8] , в обзорах [9 –12] и др. В работе [13] экспериментально и теоретически рассматривается поляризация пористой пьезокерамики и на основе модельного примера теоретически объясняются особенности некоторых ее эффективных свойств, о чем сказано выше. Вопрос об эффективных свойствах высокопористых пьезоэлектрических композитов в научной литературе изучен недостаточно. Это связано в первую очередь с тем, что определенную трудность составляет процесс описания поляризации таких структур. Целью данной работы явилось изучение влияния модели поляризации на напряженно-деформированное состояние ячейки и на эффективные свойства таких композитов. Рассматривается две модели: в первой предполагается однородная поляризация; во второй — распределение поляризации рассчитывается с помощью известных в литературе методов и программного обеспечения, среди разработчиков которого есть один из авторов данной работы. В работе показано, что выбор модели поляризации существенно влияет на механические свойства высокопористых пьезоэлектрических композитов.
Материалы и методы
Математическая постановка задачи . Рассматриваются плоские ячейки, которые являются элементами конструкций, представленных на рис. 1. Материал ячеек — пьезокерамика PZT-4, описываемая в рамках линейной теории электроупругости [14] , в однородном случае — поляризованная по вертикальной оси, в неоднородном случае — распределение поляризации находится по теории, предложенной в работе [15] и реализованной в конечно-элементном пакете ACELAN [16] .
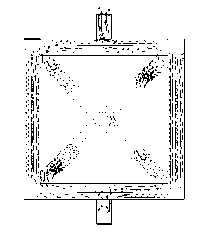
Материалы. На рис. 2 а представлена геометрия плоской ячейки, соответствующая схеме на рис. 1 а с наклонными ребрами, толщина ребер составляет 1 мм, внешний размер 10×10 мм. На рис. 2 б представлена схема неоднородной поляризации для такой конструкции, когда электроды расположены на внешних торцах верхнего и нижнего вертикальных ребер. Особенностью этой поляризации является ее неоднородность на наклонных ребрах и наличие встречных ее направлений на верхнем и нижнем горизонтальных ребрах. На рис. 2 в представлена схема поляризации для элемента композита, периодичность которого осуществляется через вертикальные и горизонтальные ребра. Особенностью поляризации этого элемента является практически неполяризованные горизонтальные ребра.
Механика

а)

в)
Рис. 2. Схемы ячеек и поляризации высокопористого композита:
а — однородная поляризация; б — неоднородная при электродах на нижнем и верхнем ребрах; в — неоднородная при электродах внизу и вверху на вертикальных ребрах
Методы. В качестве метода расчета напряженно-деформированного состояния ячеек используется метод конечных элементов (МКЭ), реализованный в пакете ACELAN [16] .
Результаты исследования . Вначале исследуются собственные частоты и формы колебаний «внутри» ячейки, представленной на рис. 1 в и 2 в . При этом ячейка закрепляется в углах по нормали на толщину горизонтальных и вертикальных ребер, что соответствует периодичности структуры композита. В таблице 1 представлены собственные резонансные частоты для однородной и неоднородной поляризации (рис. 2 в ), на рис. 3–5 — собственные формы колебаний на этих частотах.
Собственные частоты для однородной и неоднородной поляризации
Таблица 1
|
Номер частоты \ Поляризация |
Собственные частоты в Гц |
|
|
Однородная |
Неоднородная |
|
|
1 |
0,43455 × 105 |
0,41271 × 105 |
|
2 |
0,47277 × 105 |
0,47249 × 105 |
|
3 |
0,54538 × 105 |
0,49562 × 105 |
|
4 |
0,61497 × 105 |
0,58611 × 105 |
|
5 |
0,67255 × 105 |
0,67607 × 105 |
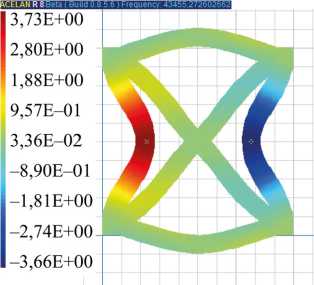
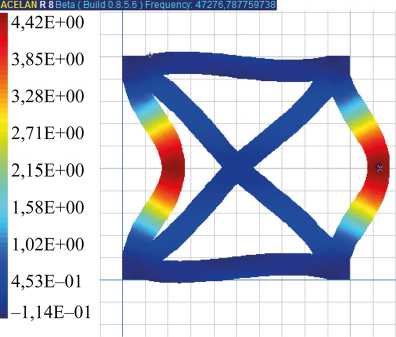
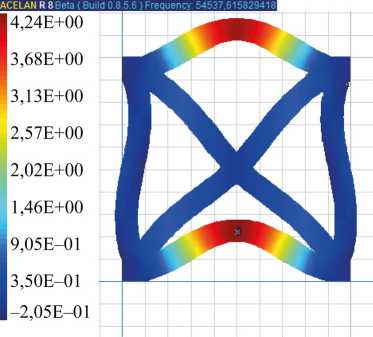
Для неоднородной поляризации 1, 3 и 4 собственные частоты ниже, чем для однородной, но формы колебаний 1–5 качественно совпадают. Поэтому на рис. 3–5 представлены собственные формы для ячейки с однородной поляризацией. На рис. 3 а, б представлено распределение горизонтальных смещений и вертикальных смещений для первой формы колебаний. На рис. 4 а, б представлены распределения для второй формы колебаний горизонтальных смещений и для третьей формы колебаний вертикальных смещений соответственно. На рис. 5 а, б представлено распределение модуля смещений на четвертой и пятой модах соответственно.
а)
Рис. 3. Первая форма колебаний однородная поляризация: а — распределение горизонтальных смещений; б — распределение вертикальных смещений
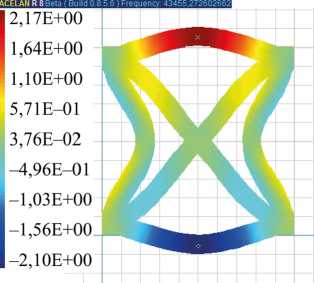
б)
а)
б)
а)
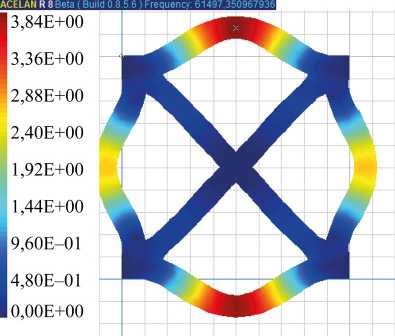
Рис. 5. Формы колебаний с распределением модуля перемещений для однородной поляризации: а — четвертая мода; б — пятая мода
Рис. 4. Формы колебаний однородная поляризация: а — вторая, распределение горизонтальных смещений; б — третья, распределение вертикальных смещений
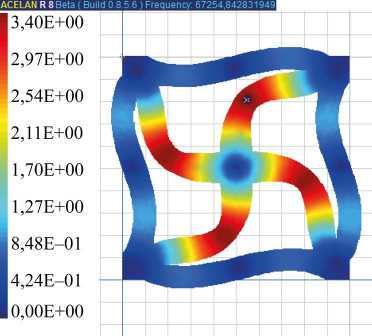
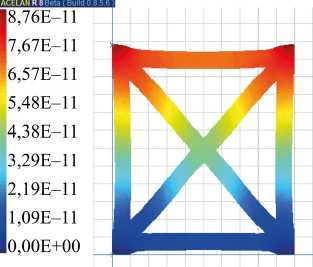
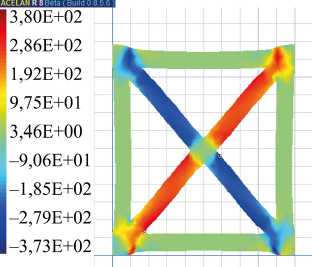
При продольном в вертикальном направлении растяжении-сжатии этой ячейки в структуре композита (моделируется свободной всей верхней поверхностью и приложением равномерного давления на верхний торец вертикальных ребер) смещение в случае однородной поляризации на 15 % больше (рис. 6 а ). Потенциал на свободных электродах на 3 % больше в случае неоднородной поляризации. Следует отметить, что касательные напряжения (рис. 6 б ) в случае неоднородной поляризации больше на 10 %. Коэффициент электромеханической связи для 7-ой моды колебаний (рис. 6 в ) на 14 % процентов больше для однородной поляризации ячейки.
а)
б)
Рис. 6. При действии вертикального давления распределение: а — вертикального смещения; б — касательных напряжений; в — распределение вертикального смещения на 7 моде колебаний
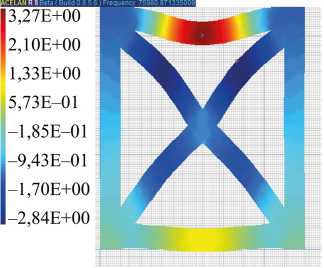
в)
Механика
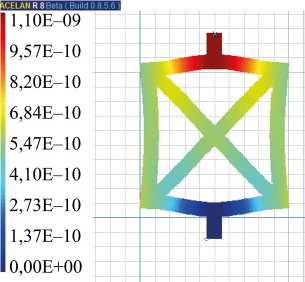
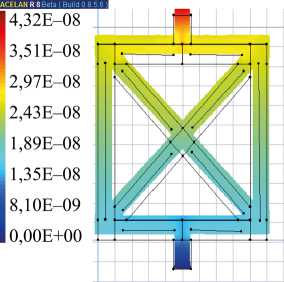
Расчеты для ячейки, представленной на рис. 2 а и 2 б, показали, что вертикальное смещение (рис. 7 а ) при действии давления на торец верхнего стержня в случае неоднородной поляризации на 11 % больше. В статике, при действии разности потенциалов на нижнем и верхнем торцах, ячейка проявляет свойства ауксетика, что связано со встречной поляризацией (рис. 2 б ) горизонтальных ребер. На рис. 7 б и 7 в приведены распределения вертикального и горизонтального смещений. Видно, что при растяжении по вертикали происходит расширение ячейки и по горизонтали.
а)
б)
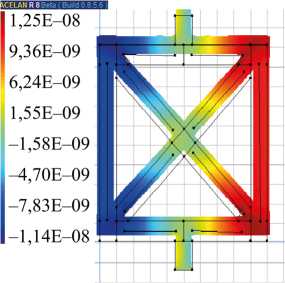
в)
Рис. 7. Распределение: а — вертикального смещения при действии вертикального давления; б — вертикального смещения при действии разности потенциалов; в — горизонтального смещения при действии разности потенциалов
Обсуждение и заключение. Таким образом, на основе этого НДС находятся эффективные свойства композитов, которые используются при моделировании пьезоэлекрических устройств, поэтому исследование влияния вида поляризации на НДС высокопористого пьезоактивного материала весьма актуально.
Расчет поля предварительной поляризации в ячейке высокопористого материала показал, что оно существенно зависит от ее геометрии и расположения электродов. К этим особенностям относится то, что некоторые ребра практически не поляризованы, другие поляризованы в одном направлении, но неоднородно и, наконец, могут появиться ребра со встречной поляризацией. Расчет механического и электрического отклика ячейки и собственных резонансных частот показал, что учет неоднородности поляризации приводит к тому, что величина расхождения этих результатов с результатами для модели с однородной поляризацией достигает 15 % и 10 % соответственно. А ячейка, с ребрами на которых есть встречная поляризация, проявляет ауксетические свойства. В работе показано, что в задачах определения эффективных свойств высокопористых пьезоэлектрических композитов на основе построения представительных объемов из его ячеек существенным является учет соответствующей их структуре неоднородной поляризации.
Практическая значимость полученных результатов связана с тем, что с помощью эффективных свойств композитов на этапе проектирования проводится моделирование, расчет и оптимизация различных пьезоэлектрических устройств (датчиков, излучателей и приемников акустических волн, пьезоэлектрических генераторов и др.).
Список литературы Конечно-элементное моделирование плоской ячейки высокопористого пьезокомпозита с наклонными ребрами с учетом неоднородной поляризации
- Gibson LJ, Ashby MF. The Mechanics of Three-Dimensional Cellular Materials. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 1982;382:43–59. https://doi.org/10.1098/rspa.1982.0088
- Никитин А.В., Михасёв Г.И. Оценка эффективного модуля Юнга пористого титана с открытыми порами на основе трехмерного массива ячеек Гибсона-Эшби. Журнал Белорусского государственного университета. Математика. Информатика. 2022;(1):75–82. https://doi.org/10.33581/2520-6508-2022-1-75-82 Nikitin AV, Mikhasev FI. Estimation of the Effective Young’s Modulus for Open Cell Porous Titanium Based on 3D Gibson-Ashby Cell Array. Journal of the Belarusian State University. Mathematics and Informatics. 2022;(1):75–82. https://doi.org/10.33581/2520-6508-2022-1-75-82
- Корниевский А.С., Наседкин А.В. Сравнение моделей пен, составленных из регулярных и нерегулярных массивов открытых ячеек Гибсона-Эшби. Вестник Пермского национального исследовательского политехнического университета. Механика. 2021;(3):70–83. https://doi.org/10.15593/perm.mech/2021.3.07 Kornievsky AS, Nasedkin AV. Comparison of Foam Models from Regular and Irregular Arrays of Gibson-Ashby Open-Cells. PNPRU Mechanics Bulletin. 2021;(3):70–83. https://doi.org/10.15593/perm.mech/2021.3.07
- Seyed Kamal Jalali, Mohammad Javad Beigrezaee, Diego Misseroni, Nicola Maria Pugno. A Modified Gibson-Ashby Model for Functionally Graded Lattice Structures. Mechanics of Materials. 2024;188:104822. https://doi.org/10.1016/j.mechmat.2023.104822
- Kachanov M, Sevostianov I. Micromechanics of Materials, with Applications. Cham: Springer; 2018. 712 p. https://doi.org/10.1007/978-3-319-76204-3
- Milton GW. The Theory of Composites. Cambridge: Cambridge University Press; 2002. 568 p. https://doi.org/10.1017/CBO9780511613357
- Scheffler M, Colombo P. (eds) Cellular Ceramics: Structure, Manufacturing, Properties and Applications. Hoboken, NJ: John Wiley & Sons; 2005. 645 p. http://doi.org/10.1002/3527606696
- Gibson LJ, Ashby MF. Cellular Solids: Structure and Properties. 2nd ed. Cambridge: Cambridge University Press; 1997. 510 p. https://doi.org/10.1017/CBO9781139878326
- Hössinger-Kalteis A, Reiter M, Jerabek M, Major Z. Overview and Comparison of Modelling Methods for Foams. Journal of Cellular Plastics. 2021;57(6):951–1001. https://doi.org/10.1177/0021955X20966329
- Chen Pan, Yafeng Han, Jiping Lu. Design and Optimization of Lattice Structures: A Review. Applied Sciences. 2020;10(18):6374. https://doi.org/10.3390/app10186374
- Srivastava V, Srivastava R. On the Polymeric Foams: Modeling and Properties. Journal of Materials Science. 2014;49:2681–2692. https://doi.org/10.1007/s10853-013-7974-5
- Firooz S, Steinmann P, Javili A. Homogenization of Composites with Extended General Interfaces: Comprehensive Review and Unified Modeling. Applied Mechanics Reviews. 2021;73(4):040802. https://doi.org/ 10.1115/1.4051481
- Вернигора Г.Д., Лупейко Т.Г., Скалиух А.С., Соловьёв А.Н. О поляризации и определении эффективных характеристик пористой пьезокерамики. Вестник Донского государственного технического университета. 2011;11(4):462–469. URL: https://www.vestnik-donstu.ru/jour/article/view/746/745 (дата обращения: 28.08.2024). Vernigora GD, Lupeiko TG, Skaliukh AS, Solovyev AN. On Polarization and Identification of Porous Piezoceramics Effective Characteristics. Vestnik of Don State Technical University. 2011;11(4):462–469. URL: https://www.vestnik-donstu.ru/jour/article/view/746/745 (accessed: 28.08.2024).
- Белоконь А.В., Еремеев В.А., Наседкин А.В., Соловьев А.Н. Блочные схемы метода конечных элементов для динамических задач акустоэлектроупругости. Прикладная математика и механика. 2000;64(3):381–393. Belokon’ AV, Eremeyev VA, Nasedkin AV, Solovyev AN. Partitioned Schemes of the Finite-Element Method for the Dynamic Problems of Acoustoelectroelasticity. Journal of Applied Mathematics and Mechanics. 2000;64(3):381–393.
- Белоконь А.В., Скалиух А.С. Математическое моделирование необратимых процессов поляризации. Москва: Физмалит; 2010. 328 с. Belokon AV, Skaliukh AS. Mathematical Modeling of Irreversible Polarization Processes. Moscow: Fizmatlit; 2010. 328 p. (In Russ.)
- Skaliukh AS, Oganesyan PA, Soloviev AN. Modeling of Piezoelectric Elements with Inhomogeneous Polarization in ACELAN. Ferroelectrics. 2015;483(1):95–101. https://doi.org/10.1080/00150193.2015.1059138


