Конечно-элементное моделирование процессов массопереноса загрязнений в производственной среде с учётом завихрений воздушных потоков

Введение. В работе [1] определение полей концентраций вредных веществ, температуры и подвижности воздуха в производственной среде исследуемых помещений осуществлялось на основе моделирования тепломассопереноса для потенциального безвихревого поля. Рассчитанные параметры производственной среды достаточно хорошо согласовывались с экспериментальными данными, полученными в помещениях с невысокой плотностью размещения стационарных источников загрязнения.

Однако у источников загрязнения, где, как правило, размещаются рабочие места операторов и местные вентиляционные отсосы, создаются условия для возникновения турбулентных га- зовоздушных потоков, которые существенно изменяют картину распределения подвижности воздуха и загрязнений в помещении, что необходимо учитывать в разрабатываемой модели. В рамках подхода, изложенного в [1], задача корректно не решается.

Таким образом, для замкнутых производственных помещений с высокой плотностью размещения источников загрязнений в условиях работы активной вентиляции возникает проблема точного определения полей подвижности воздуха с учётом вихревых движений, точность определения которых влияет на результаты расчёта полей концентраций и температур. Поэтому необходим поиск математических моделей, которые могут описывать исследуемые процессы с высокой точностью.

Обзор и анализ отечественных и зарубежных литературных источников [2, 3, 4], посвящённых процессам массопереноса веществ в замкнутых средах, показал, что реализация метода «вектор завихрённости — функция тока» имеет ряд преимуществ. Так, уравнения предлагаемого метода подобны по типу (по математическим свойствам), и их численное решение проще, чем решение уравнения Навье — Стокса.

В работе [4] рассмотрен численный анализ конвекции в прямоугольной области с источником тепла в условиях внутреннего массопереноса и внешнего вынужденного течения (1).

Постановка задачи (1), как и многих других задач вязкой несжимаемой жидкости в переменных (W,Q), обладает следующей особенностью. Граничные условия на твёрдой стенке зада- ются только для функции тока, а не для вихря, который определён лишь внутри области согласно д2Ф а2Ф    „ „                    „ уравнению —- + —- = -Q. Для преодоления этой трудности используют различные подходы, в 9X2 9Y2

частности, применяют приближённые граничные условия для вихря.

В данной работе для вихря на твёрдой стенке ставилось условие Тома, которое получалось из условия прилипания [5].

e (u ) ) a (V Q ) r₈ ²q g 2Q )

+       = u •+

5 X d Y 4d X² d Y ² J

8 2Ф  д2Ф„

—7 +--г = -Q dX2

d ( UC ) 8^/0 )    u ( 82 C 8C ) -

+      =   •     ++ dX    YY   Sc VX2 dY2J

U = д Ф/ 8X

-C = дФ/ YY, гдеX,Y — координаты Декартовой системы координат; U,V — составляющие скорости в проекции на оси X,Y соответственно; Ψ — функция тока; Ω — завихрённость скорости; С — концентрация примеси в области решения; Q — источник загрязнения.

Система (1) не может быть решена в общем виде аналитически, для нахождения решения необходимо использовать численные методы, реализация которых возможна в программной среде FlexPDE -6.20.

Постановка задачи. Объект исследования (рис. 1) представляет собой воздушную камеру с входными и выходными воротами и расположенным по центру источником выброса оксида углерода. Скорость газа поступающего в камеру является постоянной в течение всего процесса.

Рис. 1. Воздушная камера с источником загрязнения

Вихревая модель массопереноса вредных веществ. Для универсальности система уравнений (1) была приведена к безразмерному виду, а безразмерные переменные величины приняли следующий вид:

X = XL , Y = Y/L x , C = CC s /, U = UJU n , C = C)U „ ,

W = ф/( U n • L x ) , 5^ = Q • L x U n , Q ) = Q • L x I C S_S • U n ) , где X. ,Y — безразмерные координаты, соответствующие координатам X,Y; L x — длина области решения по оси; U,С — безразмерные скорости, соответствующие скоростям U,C ; U n — скорость потока на входе в воздушную камеру; Ф — безразмерный аналог функции тока; Q — безразмерный аналог вектора вихря; C — безразмерная концентрация примеси; C_S — концентрация источника; Q — безразмерный аналог источника.

Для повышения сходимости решаемых уравнений в среде FlexPDE-6.20 в модель был введён поправочный коэффициент ( Re ), который привёл исследуемые величины к одному порядку. Система уравнений (1) приобрела вид:

⁸( U й ) г р й )     1       _:, д 2 й х

8 Х 8 Y   Re (д X ² 8 Y ² J

82ф 82ф

+  —

8 Х ²   8 Y Y

= -V Re ■ й

8 ( UC ) 8 ( VC )

— +     _

8 Х      8 Y

Sc ■

Re

( д^гс д^гс ) (д Х ²   8 Y ² J

+ _xRe ■ Q

U = 8 Ф / 8 Х

-     ~

-V = 8Ф / 8Y, где U = U ■ 'jRe, V = V ■ ^Re, Ф = Ф ■ VRe — скорости и функция тока системы уравнений с по- правочным коэффициентом (2).

Граничные условия на входе в воздушную камеру:

Ф = Y ■ 4ёё,  й = 0, с = 0 .

Граничные условия на выходе:

8 Х = 0, й = 0, 8 C/ 8 Х = Y 1 / Y 2 ■ C ■ Sc ■ Re .

Граничные условия на стенках воздушной камеры [4, 5]:

нижняя: Ф = 0,

й =

2 - ( Ф е - Ф 1 ) V Re ■ th '

правая: Ф = Y 1 ■ ^Re

й =

2 ■ ( Ф е - Ф 1 )

V Re ■ th '

верхняя: Ф = Y 1 ■ ^Re

й =

2 ■ ( Ф 0 - Ф 1 )

V Re ■ th '

левая: Ф = Y 1 ■ ^Re

й =

2 ^ ( Ф 0 - Ф 1 )

V Re ■ th '

8 C/8 Х = 0;

8 C/8 Х = 0;

8 C/8 Х = 0 ;

8 C/8 Х = 0 ,

где Ω — значение вектора завихрённости на границе; h — безразмерная длина отрезка от граничной точки «0» до ближайшей к границе точки «1» (безразмерная величина приграничного слоя); Ψ0 и Ψ1 — значения функции тока на граничной точке «0» и приграничной точке «1» соответственно.

Численные решения на основе метода конечных элементов. В рассматриваемой модели присутствует параметр, связанный с формулировкой граничных условий ( h ). Были произведены расчёты определения диапазона изменения безразмерной величины приграничного слоя ( h = h / L x ), влияющего на сходимость решения.

На рис. 2 показаны результаты расчётов исследуемых параметров (функция тока, вектор завихрённости, скорости и концентрация) при значении приграничного слоя h = 0,01 ■ L , где

L = 1 — безразмерная длина камеры.

а)

в)

Рис. 2. Результаты расчётов функции тока (а), вектора завихрённости (б), скорости (в) и концентрации (г) при значении

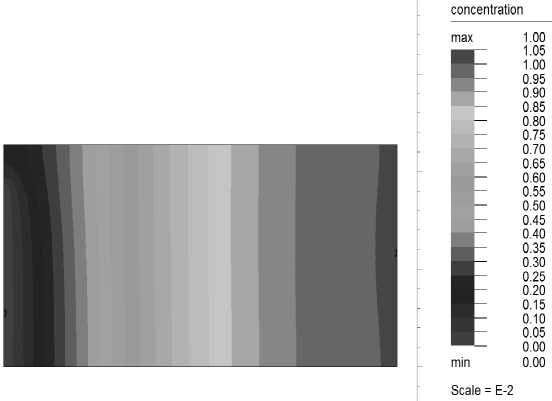
г)

приграничного слоя h = 0,01 ■ L , где L = 1 — безразмерная длина камеры

На рис. 3 показаны результаты расчётов исследуемых параметров при значении пограничного слоя h = 0,001 ■ L .

Таким образом, определена величина h , при которой система устойчива (рис. 2), и, как видно из рис. 3, а, уменьшение величины h приводит к невозможности получить сходимость решения.

В математической модели также менялась величина входной скорости. Диапазон значений скорости U_in (от 0,1 м/с до 0,6 м/с) был принят в соответствии с санитарно-гигиеническими нормативами. Однако сходимость решения при данных параметрах скорости не наблюдалась.

Сходимость наблюдалась в диапазоне скоростей (рис. 4), значительно ниже реальных величин ( U n = 10 4 м/с и менее).

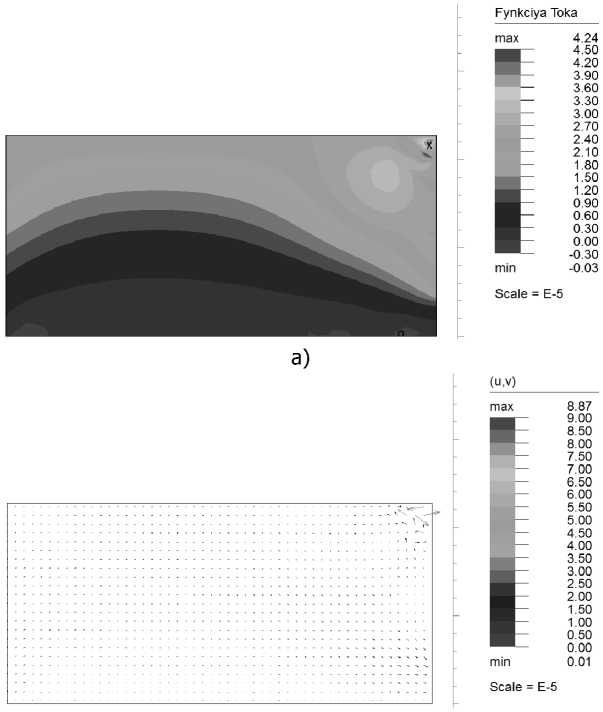
в)

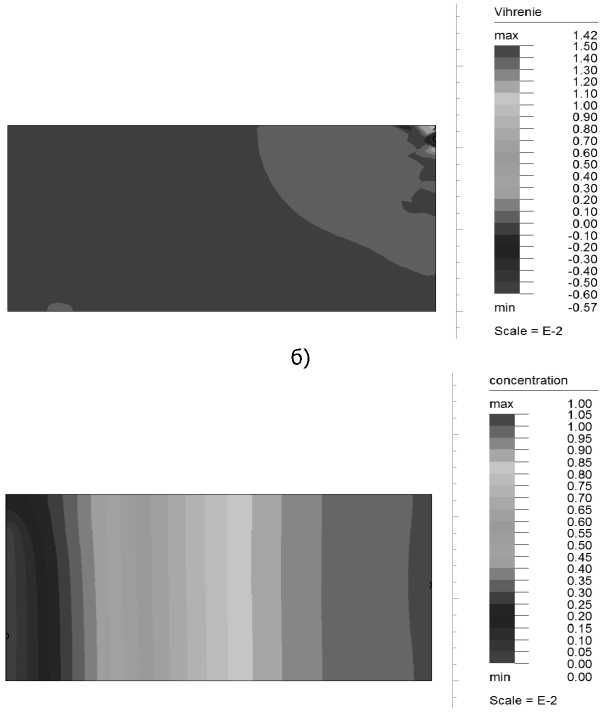
г)

Рис. 3. Результаты расчётов во FlexPDE функции тока (а), вектора завихрённости (б), скорости (в) и концентрации (г) при значении пограничного слоя h = 0,001 • L

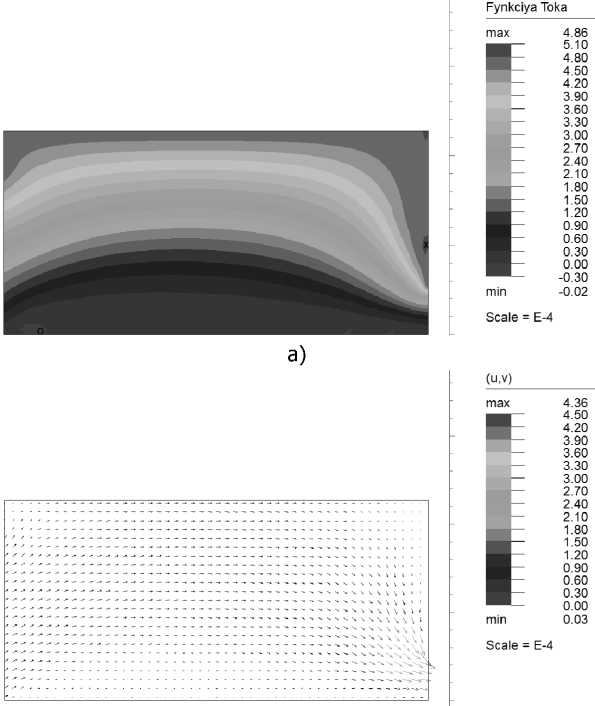
в)

г)

Рис. 4. Результаты расчётов во FlexPDE функции тока (а), вектора завихрённости (б), скорости (в) и концентрации (г) при

U n = 10 4 м/с

Заключение.

• 1.    Проведённые численные эксперименты доказали, что решение исследуемых уравнений в диапазоне нормированных скоростей неустойчиво.

• 2.    Необходим переход к более производительной программной среде, например ANSYS или Solid works.