Конечно-элементное моделирование совместной работы оползня скольжения и защитного сооружения

УДК 539.42                                               

Введение. Проектирование противооползневых инженерных сооружений является одним из важнейших направлений в области строительной науки. Вместе с тем, численное моделирование устойчивости склонов естественного залегания связано с факторами неопределенности такими, как нестабильность физикомеханических характеристик материала и вариативность траекторий разрушения.

В настоящее время для оценки устойчивости откосов используют различные варианты метода предельного равновесия и метод снижения сдвиговой прочности материала в сочетании с методом конечных элементов [1– 3]. Результатом расчета по методу предельного равновесия является геометрия «классической» круглоцилиндрической линии скольжения. Метод снижения прочности позволяет получить более полную информацию о поверхности скольжения для рассматриваемого оползневого участка.

Отдельно можно выделить направление исследования склоновых процессов, базирующееся на модели движения центров масс частиц, упруго взаимодействующих между собой и наклонной поверхностью [4]. Еще одним подходом, базирующимся на блочной кинематике, является так называемый метод разрывного анализа деформаций (в оригинале discontinuous deformation analysis DDA) [5]. Метод DDA имеет ограничения, касающиеся взаимодействия между смежными блоками. Суть этих ограничений состоит в невозможности взаимного проникновения блоков и отсутствии растягивающих напряжений между блоками. На рис. 1 (взят из [5]) приведена схема связи блоков, используемая в методе DDA для моделирования обвалов горных пород. На этом рисунке k _x , k _y и c _x , c _y — параметры жесткости и вязкости соответственно в направлении осей X и Y .

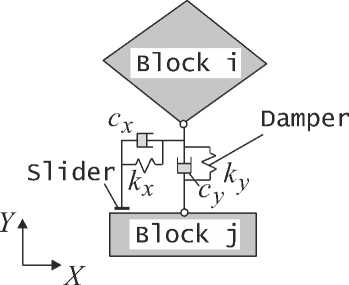
Рис. 1. Схема связи блоков для моделирования обвалов горных пород

Недостаток метода DDA состоит в отсутствии возможности введения в расчетную схему инженерных сооружений, препятствующих прогрессирующему разрушению горного массива.

Если после оценки устойчивости склона естественного залегания принимается решение о целесообразности возведения противооползневых сооружений, то в качестве исходной информации для проектирования используют данные инженерно-геологических изысканий, а также различные сценарии внешних силовых воздействий на участках оползневого склона. Численное моделирование напряженно-деформированного состояния укрепленного оползневого склона выполняют, как правило, в двумерной постановке в рамках нелинейной теории упругости с помощью метода конечных элементов. Давление грунта полагается линейно-распределенным по глубине. Для инженерных геотехнических расчетов используют специализированные конечно-элементные программные комплексы: Plaxis, MIDAS GTS, GEO5, включающие наиболее распространенные модели грунта. Моделирование сложных геотехнических систем осуществляют на базе «тяжелого» программного комплекса ANSYS Mechanical [6].

Отметим, что в работах, посвященных анализу напряженно-деформированного состояния противооползневых сооружений отсутствуют сведения о применении моделей, учитывающих непосредственное скольжение (сползание) оползневого слоя. Обычно используются расчетные схемы, в которых обеспечивается совместное (безотрывное) деформирование всего грунтового массива, вплоть до потери несущей способности грунта. Это не позволяет в полной мере оценить силовое воздействие оползневого слоя на элементы конструкции.

Материалы и методы. Расчетная схема оползневого склона показана на рис. 2 (размеры указаны в метрах). Считаем, что склон состоит из двух слоев: S1 — основание склона (плотная глина); S2 — оползневой слой (переувлажненный суглинок). Полагаем, что положение линии скольжения известно. Внешнее воздействие представлено собственным весом оползневого слоя S 2 и равномерно распределенным давлением q .

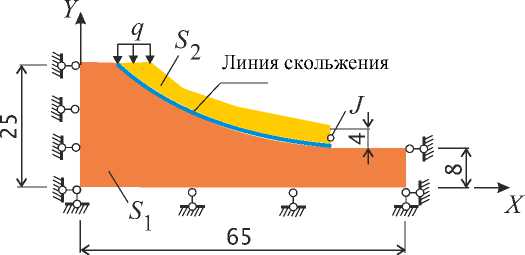
Рис. 2. Расчетная схема оползневого склона (размеры указаны в метрах)

Механические характеристики материалов слоев приведены в таблице 1.

Механические характеристики слоев склона

Таблица 1

Материал	Модуль деформации E , МПа	Коэффициент Пуассона V	Угол внутреннего трения ф , град	Сцепление с , кПа	Плотность р , кг/м 3
слой S 1	21	0,30	15	45	1702
слой S 2	12	0,35	22	22	1800

Численное моделирование выполняем с помощью программного комплекса ANSYS Mechanical. Конечно-элементная модель склона показана на рис. 3. Для моделирования грунта использованы двумерные 4-х узловые конечные элементы PLANE42. Причем сетки слоев S ₁ и S ₂ топологически не связаны, т. е. вдоль линии скольжения каждый узел имеет двойную нумерацию. Это необходимо для моделирования возможного смещения слоя S ₂ относительно слоя S ₁ .

Для описания поведения слоев склона используем модель идеально упругопластического материала Друкера-Прагера [7], которая включена в комплекс ANSYS Mechanical. Уравнение поверхности текучести для данной модели имеет вид

F = ^Т i + 3 РСТ m -СТ _у = 0, где т i — интенсивность касательных напряжений;

ст m — среднее напряжение;

Механика

в , ст y — параметры модели, связанные с константами материала C и ф соотношениями:

2sin ф             6 C cos ф в = I      —; ст = ,      ==.

^3 ( 3 - sin ф )      ⁷    V 3(3 - sin ф )

Физическая зависимость, устанавливающая связь между напряжениями и деформациями, для идеально упругопластического материала описывается выражением [8]

_T = _GY__ ■                                      ,

1 + y. GI т i          пр где Yi — интенсивность деформаций сдвига; G — модуль сдвига; касательное напряжение, соответствующее пределу прочности материала (рис. 4)

^т пр = C ■ ^ -.Ш ^ф-

Y

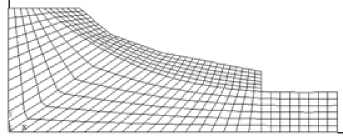
Рис. 3. Конечно-элементная модель склона

^т .

т

Y ,

X

Рис. 4. График т. ~ у .

Эффект возможного скольжения слоя S 2 относительно слоя S 1 моделируем с помощью комбинированных элементов пружинного типа COMBIN14 (рис. 5)-

Уравнение равновесия для пружинного КЭ имеет вид

[h]{и} ={Р}, где [ h ] — матрица жесткости; {и}, {p} — векторы столбцы узловых перемещений и сил. В зависимости от ориентации пружинного элемента имеем:

— локальная ось	КЭ ^ совпадает с осью x
	" 1  0   - 10 "
	0 0 0 0	{ и } = { и., 0 и „ 0} T ;
[ h ] = k x	- 10 10	;
	_ 0   0   0   0 _	{ p } = { p .x 0 p„ 0} T
— локальная ось КЭ ^ совпадает с осью у
	" 0   0   0   0 "
	0 10 - 1	{ и } = {0 U y 0 и, у } T ;
[ h ] = к.		;
y	0 0 0 0
	_ 0 - 10  1 _	{ p } = {0 p .y 0 p ,y } T

Здесь k_y , k x — коэффициенты жесткости, соответствующие ориентациям пружины вдоль осей x и у ; T — символ операции транспонирования.

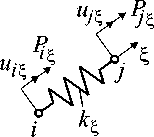
0          x

Рис. 5. Комбинированный конечный элемент COMBIN14

Принимаем следующие значения коэффициентов упругости:

к = 21 Н/м, к = 100 Н/м. y                    , x

Параметры вязкости: c_x = c y = 0,5 Н^с/м.

При назначении коэффициентов к_у и к_х преследовалась цель приблизить модель рассматриваемого склона к реальности. В частности, вдоль линии скольжения учесть сопротивление деформации сдвига и упругий отпор слоя S ₂. Аналогичный подход к моделированию эффекта «проскальзывания» использован в [9]. Отметим, что в принятой дискретизации слоев узлы . и j , принадлежащие пружинным элементам, совпадают.

Расчетная нагрузка включает собственный вес слоя S ₂ и равномерно распределенное усилие q , прикладываемое к верхнему торцу слоя S ₂ (рис. 2).

Для организации вычислительного процесса используем нелинейный «решатель» комплекса ANSYS Mechanical, в котором реализован метод Ньютона-Рафсона.

Для верификации конечно-элементной модели выполним оценку устойчивости рассматриваемого склона, исключив из расчетной схемы элементы COMBIN14 и получив, таким образом, неослабленную модель. Расчетным путем установлено, что для неослабленного склона предельное значение давления q , при заданных механических характеристиках слоев S ₁ и S ₂ , составляет 400 кПа. Процесс работы нелинейного решателя отражен в виде графика на рис. 6. Здесь вдоль оси абсцисс откладывается общее число итераций на каждом шаге «Time» нагружения, по оси ординат соответствующие нормы невязки усилий «F» и перемещений «U». Параметр «Time» изменяется в диапазоне от 0 до 1. Итерационный процесс продолжается до тех пор, пока значения «F»–«L2» меньше величин «F»–«CRIT». Пересечение пика пилообразной линии «F»–«L2» и кривой «F»–«CRIT» свидетельствует о том, что в данном примере итерационный процесс «сошелся» с заданной точностью.

На рис. 7 приведена картина распределения горизонтальных перемещений u _x в теле неослабленного склона при q =400 кПа. Как следует из рисунка, потеря устойчивости склона носит локальный характер. При этом отчетливо прослеживается круглоцилиндрический вид линии скольжения. Соответствующее распределения поля интенсивности пластических деформаций сдвига γ _i показано на рис. 8.

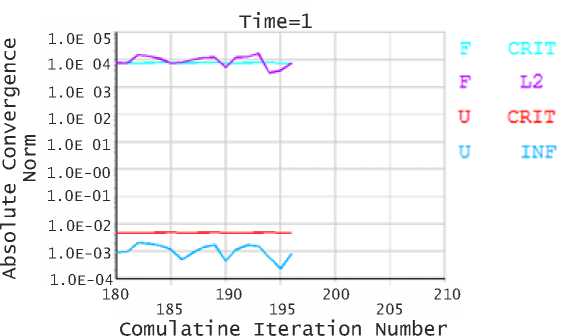
Рис. 8. График сходимости процедуры Ньютона-Рафсона

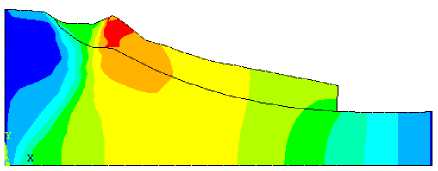
u_x , м -.015463 .00129 .018043 .034796

--- .051549 .0 68302

РР .085055 рр .101808 □ .118561 □ .135314

Рис. 7. Визуализация перемещений u _x при q =400 кПа

Механика

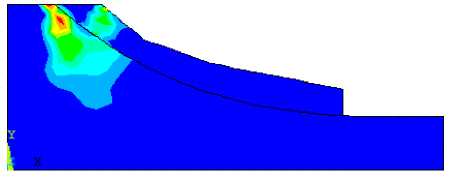
Рис. 8. Визуализация распределения γ _i при q =400 кПа

γ _i

-.032265 -.014542 .00318 .020902 .038624 .056347 .074069 .091791 .109513 .127236

Результаты исследования. С целью моделирования эффекта кинематической неустойчивости оползневого слоя S ₂ выполним анализ напряженно-деформированного состояния склона с учетом ослабления при различных значениях давления q . Подчеркнем, что в этом случае элементы COMBIN14 включены. На рис. 9 представлен график u_x ~ q , где u _x — горизонтальное перемещение точки J «языка» оползневого слоя

S ₂ (рис. 2).

Сопоставляя результаты расчетов для ослабленного и неослабленного склонов, приходим к выводу, что включение в расчетную модель слоя скольжения существенно (более, чем на один порядок) снижает предельное значение q .

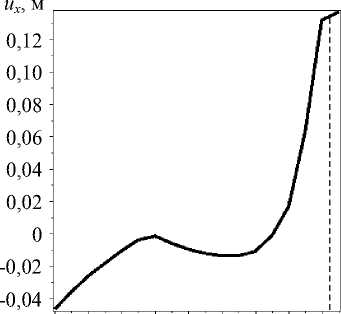
0 2  4 6   8 10 12 14 16 q , кПа

Рис. 9. График зависимости горизонтального перемещения точки J «языка» оползневого слоя S ₂ от значения давления q

Из графика u_x ~ q видно, что для рассматриваемой модели склона оползневой процесс имеет явно выраженный нелинейный характер. Причем в диапазоне давлений от 6 кПа до 11 кПа наблюдается смещение «языка» слоя S ₂ в направлении, обратном ожидаемому оползневому процессу. На рис. 10 показана контрастная картина распределения поля перемещений в направлении оси x , соответствующая нагружению слоя S ₂ давлением q =16,5 кПа.

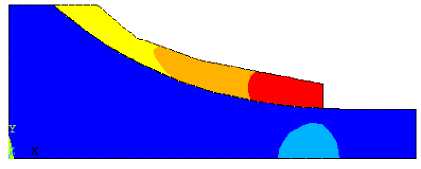
Рис. 10. Визуализация перемещений u _x при q =16,5 кПа

u_x , м

Фрагмент конечно-элементной модели «языка» оползня в деформированном состоянии при q =16,5 кПа представлен на рис. 11.

Рис. 11. Визуализация конечно-элементной модели фрагмента склона в деформированном состоянии при q =16,5 кПа

Как видно из рис. 11, предлагаемая методика позволяет моделировать эффект скольжения слоя S ₂ относительно слоя S ₁ . Данный эффект проявляется в относительном смещении узлов сетки (показано стрелкой). Величина максимального относительного смещения u _{x max} достигает 18,2 см, что с физической точки зрения вполне соответствует началу оползневого процесса.

На рис. 12 представлены рассматриваемые варианты схем противооползневых сооружений, выполненных из бетона. Приняты механические константы для бетона E = 3∙10 4 МПа; ν = 0,2; ρ = 2446 кг∕м 3 . Расчетное значение высоты защитных сооружений h =2,6 м. Заглубление свайного основания 8 м (схемы б и в ). Значение давления q = 16,5 кПа.

Свайное основание (схема б ) и шпунтовое ограждение (схема в ) представлены 2-х узловыми балочными элементами BEAM3. Диаметр свай принят равным 0,35 м.

Визуализация рассматриваемых схем противооползневых сооружений в деформированном состоянии показана на рис. 13. Из приведенных данных следует, что при моделировании оползневого процесса происходит вдавливание «языка» слоя S ₂ в основание S ₁ . Этим объясняется «заваливание» противооползневых сооружений навстречу движению слоя S ₂ .

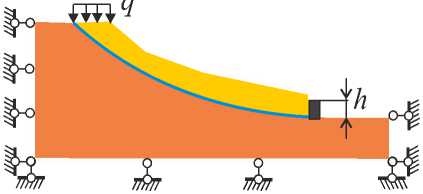
a)

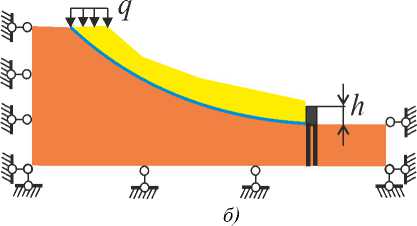
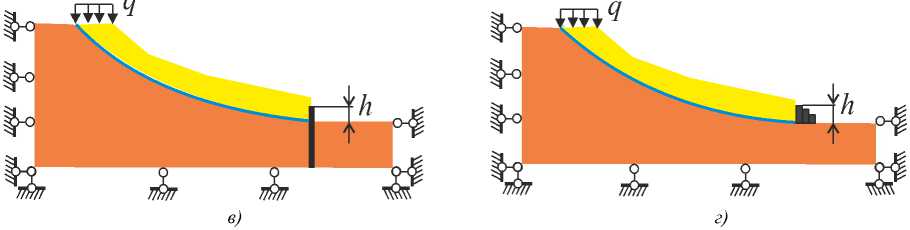
Рис. 12. Схемы противооползневых сооружений:

а — подпорная стенка, б — подпорная стенка на свайном основании, в — шпунтовое ограждение, г — габион

Графики изменения горизонтальных перемещений u_x и напряжений σ _x по высоте h рассматриваемых защитных сооружений приведены на рис. 14.

Механика

Анализируя представленные результаты, приходим к выводу, что наиболее выраженным с инженерной точки зрения противооползневым эффектом обладает схема б, обеспечивающая относительно однородное горизонтальное смещение подпорной стенки без «заваливания». При этом максимальное горизонтальное смещение стенки составляет 16 мм. Для усиления надежности данной конструкции можно применить анкерные связи [10].

Определенный практический интерес при проектировании противооползневых сооружений представляет характер распределения внутренних усилий в свайном основании. Для схемы б эпюры изгибающих моментов M , возникающих в левой и правой сваях, представлены на рис. 15. Значение максимального нормального напряжения сжатия при изгибе для схемы б составило σ max = 337кН/м 2, что значительно меньше предела прочности бетона при сжатии (25,5 МПа).

а)

б )

в )

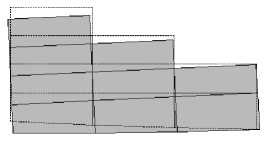
г )

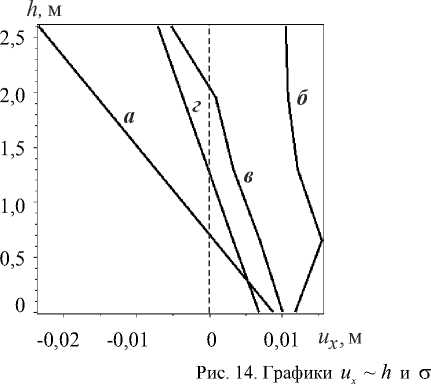
Рис. 13. Визуализация защитных сооружений в деформированном состоянии: а — подпорная стенка, б — подпорная стенка на свайном основании, в — шпунтовое ограждение, г — габион

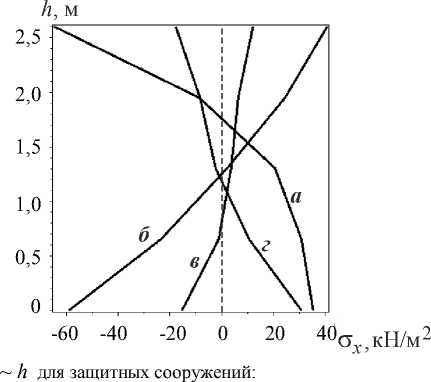
а — подпорная стенка; б — подпорная стенка на свайном основании; в — шпунтовое ограждение; г — габион

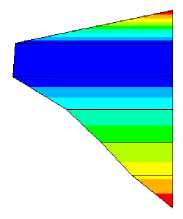
М , Н∙м

-7915.24

-7035.77

РР -6156.3

РР -5276.83

--- -4397.36

РР -3517.83

РР -2638.41

РР -1758.94

-879.472

.367Е-03

а)

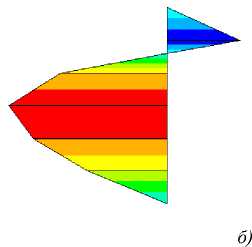
М , Н∙м

-1951.45 ■ -1263.85 РР -576.257 РР 111.338 --- 798.932 РР 1486.53 РР 2174.12 РР 2861.72 = 3549.31 ■ 4236.91

Рис. 15. Эпюры изгибающих моментов в сваях схемы б на рис. 12: а — левая свая; б — правая свая

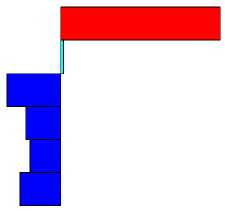
Эпюры поперечных сил Q в сваях приведены на рис. 16.

а)

Q , Н

-1956.41 ■ -1096.54 РР -236.674 РР 623.194 РР 1483.06 РР 2342.93 РР 3202.8 РР 4062.67

4922.54

5782.41

б)

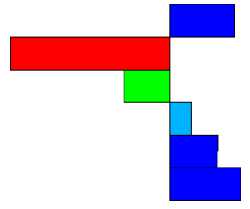
Q , Н -1608.21 -1028.98

РР -449.75

РР 129.477

--- 708.705

РР 1287.93

РР 1867.16

РР 2446.39

3025.62

3604.84

Рис. 16. Эпюры поперечных сил в сваях схемы б на рис. 12: а — левая свая; б — правая свая

Из рис. 16 видно, что сечение возможного среза свай располагается ниже нулевой отметки сооружения.

Обсуждение и заключения. В рамках задачи о плоской деформации построена конечно-элементная модель, имитирующая оползневой процесс склона естественного залегания. В отличие от существующих методик расчета противооползневых сооружений, в данном подходе реализована концепция кинематической неустойчивости оползневого слоя, суть которой состоит в применении вдоль предполагаемой линии скольжения комбинированных конечных элементов. На серии численных экспериментов выполнена апробация предлагаемой методики исследования взаимодействия оползня скольжения с различными вариантами защитных сооружений. Установлено, что наиболее эффективную противооползневую защиту при заданных геометрических и физических параметрах обеспечивает комбинированное сооружение, состоящее из подпорной стенки и свайного основания.