Конечно-элементный расчет цилиндрической оболочки, податливой при трансверсальном сдвиге

Автор: Нестеров В.А.

Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau

Рубрика: Математика, механика, информатика

Статья в выпуске: 2 (48), 2013 года.

Бесплатный доступ

Рассматривается новый конечный элемент оболочки, в расчетах которой учитывается трансверсальный сдвиг. При этом в каждом из узлов конечного элемента в качестве основных кинематических параметров присутствуют осредненные по толщине углы трансверсального сдвига. Представлены результаты численного исследования, демонстрирующие отсутствие эффекта сдвигового запирания в новой оболочечной конечноэлементной модели.

Балка, трансверсальный сдвиг, метод конечных элементов, эффект сдвигового запирания

Короткий адрес: https://sciup.org/148177081

IDR: 148177081

Текст научной статьи Конечно-элементный расчет цилиндрической оболочки, податливой при трансверсальном сдвиге

Композитные конструкции, обладающие высокими удельными механическими характеристиками, находят широкое применение в производстве авиационной и ракетно-космической техники. Ряд особенностей композитных материалов резко выделяет их из ряда традиционных конструкционных материалов, что вынуждает разрабатывать новые расчетные модели, в которых адекватным образом учитываются эти особенности. Главная среди них – низкая сдвиговая жесткость по отношению к трансверсальным напряжениям. Учет данного обстоятельства приводит к повышению порядка разрешающих уравнений за счет введения в рассмотрение углов трансверсального сдвига.

В настоящей работе рассматривается новый четырехугольный конечный элемент оболочки, среди основных узловых переменных которого присутствуют углы трансверсального сдвига. Разработанная модель основывается на математической теории пластин Рейсснера– Мидлина. Вывод основополагающих уравнений и матриц теории метода конечных элементов выполняется вариационным методом, который предполагает использование в качестве исходного выражения полной потенциальной энергии для элемента оболочки. Основные преобразования при этом касаются выражения потенциальной энергии деформации, которое в геометрически нелинейной постановке для сдвиговой модели имеет вид

_ 1г 1 2 1 1 2 1

U = 2 Щ N “ l ^S “ ⁺ 2 ^Ю “ 1 ⁺ N ₽ l ^s ₽ ⁺ 2 ® ₽ 1 ⁺

⁺ N ар ( ⁸ ар ^+е ра + ® а ® р ) ⁺ M а ^Х а ⁺ M р / р ^{+ (1)}

+ Mар (Хар + Хра ) + Qa Va + Q Vp } dа dР , где N, Q, M – внутренние погонные усилия; ε, χ – обобщенные деформации начальной поверхности, ω – углы поворота бесконечно малого элемента оболочки.

Рассмотрим цилиндрическую оболочку радиусом R , нагруженную давлением p . Криволинейную систему координат свяжем с начальной поверхностью, где ось x направлена вдоль образующей цилиндра, ось y – по окружности начальной поверхности, ось z – по нормали к ней. Запишем функционал Лагранжа для задачи статического расчета в геометрически линейной постановке. Выражение потенциальной энергии деформации (1) в данном случае примет следующий вид:

U = 2 Л (Nx S x + Ny S У + NxyS xy + Mx Х x + + My Х y + Mxy Х xy + Qx V x + Qy V y ) dxdy, где внутренние погонные усилия связаны с обобщенными деформациями начальной поверхности с помощью следующих физических соотношений:

N x = B 11 ^S x ⁺ B 12 ^S y ⁺ ^С11 ^Х x ⁺ ^С 12 ^Х y ,

N y = B 21 ⁸ x ⁺ B 22 ⁸ y ⁺ C 21 ^х x ⁺ C 22 ^х y ,

N xy = B 33 ⁸ xy ⁺ C 33 ^Х xy , ⁽³⁾

M x = C 11 ^S x ⁺ C 12 ^S y ⁺ D 11 ^X x ⁺ D 12 ^X y

M y = C 21 ⁸ x ⁺ C 22 ⁸ y ⁺ D 21 ^Х x ⁺ D 22 ^Х y ,

Mxy = C33еxy + D33Хxy , Qx = Kx Vx , Qy = Ky Vy , где B, C, D и K – жесткостные параметры: В определяют мембранную жесткость оболочки, С – так называемая смешанная жесткость, D – изгибная жесткость, К – жесткость оболочки при трансверсальном сдвиге.

Обобщенные деформации определяются следующими геометрическими соотношениями:

( 8vy 1 8v 82 w I ( \ 5и

+ D 22-- +----- T + B 33 I+I

| 8y R 8y 8y2 J 18y8

( 8 и 8 v V8V, ^8v y 1 8 v , 8 ² w

+ 2C331 + I ++

18y 8xJI 8y 8x R 8x8

I +

X x

8 и 8 v w 8 и 8 v

, ^ y =+ , ^ xy =+

8 x ^y 8y R ^y 8 y 8 x

I 8V, ^8v y 1 8 v , 8 ² w | + D ₃₃ —— + — y +---2--- +

I 8 y 8 x R 8 x 8 x 8 y J

8x ’

86 y

X y ₂

8 y

86 86y x„. = —- +—y y 8y 8x

⁺ K x V 2 ⁺ K y V 2 } ^d xdy .

6 x = V x

8 w

8 x

⁶ y = ^V y ⁺ ~d^-

8 w

8 y

В выражении (4) фигурируют следующие кинематические параметры: θ x и θ y – углы наклона сечений, измеряемые в плоскостях xz и yz соответственно, u и v – перемещения точек начальной поверхности вдоль осей x и y соответственно, w – прогибы точек начальной поверхности, ψ _x и ψ _y – углы сдвига или осреднен-ные по высоте сечения деформации трансверсального сдвига, вычисляемые по следующим формулам [1]:

1 h - 5 i h - 5

V x =- e ed_zdz , V y =7 J e yz^dz , (5)

где h – толщина оболочки, ( h – s ) и (– s ) – координаты по высоте верхней и нижней поверхности оболочки соответственно.

С учетом соотношений (4) для углов наклона сечений (θ x и θ y ) представим выражения для кривизн в виде

8v, 8 ² w ^8vy 1 8 v 8 ² w

X,. = , x.. = —- + ,

8 x 8 x ² y 8 y R 8 y 8 y ²

8v, 8V 1 8 v8

X xy = —— + —- +---2---.(6)

y 8y 8x R 8x8

Подставим физические (3) и геометрические (4), (6) соотношения в подынтегральное выражение (2). В ре-

зультате получим

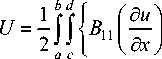
8 и ( 8v x 8 ² w

8 x I 8 x 8 x ²

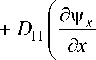
8 w I „ 8 и (8 v w I —— + 2 B ₁₂— I —+ — 1 +

8 x ² ^J 8 x 18 y R J

„ (8 v w I

+ Bn ~ ।—

²² (8 y R J

8 и ( ^8v y 1 8 v 8 ² w I

+ 2 C ₁₂— —^y- +----- +

8 x (8 y R 8 y 8 y ² J

+ 2 C 12

(8 v w I( 8v x 8 ² w I

—+— I T + (8 y R J( 8 x 8 x ² J

+ 2 D„ ' ^V ¹² ( 8 x

8 ² w V^8v y 1 8 v 8 ² w I

-т^ ^{+ +}

8 x ² J ( 8 y R 8 y 8 y ² J

( 8 v w V ^8v y 1 8 v 8 ² w I

+ 2 C ₂₂I— + — I —- +----- +

18 y R J | 8 y R 8 y 8 y ² J

Здесь a и b определяют границы элемента оболочки вдоль оси x , а c и d – вдоль оси y .

Потенциал внешних сил для цилиндрической оболочки, нагруженной давлением p , определяется следующим интегралом:

П = JJ pwdxdy . ⁽⁸⁾

Выражение полной потенциальной энергии цилиндрической оболочки имеет вид

E = U + П . (9)

Здесь потенциальная энергия деформации задается интегралом (7), а потенциал внешних сил – интегралом (8).

Функционал (9) позволяет получить разрешающие уравнения теории МКЭ. Будем рассматривать модель с сеткой прямоугольных конечных элементов с внутренней нумерацией узлов, осуществляемой при обходе контура против часовой стрелки.

Вектор узловых кинематических параметров δ е имеет следующий вид:

δе = {δ1 δ2 δ3 δ4}Т,(10)

где δ i ( i = 1, 2, 3, 4) – вектор кинематических параметров i -го узла:

I (8 w I I 8 w iI

8, = < w_z — — V,/ Vw и, v r . (11)

ixiyiii

I 18x j i 18y J iI

Кинематические параметры можно выразить через их узловые значения следующим образом:

( 8 w I \ 8 w )

w = P 11 ^w 1 ⁺ P 12\ — I ⁺ Р 1з |^1 ⁺ P 18 ^w 2 ⁺

1 8 x J 1 1 8 y J 1

( 8 w I | 8 w | ( 8 w I

⁺ P 19 I I ⁺ P 1,1o I ^I ⁺ P 1,15 ^w 3 ⁺ P 1,16 I ^I ⁺

1 8 x J 2 1 8 y J 2 1 8 x J 3

\ 8 w I ( 8 w I \ 8 w I

⁺ ^P 1,17 I I ⁺ ^P 1,22 ^w 4 ⁺ ^P 1,23 I I ⁺ ^P 1,24 I I ;

, 18 y J 3 , , 18 x J 4 , 18 y J 4

8 w ( 8 w I ( 8 w I

— = P 21 w 1 ⁺ P 22 I I ⁺ P 23 I 7- I ⁺ P 28 w 2 ⁺

8 x 18 x J 1 18 y J 1

( 8 w I ( 8 w I ( 8 w I

⁺ ^P 29 I I ⁺ ^P 2,10 I I ⁺ ^P 2,15 ^w 3 ⁺ ^P 2,16 I 77 I ⁺

18 x J 2 18 y J 2 18 x J 3

( 8 w I ( 8 w I ( 8 w I

⁺ ^P 2,17 I 77 I ⁺ ^P 2,22 ^w 4 ⁺ ^P 2,23 I 77 I ⁺ ^P 2,24 I 77 I ;

, 18 y J ₃ , , 18 x J 4 , 18 y J 4

д w (д w ) ( д w )

— = p31 w + p32 I I + p33 I I + p38 w + дy Vdx J V дy J1

⁺ p 39 ⁽£ J 2 ⁺ p «О ^ ) 2 ⁺ p «5 w 3 ⁺ p ^1J6 ⁽£ ) , + ^

+ P 3,17

( д w ) 1 ^д y J 3

+ P 3,22 ^W 4 + P 3,23

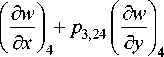
2 xy 3 x ² y 3 x ² 2 x

p 29 = k 2, ⁺ 2

ab a ² b a ² a

23 2 y ² y ³ y

^; ^p 2,10=" ⁺ аь ^ ⁺ a

6 x ² y 6 xy

p 2,15 = 3k ⁺ 27

ab ab

y 3 y ² 2 y ³

1 ;

ab ab ² b ³ a

2 xy 3 x ² y

^p 2,16 = k ⁺ 2, ;

ab a ² b

23 yy ³

p 2,17 = k ⁺ z.2 ;

ab ab ²

V x = ^p 44 V x 1 + ^p 4,11 V x 2 + p 4,18 V x 3 + p 4,25 V x 4 ;

6 x ² y 6 xyy 3 y ² 2 y ³

v y = p 55 V y 1 + p 5,12 V y 2 + p 5,19 V y 3 + p 5,26 V y 4 ;

u = ^p 66 ^u 1 + ^p 6,13 ^u 2 + ^p 6,20 ^u 3 + ^p 6,27 ^u 4 ^;

V = p77 у + p7,14 V2 + p7,21 V3 + p7,2gV4 , где pij – компоненты матрицы преобразования P размерностью 7x28 со следующими ненулевыми компонентами:

p 2,22 = з₇ 2 т ⁺ к z2 + i3 ^;

a ³ b a ² b ab ab ² b ³ a

p 2,23

= 4 xy ab

+ 3^ + y a ² b b

y ²

; p²²⁴ = ab

y 3 ; ab ²

p 31 ="

6 xy ² b ³ a

x 3 x ² 1

ab a ² b

2 x ³ 6 y 6 y ² a ³ b b ² b ³

6 xy ab ²

p ₁₁	= 1 - ^x y ₊ ³ ^x ² y ₊ ³ xy ² ab a ² b ab ²	2 x ³ y
p ₁₁	= 1 - ^x y ₊ ³ ^x ² y ₊ ³ xy ² ab a ² b ab ²	a 3 b
_-	2 xy ³ 3 x ² 3 y ² 2 x ³ b ³ a a ² b ² ⁺ a ³	+ 2 y 3 ; b ³
p ₁₂	= 2 x ² y x ³ y xy + x ³ ab a ² b b a ²	2 x ² + x a

2 x ² x ³ x p 32 = 7 27-Т^;

ab a ² b b

2 xy ² xy ³

^p 13 = к

ab ab ²

2 y ² xy y ³

"T" ⁺--T2"⁺ ^y ^;

b a b ²

p ₁₈

= xy + 3 x ² y 3 xy ² + ab a ² b ab ²

2 x ³ y 2 xy ³ 3 x ² 2 x ³

3 ⁺ 3 ⁺ 2 3 ;

a ³ b b ³ a a ² a ³

p 19 =■

2332

x y x y + x x ; ab a ² b a ² a

2 xyxyxy p 1,10 = 1 ⁺ ₂+ ;

ab ab ² a

xy 3 x ² y

^p 1,15 = k ⁺ 2, ⁺

ab a ² b

3 xy ² 2 x ³ y 2 xy ³

233 ;

ab ² a ³ b b ³ a

x ² y x ³ y

p 1,16 = —t⁺^t ;

ab a ² b

xy ² xy ³

^p 1,17 = Г ^{+ —};

ab ab ²

p 1,22

= xy 3 x ² y 3 xy ² + ab a ² b ab ²

2 x ³ y 2 xy ³ 3 y ² 2 y ³ ; a ³ b b ³ a b ² b ³

2 x yxyxy

p i ₂₃ =-- + + —+ + —

^, ab a ² b b

23 2 y ² y ³ y

; ^p 23 = , ,₂ ;

ab ab ² a

xy ²

^p 1,24 ^-—Г- ab

3 2 3

xy ³ y ² y ³

Г + ; ⁽¹³⁾

ab ² b b ²

6 x ² y 6 xyy

p 21 = 3 7 ⁺ 2 7 l

a ³ b a ² b ab

3 y ² 2 y ³ 6 x 6 x ²

⁺ 2 3 2 ⁺ 3 ;

ab ² b ³ a a ² a ³

4 xy 3 x

p 22 = ^{1 +} к 2

ab a ²

² y 3 x ² 4 x y ; b a ² a b ^;

6 x ² y 6 xyy p 28 = 2 _L⁺

a ³ b a ² b ab

3 y ² 2 y ³ 6 x 6 x ²

-- —1---1 ---‘

2 3 2 3 ⁵

ab ² b ³ a a ² a ³

p 33 =	. 1+4 xy ab	3 xy ² 3 y ² x 4 y z—i—z-----; ab ² b ² a b
p 38 =	₌6 xy ^+ b ³ a	x 3 x ² + 2 x ³ 6 xy ; ab a ² b a ³ b ab ²
x ² p 39 ^=—7 ab	x ³ a ² b ^;	4 xy 3 xy ² x ^p 3,10 =-- Г ^{+ —}ГТ + ^- ab ab ² a
^p 3,15 =	6 xy ² b 3 a	x + 3 x ² 2 x ³ + 6 xy ; ab a ² b a ³ b ab ² ^;
p 3,16 = ^-	x ² x ³ 2 xy 3 xy ² + ; p 3 17 =+ ab a ² b ^, ab ab ²

6xy2 x 3x2 2x3 6y 6y26

^p “2 = b^ + aTTb ⁺ ab ⁺¥" b ^;

2x2 x3

^p 3,23 =--/ ' ⁺ "k ;

aba

2xy 3xy2 3y2 2yxyxy p3,24 + ; p44 = 1 + ab ab2b2b ab a b xyx xy xyy p4,11 = T + — ; p4,18 = "T; p4,25 = Г + Т ;

ab a ab ab b

xyxy p 55 = ¹ ⁺ A^---? ; ab a b

xyx p 5,12 = 7 + — ;

ab a

xy xyy p5,19 = "T ; p5,26 = Г + T ;

ab ab b

xyxy ^p 66 = ¹ ^{+ —}й — 7 ^; ab a b

xyx p6,13 = 7 + “ ;

ab a

xy xyy p6,20 = "Г ; p6,27 = 7 + T ;

ab ab b

xyxy p 77 = 1 +~7* ab a

xyx p 7,14 = 7 + — ;

ab a

xy xyy p721 = ab; p7,28=-ab+b •

Подставляя разложения (12) в выражения потенциальной энергии деформации (7) и потенциала внешних сил (8) и минимизируя их сумму (9) по компонентам вектора узловых кинематических параметров δ е (10), (11), получим систему алгебраических уравнений равновесия

K e δ e = F e , (14)

где Ke – матрица жесткости конечного элемента цилиндрической оболочки; Fe – вектор эквивалентных узловых сил.

Вектор эквивалентных узловых сил удобно представить в блочном виде:

F e

F 1

F 2

F 3 . F4

где подвекторы F 1 , F 2 , F 3 , F 4 , состоящие из 7 компонентов каждый (в случае нагрузки равномерным давлением) имеют вид

F = { f , f, f , 0 0 0 0 } Т ;

F2 ={ f8 f9 f.0 0 0 0 0}Т ;(16)

F3 ={f 5 fi6 f7 0 0 00

F4 ={ f22 f23 f,4 0 0 00

ab a2b ab2 ab fi = p T; f2 = p —; f, = p —; f8 = p T;

a2b ab2 ab f9 =- p “24; f10 = p “24; f.5 = p “4“;

a2b ab2 ab f16 =- p "24; f.7 =- p ""24; f22 = p ”4-’ a2b ab2

^f ²³ = p 24 ; ^f ²⁴ = p 24 .

Здесь p – величина давления.

В общем случае матрица жесткости конечного элемента цилиндрической оболочки K _e , размерность которой 28 x 28, имеет плотное заполнение, т. е. в ней немного нулевых элементов. Для ее вывода разработана специальная программа [2].

Вывод разрешающих уравнений при реализации вариационного подхода МКЭ для оболочек предполагает получение выражения полной потенциальной энергии для всего ансамбля конечных элементов модели:

E ^ =^ L ( U + П? ) , (17)

i = 1

где N – число элементов в модели; U_i – потенциальная энергия деформации i -го элемента; П i – потенциал внешних сил i -го элемента.

Минимизация (17) по узловым неизвестным каждого узла системы приведет к глобальным уравнениям равновесия

K Σ Δ = F Σ , (18)

где K Σ – глобальная матрица жесткости пластины; F_Σ – глобальный вектор эквивалентных узловых сил всей пластины; Δ – глобальный вектор узловых неизвестных:

Δ = { δ 1 δ 2 … δ i … δ N } ^Т . (19)

Следует иметь в виду, что при решении СЛАУ (18) необходимо учесть граничные условия.

Одной из самых распространенных конструкций, в расчетах которых необходимо учитывать трансверсальный сдвиг, является трехслойная оболочка с податливым заполнителем. Будем полагать, что жесткость несущих слоев существенно выше жесткости промежуточного слоя. В этом случае можно допустить, что параметры жесткости оболочки B , C и D обеспечены несущими слоями.

Будем полагать материалы несущих слоев и заполнителя изотропными. При совпадении начальной поверхности со срединной и при симметричной структуре слоистого пакета смешанные жесткости ( C ) равны нулю. Остальные параметры жесткости вычисляются по формулам

2 E н t

B 11 = B 22 = ₁ 2 ,

1 -о Н

B 12 = B 21 = 0 н B 11 ,

B 33 = 2 G H t ,

D -D ~ EH ( H 3 - h ³)

D ¹¹ = D ²² = 12(1 -о н ) •

D 12 = D 21 = ⁰ н D 11 ,

D = G h ( H ³ - h ³)

³³ 12(1 -о Н )

H ²

2 th ^, 1

GG нз

где H – полная толщина пакета; h – толщина слоя заполнителя; t – толщина каждого из несущих слоев; E н – приведенный модуль упругости материала несущих слоев; G н и G з – модули сдвига материалов несущих слоев и заполнителя соответственно.

Как известно, в последнее время получила распространение конечно-элементная модель податливых при трансверсальном сдвиге оболочек, в которой в качестве основных узловых переменных фигурируют перемещения точек начальной поверхности и углы поворота сечения (θ x и θ y ). Эта модель с пятью кинематическими параметрами в узле обладает определенным недостатком, который называется эффектом сдвигового запирания (ЭСЗ).

Покажем, что наша КЭ модель с семью кинематическими параметрами в каждом узле лишена данного недостатка. Для этого проведем следующий численный эксперимент. Выполним две серии расчетов для оболочек различной толщины. В первой серии будет задействована рассматриваемая в настоящей работе модель с 7 узловыми кинематическими параметрами.

Во второй серии будем использовать конечно-элементную модель, основывающуюся на классической теории оболочек Кирхгофа. В этой классической модели в каждом узле присутствует 5 кинематических переменных: перемещения u и v , прогиб w и два изгибных угла поворота нормали ( dw/dx и dw/dy ). Таким образом, вектор узловых неизвестных 4-узлового элемента оболочки в данном случае будет иметь вид (10) со следующим подвектором узловых параметров в каждом узле:

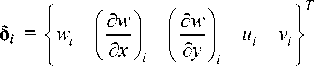
Процедура вывода разрешающих уравнений равновесия для одного конечного элемента точно такая же, что описана выше для модели, учитывающей трансверсальный сдвиг. Только во всех выражениях необходимо положить ψ x = ψ y = 0 и, следовательно, θ x = – dw/dx и θ y = – dw/dy.

Выражение энергии деформации при этом будет иметь вид

ленного композита с углами укладки φ = ±45°. Зададим следующие механические свойства (углепластик):

– модуль упругости вдоль волокон E ₁ = 180 ГПа;

– модуль упругости поперек волокон E 2 = 6,2 ГПа;

– модуль сдвига G 12 = 5 ГПа;

– коэффициент Пуассона μ 12 = 0,007;

– плотность ρ = 1500 кг/м3.

Упругие параметры пластины, которую будем считать однослойной и условно однородной, вычислим по формулам

A ₁₁ = E₁ cos ⁴ ф + E ₂ sin ⁴ ф +

+ 2 ( Е 1 Ц 12 + 2 G 12 ) sin ² ф cos ² ф ;

A ₂₂ = E 1 sin ⁴ ф + E ₂ cos⁴ ф + + 2 ( Е 1 ц ₁₂ + 2 G ₁₂ ) sin ² ф cos ² ф ;

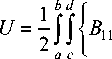
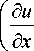
+ ^D11

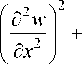
A 12 = A 21 = E 1 H 12 ⁺

⁺ ( E 1 ⁺ E 2 - ² ( E 1 ^ 12 ^{+ 2} G 12 ) ) sin ² ф cos ² ф ;

A 33 = ( E 1 + E 2 — 2 Ё 1 Ц 12 ) sin ² ф cos ² ф + G ₁₂ cos ² 2 ф ,

8 u (8 v w |

+ 2 B + + 2 D i ₂

¹² 8 x (8 y R J ¹²

8 ² w || 1 8 v 8 ² w ^^^^^^^^^^^^^^^^^^^^^^^_— I I ^^^^^^^^^^* ^^^^^^^^^^^^^^* ^^^^^^* ^^^^^^^^^^^^^^^^^^^^^^^* 8 x ^{2 J} ( R 8 y 8 y ²

где E ₁ и E ₂ – приведенные модули упругости, вычисляемые по формулам

(8v w | ( 8Vy 1 8v8

+ B22 I + I + D22 +—

(8y R) (8y R 8y

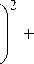
E 1(2) = E 1(2) /⁽¹ ^ 12 ^ 21 ) ,

а коэффициент Пуассона μ 21 определяется из условия симметрии упругих постоянных:

( 8 u , 8v Y

+ B 33 1--+--I + D 33

(8 y 8 x )

1 8 v 2 8 2 w

R 8 x 8 x 8 y

- dxdy .

^ 21 =

^-12 ^E 1

Размерность матрицы жесткости элемента сократится до 20. Вектор эквивалентных узловых сил сохранит блочный вид (15), но подвекторы (16) будут иметь размерность 5 с теми же значениями ненулевых компонентов.

Рассмотрим цилиндрическую панель, с защемленными торцевыми (искривленными) кромками и свободными прямыми (см. рисунок), нагруженную равномерным давлением на внешней поверхности. Радиус кривизны панели – 5 м. Размеры в плане 1 м на 1 м. Будем полагать оболочку изготовленной из однонаправ-

Модули трансверсального сдвига примем равными G 12 .

Коэффициенты жесткости пластины вычислим по формулам

^B 11 = A 11 h ; ^B 22 = A 22 h ; ^B 21 = A 21 h ;

A ₁₁ h ³ A ₂₂ h

^B 33 = A 33 h ; D 11 = 12 ; D 22 = 12

A 12 h ³	A 21 h ³	A ₃₃ h ³
D ¹² 12 ;	D ²¹ 12	; D³³ 12

K x = K y = G 12 h .

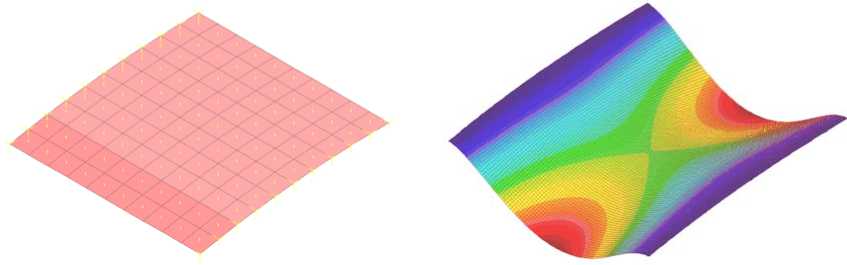
Композитная панель и картина деформирования

Таблица 1

Прогибы однородной композитной панели

Толщина оболочки, h , мм	Прогиб в центральном узле, мм		Расхождение, %	Давление, Па
Толщина оболочки, h , мм	Классическая модель	Модель, учитывающая сдвиг	Расхождение, %	Давление, Па
50	4,593	5,070	9,4	1000000
40	8,579	9,144	6,18	1000000
30	18,566	19,219	3,40	1000000
20	4,993	5,055	1,23	100000
10	1,7817	1,7811	0,034	10000
5	2,8689	2,8619	0,24	10000
1	–0,522263	–0,522286	0,0044	100

Таблица 2

Прогибы трехслойной панели

Толщина слоя заполнителя, h , мм	Прогиб в центральном узле, мм		Расхождение, %	Давление, Па
Толщина слоя заполнителя, h , мм	Классическая модель	Модель, учитывающая сдвиг	Расхождение, %	Давление, Па
50	4,718	10,717	55,98	100000
40	7,302	14,673	50,24	100000
30	6,369	11,119	42,72	50000
20	2,778	4,117	32,52	10000
10	4,990	6,101	18,21	5000
5	1,610	1,765	8,78	500
3	0,675	0,708	4,66	100
1	2,02	2,045	1,22	100
0,5	1,4358	1,4444	0,595	50
0,1	0,39015	0,39065	0,128	10

Определим прогибы в центральном узле, вычисляемые по классической (Кирхгофа–Лява) и сдвиговой моделям для различных значений толщины панели. Результаты расчетов представим таблично (табл. 1). Анализ этих данных позволяет заключить, что по мере увеличения толщины оболочки классическое решение дает существенно заниженный прогиб. С другой стороны, по мере уменьшения толщины пакета решение по сдвиговой модели приближается к классическому.

Еще более рельефно отмеченные эффекты проявляются в расчетах по классической и сдвиговой моделям, выполненным для трехслойной панели. Длина панели (по образующей – 1 м, ширина (в окружном направлении) – 0,2 м. Радиус кривизны – 5 м. Толщина стальных несущих слоев – 1 мм, толщина слоя заполнителя варьируется. Коэффициенты жесткости вычисляются по формулам (21).

С помощью специально разработанной программы [3] выполнена серия статических расчетов панели при нагрузке давлением. При этом оцениваются прогибы в центральном узле, полученные для трехслойной оболочки с различной толщиной слоя заполнителя. Параллельно выполняются расчеты по двух КЭ моделям: сдвиговой и без учета сдвига (Кирхгофа–Лява). Результаты представлены таблично (табл. 2). Данные таблицы показывают, что по мере уменьшения толщины слоя заполнителя результаты решения с использованием сдвиговой модели приближаются к ре- зультатам, полученным на основе классического решения, что свидетельствует об отсутствии ЭСЗ в разработанной КЭ модели. Эти же результаты лишний раз подчеркивают необходимость применения сдвиговой модели для расчета конструкций, весьма податливых при трансверсальном сдвиге.

Разработана конечно-элементная модель цилиндрической оболочки, податливой при трансверсальном сдвиге. Разрешающие уравнения теории МКЭ получены вариационным способом. Вектор узловых неизвестных содержит семь независимых кинематических параметров, включая осредненные по высоте сечения углы трансверсального сдвига. В результате численного эксперимента на примерах расчетов монолитной композитной и трехслойной оболочек показано, что в КЭ модели с полным набором узловых кинематических параметров отсутствует эффект сдвигового запирания.

Статья научная