Конечно-элементный расчет эллиптического цилиндра в геометрически нелинейной постановке при использовании векторной формы интерполяционной процедуры
Автор: Клочков Ю.В., Джабраилов А.Ш., Ищанов Т.Р., Марченко С.С., Андреев А.С., Клочков М.Ю.
Статья в выпуске: 1, 2022 года.
Бесплатный доступ
Изложен разработанный алгоритм вычисления прочностных параметров тонкой оболочки в виде эллиптического цилиндра с учетом сдвиговых деформаций в геометрически нелинейной постановке. В качестве инструмента исследования был использован численный метод конечных элементов (МКЭ). Разработан алгоритм формирования матрицы жесткости и столбца узловых усилий на шаге нагружения при использовании двух вариантов интерполяционной процедуры. В первом варианте была реализована стандартная для МКЭ интерполяция отдельных компонент шагового вектора перемещения и компонент шагового вектора углов поворота нормали через узловые значения соответствующих компонент. Во втором варианте была использована разработанная векторная форма интерполяционной процедуры, при которой интерполяционное выражение было записано непосредственно для вектора шагового перемещения и шагового вектора углов поворота нормали. В результате реализации векторной формы интерполяционной процедуры были получены альтернативные стандартным интерполяционные выражения, содержащие параметры используемой криволинейной системы координат. Элементом дискретизации эллиптического цилиндра был выбран четырехузловой фрагмент срединной поверхности с узловыми варьируемыми параметрами в виде компонент шагового вектора перемещения, их первых производных, а также компонент шагового вектора углов поворота нормали. На примере расчета эллиптического цилиндра в геометрически нелинейной постановке, загруженного в середине пролета сосредоточенной силой, был выполнен сравнительный анализ двух вариантов интерполяционной процедуры. Показано, что при расчете эллиптических цилиндров в криволинейной системе координат в геометрически нелинейной постановке необходимо применить разработанную векторную форму интерполяционной процедуры. Использование стандартной для МКЭ формы интерполяции искомых неизвестных позволило получать корректные результаты лишь в случае кругового цилиндра.
Метод конечных элементов, четырехузловой элемент, векторная интерполяция, геометрическая нелинейность
Короткий адрес: https://sciup.org/146282439
IDR: 146282439 | УДК: 539.3
Текст научной статьи Конечно-элементный расчет эллиптического цилиндра в геометрически нелинейной постановке при использовании векторной формы интерполяционной процедуры
ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2022PNRPU MECHANICS BULLETIN
Конструктивные элементы из эллиптических цилиндров являются неотъемлемой частью многих тех-носферных объектов промышленного и гражданского назначения. Определение прочностных параметров эллиптических цилиндров, особенно в геометрически нелинейной постановке, в настоящее время осуществляется посредством численных методов расчета [1–7], наиболее распространенным из которых является метод конечных элементов (МКЭ) [8–14]. При разработке конечно-элементных алгоритмов расчета эллиптических цилиндров исследователям неизбежно приходится решать вопрос о реализации интерполяционной процедуры, являющейся по своей сути фундаментальным аспектом МКЭ.
Если в качестве глобальных координат при расчете эллиптических цилиндров выбрать «естественные» криволинейные координаты, связанные с параметрами срединной поверхности оболочки данного типа, то необходимо использовать векторную форму интерполяционной процедуры [15; 16].
В изложенной работе представлен алгоритм расчета прочности эллиптического цилиндра в геометрически нелинейной постановке с учетом деформаций сдвига при реализации векторной формы интерполяции искомых величин.
1. Материалы и методы
Положение точки срединной поверхности эллиптического цилиндра можно задать радиус-вектором
Ro = xi + r (ф)-sin (ф) j + r (ф)-cos (ф) k, (1)
где i , j , k - орты декартовой системы координат; ф -полярный угол эллипса, являющегося поперечным сечением эллиптического цилиндра плоскостью, перпендикулярной продольной оси ОХ цилиндра.
Полярный радиус поперечного сечения эллиптического цилиндра определяется следующей зависимостью r (ф) = ab / a 2cos2ф + b 2sin2ф.
Выражения для ортов локального базиса точки срединной поверхности эллиптического цилиндра могут быть получены с использованием формулы дифференциальной геометрии e0 = R0x; e = R0ф-(дф/d-); e0„ = e0xe02, (2)
где s – длина дуги эллипса поперечного сечения эллиптического цилиндра с параметрами a и b .
Из (2) можно получить прямую и обратную матричные зависимости
{ e " } = [ d 0 ]№ { i } = [ d " ] - 1 { e " } , (3)
где { e 0 } T = { e " e 2 e n } ; { i ) T = { ijk ) .
Положение точки M " z , расположенной в произвольном слое эллиптического цилиндра, находящегося на расстоянии t от срединной поверхности, в недеформирован-ном состоянии определяется радиус-вектором
R " t = R " + 1 e " . (4)
После серии последовательных шагов нагружения точки M 0 и M 0 t переместятся в положения M и Mt , которые могут быть определены соответствующими радиус-векторами
R = R 0 + v ; R t = R 0 t + V , (5)
где v и V – суммарные векторы перемещения точек M 0 и M 0 t за j шагов нагружения.
После завершения ( j +1)-го шага нагружения точки M и Mt перейдут в точки M * и M * t , положения которых могут быть определены посредством радиус-векторов
R * = R + w ; R * t = R t + W , (6)
где w и W – векторы шаговых перемещений точек M и Mt .
Входящие в (5) и (6) суммарный и шаговый векторы перемещения точки M 0 t определяются по формулам
V = v + t y ; W = w + 1 A y , (7)
где y и Ay - суммарный и шаговый векторы углов наклона нормали y = у™e; Ay = Ay™e, (8)
где индексы а последовательно принимают значения 1 и 2.
Выполняя операцию дифференцирования (5) и (6), можно получить выражения для векторов базиса в точке произвольного слоя эллиптического цилиндра после j шагов нагружения и на ( j +1)-м шаге
-
g . R t в ; g 3 = R ; g ^ = R /. ; g 3 = R * t , (9)
где индекс в принимает значения x и ф .
Приращение деформаций в произвольном слое эллиптического цилиндра на ( j +1)-м шаге нагружения можно получить, используя соотношение механики сплошных сред [17]
Ae tm„ = ( g*m„ — g m„ ) /2, (10)
где g mn = g m • g n ; g mn = g ' m " д П •
Поверхность эллиптического цилиндра моделируется совокупностью четырехузловых элементов дискретизации, ориентированных вдоль линий главных кривизн. Узловыми варьируемыми параметрами дискретного элемента являются компоненты вектора шагового перемещения точки срединной поверхности, первые производные этих компонент и компоненты шагового вектора углов поворота нормали. Столбцы искомых узловых неизвестных в глобальной x , ф и локальной — 1 < Z , П ^ 1 системах координат могут быть представлены в следующем матричном виде
{ A U G } T = ( { A u G } T { A vG } T { A wG } T { Ay 1 } T { Ay 2 } T } ; (11)
1 x 44 I 1 x 12 1 x 12 1 x 12 1 x 4 1 x 4 J
{AUL}T = ({AuL}T {AvL}T {AwL}T {Ay1}T {Ay2}T}, (12) 1x44 I 1x12 1x12 1x12 1x4 1x4 J где {AqG}T = {Aq* AqjAqkAq1 Aq‘x „.Aq‘xAq^ „.Aq^};
1 x 12
{ a qL } T = { a q‘ A qj A qk A q1 A q , z „ A q ^A q ^ „ A q ^ } ; 1 x 12
{ Aya } T = { Aya i Aya j Aya k Aya 1 } • 1 x 4
Здесь под A q понимается компонента вектора шагового перемещения A u , A v и A w .
w = A u e " + A v e 2 +A w e n . (13)
В настоящей статье при построении интерполяционных выражений реализованы два варианта. В первом варианте применялся общепринятый в МКЭ подход [18–25], при котором каждая компонента вектора шагового перемещения A q и каждая компонента шагового вектора углов поворота нормали Ay ™ интерполируются через узловые значения своей же компоненты
A q = { v } T { A qL } ; Ay “ = { x } T { Ay ™ } . (14)
Входящие в (14) функции формы {ф}T и {х}T представляют собой произведения полиномов Эрмита третьей степени и билинейные функции локальных координат Z, П соответственно. Использование стандартной интерполяционной процедуры (14) оправдано при решении задач в прямоугольной декартовой системе координат. Однако при исследовании НДС тел, имеющих криволинейные очертания (к которым относятся оболочки вообще и эллиптические цилиндры в частности) целесообразнее применять криволинейные системы координат (цилиндрические, сферические, тороидальные), специально разработанные для анализа объектов с криволинейными границами. На криволинейной поверхности локальный базис постоянно изменяется при переходе от точки к точке, поэтому интер- поляционные выражения должны содержать параметры используемой системы криволинейных координат. Такому критерию удовлетворяет векторная форма интерполяционной процедуры, которая и была реализована во втором варианте расчёта. Узловыми варьируемыми параметрами при этом выбираются непосредственно векторы шагового перемещения, первые производные этих векторов и шаговые векторы углов поворота нормали
{wG } ={w1 wjw*wlwix--wlxw^^wl ф);(15)
1 X 12
{wL } ={wiw jwkw1 wi^^wl, ^w,n.w1яЬ
1 X 12
{Ay}t ={ay' Ay j Ay*Ay 1}.(17)
1 x 4
Применяя интерполяционные выражения (14) к векторным узловым неизвестным, можно записать следующие интерполяционные зависимости w = {vjT {wL} = {vjT [L]{wG } = {X}T {wG };
1 X 12 12 x 1 1 X 12 12 x 12 12 x 1 1 x 12 12 x 1
AY ={x} T {AY},
1x44
где [ L ] - матрица перехода от (16) к (15). 12 x 12
Входящие в (18) и (19) узловые векторы шагового перемещения, а также первые производные этих векторов по криволинейным координатам x и ф, шаговые векторы углов поворота нормали могут быть представлены компонентами узловых векторов локального базиса wp = au pe0p + av pe0p + Aw pe0p; wp = zxlpe"p + z pe0p;
12 П , X X a
< = z ( ■ zфe0„p;
Ay p= AY1pe0p + Ay 2pe2p, где верхний индекс p обозначает узлы конечного элемента i, j, k, l.
Соотношения (18) и (19) с учётом (20), (21) запишутся следующим образом w = {X}T [ Aw]{nw}; (22)
1 X 12 12 x 36 36 x 1
A y = { x } T [ A у ] { « Y } , (23)
1 X 4 4 x 8 8 X 1
Элементами квазидиагональных матриц [ A w ] и 12 x 36
[ A y ] являются соответствующие матрицы-строки, со- 4 x 8
держащие узловые векторы локального базиса
{eWP}T ={e0pe2pe0P}; {e0p}T = {e0pe0p}.(24)
1x31
Матрицы (24) на основании (2) могут быть выражены через орты декартовой системы координат
{cWp} = [d0p]{i}; {eYp} = [b0p ]{i}.(25)
3 x 1 3 x 3 3 x 1 2 x 1 2 x 3 3 x 1
С учётом (3) матричные выражения (25) примут вид ew [ d -][ d"] e [ с » ]{e"};
3 x 1 3 x 3 3 x 3 3 x 1 3 x 3 3 x 1
№ [ b0 p ][ d 0 ] - 1 { e 0 } = [ t0 p ] { e 0 } . (26)
2 X 1 2 x 3 3 x 3 3 x 1 2 x 3 3 x 1
Представляя вектор шагового перемещения w и шаговый вектор углов поворота нормали Δ γ компонентами локального базиса точки внутренней области конечного элемента и учитывая (26), интерполяционные выражения (22), (23) могут быть записаны в виде
{ e 0 } T { w } = 1 x 3 3 x 1
= { e 0 } T [X 1 [ c" ■ ] T | X 2 [ c 0 j ] T |X , [ c" * ] T |X 4 [ c 0 1 ] T | X , [ 1v3 [ I I I I
1 x 3
Jx , [ c 0 1 ] T k, [ c 0 i ] T Ik12 [ c 0 1 ] T 1 { n w } ;
1 1 I 1 ] 36 x 1
{ e ; } T { A y } = 1 x 2 2 x 1
36 x 1
c 0 i
] 1.
= { e 0 } T [x . [ t1 i ] T |X 2 [ t 0 j ] T |X 3 [ t 0 * ] T |X 4 [ t11 ] T П{ n , } . (28) 1x2 L 1 1 1 U 8x1
где { w } T = { A u A v A w } ; { A y } T = { a Y A Y 2 } ; { e Y } = { e 10 e 2 } . 1 x 3 1 x 2 1 x 2
Из сопоставительного анализа левых и правых частей (27) и (28) можно получить интерполяционные выражения для компонент вектора шагового перемещения и компонент шагового вектора углов поворота нормали
0 i 0 i 0 i 0 j 0 j 0 j 0 k 0 k 0 k
A u { X 1 { С11 с 21 с 31}| X 2 { С11 с 21 с 31 }| X 3 { С11 с 21 с 31 }|
0 l 0 l 0 l с 11 с 21 с 31
}|х , { с с с ;}| •••
где { n w } T = { A u i A v i A w A uj A vj A wj A uk A v * A w * A u1 A v l A w l 1 x 36
.|х , { с“с 2~ с 01}| х , { с 01 с 21 с з"1}| .|Х 12 { с Ц с” с " }} { п. } ;
J 36 x 1
1i2ii l1i2ii l z z z z z z z z k xxx x ф ф ф ф J ’
a v = { Х 1 { с 12 с 22 с 02 }| .^ 12 { с 02 с 02 с 02 } } { « ^ } ;
36 x 1
{ n y ) T = { Y 1 i Y 2 ' Y 1 j Y 2 j Y 1 * Y 2 * Y 1 1 Y 2 1 } • 1 x 8
A w = { Х 1 { с-с 203 с ,'; } |.|Х 12 { с 03 с 0 с ,'3 } } { п , } ; L J 36x1
10 i 0 i 0 j 0 j 0 k 0 k 0 l 0 l
Л у = { X 1 { t 11 t 21}| X 2 { t 11 t 21 }| X 3 { t 11 t 21 }|X 4 { t 11 t 21 } } { n Y }
8 x 1
20 i 0 i 0 j 0 j 0 k 0 k 0 l 0 l
Л у = { X 1 { t 12 t 22 j| X 2 { t 12 t 22 }| X 3 { t12 t 22 j| X 4 { t12 t 22 }}{ n y } - (29) 8 x 1
Интерполяционные зависимости в варианте стандартной для МКЭ (14) процедуры или в варианте новой (29) векторной формы интерполяции искомых величин позволяют скомпоновать следующее матричное соотношение
{де m, } = [ B ]{A UG }, (30)
5 x 1 5 x 44 44 x 1
где { Л е m, } Г = { A E t ^E t 2 2А е ^ з Л е 22 2Л е 2з } .
1 x 5
Матрица жесткости и столбец узловых усилий конечного элемента на ( j +1)-м шаге нагружения компонуются путём минимизации функционала Лагранжа согласно стандартной для МКЭ в форме метода перемещений процедуре [26–35].
2. Пример расчета 1
Была решена задача по исследованию НДС цилиндрической оболочки, загруженной в середине пролёта сосредоточенной силой P и имеющей на диаметрально противоположной стороне шарнирную опору, препятствующую вертикальному смещению. По торцам оболочка имела скользящую заделку. Вследствие наличия плоскостей симметрии была рассчитана 1/4 часть цилиндра. Расчетная схема конструкции представлена на рис. 1. Были приняты следующие исходные данные: P = 453,6 H ; E = 0,738• 105 МПа; v = 0,3125; h = 2,4 • 10 - 3 м; длина образующей L = 26,29 • 10 - 2 м. Первоначально параметры эллипса поперечного сечения цилиндрической оболочки принимались одинаковыми a = b = 12,58 • 10 - 2 м, т.е. цилиндр был круговым.
Расчёты были выполнены в двух вариантах: в первом варианте при формировании матрицы жесткости и столбца узловых усилий конечного элемента на шаге нагружения была использована стандартная для МКЭ интерполяционная процедура (14); во втором варианте для интерполяции компонент вектора шагового перемещения и шагового вектора углов поворота нормали была применена разработанная векторная форма интерполяции искомых величин (29).
Результаты повариантного расчёта кругового а = b цилиндра представлены в табл. 1, в которой приведены численные значения нормальных и сдвиговых напряжений на внутренней О в и наружной С н поверхностях оболочки на торце цилиндра в точках A ( L /2; 0.0 ) и B ( L /2; п ) , а также значение прогиба в точке приложения силы P ( 0.0;0.0 ) в зависимости от густоты сетки дискретизации оболочки при фиксированном числе шагов нагружения, равном 30.
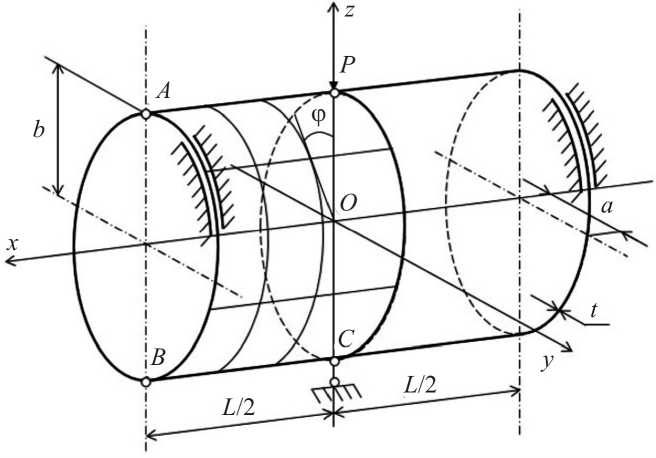
Рис. 1. Расчетная схема эллиптического цилиндра, загруженного сосредоточенной силой P
Fig. 1. Design diagram of an elliptical cylinder loaded with a concentrated force P
Анализ данных табл. 1 показывает, что в обоих вариантах расчета кругового цилиндра наблюдается устойчивая сходимость вычислительного процесса по мере сгущения сетки дискретизации. Контролируемые параметры НДС кругового цилиндра в точках А и В (которые должны быть одинаковыми, исходя из симметрии расчетной схемы) практически совпадают и в первом, и во втором вариантах расчета. Различия между вариантами расчета пренебрежимо малы.
В табл. 2 представлены повариантные значения напряжений и прогиба под сосредоточенной силой в концевом и срединном сечениях кругового цилиндра в зависимости от количества шагов последовательного нагружения при фиксированной сетке дискретизации рассчитываемого фрагмента оболочки 25 x 25 узлов. Анализ данных табл. 2 позволил сделать вывод об устойчивой сходимости вычислительного процесса с увеличением количества шагов нагружения в обоих вариантах расчета. Также можно отметить, что при расчете кругового цилиндра в обоих вариантах расчета наблюдаются практическое совпадение значений напряжений в точках А, В и Р, С соответственно, чего и следовало ожидать, учитывая наличие вертикальной плоскости симметрии расчетной схемы.
Результаты расчётов позволяют сделать вывод, что при анализе НДС кругового цилиндра в геометрически нелинейной постановке оба варианта интерполяционной процедуры дают практически одинаковые значения параметров НДС оболочки.
3. Пример расчета 2
Рассмотрим задачу исследования НДС эллиптического цилиндра, расчётная схема которого совпадает с круговым цилиндром из примера 1. Соотношение параметров эллипса поперечного сечения эллиптического цилиндра примем равным а / b = 2 /1. Результаты пова-риантных расчётов представлены в табл. 3, структура которой идентична структуре табл. 1.
Анализируя данные табл. 3, можно отметить, что и в первом, и во втором вариантах расчета наблюдается сходимость вычислительного процесса со сгущением сетки дискретизации. Однако между вариантами расчета имеются принципиальные и весьма существенные различия. Так, в первом варианте расчета эллиптического цилиндра значения напряжений в точке В примерно в два раза меньше, чем в точке А, в то время как при расчете кругового цилиндра значения напряжений в данных точках практически совпадали. Причем сгущение сетки дискретизации не уменьшает погрешности вычислений по первому варианту. Значения прогиба под сосредоточенной силой в первом варианте также оказались заниженными в 1,67..1,61 раза по сравнению со вторым вариантом расчета. Во втором варианте расчета можно отметить полное совпадение значений напряжений, вычисленных в точках А и В, что и должно быть при выбранной расчетной схеме эллиптического цилиндра.
В табл. 4, структура которой совпадает с таковой табл. 2, можно отметить сходимость повариантных расчетов с увеличением количества шагов нагружения. Но, как и в табл. 3, можно констатировать существенные погрешности вычислений напряжений и прогиба в первом варианте расчета, как в концевом, так и в срединном сечениях эллиптического цилиндра.
Таблица 1 / Table 1
Численные значения нормальных и сдвиговых напряжений на внутренней σ в и наружней σ н поверхностях кругового цилиндра
Numerical values of normal and shear stresses on the inner σ в in and outer σ н n surfaces of a circular cylinder
|
Координаты точек x , ϕ (м, рад) |
Напряжения, МПа, прогиб, см |
Вариант интерполяционной процедуры |
|||||||
|
Скалярная |
Векторная |
||||||||
|
Сетка узлов |
|||||||||
|
21 × 21 |
24 × 24 |
26 × 26 |
28 × 28 |
21 × 21 |
24 × 24 |
26 × 26 |
28 × 28 |
||
|
т. А: x = L /2; ϕ= 0.0 |
σ в xx |
13,30 |
12,96 |
12,78 |
12,61 |
13,16 |
12,85 |
12,68 |
12,53 |
|
σ в θθ |
53,63 |
53,35 |
55,22 |
53,10 |
53,23 |
53,04 |
52,95 |
52,87 |
|
|
σ в xz |
–6,85 |
–7,64 |
–8,17 |
–8,70 |
–6,80 |
–7,60 |
–8,13 |
–8,67 |
|
|
σ н xx |
–12,87 |
–12,57 |
–12,40 |
–12,25 |
–12,74 |
–12,47 |
–12,32 |
–12,18 |
|
|
н σθθ |
–56,88 |
–56,97 |
–57,07 |
–57,17 |
–56,44 |
–56,48 |
–56,83 |
–56,96 |
|
|
σ н xz |
–6,85 |
–7,64 |
–8,17 |
–8,70 |
–6,80 |
–7,60 |
–8,13 |
–8,66 |
|
|
т. В: x = L /2; ϕ=π |
σ в xx |
13,29 |
12,96 |
12,77 |
12,61 |
13,16 |
12,85 |
12,68 |
12,53 |
|
в σθθ |
53,61 |
53,34 |
53,21 |
53,10 |
53,23 |
53,04 |
52,95 |
52,87 |
|
|
σ в xz |
–6,85 |
–7,64 |
–8,17 |
–8,70 |
–6,80 |
–7,60 |
–8,13 |
–8,67 |
|
|
σ н xx |
–12,88 |
–12,57 |
–12,41 |
–12,25 |
–12,74 |
–12,47 |
–12,32 |
–12,18 |
|
|
н σθθ |
–56,84 |
–56,98 |
–57,08 |
–57,17 |
–56,44 |
–56,68 |
–56,83 |
–56,96 |
|
|
σ н xz |
–6,85 |
–7,64 |
–8,17 |
–8,70 |
–6,80 |
–7,60 |
–8,13 |
–8,66 |
|
|
т. Р : x = 0.0; ϕ= 0.0 |
w |
–0,5717 |
–0,5748 |
–0,5763 |
–0,5776 |
–0,5738 |
–0,5764 |
–0,5777 |
–0,5787 |
Таблица 2 / Table2
Численные значения нормальных и сдвиговых напряжений на внутренней σ в и наружней σ н поверхностях кругового цилиндра
Numerical values of normal and shear stresses on the inner σ в in and outer σ н n surfaces of a circular cylinder
|
Координаты точек x , ϕ (м, рад) |
Напряжения, МПа, прогиб, см |
Вариант интерполяционной процедуры |
|||||
|
Скалярная |
Векторная |
||||||
|
Число шагов нагружения |
|||||||
|
20 |
30 |
50 |
20 |
30 |
50 |
||
|
т. А : x = L /2; ϕ= 0.0 |
σ в xx |
12,77 |
12,77 |
12,78 |
12,67 |
12,67 |
12,68 |
|
σ в θθ |
52,82 |
52,84 |
52,85 |
52,53 |
52,55 |
52,57 |
|
|
σ в xz |
–7,81 |
–7,81 |
–7,81 |
–7,77 |
–7,77 |
–7,77 |
|
|
σ н xx |
–12,39 |
–12,40 |
–12,40 |
–12,30 |
–12,31 |
–12,31 |
|
|
н σθθ |
–56,52 |
–56,54 |
–56,55 |
–56,26 |
–56,27 |
–56,29 |
|
|
σ н xz |
–7,81 |
–7,81 |
–7,81 |
–7,77 |
–7,77 |
–7,77 |
|
Окончание табл. 2
|
Координаты точек x , ϕ (м, рад) |
Напряжения, МПа, прогиб, см |
Вариант интерполяционной процедуры |
|||||
|
Скалярная |
Векторная |
||||||
|
Число шагов нагружения |
|||||||
|
20 |
30 |
50 |
20 |
30 |
50 |
||
|
12,76 |
12,77 |
12,77 |
12,67 |
12,68 |
12,68 |
||
|
σ в θθ |
52,81 |
52,83 |
52,84 |
52,53 |
52,55 |
52,57 |
|
|
σ в xz |
–7,81 |
–7,82 |
–7,81 |
–7,77 |
–7,77 |
–7,77 |
|
|
σ н xx |
–12,40 |
–12,40 |
–12,40 |
–12,30 |
–12,31 |
–12,31 |
|
|
н σθθ |
–56,53 |
–56,55 |
–56,56 |
–56,26 |
–56,27 |
–56,29 |
|
|
σ н xz |
–7,81 |
–7,81 |
–7,81 |
–7,76 |
–7,77 |
–7,77 |
|
|
т. Р : x = 0.0; ϕ= 0.0 |
w |
–0,5845 |
–0,5848 |
–0,5850 |
–0,5860 |
–0,5862 |
–0,5864 |
|
σ в xx |
62,12 |
62,14 |
62,16 |
61,74 |
61,77 |
61,79 |
|
|
в σθθ |
88,38 |
88,42 |
88,45 |
87,11 |
87,15 |
87,18 |
|
|
σ н xx |
–78,88 |
–78,91 |
–78,94 |
–78,98 |
–79,01 |
–79,04 |
|
|
σ н θθ |
–114,58 |
–114,63 |
–114,67 |
–115,00 |
–115,05 |
–115,09 |
|
|
т. С : x = 0.0; ϕ=π |
σ в xx |
62,11 |
62,14 |
62,16 |
61,74 |
61,77 |
61,79 |
|
в σθθ |
88,38 |
88,41 |
88,44 |
87,12 |
87,15 |
87,18 |
|
|
σ н xx |
–78,88 |
–78,92 |
–78,95 |
–78,98 |
–79,02 |
–79,04 |
|
|
н σθθ |
–114,59 |
–114,64 |
–114,68 |
–115,0 |
–115,05 |
–115,09 |
|
Таблица 3 / Table 3
Численные значения нормальных и сдвиговых напряжений на внутренней σ в и наружней σ н поверхностях эллиптического цилиндра при соотношении a/b =2/1
Numerical values of normal and shear stresses on the inner σ в in and outer σ н n surfaces of theelliptical cylinder with the ratio a/b =2/1
|
Координаты точек x , ϕ (м, рад) |
Напряжения, МПа, прогиб, см |
Вариант интерполяционной процедуры |
|||||||
|
Скалярная |
Векторная |
||||||||
|
Сетка узлов |
|||||||||
|
21 × 21 |
24 × 24 |
26 × 26 |
28 × 28 |
21 × 21 |
24 × 24 |
26 × 26 |
28 × 28 |
||
|
т. А : x = L / 2; ϕ= 0.0 |
σ в xx |
10,56 |
10,61 |
10,55 |
10,49 |
8,83 |
8,60 |
8,50 |
8,41 |
|
σ в θθ |
45,49 |
46,19 |
46,30 |
46,36 |
45,08 |
44,68 |
44,52 |
44,40 |
|
|
σ в xz |
–5,54 |
–6,35 |
–6,85 |
–7,34 |
–4,67 |
–5,19 |
–5,55 |
–5,92 |
|
|
σ н xx |
–10,36 |
–10,42 |
–10,37 |
–10,32 |
–8,63 |
–8,43 |
–8,34 |
–8,26 |
|
|
н σθθ |
–47,69 |
–48,62 |
–48,87 |
–49,07 |
–44,00 |
–43,85 |
–43,81 |
–43,79 |
|
|
σ н xz |
–5,54 |
–6,35 |
–6,85 |
–7,33 |
–4,67 |
–5,19 |
–5,55 |
–5,92 |
|
|
т. В : x = L /2; ϕ=π |
σ в xx |
5,29 |
5,26 |
5,21 |
5,17 |
8,83 |
8,60 |
8,50 |
8,41 |
|
σ в θθ |
26,09 |
26,44 |
26,52 |
26,56 |
45,08 |
44,68 |
44,52 |
44,40 |
|
|
σ в xz |
–2,81 |
–3,17 |
–3,40 |
–3,63 |
–4,67 |
–5,19 |
–5,55 |
–5,92 |
|
|
σ н xx |
–5,14 |
–5,11 |
–5,07 |
–5,03 |
–8,63 |
–8,43 |
–8,34 |
–8,26 |
|
|
н σθθ |
–27,84 |
28,38 |
–28,56 |
–28,70 |
–44,00 |
–43,85 |
–43,81 |
–43,79 |
|
|
σ н xz |
–2,81 |
–3,17 |
–3,40 |
–3,63 |
–4,67 |
–5,19 |
–5,55 |
–5,92 |
|
|
т. Р : x = 0.0; ϕ= 0.0 |
w |
–0,3333 |
–0,3433 |
–0,3464 |
–0,3487 |
–0,5551 |
–0,5579 |
–0,5592 |
–0,5602 |
Таблица 4 / Table 4
Численные значения нормальных и сдвиговых напряжений на внутренней σ в и наружней σ н поверхностях эллиптического цилиндра
Numerical values of normal and shear stresses on the inner σ в in and outer σ н n surfaces of the elliptical cylinder
|
Координаты точек x , ϕ (м, рад) |
Напряжения, МПа, прогиб, см |
Вариант интерполяционной процедуры |
|||||
|
Скалярная |
Векторная |
||||||
|
Число шагов нагружения |
|||||||
|
20 |
30 |
50 |
20 |
30 |
50 |
||
|
x = L /2; ϕ= 0.0 |
σ в xx |
10,48 |
10,48 |
10,48 |
8,49 |
8,48 |
8,47 |
|
σ в θθ |
45,77 |
45,78 |
45,79 |
44,19 |
44,19 |
44,19 |
|
|
σ в xz |
–6,50 |
–6,50 |
–6,50 |
–5,31 |
–5,30 |
–5,29 |
|
|
σ н xx |
–10,30 |
–10,30 |
–10,30 |
–8,32 |
–8,31 |
–8,30 |
|
|
н σθθ |
–48,26 |
–48,27 |
–48,28 |
–43,45 |
–43,45 |
–43,44 |
|
|
σ н xz |
–6,50 |
–6,50 |
–6,50 |
–5,30 |
–5,30 |
–5,29 |
|
|
x = L /2; ϕ=π |
σ в xx |
5,19 |
5,19 |
5,19 |
8,49 |
8,47 |
8,47 |
|
σ в θθ |
26,25 |
26,25 |
26,25 |
44,19 |
44,19 |
44,19 |
|
|
σ в xz |
–3,24 |
–3,24 |
–3,24 |
–5,31 |
–5,30 |
–5,29 |
|
|
σ н xx |
–5,05 |
–5,05 |
–5,05 |
–8,32 |
–8,31 |
–8,30 |
|
|
н σθθ |
–28,24 |
–28,24 |
–28,25 |
–43,45 |
–43,45 |
–43,44 |
|
|
σ н xz |
–3,24 |
–3,24 |
–3,24 |
–5,30 |
–5,30 |
–5,29 |
|
|
x = 0.0; ϕ= 0.0 |
w |
–0,3498 |
–0,3499 |
–0,3501 |
–0,5671 |
–0,5674 |
–0,5677 |
|
σ в xx |
76,85 |
76,91 |
76,95 |
95,42 |
95,52 |
95,61 |
|
|
σ в θθ |
93,65 |
93,71 |
93,75 |
106,98 |
107,08 |
107,15 |
|
|
σ н xx |
–91,82 |
–91,89 |
–91,95 |
–106,86 |
–106,98 |
–107,08 |
|
|
σ н θθ |
–120,51 |
–120,60 |
–120,67 |
–130,53 |
–130,67 |
–130,78 |
|
|
x = 0.0; ϕ=π |
σ в xx |
62,46 |
62,49 |
62,51 |
95,42 |
95,53 |
95,61 |
|
в σθθ |
67,40 |
67,43 |
67,46 |
106,98 |
107,08 |
107,16 |
|
|
σ н xx |
–76,00 |
–76,05 |
–76,08 |
–106,86 |
–106,98 |
–107,08 |
|
|
н σθθ |
–91,53 |
–91,58 |
–91,62 |
–130,53 |
–130,67 |
–130,78 |
|
Исходя из анализа табличного материала, можно сделать вывод, что при определении НДС эллиптического цилиндра в геометрически нелинейной постановке стандартная интерполяционная процедура не приводит к достижению корректного результата. При расчёте эллиптического цилиндра следует применять разработанную векторную форму интерполяции компонент вектора шагового перемещения и шагового вектора углов поворота нормали.
Следует отметить, что указанная некорректность стандартной интерполяционной процедуры будет возрастать с увеличением кривизны поперечного сечения эллиптического цилиндра. Выполним расчёт эллиптического цилиндра с вышеприведенными исходными данными при соотношении параметров эллипса поперечного сечения, равного a / b = 3/1, а также a / b = 4/1.
Для наглядности результаты расчетов представим в графической форме. Введём коэффициенты, показывающие отношения нормальных и сдвиговых напряжений в точках A и B при количестве шагов нагружения, равном
-
50, и сетке дискретизации 25 × 25: β= ( σ в ) / ( σ в ) ;
-
1 xx Axx B β 2 = ( σ ϕ н ϕ ) A / ( σ н ϕϕ ) B ; β 3 = ( σ в xz ) A / ( σ в xz ) B ..
На рис. 2–7 показаны изменения вышеупомянутых коэффициентов β 1, β 2 и β 3 в зависимости от соотношения параметров эллипса поперечного сечения эллиптического цилиндра а / b в первом и во втором вариантах расчёта соответственно. Как видно из рисунков, с увеличением отношения а / b значения коэффициентов β 1, β 2, β 3 в первом варианте существенно возрастают, что является совершенно неприемлемым. Во втором варианте наблюдаем стабильное значение коэффициентов β 1, β 2 и β 3 , равное единице, что и следует ожидать, исходя из условия симметрии расчётной схемы эллиптического цилиндра.
Для более полной картины НДС эллиптического цилиндра (при соотношении параметров эллипса поперечного сечения a / b = 2/1) на рис. 8 и 9 представлены графики изменения нормальных напряжений σ 11 и σ 22
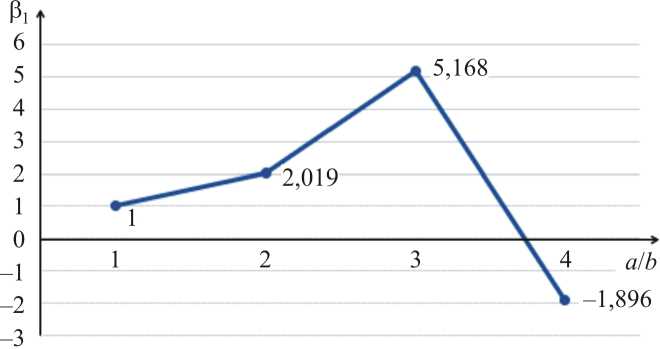
Рис. 2. Изменение значений коэффициентов в =
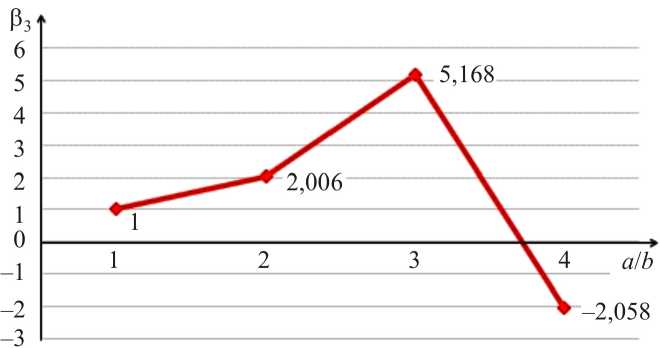
Рис. 4. Изменение значений коэффициентов В, = . xz A
3 (° ) В в зависимости от отношения полуосей эллипса а / b поперечного сечения эллиптического цилиндра при стандартной интерполяции искомых величин
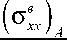
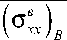
в зависимости от отношения полуосей эллипса а / b поперечного сечения эллиптического цилиндра при стандартной интерполяции искомых величин
Fig. 2. Change in the values of the coefficients P 1 =
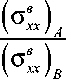
Fig. 4. Change in the values of the coefficients P 3 =
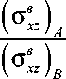
depending on the ratio of the semiaxes of the ellipse а / b of the cross section of the elliptical cylinder with standard interpolation of the sought values depending on the ratio of the semiaxes of the ellipse а / b of the cross section of the elliptical cylinder with standard interpolation of the sought quantities
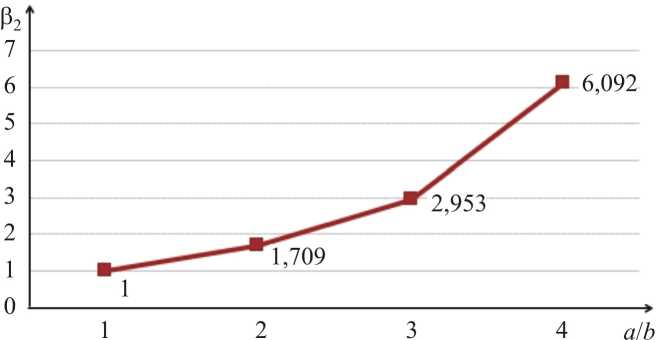
Рис. 3. Изменение значений коэффициентов в2 = ч--- —-
(° ее ) в
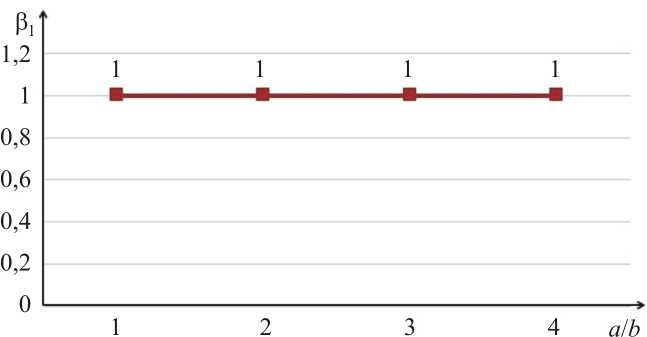
Рис. 5. Изменение значений коэффициентов
P t
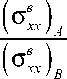
в зависимости от отношения полуосей эллипса а / b поперечного сечения эллиптического цилиндра при стандартной интерполяции искомых величин в зависимости от отношения полуосей эллипса а / b поперечного сечения эллиптического цилиндра при векторной интерполяции искомых величин
Fig. 3. Change in the values of the coefficients в =
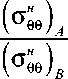
Fig. 5. Change in the values of the coefficients
P t
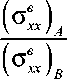
depending on the ratio of the semi-axes of the ellipse а / b of the cross section of the elliptical cylinder with standard interpolation of the sought quantities depending on the ratio of the semi-axes of the ellipse а / b of the cross-section of the elliptical cylinder with vector interpolation of the sought quantities вдоль образующих цилиндра (при ф = 0 и ф = п) при сетке узлов 25x25 и количестве шагов нагружения, равном 30. Анализ графического материала показывает, что в первом варианте расчета, т.е. при скалярной интерполяции искомых величин на шаге нагружения, существенные различия между значениями напряжений сохраняются на протяжении всей длины образующих при ф = 0 и ф = п. И, напротив, во втором варианте расчета полное совпадение параметров НДС наблюдается вдоль всей длины образующих эллиптического цилиндра при ф = 0 и ф = п, что является необходимым критерием корректности разработанного алгоритма при выбранной расчетной схеме.
На рис. 10 и 11 представлены графики изменения нормальных напряжений o 22 в зависимости от угловой координаты ф ( 0 <ф<п ) в концевом и срединном сечениях эллиптического цилиндра при различных вариантах интерполяционной процедуры искомых величин на шаге нагружения. Анализ графического материала, представленного на рис. 10, 11, показывает, что распределение напряжений существенно различается по вариантам расчета, особенно в срединной области дуги
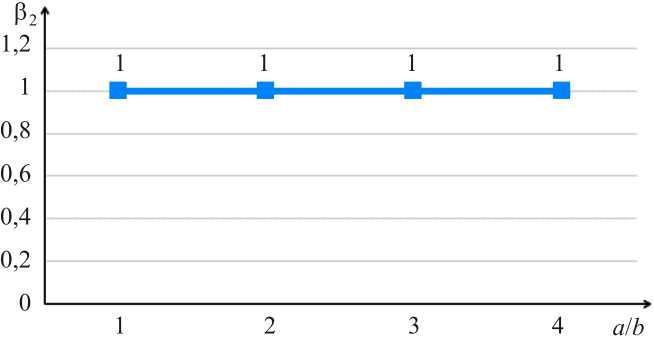
Рис. 6. Изменение значений коэффициентов в = —-
( ° : . ) в
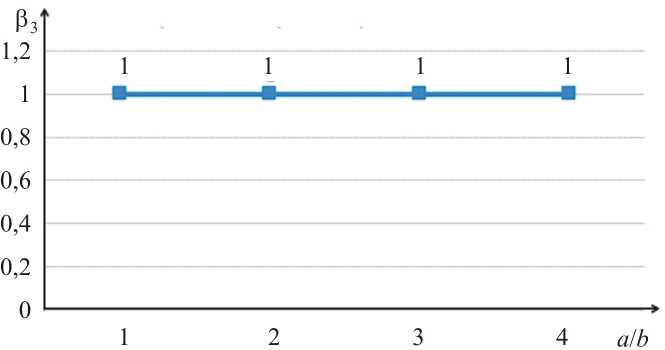
Рис. 7. Изменение значений коэффициентов
0 3 =
в зависимости от отношения полуосей эллипса а / b поперечного сечения эллиптического цилиндра при векторной интерполяции искомых величин в зависимости от отношения полуосей эллипса а / b поперечного сечения эллиптического цилиндра при векторной интерполяции искомых величин
Fig. 6. Change in the values of the coefficients P 2 = -.--- —-
( ° .. ) В
Fig. 7. Change in the values of the coefficients
0 3 =
depending on the ratio of the semi-axes of the ellipse а / b of the cross section of the elliptical cylinder with vector interpolation of the sought quantities depending on the ratio of the semi-axes of the ellipse а / b of the cross-section of the elliptical cylinder with vector interpolation of the sought quantities
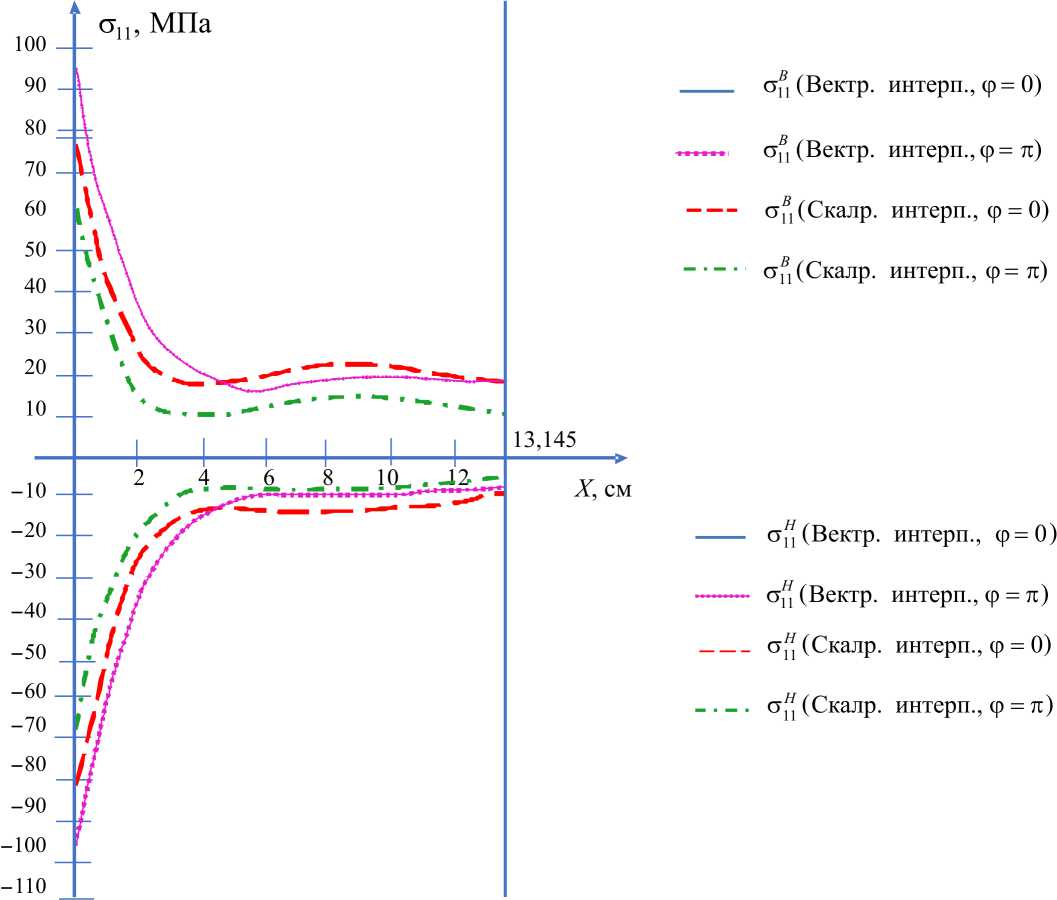
Рис. 8. Графики изменения нормальных напряжений 0 ^ 1 ,° 1 1 вдоль образующих цилиндра ( ф = 0 и ф = П )
при различных вариантах интерполяции искомых величин
Fig. 8. Graphs of changes in normal stresses о® , о11 along the generatrix of the cylinder ( ф = 0 и ф = П ) with different options for interpolation of the sought values
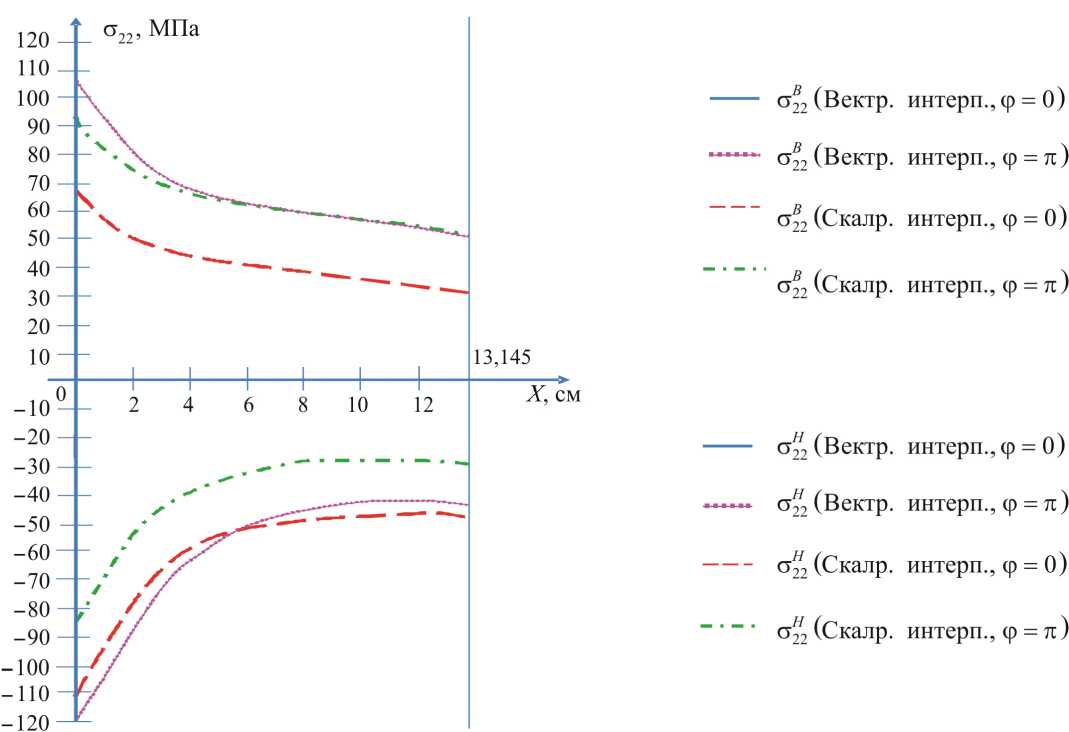
Рис. 9. Графики изменения нормальных напряжений σ 2 B 2 , σ 2 H 2 вдоль образующих цилиндра ( ϕ= 0 и ϕ =π )
при различных вариантах интерполяции искомых величин
Fig. 9. Graphs of changes in normal stresses σ 2 B 2 , σ 2 H 2 along the generatrix of the cylinder ( ϕ= 0 и ϕ =π ) with different options for interpolation of the sought values
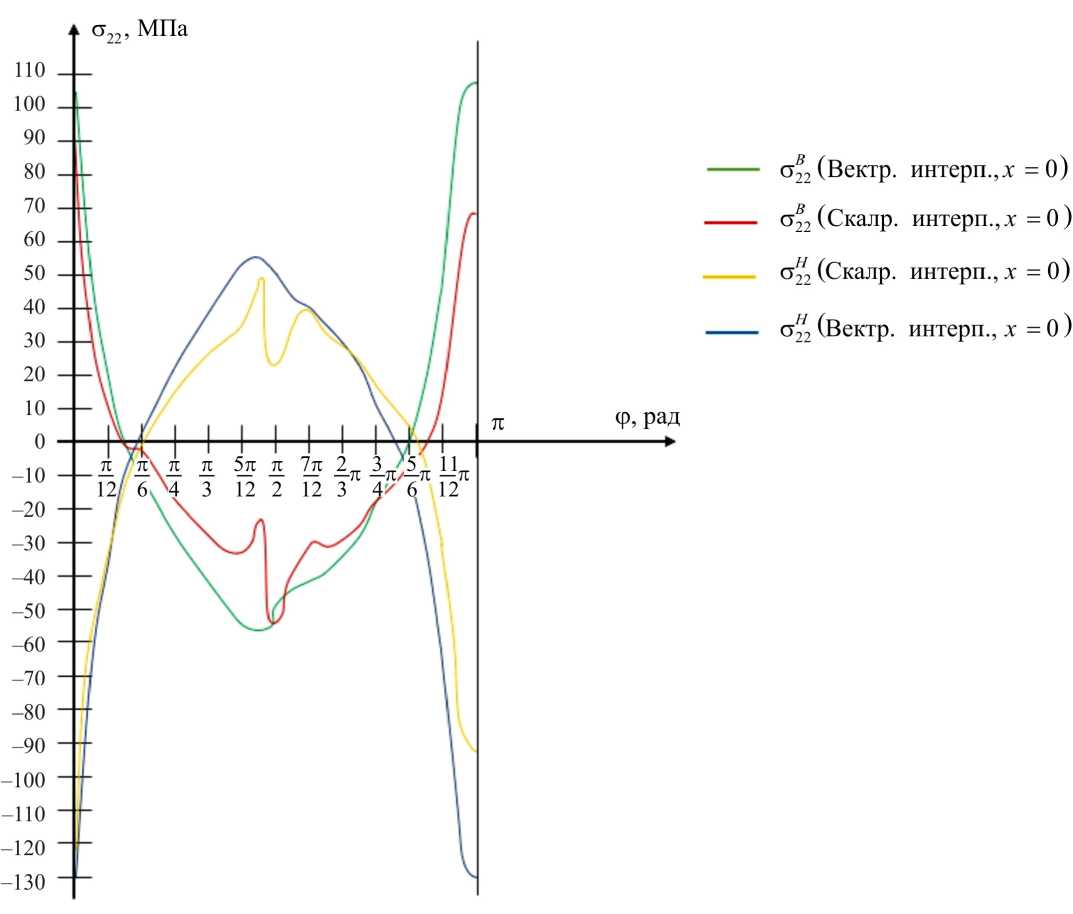
Рис. 10. Эпюры нормальных напряжений σ 22 в срединном сечении эллиптического цилиндра при различных вариантах интерполяции искомых величин
Fig. 10. Diagrams of normal stresses σ 22 in the middle section of an elliptical cylinderwith different options for interpolation of the sought values
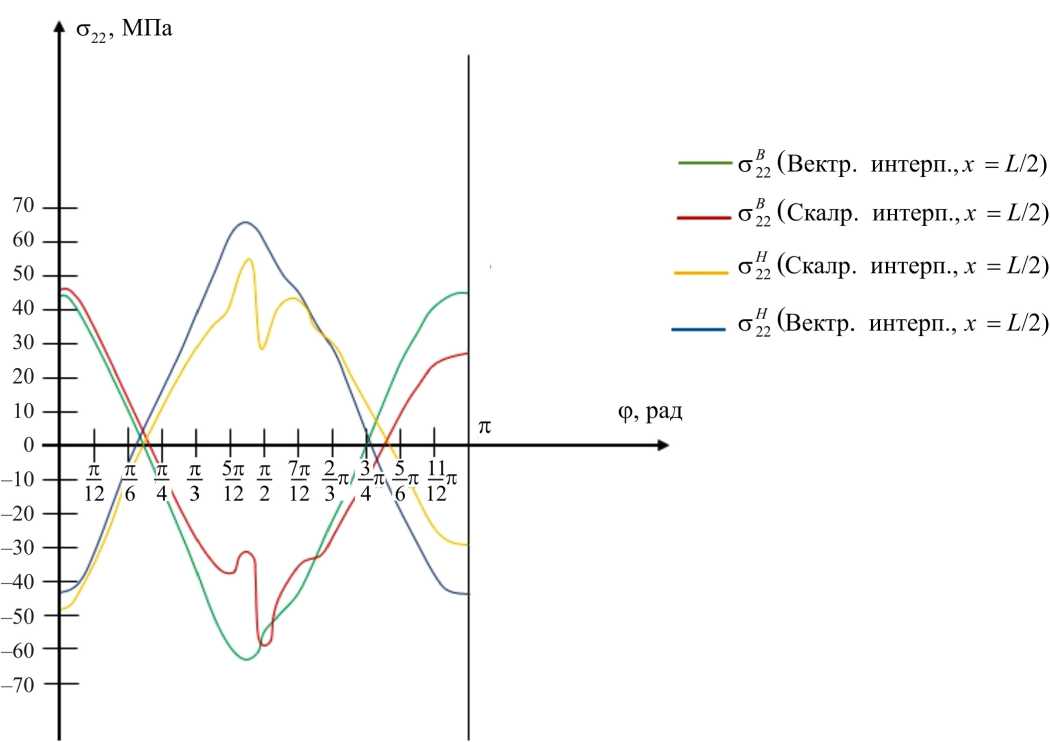
Рис. 11. Эпюры нормальных напряжений σ 22 в концевом сечении эллиптического цилиндра при различных вариантах интерполяции искомых величин
Fig. 11. Diagrams of normal stresses σ22 in the end section of an elliptical cylinderwith different options for interpolation of the sought values поперечного сечения и в зоне от 5π/6 до π . Так, в первом варианте расчета (при использовании стандартной скалярной интерполяции шаговых искомых величин) в интервале от 5π/12 до 7π/12 наблюдаются скачки в эпюрах напряжений, что явно свидетельствует о некорректности скалярной интерполяционной процедуры, так как в данной зоне отсутствуют локально приложенные нагрузки. Кроме того, на графиках отчетливо прослеживается существенное различие в значениях напряжений в точках ϕ = 0 и ϕ =π. И, напротив, во втором варианте расчета (в котором реализована разработанная векторная форма интерполяции шаговых искомых неизвестных) наблюдается полное совпадение напряжений в точках с угловыми координатами ϕ= 0и ϕ =π, что ожидаемо следует из симметрии выбранной расчетной схемы. Анализируя графики напряжений второго варианта расчета, также можно констатировать отсутствие скачков в эпюрах напряжений и симметрию численных значений напряжений, вычисленных на внутренней и наружной поверхностях эллиптического цилиндра относительно нейтральной оси.
Список литературы Конечно-элементный расчет эллиптического цилиндра в геометрически нелинейной постановке при использовании векторной формы интерполяционной процедуры
- Storozhuk E.A., Yatsura A.V. Analytical-numerical solution of static problems for noncircular cylindrical shells of variable thickness // International Applied Mechanics. - 2017. - Vol. 53, № 3. - P. 313-325.
- Yatsura A.V., Storozhuk E.A. Exact solutions of boundary-value problems for noncircular cylindrical shells // International Applied Mechanics. - 2016. - Vol. 52, № 4. - Р. 386-397.
- Хайруллин Ф.С., Мингалиев Д.Д. Расчет тонких оболочек с использованием аппроксимирующих функций различного порядка // Вестник Казанского технологического университета. - 2017. - Т. 20, № 14. - С. 102-104.
- Transformable calculation schemes in geometrically nonlinear problems of mechanics of sandwich plates with the contour reinforcing beams / V.N. Paimushin [et al.] // Journal of Physics: Conference Series. - 2019. - P. 032043.
- Badriev I.B., Paimushin V.N. Refined models of contact interaction of a thin plate with positioned on both sides deformable foundations // Lobachevskii Journal of Mathematics. - 2017. -Vol. 38, № 5. - P. 779-793.
- Yants A.Y., Trusov P.V. Geometrically nonlinear constitutive equations of the plastic flow theory in terms of asymmetric stress and strain measures // IOP Conference Series: Materials Science and Engineering. - 2019. - Р. 012034.
- Численное моделирование работы настила с учетом несовершенств крепления в физически и геометрически нелинейной постановке / Р.А. Каюмов [и др.] // Инновационные машиностроительные технологии, оборудование и материалы - 2019 (МНТК «ИМТОМ - 2019»): сборник материалов Х Международной научно-технической конференции. - Казань, 2019. - С. 51-54.
- Rogovoy A.A., Salikhova N.K. Finite-element modeling of plastic working of steel billets // Solid State Phenomena. - 2016. -Vol. 243. - Р. 75-81.
- Каюмов Р.А., Шакирзянов Ф.Р., Гаврюшин С.С. Моделирование процесса деформирования и оценка несущей способности системы грунт - тонкостенная конструкция // Известия высших учебных заведений. Машиностроение. - 2014. -№ 6. - С. 20-24.
- Роговой А.А., Салихова Н.К. Конечно-элементное моделирование формоизменения и напряженно-деформированного состояния стального слитка в процессе прессования // XIX Зимняя школа по механике сплошных сред: сборник статей / отв. ред. Н.А. Юрлова. - 2015. - С. 256-261.
- TyukalovYu.Ya. Finite element models in stresses for bending plates // Инженерно-строительныйжурнал. - 2018. -№ 6 (82). -С. 170-190.
- Lalin V., Rybakov V., Sergey A. The finite elements for design of frame of thinwalled beams // Applied Mechanics and Materials. - 2014. - Vol. 578-579. - Р. 858-863.
- Yakupov N.M., Kiyamov H.G., Mukhamedova I.Z. Simulation of toroidal shell with local defect // Lobachevskii Journal of Mathematics. - 2020. - Vol. 41, № 7. - Р. 1310-1314.
- Игнатьев А.В., Игнатьев В.А., Гамзатова Е.А. Расчет тонких пластин по методу конечных элементов в форме классического смешанного метода с исключением перемещений конечных элементов как жесткого целого // Известия высших учебных заведений. Строительство. - 2018. - № 3 (711). - С. 5-13.
- FEM Vector Approximation for a Shell of Revolution with Account for Shear Deformations / Yu.V. Klochkov [et al.] // Journal of Machinery Manufacture and Reliability. - 2020. -Vol. 49, № 4. - P. 301-307.
- The finite element approximation of vector fields in curvilinear coordinates / A.Sh. Dzhabrailov [et al.] // Russian Aeronautics. - 2007. - Vol. 50, № 2. - Р. 115-120.
- Седов Л.И. Механика сплошной среды. - М.: Наука, 1976. - 574 с.
- Серазутдинов М.Н., Убайдуллоев М.Н. Метод расчета упругопластического деформирования усиленных стержневых конструкций при различных режимах нагружения // Известия Казанского государственного архитектурно-строительного университета. - 2018. - № 4 (46). - С. 370-377.
- Голованов А.И., Тюленева О.Н., Шигабутдинов А.Ф. Метод конечных элементов в статике и динамике тонкостенных конструкций. - М.: Физматлит, 2006. - 392 с.
- Бате, К., Вилсон Е. Численные методы анализа и метод конечных элементов. - М.: Книга по требованию, 2012. - 445 с.
- Косицын С.Б., Чан С.Л. Анализ напряженно-деформированного состояния пересекающихся цилиндрических оболочек при упругопластических деформациях с учетом геометрической // Строительная механика инженерных конструкций и сооружений. - 2013. - № 1. - С 3-9.
- Sheshenin S.V., Bakhmet'ev S.G. A model of the effec-tiverubber-cord ply // Moscow university mechanics bulletin. -2014. - Vol. 69, № 5. - P. 109-113.
- Contemporary problems of numerical modelling of unique structures and buildings / A.M. Belostotsky [et al.] // International Journal for Computational Civil and Structural Engineering. -2017. - Vol. 13, № 2. - С. 9-34.
- Galishnikova V.V. Pahl P.Ja. Analysis of frame buckling without sidesway classification // Structural mechanics of engineering structures and structures. - 2018. - Vol. 14, № 4. - Р. 299-312.
- Nguyen Nhung, WaasAnthonym. Nonlinear, finite deformation, finite element analysis // ZAMP. Z. Angew. math.and Phys. - 2016. - Vol. 67, № 9. - P. 35/1-35/24.
- Paznanova S.L., Vasilev G.P., Dineva P.S. Dynamic analysis of nanoheterogeneities in a finite-sized solidby boundary and finite element methods // Int. J. Solids and Struct. - 2016. - Vol. 80. - P. 1-18.
- Lei Zhen, Gillot Frederic, Jezeguel. Developments of the mixed grid isogeometricReissner-Mindlin shell: serendipity basis and modified reduced quadrature // Int. J. Mech. - 2015. - Vol. 54. - P. 105-119.
- Wriggers P., Reddy B., Rust W. Efficient virtual element formulations for compressible and incompressible finite deformations // Computational Mechanics. - 2017. - Vol. 60. - P. 253-268.
- Artioli E., Veiga L.B.D., Lovadina C. Arbitrary order 2d virtual elements for polygonal meshes: Part ii, inelastic problem // Computational Mechanics. - 2017. - Vol. 60. - P. 643-657.
- Krysl P. Mean-strain 8-node hexahedron with optimized energy-sampling stabilization // Finite Elements in Analysis and Design. - 2016. - Vol. 108. - P. 41-53.
- Magisano D, Leonetti L, Garcea G. Koiter asymptotic analysis of multilayered composite structures using mixed solidshell finite elements // Composite Structures. - 2016. - Vol. 154. -Р. 296-308. DOI: 10.1016/j.compstruct.2016.07.046.
- Liang K, Ruess M, Abdalla M. Co-rotational finite element formulation used in the Koiter-Newton method for nonlinear buckling analyses // Finite Elements in Analysis and Design. -2016. - Vol. 116. - P. 38-54.
- Chi H., Talischi C., Lopez-Pamies O. Polygonal finite elements for finite elasticity // International Journal for Numerical Methods in Engineering. - 2015. - Vol. 101. - P. 305-328.
- BishopJ.A displacement-based finite element formulation for general polyhedra using harmonic shape functions // Internat. J. Numer. Methods Engrg. - 2014. - Vol. 97 (1). - P. 1-31.
- Talischi C., Pereira A., Menezes I.F.M. Gradient correction for polygonal and polyhedral finite elements // Internat. J. Numer. Methods Engrg. - 2015. - Vol. 102 (3-4). - P. 728-747.


