Конечно-элементный расчет трехслойной балки

Автор: Нестеров Владимир Анатольевич

Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau

Рубрика: Математика, механика, информатика

Статья в выпуске: 2 (35), 2011 года.

Бесплатный доступ

Рассматривается новый конечный элемент балки, в расчетах которой учитывается трансверсальный сдвиг. При этом в каждом из узлов конечного элемента в качестве основных кинематических параметров присутствуют осредненные по толщине углы трансверсального сдвига. Представлены результаты численного исследования, демонстрирующие отсутствие эффекта сдвигового запирания в новой балочной конечноэлементной модели.

Балка, трансверсальный сдвиг, метод конечных элементов, эффект сдвигового запирания

Короткий адрес: https://sciup.org/148176568

IDR: 148176568

Текст научной статьи Конечно-элементный расчет трехслойной балки

В последнее время в авиационной и ракетнокосмической отрасли все чаще применяются новые конструкционные материалы, позволяющие изготавливать технику разнообразного назначения с высокими удельными характеристиками. Среди прочих осо- бое место занимают композиционные материалы. Обладая высокой удельной прочностью и жесткостью, композиты, кроме того, позволяют проектировать конструкции с требуемыми механическими свойствами в зависимости от их назначения и условий экс- плуатации. Однако композитные конструкции, в том числе и балки, отличаются рядом особенностей, которые необходимо учитывать при проектировании и расчете. И основная среди них – низкая сдвиговая жесткость по отношению к трансверсальным напряжениям. Учет указанной особенности приводит к повышению порядка разрешающих уравнений за счет введения в рассмотрение углов трансверсального сдвига.

В данной работе представлен новый конечный элемент балки, в расчете которой учитывается трансверсальный сдвиг. При этом рассматривается модель, базирующаяся на математической теории пластин Рейсснера–Миндлина. При выводе основополагающих соотношений теории метода конечных элементов используется вариационный подход, при котором в качестве исходного фигурирует выражение потенциальной энергии деформации конструкции. Для сдвиговой модели балки это выражение имеет вид

E = 1 [ ^f Ndu + Md ⁶ + Q _v) dx - \qwdx . (1)

2 0 V dx dx J 00

В выражении (1) фигурируют следующие кинематические параметры: θ – угол наклона сечения, измеряемый в плоскости XZ (рис. 1); u – перемещения точек начальной плоскости вдоль продольной оси балки; w – прогибы точек начальной плоскости; ψ – угол сдвига, или осредненная по высоте сечения деформация трансверсального сдвига, вычисляемая по формуле [1]

1 h - s

V = 7 J e xz dz , h

-s где h – высота сечения балки (толщина балки); (h–s) и (–s) – координаты по высоте верхней и нижней поверхности балки соответственно.

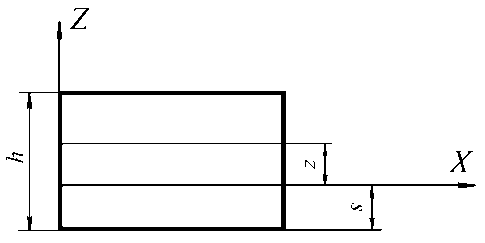
Рис. 1. Система координат в слоистой структуре

Полный угол наклона сечения представляет собой сумму двух слагаемых:

6 = v

dw dx

где dw/dx – угол наклона сечения, происходящий за счет изгиба балки.

В энергетическом функционале (1) присутствуют силовые факторы: q – погонная балочная нагрузка и N , M , Q – внутренние балочные усилия ( N – продольная сила; М – изгибающий момент; Q – перерезывающая сила), которые связаны с кинематическими параметрами посредством следующих физических соотношений:

N = Bdu + Cd6, M = Cdu + D —, Q = Kv , (3) dx dx dx dx где B, C, D и K – жесткостные параметры балки: В определяет жесткость балки при растяжении-сжатии вдоль продольной оси; С – так называемая смешанная жесткость; D – изгибная жесткость; К – жесткость балки при трансверсальном сдвиге.

Получим матрицу жесткости конечного элемента и вектор эквивалентной узловой нагрузки для балки, нагруженной погонной нагрузкой q , для случая низкой трансверсальной сдвиговой жесткости. Будем полагать нагрузку постоянной вдоль одного конечного элемента. В качестве основных узловых неизвестных будем рассматривать прогиб w , изгибной угол наклона сечения, угол трансверсального сдвига и продольное перемещение u (рис. 2).

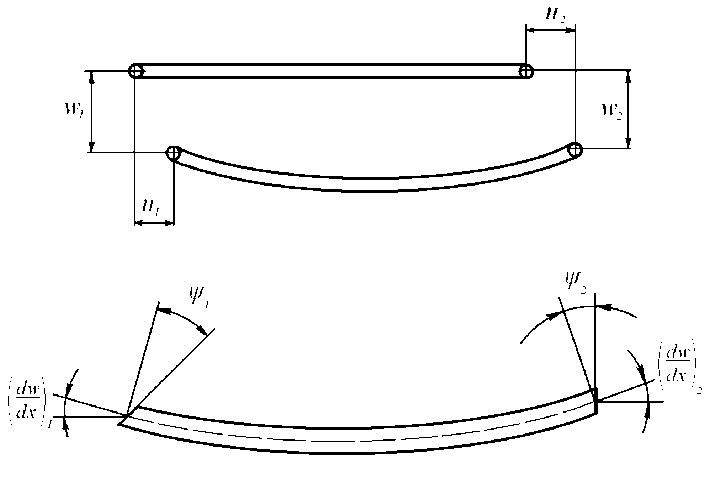
Рис. 2. Узловые параметры балочного конечного элемента

Будем полагать, что прогиб изменяется по кубическому закону вдоль длины элемента, а угол сдвига ψ и продольное перемещение u – по линейному закону:

w(x) = a1 + a2x + a3x2 + a4x3 , v(x) = a5 +a6x , u(x) = a7 +a8x.

Основные кинематические параметры в произвольной точке конечного элемента можно выразить через их узловые значения:

δ = P δ e , (5)

где f dw о = ^ w — v u

I dx

„ f f dw) f dw A

°e = 1 w1 hr I V1 u1 w2 1-^1V

I V ^dx J 1 V ^dx J 2

u 2 1 . (7)

Матрица P имеет следующую структуру:

p11 p12 00p15 p16

p21 p22 00p25 p26

00p33 000p370

000 p ₄₄ 000 p ₄₈

и компоненты

x ² x ³

^Р 11 = ^{1 3} l 2 ⁺ ² l³ ’

23 x ² x ³

^P 15 = ³ l 2 ² l³ ’

p 12

= x - 2 + l2

x ²

x ³

l + l2

xxxx

P 21 = - P 25 = 6 + 677 , P 22 = 1 - 4V + 377, l2l3

x x2

P 26 =^- ² J + ³ P 33 = P 44 = ¹ — J ^

^P 37 = ^P 48 = J •

Здесь l – длина балочного элемента.

Запишем матричное выражение (5) в виде следующих соотношений:

f, ²

x ³

I J .x 2, x ³ J

f dw I

w =

I ^{1 3} l²

⁺² F

w + x - 2-- +

^J ¹ I l l ² J

l 7- I ⁺I dx J ,

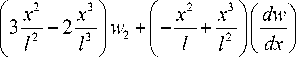
dw = ^f dx |

- 6 x

A x ² J , ⁶ T^r J w ⁺

^f 1 - 4 x + 3

1 1

x ²

l ²

if dw J

■

Ji dx J j

(8)

⁺ |

⁶ x -

x ²1 f у² 1 ^w 2 ⁺I

- 2 x + 3 x^

ll ²

dw J

dx J₂ ’

V = f 1

x I -

l J

V 1

⁺ L v ²,

u = l 1 -

x I

L j

J ^u1 ⁺ yu 2 .

С учетом соотношения углов (2) перепишем физические соотношения (3) в виде

du 1 d V d ² w I

N = B + C l - I , dx | dx dx 1

du f d V

M = C + D l dx I dxdx

С помощью (8) вычислим фигурирующие производные:

du u ₂ - u 1

d V _ V 2 — V 1

d 2 w

dx ²

6 12 x J f 4 6 x Jf dw J

—— + w + - + + l2 l3 J 1 I l l2 JI dx J1

6 6 x । f 2 6 x If dw I L ^- "J 7 ^J ^w ² ⁺ | ^- J ⁺" J 7 Д dx ^J 2

Подставим физические соотношения в перемещениях (9) в выражение полной потенциальной энергии (1), а затем заменим все фигурирующие в нем кинематические переменные (и соответствующие производные) их выражениями через узловые неизвестные (8), (10). Выполним интегрирование по длине конечного элемента балки. Полученную функцию полной потенциальной энергии продифференцируем по каждой из компонент вектора δ_e . В результате получим систему уравнений равновесия произвольного балоч-

ного элемента, которая в матричном представлении имеет следующий вид:

K_e δ_e = F_e ,

где K e – матрица жесткости балочного элемента;

F e – вектор эквивалентных узловых сил.

Матрица жесткости симметрична относительно главной диагонали:

		" k u k 12	00	k 15	k 16 0	0 "
		k 22	k 23 k 24	k 25	k 26 k 27	k 28
			k 33 k 34	0	k 36 k 37	k 38
	K e =		k 44	0	k 46 k 47	k 48	, (12)
				k 55	k 56 0	0
					k 66 k 67	k 68
		c	им	м	k 77	78
		.				k 88 _
		D	D		D		D
где	k11 =	12 _l ^D ₃ ;	^k 12 = ⁶ J 7	k ₁₅	⁼ - ¹² 7	^k 16 = ⁶ J 2 ;
	, D		D		C		D
k 22	= 4— l	; k ₂₃	=-- l ^;	k 24	= l^;	k 25	l ²;

k 26	= 2 D l	; k	27 ⁼	D l ^;	28	C = l^;	33 ⁼	D — + l	Kl 3^;	^C k 34 = l
k 36	D = l ^;	37	= -	D — + l	Kl 6^;	Jr.. = 38 ⁼	C l^;	k 44	B = l ^;	k⁴⁶ =
k 47	C =-- l	;	k 48	=-	B ™ ^^^^^^^^^^^ l ^;	k 55	= 12	D l 3 ;	k 56	=- 6 D
k 66	= 4 D l	;	k 67	=-	D l ^;	k 68	C = l	;	Jr__= 77 ⁼	DKl + l 3
78	C = l ^;	k 88	B = _l	.

Вектор эквивалентных узловых сил имеет следующий вид:

Т f = J qL qL 00 ql -q_ 0 ol . (13)

I 2 12 2 12 I

Рассмотрим балку длиной L , разбитую на n конечных элементов (рис. 3). Выделим i -й конечный элемент.

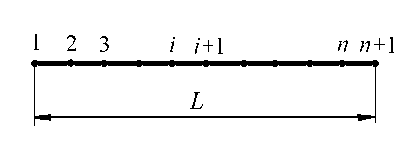
Рис. 3. Конечно-элементная модель балки

Полученная для него по описанной выше процедуре система уравнений равновесия имеет вид

K_e ( i ) δ_e ( i ) = F_e ( i ) ,

где δ e ⁽ ⁱ ⁾ – вектор узловых неизвестных i -го элемента, соединяющего i -й и i + 1-й узлы, K_e ⁽ ⁱ ⁾ и F_e ⁽ ⁱ ⁾ – матрица

жесткости и вектор эквивалентной узловой нагрузки i -го конечного элемента, определяемые как (12) и (13) соответственно.

Сформируем глобальный вектор узловых неизвестных. Для этого введем в рассмотрение вектор узловых неизвестных i -го узла одномерной КЭ сетки:

δ i =

dw )

V, U dx ) i

Тогда глобальный вектор узловых неизвестных можно представить в виде

Δ = { δ 1 δ 2 … δ i … δ n +1 } ^Т . (16)

Чтобы получить глобальную матрицу жесткости и глобальный вектор узловых нагрузок, необходимо записать выражение полной потенциальной энергии для всего ансамбля конечных элементов:

E z=K U . + П ) .

i = 1

	' 12 D	6 D	0	⁰
	- l з	l ²
K II =	6 D	2 D	D	C
	- l 2	l	l	l
	⁰	D	Kl ² - 6 D	C
		l	6 l	l
		C	C	^B
	L ⁰	l	l	- l
	■ 12 D	6 D	0
	l ³	l ²		⁰
K III =	6 D	2 D	D	C
	l ²	l	l	l
	⁰	D	Kl ² - 6 D	C
		l	6 l	l
		C	C	B
	0	—	_-
	L	l	l	l
	12 D	6 D	0
	l ³	^- l 2
K iv =	6 D	4 D	D	C
	- l ²	l	l	^- 1
	0	D	2 Kl ² + 6 D	C
		l	6 l	l
	⁰	C	C	В
		l	l	l J

Выражения потенциальной энергии деформации и потенциала внешних сил отдельных элементов получаются по описанной выше процедуре. В результате преобразований получим выражение полной потенциальной энергии балки как функцию от всех узловых неизвестных:

Ez = f I w

dw dx

V U

i = 1, 2, к n + 1.

Дифференцируя (18) по каждой компоненте глобального вектора неизвестных (16), получим следующую СЛАУ, являющуюся системой уравнений равновесия всей балки:

Тогда глобальную матрицу жесткости однородной балки постоянной жесткости, состоящую из конечных

элементов равной дующим образом:		длины,	можно	сформировать сле-
Ki	Kn	0	0	0	0
Кщ	Ki + Krv	Kn	0	0	0
K-= 0	Кщ	Ki + K_rv	K_n	0	0	(21)
0	0	Кщ	Ki + Kp,	Kn	0	(21)
0	0	0	Кщ	Ki + K_IV	Kn
0	0	0	0	Кщ	Kiv

K Σ Δ = F Σ , (19)

где K Σ – глобальная матрица жесткости балки; F Σ – глобальный вектор эквивалентных узловых сил.

Глобальную матрицу жесткости и глобальный вектор нагрузки можно сформировать по более простой процедуре [2]. Для этого матрицу жесткости элемента представим в блочном виде:

Здесь под 0 следует понимать нулевые матрицы размером 4 × 4.

Для удобства интерпретации представлена глобальная матрица жесткости для балки, состоящей из 5 конечных элементов. Глобальный вектор нагрузки в этом случае будет иметь следующий вид:

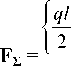
^ql ² 00 ql 000

00 ql 000 ^ql

ql 000 ql

ql ²

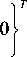
K I K II

K III K IV

где K_I , K_II , K_III , K_IV – подматрицы размером 4 × 4 – имеют следующее представление:

	2 D l ³	6 D l ²	0	0
K i =	6 D	4 D	D	C
K i =	l ²	l	l	l
	0	D	2 Kl ² + 6 D	C
	0	l	6 l	l
	0	C	C	B
	0	l	l	l

Следует иметь в виду, что в разрешающей СЛАУ (19) необходимо учесть граничные условия.

Одной из самых распространенных конструкций, в расчетах которых необходимо учитывать трансверсальный сдвиг, является трехслойная оболочка с податливым заполнителем. Рассмотрим модель трехслойной балки (рис. 4). Будем полагать, что жесткость несущих слоев существенно выше жесткости промежуточного слоя. В этом случае можно допустить, что параметры жесткости балки B , C и D обеспечены несущими слоями.

При совпадении начальной плоскости со срединной плоскостью балки и при симметричной структуре слоистого пакета смешанные жесткости ( C ) равны нулю. Остальные параметры жесткости вычисляются по формулам

2 E н bt D = E н b ( H ³ - h ³)

1 -ц Н , 12(1 -ц Н )

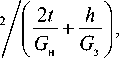
где H - полная толщина пакета; h - толщина слоя заполнителя; t - толщина каждого из несущих слоев; b - ширина сечения; Е _н - приведенный модуль упругости материала несущих слоев; G _н и G _з - модули сдвига материалов несущих слоев и заполнителя соответственно.

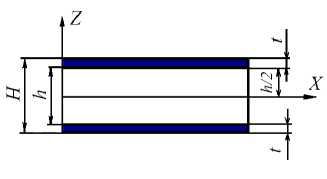
Рис. 4. Трехслойная конструкция

Как известно, в последнее время получила распространение конечно-элементная модель податливых при трансверсальном сдвиге балок, в которой в качестве основных узловых переменных фигурируют продольные перемещения и прогибы точек продольной оси и полный угол поворота сечения (6). Эта модель с тремя кинематическими параметрами в узле обладает определенным недостатком, который называется эффектом сдвигового запирания (ЭСЗ).

Для того чтобы выяснить, не проявится ли эта же проблема в решениях с использованием нашей КЭ-модели, проведем следующий численный эксперимент. Выполним две серии расчетов для балок различной толщины. В первой серии будет задействована рассматриваемая в данной работе модель с 4 узловыми кинематическими параметрами. Во второй се- рии нужно использовать конечно-элементную модель, основывающуюся на классической теории оболочек Кирхгофа. В этой классической модели в каждом узле присутствует 3 кинематических переменных: продольное перемещение, прогиб и изгибной угол поворота нормали (dw/dx). Таким образом, вектор узловых неизвестных балочного элемента в данном случае имеет следующий вид:

Статья научная