Конечноэлементная математическая модель динамики криволинейного трубопровода с пульсирующим потоком рабочей жидкости

Исследование динамических характеристик, процессов генерации и распространения колебаний в гидрогазовых систем с каждым годом привлекает внимание все большего числа ученых. Зарубежными и отечественными исследователями накоплен определенный опыт в данной научной области, разработаны математические модели динамических процессов в элементах и узлах систем. Однако все они обладают определенной долей идеализации, различными допущениями и ограничениями.

Ранее были разработаны математические модели процессов связанных колебаний жидкой среды и твердотельных элементов в элементарном объеме на границе раздела сред [3]. Однако данные модели слишком громоздки для решения задачи анализа виброакустических процессов в трубопроводах. Известна конечноэлементная модель динамики трубопроводов сложной пространственной конфигурации с пульсирующими потоком рабочей жидкости, созданная на базе использования программного комплекса ANSYS [1-2]. Недостаток данной модели заключается в ее высокой трудоёмкости. Указанный недостаток данной модели устранен в математической модели [3] Существенное сокращение вычислительной трудоемкости достигается при рассмотрении трубопровода с точки зрения механики стержней [4].

В настоящей работе разработана конечноэлементная модель, позволяющая рассчитывать в безразмерных параметрах виброакустические характеристики пространственно сложных трубопроводных систем при их силовом нагружении пульсирующим потоком рабочей жидкости и кинематическом возбуждении со стороны присоединенных агрегатов и систем.

де конечных элементов (МКЭ), т.к. метод конечных разностей (МКР) считается недостаточно эффективным и в значительной мере устаревшим. МКЭ по сравнению с МКР требует меньше машинных ресурсов (меньше оперативной памяти), расчет идет быстрее (меньше затраты процессорного времени), результат расчетов более адекватен. Преимуществом конечноэлементной модели перед конечно-разностной является также возможность внедрения разрабатываемых конечных элементов в современные универсальные CAE-системs, такие как Ansys, Nastran, Patran, Cosmos и др. что позволяет расширить их элементную базу, а также в частности решать задачи моделирования виброакустичес-ких характеристик трубопроводных систем с пульсирующим потоком рабочей жидкости в комплексе с анализом динамической нагружен-ности присоединенных агрегатов и систем, анализом технического объекта в целом.

Система уравнений, описывающая малые колебания пространственно криволинейных трубопроводов с осевой линией, лежащей в одной плоскости, при их силовом нагружении пульсирующим потоком рабочей жидкости и кинематическом возбуждении со стороны присоединенных агрегатов и систем записывается в виде [3]:

1 д u u 2 =— — ,

Х з ^d e

2 6 ² u 1     д ⁴ u 1

^³ St ²    де²дт ²

д⁴ u,            ₂

- nw ^T-- ^nWХ з де от

д ² u 1 дедт

-

SUj 1

д е ⁶

-

( p + nw ² +

2 х ² г' ^{Х з} )д е ⁴

-

^ (1)

-

Ф з =

\ _{2    4}\д² U,         ₂ д w

) Хз ⁺ Хз ) —т = nwX 3 — д е         д т

1 д ² и 1

Х з ^{д е 2}

⁺ Х з u 1

д w

-

nw , д е

где 8 - безразмерная координата, отсчитываемая вдоль линии центров тяжести сечения трубопровода от начала отсчёта до некоторого произвольного поперечного сечения; т - безразмерное вре

мя; n = —m^² —; m .(s ) - погонная масса трубо- m 1 + m₂

провода; m₂ ( s ) - погонная масса рабочей жидкости в трубопроводе; c₃ – кривизна осевой линии в плоскости, перпендикулярной e ₃ ; e₃ ( s,t ) - единичный вектор, направленный по бинормали к осевой линии трубопровода; e 1 ( s, t ) – единичный вектор, направленный по касательной к осевой линии трубопровода; ё₂ ( s,t ) - единичный вектор, направленный по нормали к осе-

вой линии трубопровода; l – длина трубопровода; w – вектор безразмерной скорости рабочей

жидкости; p – безразмерное давление; u₁ – виб роперемещение в направлении e 1 ( s,t ) ; u₂ - виб роперемещение в направлении e _] ( s,t ) .

Выражения для мгновенных значений коле

-

-

-

бательных составляющих давления и скорости рабочей жидкости в рассматриваемом случае гармонических колебаний в безразмерных величинах давления и скорости рабочей жидкости,

представлены в виде (в левой части приведенных ниже равенств - безразмерные величины, а в правой – размерные, кроме t ):

ными производными заменяется системой обыкновенных дифференциальных уравнений [5]. Полученная система решается повторной дискретизацией по времени.

Аппроксимация uˆ ₁ для решения u₁ с помощью метода частичной дискретизации записывается в виде:

м - 1

u i * u i = Z ° -^{( T} ) ^N. ( ⁸ ) ,     (3)

m = 0

где N m ( 8 ) – базисные функции. При этом N m ( 8 ) не обязательно удовлетворяет всем краевым условиям.

Аппроксимирующее уравнение по методу взвешенных невязок в общем виде записывается:

J WRQdQ +J WRdF = 0,(4)

Q du1d где Rq = Lu1 + P —^™: P , 2 - невязка апп-dTdT роксимации по области, RF = Mu1 + r - невязка аппроксимации в краевых условиях, Wl ,Wl -линейно независимые весовые функции.

С учетом приведенных соотношений перепишем второе уравнение системы (1) в виде:

2 n fl ( 1 - 8 )

cos2

*т ) =-- C^^o¹» ^;*‘₁‘т I

'У*      АззA33

cos——      33 V ’

Г d⁶Z/j /           2 T 2 ^3⁴Z/j

J (^-6- + ⁽ p + nw + ² Х зо ) ^-4- +

^ d s                  d s

О u 1 d s ²

₂ d w ^nw Z 30 — ⁺ OT

. 2f ( 1 - 8 ) sin

/ \ _c    pj m , + m₂ . _„₂ m , + m₂

wst) =-----C^^-вх- —---2 sin 2nfl —-т

V ’ 2f  pc\ A„ cos—~       '    33 V '

d w    ₂ d ² u     d ⁴ u

+ nw--x30 —2" +--2—2 + ds дт2 ds 2дт2

d u, + nw--;-- ds ³дт

d ² z/.

⁺ nW % 30^^L)Wl^{d s} = ⁰ dsdT

Данные выражения справедливы только до частот, ниже частоты первого акустического четвертьволнового резонанса, когда колебания всех частиц невязкой жидкости в стоячей волне происходят софазно.

Рассмотрим схему решения второго уравнения системы (1). Данное уравнение является линейным нестационарным дифференциальными уравнением. Его можно записать в общем виде [5]:

du     d 2 u

L^U 1 ⁺ p ^- a--- P —1 = 0 , на Q , (2)

d T     d T

Используем аппроксимацию по Галеркину. В этом случае вместо привлечения новой системы функций в качестве весовых множителей выбираются сами базисные ф у нкции:

W l = N l и W l = - N l на F .

Подставим аппроксимацию uˆ ₁ в уравнение (5) и запишем полученную систему дифференциальных уравнений в векторной форме:

[ M ] ^ d 2 ^ ^ l + [ ^c ] ^ dU l + [ K ][ U ] = [ f ] ;     (6)

T                       т

Здесь компоненты отдельных матриц и правой части определяются равенствами:

где L – линейный оператор, включающий дифференцирование только по пространственным переменным, p, a , P - заданные функции координат и времени, Q - пространственная область.

Для решения данного уравнения применим метод частичной дискретизации, при котором исходное дифференциальное уравнение с част-

Mim = 11 d^Nm - X3oNm INids 0 V ds

C im = h- w f d 3 N m + z 30 dN m 1 Nd s

0 V ds3

1 f d6N               d4N

^K m = fl —pr ^{+ (2} Х 2о ⁺ P ⁺ nwHH m ⁺

0 V ds

, d2N     .

■+ (Хзо + P + nw )Хзо    m INlde de J

N =— ^—43 ( § ⁶ — ^— § — ¹⁰ § ⁴ + ²⁰ § ³ + ² § 2 — ^— § ).

¹      40      3     9     27     9     27   ;

, г    Id w    5 w 1

^f l = ⁿ X 30 H-- ^w ^- I ^N l ^{d e} 0     V0T    8e J

В общем случае аппроксимация uˆ₁ на эле менте с P + 1 узлами будет сводится к многочле ну степени p . На таком элементе узлы которо

-

-

-

N 4 =

N e =

N 3^e

243   6 H§	— 2 § 5 — 3	23 § 4 9	+ 23 § 27
81 6 — —( § "	- 24 § 4 + 9	^§2 81	— 4). 81 ;
243    6 :-----(§ 16	+ 2 § 5 • 3	- 23 § 9	4 13 ^^^^^^^^^b 27

§ + ⁴ § + — §);

9     27   ^;

:³ + 22 § 2 — ^— § )■

27     27   ;

го с номерами от 0 до p помещены в точки е ₀ , e_f , е₂ , ^, e_{P — f} , e_P , ассоциируемая с узлом l . Базисная функция элемента N_l будет многочленом степени p , принимающим значения нуль во всех других узлах элемента.

N‘ =_— ²⁴³( § ⁶ ₊ ^— § _— ¹⁰ § 4 _— ²⁰ § ³ ₊ ² § ² ₊— § ) •

⁵      40      3     9     27     9     27   ;

В уравнение (5) входит производная 6 поряд ка. Следовательно, для получения точного реше ния базисные функции, входящие в аппроксима цию должны иметь 6 порядок или выше. Это не

-

-

-

-

обходимо для выполнения требования полноты системы базисных функций, позволяющей им с любой степенью точности аппроксимировать неизвестную функцию [5]. В качестве базисных функций удовлетворяющих данным условиям возьмем многочлен Лагранжа степени p = 6 [5] N e = 4 = ^{[( e —} e X ^{е —} e )”( ^{e - e} i - 2 X ^{e — e} i + 2 )-( ^{e — e} p ^{)] x x [( e} i ^{— e} o X ^e l ^{— e} f ХД ^ ^{— e} i - f X ^e l ^{— e} i + f ) •" ( ^e i ^{— e} p ^)]

Запишем базисные функции для одного се миузлового элемента. Выразим их через норми рованную локальную координату § , определя емую равенством:

-

-

-

§ = 2( е — е_с) h^e

.

Здесь е^е_с - координата центра элемента, h e – длина элемента. Элемент принадлежит отрез-

ку — 1 <  § <  1 :

N e = 8L( § ⁶

0   80

^^^^^^

§ 5 — ⁵ § ⁴ + ⁵ § ³ + ^— § ² — ^— § );

9      9      81      81    ^;

N e = 8²( § ⁶ + § 5 — 5 § — 5 § + ^— § ² + ^— § )

⁶   80             9      9      81      81    ^.

Полученные базисные функции представле ны на рис. 1.

Запишем систему уравнений (7) через нор

-

-

мируемую локальную координату § . Получим:

M m = J |

- f

2 d²N„    ₂ h e    1

--m — Хз   N„ I Nd e h d §     ³⁰ 2 ^m J ^l

/

V

1 2^

i d§³

+ X²» — ^J Nde •

³⁰ d § J ^l ’

= f ff 2 1 5 ^d6N _f + .2_Z, + р + nw)2 1 ' ^dN + (И)

m J ( he J de^{6    3030}       \K) de^{4     (} )

V

²      1

■ + (Z* + P + nw )X_M I   I d—f-

^{30 F      ,Л30} ( h e J d e J

N l d e ;

.

1    Idw    5 w 1 he f= nX30 H— w^- hr Nld§ 0     V 5т     tie J 2

Систему уравнений (11) будем решать мето дом базисных функций. Для представления вре менной области, которая считается продолжаю

-

-

-

щейся до бесконечности, используем конечные элементы. Условия на конце первого элемента определяются с помощью дифференциального уравнения и начальных данных. Затем этот про-

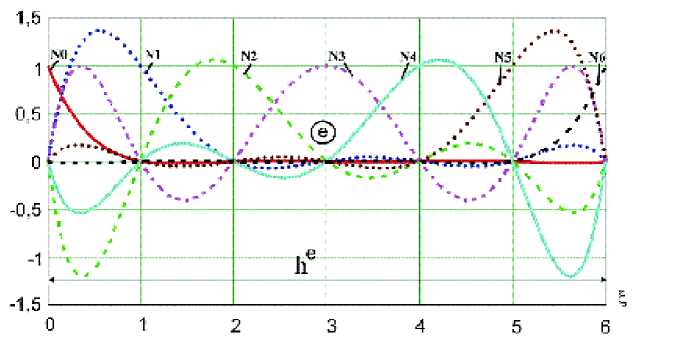
Рис. 1. Одномерный элемент и ассоциируемые с ними стандартные базисные функции шестой степени

цесс повторяется для последующих элементов с использованием вновь вычисленной информации в качестве начальных данных для каждого очередного элемента. Пусть да a «a _£tt„Nm(T) .         (12)

m _ 1

Базисные функции N _m ( t ) должны иметь степень не ниже второй, так как в уравнение (6) входят вторые производные по времени.

Возьмем типичный квадратичный элемент n по времени с тремя узлами, помещенный в точки ^T 2n - ^T 2n + 1 - ^T 2n + 2 (см. Рис. 2, 3).

На этом элементе n имеем a = a2-^ + a2+1Nnn+1 + a2n+2Nnn+2. (13)

Тогда как все остальные базисные функции на элементе n равны нулю. Здесь

[ м+YWt n ) + PtKA n ) R n " ² +

+ [ - 2 M +(1-2^0^ ) _ЧШ-2р+_УХ KAt „ ) ] a ² ^ + ₍₁₆₎ + [ м-Ц-.-^ б сСХб», ) + (1/2 + p-y)At n K(At n ) Ь ^{2 n} _ f n At n

Интерполируя f тем же самым способом, что и a , получим fn _ Pf22+2 + (1/2—2P+Y )f2n+1 + (1/2+P—Y )f2n .(17)

Рассмотрим частный случай краевых условий – жесткую заделку концов трубопровода. В этом случае при £ _ 0 и £ _ 1 u1 _ u2 _ 0 . Тогда из первого уравнения системы (1) следует, что d u1 d£

0 , а из третьего уравнения d 2u, ”£?

_ 0 . Опу-

стим индекс 1 у параметра u .

Для рассматриваемой конечноэлементной модели граничные условия можно записать в виде

N _ - T(1 - T) , dN^ _ — 1/2 + T .

2n 2      ’ dT Atn ’ d2N2n _ 1 n        2 dN2n+1 __ 2T dT2    Atn ; N2n+1 =1 T ; dT      Atn ’

M _ 1

2 U_m _ 0

m _ 0

m — 1 d U

2 m _ 0 при £ _ 0 и £ _ 1 .    (18)

m _ 0 ^d£

M ^-1 d^ U m

² 0 Bs²

_ 0

d2N”nn ___2_      _t( 1+T). dN2n+2 __ 1/2+T dT2     д2 ’ 2n+2     2 ’ dT        Atn d2N2n+2 _ 1 T _ t — t2n+1      _    _     .

d T ²       A t n ^;         A t n   ’ ^{A t}n ^_T 2n + ^{2 T} 2n + 1 ;

^{A t}n ^T 2n + 1 ^T 2n

Распишем последние два уравнения системы (18), подставив в них аппроксимацию (3) и учитывая, что перемещение в узлах на границе a₀ и a₆ , а также базисные функции N₁ , N₂ , N₃ , N₄ , N₅ в граничных точках равны нулю a₀ _ 0 и a₆ _ 0 , получим

Применение к уравнению второго порядка (6) стандартного метода взвешенных невязок дает

2n + 2

2ˆ         ˆ f M + C— + Ka _ f W„dT _ 0. (15)

T n ( d T ²     d T ^J) ⁿ

T

, 2 + + 2

n _ 0,1,2,...

Здесь интегрирование производится только по элементу n , поэтому в полученном выражении можно подставить для aˆ значение (13). Учтем, что матрицы C и K зависят от времени. Тогда в силу (14) уравнение метода взвешенных невязок после соответствующих преобразований принимает вид

0          1          2          3          4

в---•---e---•----e•—

T,=0       T,         T,         7,         7,T,

I CD I CD I CD

• - внутренние узлы элементов, О - граничные узлы элементов

Рис. 2. Разбиение временной области на квадратичные конечные элементы

5 ^ 1 (0)      5 N 2 (0) ,    5 N ₃ (0) ,

Mi             a о

1    ^           2    ^3

08        0808

5 N (0)     5 N (0) _n

+ a    4/-^J- + a. — _ 0

4  58     5

5 N (1)     5 N (1)     5 N (1)

a 1   +a 2   +a 3

58       585

5 N (1)     5 N (1) _n

+ a4   4^ + a._

4  58

5 ² N , (0)      5 ² N 2 (0)      5 ² N 3 (0)

a ¹ 5 8 ^{2 +} a ² 5 8 ^{2    +} a ³ 5 8 ^{2 +}

52 N (0)    52 N (0)

+ a₄---- 4г^ + a=, ----5r^ ⁼ 0

4   582      5

5 ² N (1)      5 ² N (1)      5 ² N ₃ (1)

1—2-^-3-^- aaa

1 582      2 5823

5X0)   5 X 0) _₀

aa

4   582      5

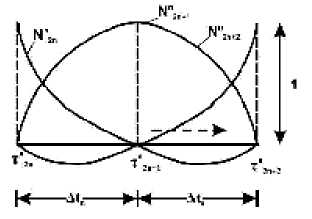
Рис. 3. Базисные функции элемента n

зации по времени At = —. В качестве начальных данных в рассматриваемой трехслойной схеме для начала вычислений требуются начальные данные, которые задаются в виде da

a( T = 0) = a⁰ = 0 , "^(t = 0) = 0 .    (21)

Для определения a¹ применим стартовую ко-

Таким образом имеем 4 уравнения и 5 неизвестных величин a ₁ , a ₂ , a₃ , a ₄ , a₅ . a₃ находим из уравнения (6), которое для случая одного элемента можно записать в виде

[ М зз f dU !• [ ' ■"f dU 1+ [ KU ] = f ] . (20) d r J d T J

Необходимо отметить, что изменение граничных условий не приводит к перестройке конечноэлементной схемы решения. Выражения (11) для внутренних узлов элемента остаются прежними. Изменяется только вид уравнений системы (19), описывающих граничные условия. В конечно-разностной модели изменение граничных условий приводит к перестройке схемы решения, что увеличивает трудоемкость получения результатов расчета по сравнению с предложенной конечноэлементной моделью.

В качестве модельного примера возьмем трубопровод со следующими параметрами: l = 0,4м ; d = 0,004м ; 5 = 0,0006м ; p = 7800кг / м³ , E = 2 • 10¹¹ Па ; R = 0,23м ; где d - наружный диаметр трубопровода, 5 - толщина стенки трубопровода; R – радиус кривизны.

Предположим, что в начальный момент времени деформация трубопровода отсутствует и он находился в состоянии покоя. Затем трубопровод нагружается установившимися колебаниями рабочей жидкости в которой реализуется стоячая волна с параметрами f = 250Гц, р х = 10 5 Па. Характеристики рабочей жидкости: Р ж = 870кг/м³ , с = 1300м/с.

При проведении расчётов возьмем один семиузловой элемент и постоянный шаг дискрети- da a - a нечно-разностную схему —- =------ dt     At

, где i – со-

ответствующий временной слой.

Для того, чтобы полученная схема была безусловно устойчивой необходимо, чтобы значения в и Y удовлетворяли условиям