Конечноэлементное моделирование усталостной прочности композитного материала

Введение. Прочностные и жёсткостные свойства несущих элементов из полимеркомпозитных материалов в процессе эксплуатации снижаются до опасных значений. Прогноз ресурса таких элементов имеет большое практическое значение. Однако в настоящее время данная проблема не решена. Изменение прочностных и жёсткостных характеристик полимеркомпозитных лонжеронов несущего винта вертолёта связано с несколькими факторами: циклические нагрузки, воздействие окружающей среды (например, эксплуатация в условиях высокой влажности [1]) и др.

В работах, посвящённых этой теме, описываются результаты построения кривых усталости на основе экспериментов [2, 3] и моделирования этих свойств — например, конечноэлементного [3, 4]. Современные конечноэлементные программные комплексы позволяют проводить расчёты на усталостную прочность конструкций. При этом усталостные свойства составляющих их материалов должны быть известны. Однако иногда соответствующая информация о компонентах композитов отсутствует, поэтому требуются либо дополнительные эксперименты, либо решение обратных задач для идентификации этих свойств на основе кривых усталости композита. Отдельной проблемой является моделирование интерфейсных слоёв между матрицей и армирующим волокном [5, 6], особенно при наличии повреждений.

В работе рассматривается композиционный материал, усиленный однонаправленными нитями. В ANSYS Workbench с помощью выделения представительного объёма материала рассчитывается усталостная прочность. Проведены две серии расчётов. Первая — для модельного материала, вторая — для полимеркомпозита, полученного термическим отверждением эпоксидного связующего, усиленного стекловолокном. Диапазон напряжений выбран с учётом характерных нагрузок на лонжерон лопасти несущего винта вертолёта. Получены зависимости числа циклов безотказной работы от интенсивности нагрузки.

Работа выполнена при частичной поддержке РФФИ (гранты 10-08-01296-а, 10-01-00194-а, 10-08-00093-а).

Постановка задачи. В рамках линейной теории упругости [7] рассмотрим композиционный материал, армированный однонаправленными нитями (рис. 1, а), и его представительный объём, содержащий один армирующий элемент (рис. 1, б). Будем считать, что армирующие нити и мат- рица жёстко сцеплены.

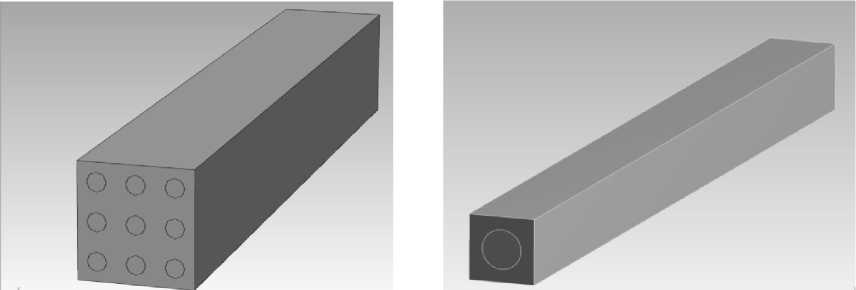
а )                                                        б )

Рис. 1. Армированный композит и его представительный объём

Один торец элемента (рис. 1, б ) жёстко закреплён. На другой действует равномерно распределённая нормальная нагрузка, характерная для эксплуатации рассматриваемой конструкции. На боковых поверхностях задаются условия гладкого контакта. Усталостный расчёт проводился при многоцикловом растяжении-сжатии. Характер нагружения — симметричный. Использовался основанный на эмпирических S-N -кривых SN- метод [8] (в конечно-элементном пакете ANSYS WorkBench). Выбор данного метода объясняется следующим обстоятельством. Он изначально разрабатывался для описания многоосного напряжённого состояния. При этом предполагается возможность получить амплитуду напряжения симметричного цикла нагружения, эквивалентного по повреждаемости с данным асимметричным циклом нагружения в случае, если главные оси тензоров напряжений амплитудных и средних значений напряжения цикла не совпадают. Примером может служить случай симметричного цикла кручения при постоянном изгибе и т. п. В пакете ANSYS WorkBench также возможно провести расчёт по методам Goodman, Soderberg, Gerber.

Таблица 1

Напряжения усталости для стали

№	Cycles	Alternating Stress (Па)
1	10	3999000000
2	20	2827000000
3	50	1896000000
4	100	1413000000
5	200	1069000000
6	2000	441000000
7	10000	262000000
8	20000	214000000
9	100000	138000000

Численные результаты. В качестве тестового примера рассмотрены композитные материалы, усталостные кривые которых имеются в стандартных библиотеках программного комплекса ANSYS Workbench, — это конструкционная сталь (армирующие волокна) и алюминий (матрица). Соответствующие напряжения усталости из стандартной библиотеки комплекса представлены в таблицах 1 и 2. Модуль упругости и коэффициент Пуассона: для стали — ν = 0,3, для алюминия — E = 7,1·10¹⁰ Па, ν = 0,33.

Таблица 2

Напряжения усталости для алюминия

№	Cycles	Alternating Stress (Па)
1	1700	275800000
2	5000	241300000
3	34000	206800000
4	140000	172400000
5	800000	137900000
6	2400000	117200000
7	55000000	89630000
8	100000000	82740000

Сетка конечных элементов с упорядоченным разбиением представлена на рис. 2. Тип элемента — 4-узловой тетраэдр, размером 10–6 м. Количество узлов — 74089, элементов — 14922.

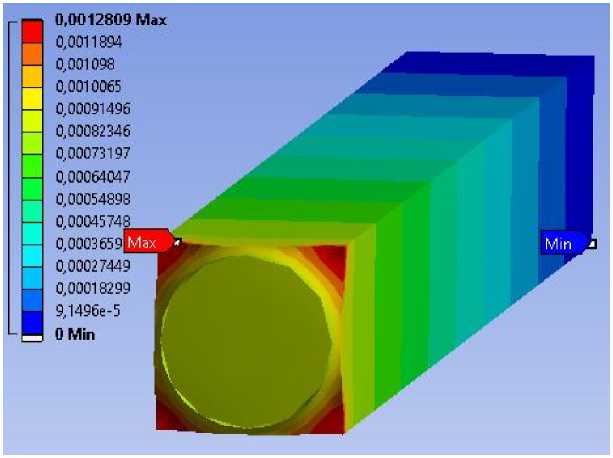
Рис. 2. Сетка конечных элементов и распределение эквивалентных напряжений (по Мизесу), полученных в результате статического расчёта

Рис. 3 иллюстрирует результаты расчёта усталостных кривых тестового композиционного материала. Рассмотрим рис. 3, а . Здесь горизонтальная ось — коэффициент нагружения, вертикальная ось — количество циклов до разрушения. Горизонтальный участок кривой — область не-накопления повреждений (1 на горизонтальной оси здесь и далее соответствует приложенному напряжению 250 МПа). На рис. 3, б , горизонтальная ось — число циклов до разрушения, вертикальная ось — амплитуда приложенного напряжения. Кривая композитного материала (треугольные метки) находится между соответствующими кривыми для армирующего волокна (квадраты) и матрицы (кружки).

Основная цель работы — изучение усталостных свойств полимеркомпозитного материала, используемого в вертолётостроении для изготовления элементов конструкций — таких, например, как лонжерон лопасти несущего винта. Такой композитный материал состоит из стекловолокна (армирующий материал Е = 8,7·10¹⁰ Па, ν = 0,22) и эпоксидной смолы (матрица Е = 2,55·10⁹ Па, ν = 0,22). Расчёты проводились для двух моделей с процентными соотношениями матрицы и волокна 35 % : 65 % (технологическое требование к композиту) и 50 % : 50 %. Кривые усталости (аналогичные рис. 3) представлены на рис. 4, 5.

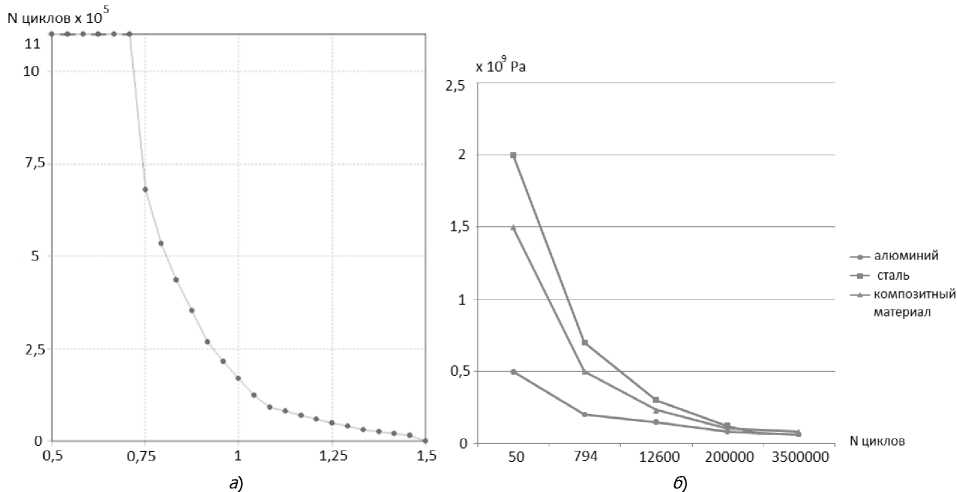
Рис. 3. Кривые усталости композита

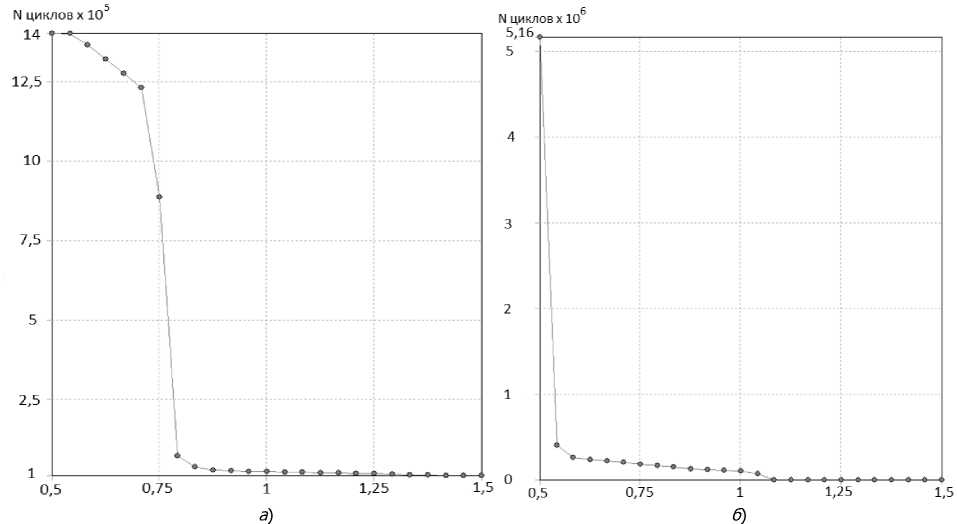
Рис. 4. Кривая усталости композита с соотношением матрицы и волокна: 35 % : 65 % ( а ); 50 % : 50 % ( б )

Анализ кривых усталости, представленных на рис. 5, позволяет сделать следующее заключение. Нарушение технологических требований по процентному содержанию компонентов полимеркомпозитного материала существенно (на 25—40 %) снижает ресурс долговечности конструкции.

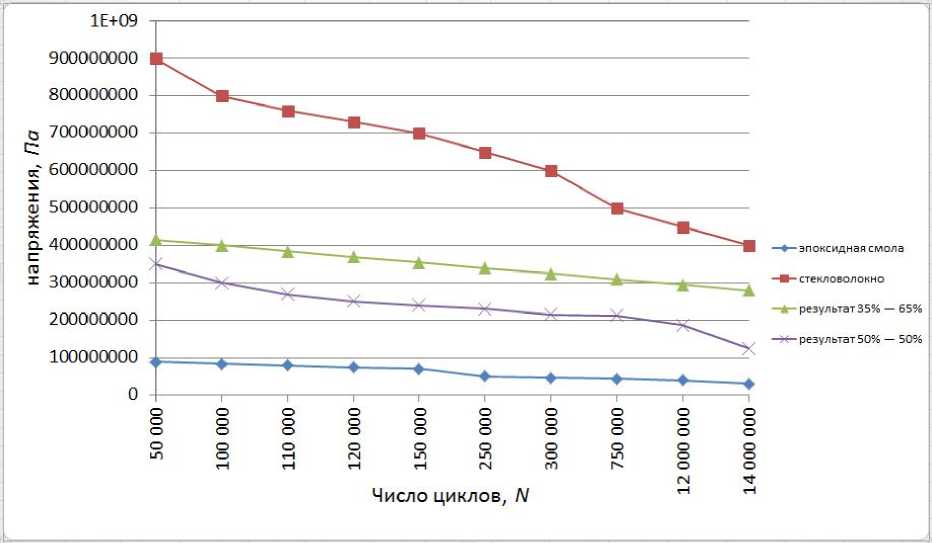
Рис. 5. Кривые усталости полимеркомпозитов

Выводы. Предложена методика расчёта усталостных свойств композитных материалов. Она основана на конечноэлементном моделировании представительного объёма материала, находящегося в напряжённо деформируемом состоянии, соответствующем эксплуатационным условиям. Задача определения многоцикловой усталости решена с помощью пакета ANSYS, в котором имеется соответствующий модуль. Проверка предложенного метода на тестовом примере доказала его работоспособность. С помощью данной методики рассчитаны усталостные свойства полимер-композитного материала, используемого в вертолётостроении. Результаты расчёта позволяют оценить изменение исследуемых свойств при нарушении технологических требований к процентному содержанию компонентов композита. Представленная методика может служить основой для определения ресурса долговечности элементов вертолёта. Дальнейшее развитие метода определения ресурса долговечности связано с учётом климатических условий эксплуатации, воздействия влажности и температуры.