Конечные деформации в задачах формообразования неупругих тел

Предложена математическая модель, основанная на трех группах уравнений: геометрические соотношения связывают логарифмический тензор деформаций Генки с век тором перемещений; соотношения ассоциированного закона пластического течения, устанавливающего соответствие между приращениями тензора Генки и тензора напряжений Коши; вариационные уравнения Лагранжа и вариационные неравенства для Формулировки граничных условии.

Модель реализована на ЭВМ с использованием метода конечных элементов <МКЭ> и шагового метода ио нагрузке с внутренним итерационным циклом. Решены конкретные задачи исследования реальных технологических процессов обработки Сталлов давлением.

1.    Построение математической, модели процесса Формообразования неупругих тел

Для построения математической модели, описывающей поведение тел при конечных неупругих деформациях, всесторонне исследованы свойства тензора деформации Генки. В частности, доказаны следующие его свойства: ^

• 1.    Производная от тензора Генки по Яуману-ноллу h совпадает с тензором деформации скорости d, в частности, для малых деформаций и конечных перемещений, а также в случае соосности тензоров h и d для произвольных деформаций:

• 2.    Разбиение h на сумм',' упругой he и неупругой hp составляющих вытекает из разбиения тензора d на соответствующие составляющие. Указанные суммы согласуются с введенным Ли представлением тензора-градиента места в вид-■ скалярного произведения тензоров-градиентов, ответственных за упругую и неупругую деформации, при условии, что чгнзор жесткого поворота будет в

• 3.    Тензор Генки связан с тензором £ ,обратным тензору Ал' манси, зависимостью:

• 4.    Компоненты приращения тензора Генки можно определит.-, i > компонентам метрического тензора gnsCg^ns> из соотношения:

h^ - h 4 hZto - ‘■'•h = Л . (1 ) где ш- спин тензора d

первом множетеле этого произведения.

[ ²’^?       (2*f. ^4 . . . Н Г⁺¹ (2-^            .   (2)

дн = ДЯ^ ^ л^п -4а я¹ f ^J-O g^k(T) dr . О) тогда

-i

Я = Д v-h (R7) + ДЯ .                                 (4)

i де t>T ~ пределы изменения времени протекания процесса; Я вектор-радиус положения точек тела в конечном состоянии; V векторный оператор Гамильтона.

Определяющие соотношения, конкретизирующие поведение мат» риала, записаны в предположении выполнения требований принципов материальной объективности,изотропии,второго закона термодинамики и выглядит следующим образом:

р Р ' t - о М h. ;   4 Р р k I ; й = 2 М X и У— f у ;

о                           р              dh'

■де t,L • тензор напряжений Ко^ци и его девиатор; It инвариант тензора; о - плотность материала; р,к - упруг рактеристики;

. ^д/         ' ГI               1        1

• 2 р X = —=- - ; d | | —*—,---: а I ;

dh ^l1 dh dh ^j J e              e p

(6 ;

• I.    если ,=0 и /<0

О, если /<0 или f^C и f<0, f - поверхность нагружения, которая, например, для условия зеса может быть определена соотношением:

11 *

/ = -у а а - * ; (a = ppt-gh).(7)

X>g экспериментально определяемые функции, ответственные изотропное и трансляционное упрочнение.

При вариационной Формулировке задачи в качестве воздейств^ на тело в конечном состоянии <К-состоянии> выбраны t и 7 t, реакциями на них с. чужат сао лете твенно v XI и У. Пластическая составляющая тензора деформации Генин, характеризующая внутреннее состояние тела, не включалось е число параметров состояния-определяющие уравнения записывались как дополнительные соотношения.

Для реализации решения задачи •использовался шаговый метод по нагрузке (нагружение в частном случае может осуществляться заданием перемещений) с внутренним итерационным циклом уточнения решения нелинейных задач на каждом шаге нагружения.

Дополнительная трудность в организации вычислительного процесса при исследовании конечных деФор -аций состоит в том, что конфигурация тела в К-состоянии, для которого становится справедливым вариационное уравнение, остается неизвестной. Эта конфигурация известна лишь для начального состояния, а далее на каждом шаге нагружения должна быть определена. Исходя из этого возникла необходимость преобразовать вариационное уравнение к метрике (конфигурации) некоторого промежуточного состояния. В начальном приближении таким состоянием является исходное.

Использование известного из геометрии правила преобразования ориентированных площадок, закона сохранения массы, а также предположение о том, что любая тензорная функция промежуточного состояния (П-состояния) отличается от своего значения в конечном состоянии на некоторое приращение, позволило вариационное уравнение привести к метрике П-состояния:

J t:V бу d.V - | t 611 = f V и-'*'®, vr бу dV у               о              ч

(8 >

• - f _t V          v )6И &о .

Здесь' ' т - тензор четвертого ранга, зависящий от свойств материала и накопленных деформаций; ь - единичная нормаль к пс верхности тела; у,со - объем и поверхность тела; t - векчиор напряжения на его поверхности.

* Структура уравнения QP такова, что в правую его часть перенесена "невязка" решения, которая стремится к нулю, если итерационный процесс сходится В процессе итерации производится корректировка искомых Функций. Равенство нулю правой части уравнения (s> говорит о том, что тело находится в равновесии в найденной конфигурации.

Предложен алгоритм, с помощью которого можно реализовать решение задачи, используя процедуру шагового метода с внутренним итерационным циклом. В отличие от широко применяемых традиционных разработанных алгоритм, основанный на подходе Лагранжа к описанию движения, позволяет в конечном итоге определить конфигурацию тепа и другие необходимые Функции «-состояния. Последнее утверждение следует из того, что вариационное уравнение справедливо для К-состояния, хотя для удобства реализации реше- ния з.-дачи оно приведено к метрике П-состояния.

Большую сложность при составлении алгоритма решения задачи вызывает учет реальных граничных условии. Наряду с простейшими (жесткая заделка, шарнирное опирание, свободная от кинематических связей граница) использованы граничные условия, обеспечивающие выход поверхности детали в процессе ее нагружения из-под поверхности прижимного устройства с трением и без него. Предусматривается возможность деформирования тела в пространстве,or— раниченном матрицей (пуансоном). При этом на каждом шаге нагружения определяются точки и моменты касания поверхностей детали и матрицы (пуансона) путем решения системы алгебраических уравнений, описывающих поверхность матрицы (пуансона):

?(?W) = О                       (9)

и вектор перемещения ио/ дГД?> - прямая, заданная в параметрическом виде:

х^^х1^!);    х^=хг*Х?Т);      ^=х3 кХ^Т) .

mm  m

Параметр т) позволяет определить момент пересечения вектора перемещения с поверхностью матрицы. Критерием пересечения является условие: т) е [0,1].

формулировка граничных условий при выходе точек тела на поверхность матрицы (пуансона) базируется на вариационном неравенстве:

эз зс< а

V к t - Т )• (6U_a + 6U_gv ) dw > О .   (11 )

me т - напряжение трения на границе контакта ш . Это напря- жение связано заранее известным законом с Физико-механическими свойствами контактирующих поверхностей и нормальным давлением.

Из неравенства (Jf), nepetликающегося с вариационным уравнением (д), вытекают следующие условия:

з                        з           эз

3           33

У = О => t < О;

U <  О на o>_t ; У < О => t = О;

за а           э t - т < О => У = О;

эа а          а      эа а t - т > О => У = О. t = т .

где индекс а относится к координатам, лежащим на поверхности тела, а "3" - к координате, ортогональной этой поверхности.

Варианты <12> граничных условий включают в себя различные случаи движения тела относительно поверхностей, ограничивающих пространство деформирования: "прилипание" точек тела к поверхности, скольжение с трением и без него, выход точек тела из контакта с поверхностью.

Запись вариационного уравнения <в> в тензорно-операторной Форме с выделением в явном виде вариации основной переменной би и градиента вектора перемещения V U, а также известное соответствие между матричной и тензорной записями математических соот ношений позволили Формализовать переход от к матричной записи уравнений, традиционной для МКЭ.

Для осуществления подобного перехода использованы изопара-метрические конечные элементы, характерной особенностью которых является то, что для них основные Функции, описывающие конфигурацию тела и поле перемещений, аппроксимируются одними Функциями Формы.

Суммирование по элементам всей конструкции осуществлялось поиндексно, как и в случае суммирования по неизвестным координатам (повторяющимся индексам) в тензорных соотношениях.

В качестве примера, иллюстрирующего упомянутые преобразования, 'приведем выражение для одного из входящих в уравнение слагаемых:

q р <11 П its 'j> 1

f VU “V^SXJdY =Ssw Vv? f Й_ЬФ 1 я$ , Й 5 1 dV. (13)

J z3 ) I k J . nl t s J • ¹ '

4*

где S - узловые перемещения в направлении координаты F ;

                                                       ke аппроксимирующая Форма для l-того узла: »$  - Физические

<4> ненты тензора щ в рассматриваемом системе координат;

q

Ф -

компо-

9   - к

оператор, связанный с ковариантной производной от тензора. Индексы, взятые в скобки, относятся к узловым точкам системы конечных элементов и по ним производится суммирование по всей совокупности узлов. Остальные индексы характеризуют тензорный признак Функции, и суммирование по ним производиться по обычным правилам тензорной алгебры.

В частном случае матричные уравнения записаны для декартовой ортогональной и цилиндрической систем координат.

2.Численная реализация решения задачи на ЭВМ.

На основе составленой математической модели написана программа, базирующаяся на МКЭ. Программа позволяет исследовать процессы деформирювания тел в пространстве, ограниченной матрицей (пуансоном), с различными, в том числе и изменяемыми е процессе деформирования граничными условиями, с учетом сил трения и начальных напряжений. Для решения задач с использованием этой программы в качестве исходной вводится в ЭВМ следующая информация: -

Е форма исходной заготовки и ее разбиение на конечные элементы с заданием координат узловых точек. Возможно применение конечных элементов с различным количеством узлов, тем не менее за базовый выбран 9-узловой изотропный лагранжев конечный эле-

• 2-    Ферма рабочих поверхностей матриц, пуансонов и прижимных устройств. Они могут вводиться б ЭВМ в виде совокупности координат точек поверхности или задаваться координатами характерных точек изменения кривизн и центров кривизн. Последний способ наиболее удобен для исследователя, так как позволяет брать характерные размеры первоначальной Формы поверхности матрицы (пуансона) непосредственно с чертежа детали.

• 3-    Нагрузка на заготовку задается ее значениями в поверх-ностйых узловых точках конечных элементов и в точках временного интервала, соответствующего границам шагов нагружения по времени. При нагружении заготовки через пуансон задается перемещение его характерной точки как Функция от времени. Перемеще

• 4.    Характеристики материала u,v, а также диаграмма его деформирования t для одномерного напряженного состояния. Диаграмма заноситься в память ЭВМ таблично (до 20 точек) и в дальнейшем аппроксимируется сплайн-Функциями до третьего порядка. Возможно задание диаграммы деформирования и в виде любой анали-тической зааисиное'• н.

• 5.    Коэффициенты трения материала заготовки о поверхности матрицы, пуансона и прижимных устройств.

ние остальных точег; -. вязано с заданием геометрии поверхности пуансона. Возможна гакже задание вектора перемещения любого количества узловых точек ^^чечно-элементной сетки.

Программа позволяет определить следующие характеристики процесса деФсрмировд.- шя:

• 1.    форма деформируемого тела и его напряжения и деформации в любой момент нагружения, в том числе в моменты, предшествующие требуемому отжигу на технологическом переходе, и в конечном состоянии,

• 2.    Величину нагрузки на тело и ее закон распределения по поверхности в любой момент нагружения.

• 3-    Форму рабочих поверхностей матрицы и пуансона, необходимых для получения детали заданной геометрии.

• 4-    Критическую нагрузку, соответствующую моменту исчерпания несущей способности. При задания перемещений точек деформируемого тела программа позволяет проследить за изменением НДС и конфигурацией детали в закритимеской области.

• 5.    Пружинение после снятия нагрузки на любой стадии нагружения дечэли

• 6-    Распределение остаточных технологических напряжений и даФормаций.

В качестье примера на рис.1 показана схема нагружения получаемого давлением полиуретана оживального конуса при его деформировании е пространстве, ограниченном сферической матрицей. Заданный закон распределения давления на поверхность заготовки обеспечивался постановкой в полиуретан поперечных металлических пластин. Нагружение осуществлялось таким образом, что нижний край оболочки оставался неподвижным, а верхний мог скользить но поверхности матрицы Последовательные положения оболочки при росте давления показаны на рис.1.

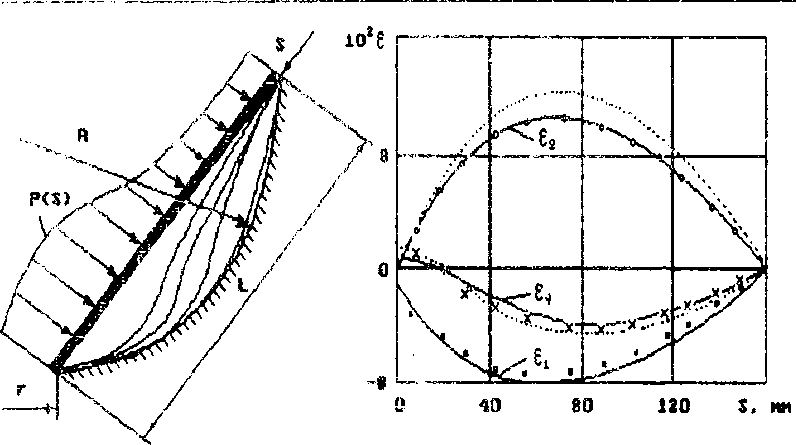
Рис. 1. Схема нагружения. Рис. 2. График распределения деформаций.

На рис.2 приведены графики распределения деформаций вдоль образующей Се^), направляющей t^) и по толщине оболочки ^у^" Пунктирами доказаны кривые, соответствующие расчету процесса по безмоментной теории с предварительным заданием характера изменения деформации с , диктуемого Формой поверхности матрицы.

Точками показаны экспериментальные значения деформаций, полученные путем сопоставления нанесенных на поверхность оболочки координатных сеток деформированной оболочки и исходной заготовки. Деформация с^ определялась по разности толщин.

Оболочка была выполнена из АМг-бМ <Е=6,8 104 МПа, t =165МПа р t =330 МПа, с =0,2). Диаграмма деформирования вводилась пото-ь 2

чеч^о и аппроксимировалась в ЭВМ сплайн-функциями. Размеры заготовки и матрицы <рис.1>: 1г=168 мм, R=164 мм, г=78 мм, 6_о=1,2 мм. Трение в расчете учитывалось, Ь =0.1.

тр

Некоторые результаты решения задачи стесненного изгиба панели < ширина 51,25 мм, толщина 1,2 мм, материал АМг-бМ ) при ее деформировании пуансоном в матрицу <их базовые размеры 20,6 мь и 23 мм соответственно) показаны на рис.3-5. Деталь получена за четыре перехода.

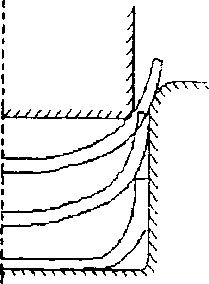
На рис.З показаны промежуточные положения детали на трех первых, а на рис.4 - на четвертом переходе, соответствующем стесненному вдавливанию стенки панели до полного заполнения ее материалом пространства между матрицей и пуансоном. В результате такого деформирования происходит существенное уменьшение растягивающих напряжении t на внешней поверхности панели вдоль 2

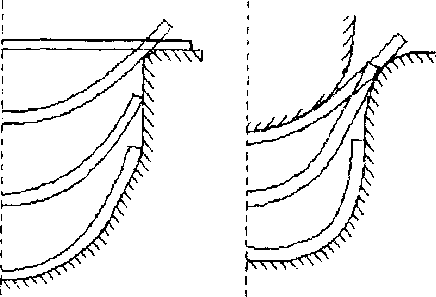
Рис. 3. Промежуточные положения детали на трех первых переходах.

направляющей. Это видно на рис.3, где показаны графики изменения t вдоль координаты внешней поверхности заготовки (номера точек на графике по координате Ь соответствуют номерам узлов на детали). Графики построены для различных положений детали (номера положений обведены на рис.4 и 5). Радиусы закруглений матрицы и пуансона на последнем переходе равны 1,5 мм.

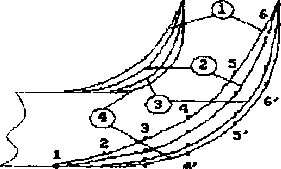
Рис. 4. Промежуточные положения детали на 4 переходе.

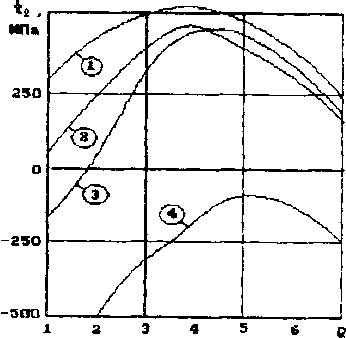
Рис. 5. График растягивающих напряжений.

Самареий авиационный институт