Конечные повороты оригинального манипулятора

В [1, 2] была описана сущность работы шестикоординатного манипулятора (пространственного механизма) и область его использования. Рассмотрим только оригинальную часть данного механизма (рис. 1).

X

Z

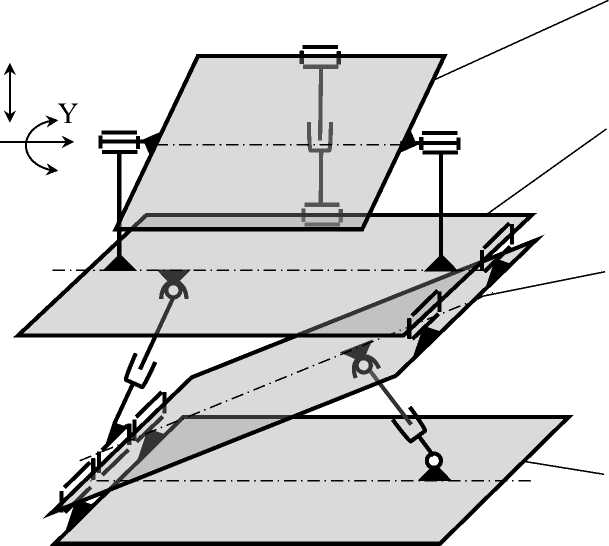
Рис. 1. Оригинальная часть пространственного манипулятора

Позиции на рис. 1: 1 - Поворотный стол; 2 - Наклонная платформа; 3 -Опорно-поворотное устройство; 4 – Рабочий стол.

Кинематику опорно-поворотного устройства 3 пространственного манипулятора будем рассматривать при произвольном перемещении поводков 2 и 3 (рис. 2 - 3). Для упрощения схемы, на рис. 2-3, не показаны опоры и выходное звено (рабочий стол). Черным цветом показано начальное положение механизма, синим цветом – при изменении длины одного поводка и красным цветом – при изменении длины второго поводка (конечное положение).

Позиции на рис. 2 – 3: 1 - Поворотный стол; 2 - Правый поводок

(двигатель поступательного перемещения); 3 – Левый поводок (двигатель

________________________________ 2 ______________________________ "Теория и практика современной науки"                №1(7) 2016

поступательного перемещения); 4 - Наклонная платформа; 5 - Опорноповоротное устройство.

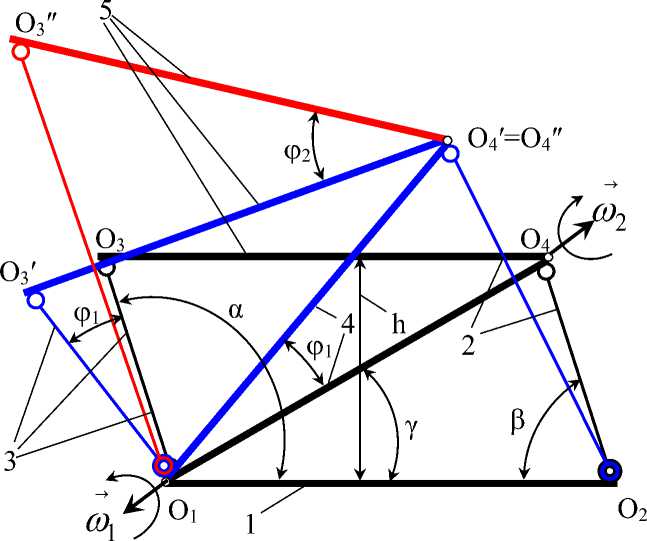
Рис. 2. Схема перемещения фрагмента манипулятора при движении поводка 2, а потом поводка 3

Исходные данные:

O 1 O 3 = O 1 O ′ 3 = l 1 - первоначальная длина левого поводка; О 2 О 4 = l 2 -первоначальная длина правого поводка; O 1 O ′′ 3 = l 1 + Δ l 1 - длина левого поводка после перемещения его на величину Δ l 1 ; О 2 О ′ 4 = l 2 + Δ l 2 - длина правого поводка после перемещения его на величину Δ l 2 ; О 1 О 2 = a, О 1 О 4 = О 1 О ′ 4 = b, О 3 О 4 = О ′ 3 О ′ 4 = О ′′ 3 О ′′ 4 = c.

В общем случае:

hhh α = π - arcsin β = arcsin γ = arcsin l1 ,                     l2 ,                    b .

Считаем, что первоначальное положение управляемой платформы определяется горизонтальным положением опорно-поворотного устройства 5 (рис. 2 ‒ 3).

1a) Перемещение правого поводка 2, на величину Δ l 2 :

левый поводок, при этом, не меняет своей длины и поворачивается по дуге окружности, радиусом R 1 = l 1 , а наклонная платформа 4 поворачивается по дуге окружности, радиусом R 2 = b на угол ф 1 .

0 2 0 4² = a ² + b ² - 2 a • b • cos( ^ 1 + / ) , 0 2 0' 4 = I 2 + Л 2 , откуда

^ = arccos

a ² + b ² — ( 1 ₂ + A l ₂) ² _v       2 0 7 b       ,

^—

Y

1 б) Перемещение левого поводка 3, на величину A l 1 :

правый поводок, при этом, не меняет своей длины, остается на месте, а по дуге окружности, радиусом R 3 = c, поворачивается опорно-поворотное устройство 5 на угол ф ₂.

0 1 0*3 = b ² + c ² — 2 b • c • cos( ^ ₂ + y ) , 0 1 0" 3 = 1 1 + Л1 1 , откуда

( b ²

2

= arccos — l

^{+ c 2 — ( l} 1 ^{+ A l} 1⁾²

2 b • c

^—

Y

Теперь поменяем последовательность движений поводков 2 и 3:

2а) Перемещение левого поводка 3, на величину A l 1 :

правый поводок, при этом, не меняет своей длины, остается на месте, а по дуге окружности, радиусом R 3 = c, поворачивается опорно-поворотное устройство 5 на угол ф ₂.

0 1 0* 32 = b ² + c ² — 2 b • c • cos( ф ₂ + y ) , О 1 О" з = l i + Jl i , откуда

Г b2

^, = arccos —

l

+ ^{c 2 — ( l} 1 ^{+ A l} 1⁾²

2 b • c

— Y

2б) Перемещение правого поводка 2, на величину A l 2 :

левый поводок, при этом, не меняет своей длины и поворачивается по дуге окружности, радиусом R 1   = l 1 +Δl 1 , а наклонная платформа 4

поворачивается по дуге окружности, радиусом R₂ = b на угол ф 1 .

0 ₂ 0 4² = a ² + b ² — 2 a • b • cos( ^ 1 + a ) , 0 2 0' 4 = I 2 + Л 2 ,откуда

________________________________ 4 ______________________________

^

= arccos

' a ² + b ² - ( ^/ 2 + ^{Д /} ₂)^{2 2}

(        2 a - b        )

- Y

Сравнивая рис. 2 и рис. 3 видно, что при изменении последовательности поворотов поводков 2 и 3 итоговое положение опорно-поворотного устройства 5 не изменилось.

Итак, задавая перемещения поводков Δl 1 и Δl 2 или углы поворотов φ 1 и φ 2 (как обобщенные координаты), определяем углы поворотов данных поводков. Так как эти поводки связаны с опорно-поворотным устройством 5, на котором расположен рабочий стол, то зная углы поворотов поводков можно определить положение рабочего стола.

Из рис. 2 - 3 видно, что при ф2=ф1 (и ф1=ф2) рис. 2 преобразуется в рис. 4, а рис. 3 в рис. 5. Таким образом, опорно-поворотное устройство 5 опять заняло горизонтальное положение, т.е. произошло поступательное перемещение опорно-поворотного устройства 5. Так как ф2=фь то из выражений (1)–(4) имеем:

arccos

a ²

V

^{+ b 2} - ^{( /} 2 ^{+ Д /} 2 ) 2

2 a - b          ,

^—

Y = arccos

' b l c -nV)

2 b - c

- Y,

откуда a2 + b2 - (l2 + Д/2 )2 b2 + c2 - (/v +Дlv )2

2a -b                   2b -c или

a ² + b ² - ( / ₂ +Д / ₂) ² _a

b ² + c ² - ( / +Д / ) ² c

Рассмотрим частный случай перемещения опорного стола 5, когда φ 2 = φ 1 и φ 1 = φ 2 (рис. 4 ‒ 5). В макете пространственного манипулятора конструктивные параметры подобраны так, что a = c . Тогда из выражения (5) найдем:

k +Дк = /2 +Д/2

________________________________ 5 ____

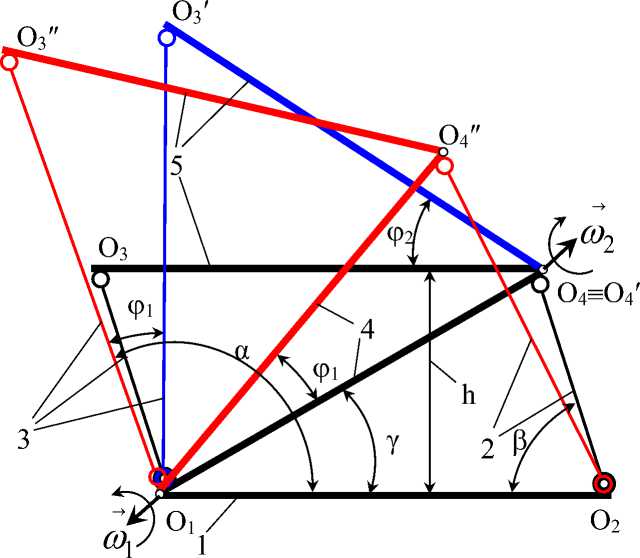
Рис. 3. Схема перемещения фрагмента пространственного механизма при движении поводка 3, а потом поводка 2

Соблюдая условие (6) для манипулятора вида (рис. 1) также можно добиться поступательного перемещения рабочего стола манипулятора. Для нашего макета l 1 = l 2 . Тогда Δl 1 = Δl 2 , т.е. для поступательного перемещения опорно-поворотного устройства данного макета манипулятора необходимо движение поводков 2 и 3 вдоль своей оси на одинаковые величины.

Из [3] известно, что поступательное движение твердого тела получается в 4-х случаях: 1) Поступательных движений твердого тела; 2) Двух вращательных движений твердого тела с равными антипараллельными угловыми скоростями; 3) Винтового движения твердого тела и пары вращений; 4) Двух винтовых движений твердого тела с параллельными осями и равными антипараллельными угловыми скоростями.

________________________________ 6 ____

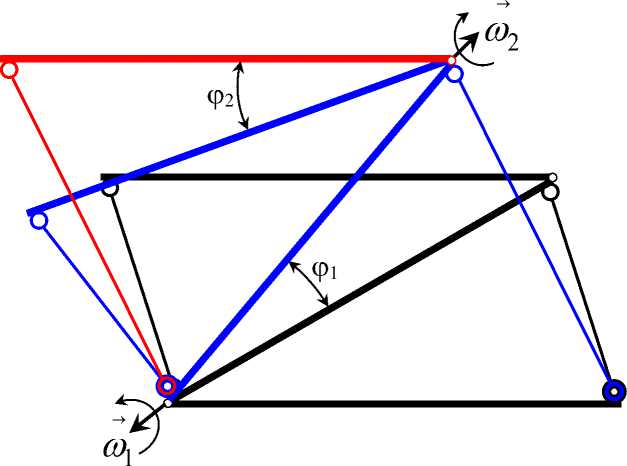
Рис. 4. Схема перемещения фрагмента пространственного механизма при движении поводка 2, а потом поводка 3 при φ 2 = φ 1

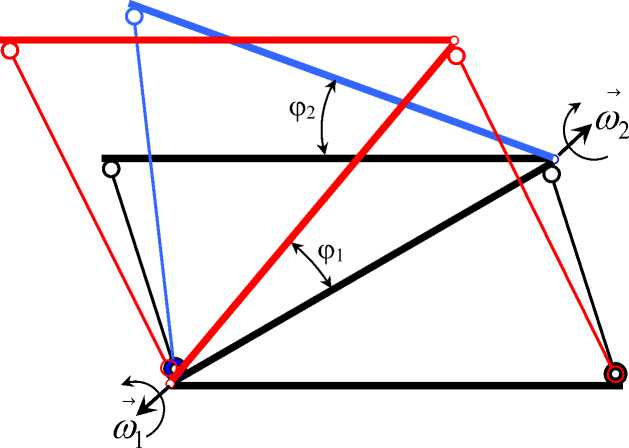
Рис. 5. Схема перемещения фрагмента пространственного механизма при движении поводка 3, а потом поводка 2 при φ 1 = φ 2

В нашем случае - это второй вариант. Отсюда видно, что: ω =- ω , т.е. ••

ϕ ₁ = - ϕ ₂

Вывод:

• 1)    Доказано, что конечные повороты наклонной платформы и опорноповоротного коммутативны в движении, т.е. схемное решение шестикоординатного манипулятора [1] обеспечивает независимость последовательности исполнительных парциальных движений.

• 2)    Соблюдая соотношение (6) можно добиться поступательного вертикального перемещения опорно-поворотного устройства 5 пространственного манипулятора в общем виде.