Конструирование пространственной кривой, составленной из рациональных кубических сегментов

Введение и постановка задачи

Уравнение рационального кубического сегмента имеет вид [1] ^{r (} t ) =

® ₀ r ₀ (1 - t )³ + 3 ® ₁ r Q t (1 - t )² + 3 ® ₂ r P t ² (1 - t ) + ® з Г 1 1 ³   , (1)

O o (1 — t ) + 3 ® 1 t (1 — t )   + 3 ® 2 1 (1 — t ) I 0) 3 1

где параметр t изменяется в диапазоне [0, 1], а весовые коэффициенты ω₀, …, ω₃ могут принимать любые положительные значения. Векторы r 0 , r Q , r P , r 1 указывают узловые точки R 0 , Q , P , R 1 характеристической ломаной (рис. 1). При равенстве весовых коэффициентов кривая (1) вырождается в кубическую кривую Безье [2].

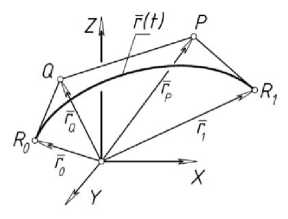
Рис. 1. Кубический сегмент

В статье рассматриваются две задачи.

Задача 1 . Через указанные в пространстве точки R ₀, R ₁, R ₂, … с заданными в этих точках направляющими τ₀, τ₁, τ₂, … требуется провести G2-гладкую составную кривую, касающуюся заданных направляющих (рис. 2). Гладкость G2 означает непрерывное изменение вектора кривизны вдоль кривой, без «скачков» по модулю и направлению [3, 4]. Направляющие прямые могут рассматриваться как элемент управления формой конструируемой кривой.

Задача 2 . В пространстве даны не связанные между собой кубические кривые R ₀– R ₁ и R ₂– R ₃ (рис. 3). Требуется найти кубический сегмент R ₁– R ₂, соединяющий заданные кривые («вставка сегмента»).

В научной литературе встречаются формулировки задач 1, 2, но конструктивные пошаговые алгоритмы их решения отсутствуют. Так, например, в работе [5, с. 153] исследуются условия G2-гладкого соединения кубических сегментов Безье, но результат представлен в аналитической форме, затрудняющей их практическую реализацию. Кроме того, на пояснительном чертеже [5, рис. 6.8] ошибочно показаны сегменты, в точке соединения которых вектор кривизны скачком меняет свое направление, то есть не обеспечивается условие G2-гладкости. В работе [6, с. 108] авторы ограничиваются констатацией очевидного факта, что соприкасающиеся плоскости кубических сегментов в точке их соединения должны совпадать.

Задача вставки сегмента упоминается в работе [5, с. 155], где предложено обеспечивать заданную кривизну на концах вставляемого сегмента посредством «подбора» весовых коэффициентов ω0, …, ω3, но алгоритм подбора не рассматривается.

Для решения поставленных задач авторами разработаны конструктивные пошаговые графоаналитические алгоритмы. Отличительная особенность предлагаемых алгоритмов заключается в существенном использовании средств и методов трехмерной компьютерной графики.

Рациональный кубический сегмент(общие сведения)

Векторы кривизны K (0) и K (1) в начальной R ₀( t = 0) и конечной R ₁( t = 1) точках рационально-

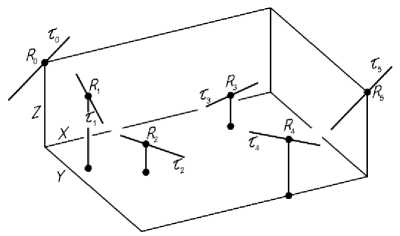
Рис. 2. Условие задачи 1

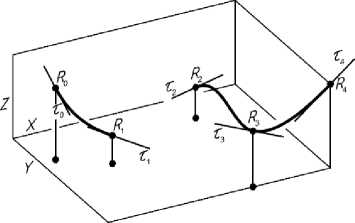
Рис. 3. Условие задачи 2

го кубического сегмента определяются по формулам

K (0) =

r (0) X r(0)

I r (0)|^{3    ,}

K (1) =

r (1) х Г (1)

I r (1)|^{3   ,}

где

^{r (0)} = 3— ⁽ r _e - ^r 0 ),   r (!) = ³ ^(г - r P )

^0

r(0) = (6W + 6W -18^)(re - r0) + 6^(rP - re), (3) w0   W0    ®0

WWWw

r(1) = (6— + 6— -184)(rp - ri) + 6—(re - rp )• w3   w3    W2

Выражения (3) получены в результате дифференцирования функции (1) по параметру t [5, с. 155]. Подставляя (3) в (2), после ряда алгебраических преобразований получаем:

• 2    W 0 W 2 R 0 Q X QP .

■K⁽⁰⁾   ^o        i ;

• ³    w 2    1 R 0 Q I³

• 2    WW QP X PR 1

• ³   w 2     | PR 1 I³  ’

Здесь R 0 Q , QP , PR 1 – векторы, соединяющие узловые точки характеристической ломаной сегмента (1). Если узловые точки отмечены на компьютерном 3D-макете, то векторные произведения, входящие в (4), могут быть определены графически. Например, для расчета модуля векторного произведения R ₀ Q x QP достаточно построить (непосредственно на 3D-макете) параллелограмм со сторонами R 0 Q и QP , после чего определить (с помощью блока справочной информации используемого графического пакета) площадь этого параллелограмма [7].

Если зафиксирована характеристическая ломаная кубического сегмента (см. рис. 1) и задан вектор кривизны K (0) в его начальной точке R ₀, то из (4) следует

Решение задачи 1

(графоаналитический алгоритм)

Требуется сформировать кривую, проходящую через наперед заданные точки R 0 , R 1 , R 2 , … и касающуюся в этих точках наперед заданных прямых τ 0 , τ 1 , τ 2 , … (см. рис. 2). Предлагается решать задачу последовательно: к первому сегменту R ₀– R ₁ добавляем второй сегмент R ₁– R ₂, обеспечивая в стыковой точке R ₁ общую касательную и общий вектор кривизны соединяемых сегментов [8, 9]. К найденному сегменту R ₁– R ₂ добавляем следующий сегмент R 2 – R 3 , также добиваясь совпадения касательных и векторов кривизны в стыковой точке R 2 , и так далее.

Таким образом, решение задачи 1 сводится к многократному решению одной и той же задачи: построению кубического сегмента r i ( t ), проходящего через заданные граничные точки R_{i -1}, R_i , касающегося в заданных точках направляющих прямых τ _{i -1}, τ _i и имеющего в начальной точке наперед заданный вектор кривизны K _{i -1}. Уравнение искомого сегмента будем искать в форме (1).

На начальный (первый) сегмент R ₀– R ₁ накладываются слабые требования: инцидентность заданным точкам R 0 , R 1 и соприкосновение с направляющими прямыми τ 0 , τ 1 . Для выполнения этих требований достаточно разместить управляющие точки Q 1 , P 1 характеристической ломаной R 0 Q 1 P 1 R 1 конструируемого сегмента на заданных касательных τ₀, τ₁ (рис. 4). Весовые коэффициенты ω₀, …, ω₃ первого сегмента могут быть назначены произвольно, по усмотрению конструктора.

w^=Wi^ RQL w 2   2¹  ^'| R „ Q x QP |

.

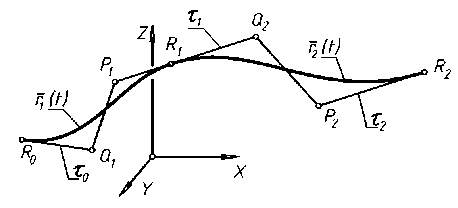
Рис. 4. Соединение сегментов

При выполнении условия (5) и при любом значении ω₃ будет получена заданная кривизна K (0) в начале сегмента. Произвольно изменяя значения весовых коэффициентов ω₀, ω₁, ω₂, ω₃, но сохраняя расчетное значение (5), получаем множество рациональных кубических кривых (1) с одной и той же кривизной в начальной точке сегмента.

Если задан вектор кривизны K (1) в конечной точке R 1 сегмента (1), то из (4) следует:

Задав характеристическую ломаную и весовые коэффициенты, определяем, согласно (4), вектор кривизны в конечной точке R 1 первого сегмента:

К «(l) = 2 WW Q 1 P x P 1 R 1

³ w 2      | P 1 R 1 |^{3    ,}

m. = V(1)|^ PR 1L w 2     2^{1 V3I}| QP x PR 1|

где надстрочный индекс в скобках означает номер сегмента. Модуль входящего в (7) векторного произведения Q 1 P 1 X P 1 R 1 находим графически, построив параллелограмм на отрезках Q 1 P 1 , P 1 R 1 и

При выполнении условия (6) и при любом значении ω 0 сохраняется заданная кривизна K (1)

в конце сегмента.

определив его площадь с помощью справочных средств используемого графического пакета. Модуль вектора P 1 R 1 также определяем графически. Подставляя найденные значения в (7), вычисляем модуль | K ⁽¹⁾(1)| вектора кривизны в конечной точ-

ке первого сегмента. Этот вектор направлен перпендикулярно соприкасающейся плоскости Е₁( Q i P i R i ), причем векторы Q i P i , P i R i , K ⁽¹⁾(1) образуют правую тройку.

Таким образом, сформирован первый (начальный) сегмент r _i( t ) искомой составной кривой, а также найден вектор кривизны K ⁽¹⁾(1) в его конечной точке. Визуализация сегмента выполняется средствами трехмерной компьютерной графики [i0, ii]. Для этого достаточно разложить векторную функцию (1) по осям координат x , y , z и запрограммировать построение графика параметрически заданной функции x ( t ), y ( t ), z ( t ) при изменении параметра t в диапазоне [0, 1].

Сформировав первый сегмент и определив вектор кривизны в его конечной точке, присоединяем к нему следующий (второй) сегмент в соответствии с изложенным ниже алгоритмом.

Шаг 1 (построение характеристической ломаной второго сегмента). Управляющие точки Q ₂, P ₂ характеристической ломаной R _i Q ₂ P ₂ R ₂ второго сегмента r ₂( t ) должны быть инцидентны наперед заданным касательным т₁, т₂ (см. рис. 4), но для О2-гладкого соединения второго сегмента с ранее рассчитанным первым сегментом этого недостаточно. Необходимо обеспечить совпадение соприкасающихся плоскостей Е₁⁽¹⁾ и Е₁⁽²⁾ соединяемых сегментов в стыковой точке R _i. Соприкасающаяся плоскость первого сегмента Е₁⁽¹⁾( Q _i P _i R _i) в точке R _i определена самой точкой R _i и положением зафиксированных ранее управляющих точек Q _i, P _i. Положение соприкасающейся плоскости второго сегмента Е₁⁽²⁾( R _i Q ₂ P ₂) определяется точками R _i, Q ₂, P ₂. Чтобы соприкасающиеся плоскости совпали, требуется поместить управляющие точки Q 2 , P ₂ второго сегмента в плоскость Е/^ Q _i P _i R _i). Управляющая точка Q ₂ на касательной т₁ может быть указана произвольно, так как эта касательная лежит в соприкасающейся плоскости. В отличие от точки Q 2 , точка P 2 не может быть произвольно указана на касательной т₂, так как она должна находиться одновременно как на т₂, так и в соприкасающейся плоскости. Поэтому точку P ₂ следует отметить на пересечении прямой т₂ и соприкасающейся плоскости Е₁⁽¹⁾: P 2 = Т 2 П Е ⁽¹⁾. Эта типовая задача начертательной геометрии (построение точки пересечения прямой и плоскости) решается непосредственно на 3Э-макете средствами компьютерной графики.

Результат шага 1 : найдена характеристическая ломаная второго сегмента r ₂( t ), исходя из условия совпадения соприкасающихся плоскостей Е₁⁽¹⁾ и E_i⁽²⁾ соединяемых сегментов в стыковой точке R _i (см. рис. 4). Выполнение этого условия гарантирует коллинеарность векторов кривизны соединяемых сегментов r i ( t ) и r 2 ( t ) в точке стыка, но не обеспечивает ни равнонаправленности, ни совпадения модулей этих векторов.

Шаг 2 (расчет комплекса весовых коэффициентов второго сегмента). Комплекс весовых коэффициентов второго сегмента вычисляется в соответствии с (5):

= З^^ИТ^ОАл, ω ₁     2          | R₁Q₂ × Q₂P₂ |

где модуль вектора кривизны |K(2)(0)| в начальной точке сегмента известен (равен модулю вектора кривизны |K(i)(1)| в конечной точке предыдущего сегмента). Как и на шаге 1, модуль входящего в (8) векторного произведения R1Q2 х Q2P2 находим графически, построив параллелограмм на отрезках R1Q 2, Q2P 2 и определив его площадь с помощью справочных средств используемого графического пакета. Модуль вектора RiQ2 также определяем графически. При выполнении условия (8) и при любом значении ю3 получаем заданную кривизну в начале сегмента.

Для обеспечения равнонаправленности векторов кривизны в стыковой точке необходимо потребовать, чтобы управляющие точки Qi, P2 соединяемых сегментов, лежащие в соприкасающейся плоскости Е1(1) = Е1(2), располагались по одну сторону от касательной т1 (см. рис. 4). Если указанное требование не выполнено, задача не имеет решения. В этом случае следует таким образом изменить положение направляющей прямой т2, чтобы точка P = Т2 П Е(1) оказалась по ту же сто рону от касательной т1, что и точка Q1.

Результат шага 2 : найден комплекс (8) весовых коэффициентов второго сегмента. Произвольно изменяя значения весовых коэффициентов ю₀, ю₁, ю₂, ю з , но сохраняя расчетное значение (8), получаем множество рациональных кубических кривых вида (1) с наперед заданным модулем кривизны в начальной точке. Дополнительная возможность управления формой сегмента обусловлена вариативностью положения управляющей точки Q ₂.

Шаг 3 (расчет вектора кривизны в конечной точке второго сегмента). Для присоединения ко второму сегменту следующего (третьего) сегмента надо рассчитать вектор кривизны K ⁽²⁾(1) в конце второго сегмента. Этот вектор рассчитывается в соответствии с формулой (4):

(2)      2 ω 1 ω 3 Q 2 P 2 × P 2 R 2

3 ω ²₂    | P ₂ R ₂ |³

.

Вектор K(2)(1) перпендикулярен плоскости Е2(2)( Q 2 P2 R 2), соприкасающейся со вторым сегментом в его конечной точке R2. Как и на предыдущих шагах алгоритма, модуль входящего в (9) векторного произведения Q2P2 × P2R2 находим графиче- ски, построив параллелограмм на отрезках Q2P2, P2R2 и определив его площадь с помощью справочных средств используемого графического пакета. Модуль вектора P2R2 также определяем графи- чески.

Результат шага 3 : определен вектор кривизны в конечной точке второго сегмента. Этот вектор необходим для G2-гладкого подключения ко второму сегменту следующего (третьего) сегмента.

Многократно повторяя шаги 1…3 рассмотренного алгоритма, получаем полное решение задачи 1 (построение G2-гладкой составной кривой, проходящей через заданный набор точек и касающейся в этих точках заданных направляющих прямых).

Пример 1

Требуется соединить (с гладкостью G2) кубические сегменты r i ( t ) и r ₂( t ). Кубический сегмент r i ( t ) зафиксирован. Он задан граничными точками R ₀(20; 35; 10), R 1 (50; 35; 20) и управляющими точками Q 1 (30; 25; -5), P 1 (33; 47; 21). Все весовые коэффициенты первого сегмента приняты равными единице.

Второй кубический сегмент задан граничными точками R 1 , R ₂(80; 0; 30), а также общей для соединяемых сегментов касательной т₁. В конечной точке R ₂ второго сегмента задана вертикальная касательная т₂ (рис. 5). Управляющие точки Q ₂, P ₂ и весовые коэффициенты второго сегмента неизвестны. Их следует определить из условия G2-гладкого соединения сегментов r ₁( t ) и r ₂( t ).

Решение . Найдем уравнение и выполним визуализацию первого сегмента r ₁( t ). Подставляем координаты узловых точек и значения весовых коэффициентов этого сегмента в векторную функцию (1) и раскладываем ее по осям координат. Учитывая, что (1 - 1 )³ + 3 t (1 - 1 )² + 3 1 ²(1 - 1 ) + 1 ³ = 1 при любом значении параметра t в диапазоне [0, 1], получаем параметрически заданную скалярную функцию:

x ( t ) = 20(1 - 1 )³ + 90 1 (1 - 1 )² + 99 1 ² (1 - 1 ) + 50 1 ³;

y 1 ( t ) = 35(1 - 1 )³ + 75 t (1 - 1 )² + 141 1 ²(1 - 1 ) + 35 t ³; (10) _z 1 ( t ) = 10(1 - 1 )³ - 15 t (1 - 1 )² + 63 1 ²(1 - 1 ) + 20 1 ³.

Уравнения (10) позволяют выполнить визуализацию сегмента r ₁( t ) в любой компьютерной программе, дающей возможность пользователю программировать построение графика аналитически заданной функции.

Учитывая, что весовые коэффициенты сегмента r1(t) приняты равными единице, получаем, согласно (4), вектор кривизны этого сегмента в конечной точке R1:

K_W   = 2 ^Q ₁ P ₁ х PR .       (11)

3   | P 1 R 1 |³

Модуль входящего в (11) векторного произ- ведения равен площади параллелограмма, построенного на отрезках Q1P1, P1R1. Эта площадь и длина отрезка P1R1 определены с помощью справочных средств компьютерной графики: S1 = 670,9881; P1R1 = 20,8327 (см. рис. 5). Подставляя найденные величины в (11), получаем: |K(1)(1)| = 0,049475.

Проверка . Это же значение модуля кривизны в конечной точке сегмента r ₁( t ) получается, если использовать известную [3] формулу

I K | 2 =

( z y - y z )² + ( x z - zx )² + ( yx - xy )

, (12)

( x ² + y ² + Z ²)³

где значения входящих в (12) производных определяются дифференцированием функции (10) с последующей подстановкой t = 1.

Найдем управляющие точки Q ₂, P ₂ характеристической ломаной второго сегмента r ₂( t ). Точка Q ₂ может быть произвольно размещена на касательной т₁, например, на расстоянии R ₁ Q ₂ = 20. Точку P ₂ находим на пересечении вертикальной касательной т₂ с плоскостью E₁⁽¹⁾( Q ₁ P ₁ R ₁) (см. шаг 1 алгоритма). С помощью справочных средств компьютерной графики определяем координаты точек Q 2 (66,2601; 23,3853; 19,1588) и P 2 (80; 0; 3,2317).

По формуле (8) рассчитываем комплекс весовых коэффициентов второго сегмента:

^2 = ³ I K ⁽²⁾ (0) I     R ¹ Q

® 2    2     ^‘ir^ х Q 2 P 2 I

.

Здесь | K ⁽²⁾(0)| = | K ⁽¹⁾(1)| = 0,049475, R 1 Q ₂ = 20, а модуль векторного произведения равен площади S₂ = 370,4553 параллелограмма, построенного на сторонах R ₁ Q ₂, Q ₂ P ₂ (см. рис. 5).

Подставляя указанные значения в (13), полу- ю ю чаем:   0 2 = 1,6026. Отдельные значения весо- ю2

вых коэффициентов могут варьироваться. Положим, например, ю0 = 1,6026, ю1 = ю2 = 1. Значение весового коэффициента ю3 не влияет на кривизну в

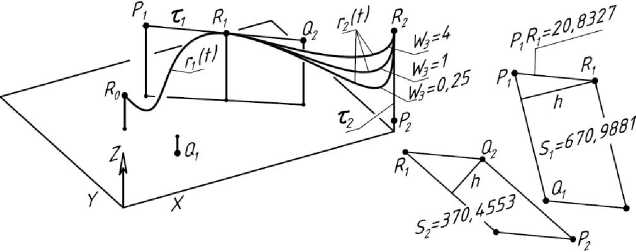
Рис. 5. К примеру 1

начальной точке сегмента, поэтому ω 3 может задаваться произвольно. При изменении ω 3 изменяется форма конструируемого сегмента r 2 ( t ).

Для визуализации сегмента r 2 ( t ) подставляем координаты узловых точек и значения весовых коэффициентов этого сегмента в векторную функцию (1) и раскладываем ее по осям координат x , y , z . Получаем параметризованное уравнение сегмента: x ₂ ( t ) = — [80,13(1 - 1 )³ + 198,7803 1 (1 - 1 )² +

Ф ⁽ t )

+ 240 1 ²(1 - 1 ) + 80 ® ₃ 1 ³];

y ₂ ( t ) = —[56,091(1 - 1 )³ + 70,1559 1 (1 - 1 )²];   (14)

• ²       ф ( t )

z ₂ ( t ) = — [32,052(1 - 1 )³ + 57,4764 1 (1 - 1 )² +

Ф ⁽ t )

+9,695112(1 -1) + 30®313], где ф(t) = 1,6026(1 -1)3 + 3t(1 -1)2 + 312 (1 -1) + ю313. Параметр t меняется в диапазоне [0, 1]. Уравнения (14) позволяют выполнить визуализацию сегмента r2(t). Присваивая весовому коэффициенту ω3 различные значения, получаем сегменты r2(t) различной формы, но с неизменной кривизной в начальной точке (см. рис. 5).

Решение задачи 2

(графоаналитический алгоритм)

Не связанные между собой рациональные кубические сегменты r ₁( t ) и r ₃( t ) вида (1) зафиксированы своими характеристическими ломаными и весовыми коэффициентами (рис. 6). Требуется найти кубический сегмент r ₂( t ), гладко (с гладкостью G2) соединяющий заданные сегменты.

Согласно (4), графоаналитически определяем вектор кривизны K ⁽¹⁾(1) в конечной точке R 1 первого сегмента r 1 ( t ). Аналогично определяем вектор кривизны K ⁽³⁾(0) в начальной точке R 2 третьего сегмента r 3 ( t ). Вставляемый сегмент r 2 ( t ) должен иметь точно такие же векторы кривизны в своих граничных точках R 1 и R 2 .

Шаг 1 (построение характеристической ломаной). Управляющие точки Q ₂, P ₂ характеристической ломаной R ₁ Q ₂ P ₂ R ₂ вставляемого сегмента r ₂( t ) должны быть инцидентны касательным τ₁, τ₂. Для G2-гладкого соединения этого недостаточно. Необходимо обеспечить совпадение соприкасающихся плоскостей соединяемых сегментов в точках стыка R 1 , R 2 . В точке R 1 соприкасающаяся плоскость Σ 1 ⁽¹⁾ первого сегмента определена точками R 1 , Q 1 , P 1 . Соприкасающаяся плоскость Σ 1 ⁽²⁾ вставляемого сегмента определена точками R 1 , Q 2 , P ₂. Эти плоскости должны совпадать:

SP( R 1 Q 1 P ) =E < ²⁾( R 1 Q ₂ P ₂).       (15)

В точке R ₂ получаем аналогичное условие:

s 2 ²⁾( R 2 q ₂ P 2 ) = e 2 ³⁾ ( R 2 Q 3 P 3 ).      (16)

Здесь надстрочный индекс (в скобках) обозначает номер сегмента, а подстрочный индекс – номер узловой точки R_i .

Таким образом, искомые управляющие точки Q2, P2 вставляемого сегмента должны находиться на касательных τ1, τ2 и удовлетворять условиям (15), (16). Этот комплекс требований выполняется, если точки Q2, P2 находятся на пересечении каса- тельных с соприкасающимися плоскостями:

Q 2 = T 1 П ^ ³⁾( R 2 Q 3 P 3 ), P 2 = ' П ^^Ц( RQ 1 P 1 ).  (17)

Для обеспечения равнонаправленности векторов кривизны в стыковой точке R1 требуется, чтобы управляющие точки Q1, P2 сегментов r1(t) и r2(t), лежащие в соприкасающейся плоскости Σ1(1) = Σ1(2), располагались по одну сторону от касательной τ1. Аналогичным образом для обеспечения равнонаправленности векторов кривизны в стыковой точке R2 требуется, чтобы управляющие точки Q2, P3 сегментов r2(t) и r3(t), лежащие в соприкасающейся плоскости Σ2(2) = Σ2(3), располагались по одну сторону от касательной τ2.

Если указанные требования не выполнены, задача не имеет решения.

Шаг 2 (расчет весовых коэффициентов вставляемого сегмента). Согласно (8), в начальной точке вставляемого сегмента r2(t) должно выполнять- ся условие

= I'K^nFRQJrFi,  <'8’ й|    2          I R1Q2 x Q2P2 I где модуль вектора кривизны |K(2)(0)| известен (равен модулю вектора кривизны |K(1)(1)| в конеч- ной точке первого сегмента). Модуль входящего в

(18) векторного произведения R1Q2 x Q2P2 нахо- дим графически, построив параллелограмм на отрезках R1Q2, Q2P2 и определив его площадь с помощью справочных средств используемого графического пакета. Модуль вектора R1Q2 также определяем графически.

Согласно (9), в конечной точке вставляемого сегмента должно выполняться условие

= 3| K (2) (1)|     ^{| P} 2 R 2 ^|3    ,

® 2     2^{1       2} । Q 2 P 2 x P 2 R 2 I

где модуль вектора кривизны | K ⁽²⁾(1)| равен модулю вектора кривизны | K ⁽³⁾(0)| в начальной точке третьего сегмента. Как и ранее, модули векторов и векторных произведений, входящих в (19), определяем графически.

При выполнении условий (18), (19) получаем искомый сегмент r ₂( t ), гладко соединяющий сегменты r ₁( t ) и r ₃( t ).

Примечание. При произвольном изменении значений отдельных весовых коэффициентов, входящих в (18), (19), форма вставляемого сегмента не меняется, то есть задача G2-гладкой вставки рационального кубического сегмента (1) имеет единственное решение.

Пример 2

Даны кубические сегменты   r 1 ( t )  и   r 3 ( t )

(рис. 7а). Требуется найти кубический сегмент

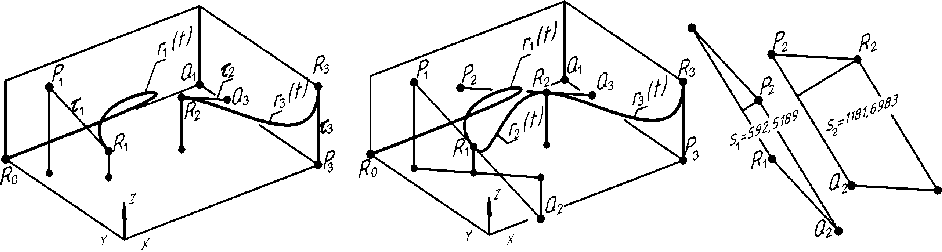
а)                                                                  б)

Рис. 7. К примеру 2

r 2 ( t ), гладко (с гладкостью G2) соединяющий заданные сегменты.

Рациональный кубический сегмент r 1 ( t ) задан характеристической ломаной R 0 (0; 65; 0)– Q 1 (80; 65; 0)– P 1 (6; 49; 33)– R 1 (20; 35; 10) и весовыми коэффициентами ω 0 = 2; ω 1 = 6; ω 2 = 1,5; ω 3 = 0,75. Модуль кривизны сегмента в конечной точке равен | K ⁽¹⁾(1)| = 0,09316.

Сегмент r ₃( t ) задан как кубическая кривая Безье (все весовые коэффициенты равны единице) с характеристической ломаной R ₂(50; 35; 20)– Q ₃(62; 26; 19)– P ₃(80; 0; 0)– R ₃(80; 0; 30). Модуль кривизны сегмента в его начальной точке равен | K ⁽³⁾(0)| = 0,05808.

Решение

Согласно (17), находим управляющие точки Q 2 (35,7087; 19,2913; –15,8071), P 2 (27,3414; 51,9939; 21,8882) характеристической ломаной искомого сегмента r ₂( t ). Чтобы рассчитать комплексы весовых коэффициентов (18), (19), определяем (с помощью справочных средств компьютерной графики) модули входящих в эти выражения векторов: R ₁ Q ₂ = 34,0519; P ₂ R ₂ = 28,3861; S 1 = I R 1 Q 2 * Q ₂ P ₂ I = 592,5189; S 2 = | Q ₂ P ₂ * P ₂ R ₂ | = 1181,6983. Подставляя найденные значения в (18), (19), получаем:

^2 = 9,3123; ^M l = 1,6864. (20) M f ® 2

Произвольно назначаем ω₁ = ω₂ = 1. Согласно условиям (20), получаем ω 0 = 9,3123; ω 3 = 1,6864.

Подставляем координаты точек R 1 , Q 2 , P 2 , R 2 и значения весовых коэффициентов в векторное уравнение (1). Раскладывая (1) по осям координат, получаем скалярные уравнения искомого сегмента r 2 ( t ):

x ( t ) = J- [186,246(1 - 1 )³ + 107,1261 t (1 - 1 )² +

• ²       Ф ₂ ( t )

+ 82,0242 1 ²(1 - 1 ) + 84,32 1 ³];

y ₂ ( t ) =   ¹   |325,9305(l - 1 )³ + 57,8739 1 (1 - 1 )² +

Ф ₂ ( t )

+ 155,9817 1 ²(1 - 1 ) + 59,024 1 ³];

z ₂ ( t ) =        [93,123(1 - 1 )³ - 47,4213 t (1 - 1 )² +

• ²       Ф 2 ( t )

+65,664612(1 -1) + 33,72813], где

Ф ₂ ( t ) = 9,3123(1 - t )³ + 3 t (1 - t )² + 3 t ² (1 - t ) + 1,6864 t ³. Параметр t меняется в диапазоне [0, 1]. Визуализация сегмента r 2 ( t ) представлена на рис. 7б.

Заключение

Предложен графоаналитический алгоритм, позволяющий формировать составную G2-гладкую кривую, проходящую через наперед заданные в трехмерном пространстве точки и касающуюся в этих точках наперед заданных прямых.

Предложен графоаналитический алгоритм вставки кубического сегмента, гладко (с гладкостью G2) соединяющего наперед заданные кубические кривые.

Отличительная особенность предложенных алгоритмов состоит в существенном использовании справочных средств трехмерной компьютерной графики.

Представленные в статье примеры решения задач 1 и 2 транспарентны и могут быть использованы в учебном процессе.