Контактная задача упругого кольца и жесткого основания

V.N. TARASBV, N.B. SMBLEVA

CONTACT PHHBLEM HF ELASTIC RIHG АНН RIGID BASE

Institute of Physics and Mathematics, Federal Research Centre Komi Science Centre, Ural Branch, RAS, Syktyvkar

Решению контактных задач для гибких элементов конструкции в настоящее время уделяется большое внимание. Это вызвано, с одной стороны, необходимостью расчета все более сложных конструкций, а с другой, - с развитием современных методов решения задач, возникающих в теории стержней, пластин и оболочек с неизвестной областью активного взаимодействия элементов конструкции, развитием численных методов, теории оптимизации и вариационного исчисления. В настоящей работе рассматривается контактная задача кругового кольца, испытывающего весовую нагрузку и находящегося над жестким основанием. Определяются граница области активного взаимодействия (область контакта) и силы реакции связи, что может оказаться полезным для расчета износостойкости колец.

Некоторые контактные задачи, в том числе и задачи устойчивости упругих систем при наличии односторонних ограничений на перемещения, и методы их решений рассмотрены в работе [1-3].

Представим, что тонкий упругий стержень находится под действием сил и нагрузки, распределенной по его оси. Введем в точке М на оси стержня систему координат @,у,г\ ось г направлена по касательной к оси стержня, оси ж и у - по главным осям инерции поперечного сечения, ds - элемент длины стержня, s -длина, отсчитываемая от некоторой точки Mq. Пусть точка М движется со скоростью, равной 1 (^ = 1), тогда система координат @,у, г) будет вращаться с некоторой угловой скоростью Q, проекции которой на оси (ж, у, г) обозначим через VpafY

В точке М приложены силы (14, Vy, V?) и моменты (М^Му, M,Y а также вектор внешней нагрузки ^F^, Fy, F_KY Тогда уравнения равновесия Кирхго-

фа [4] имеют вид

Г^-гЦ + 9Ц + < = 0,

<^-_РУ₂ + гУ_г+Р_у = о, (1) к^-дУ_ж+рУ_у + г_г=о.

( "11 ^{— т}^у 4 94 ^— 4 = О, №-_PL₃+rL_g4X = 0,     (2)

№ -qb«y pL_y = 0.

В недеформированном (первоначальном) состоянии оси х, -у, z обозначим через хо, уо, zq. Соответствующую угловую скорость - через Qq с проекциями (ро, до, го) ^{на оси} (^о, ^/о, ^о) соответственно.

В результате деформации стержня точка М получает перемещение, проекции которого на оси (жо, З/о, ^о) обозначим через (u, v, w). Векторы (р, q, г) и (ро, до, го) характеризуют изменения кривизны стержня в результате деформации.

Считая деформации малыми, можно записать уравнение Клебша [4]:

р = ро + ^, g = до + й_? г = го + 5т^

5Р= 11 -тоР + 907,

8q = ^ - Pol + г_оа,          (3)

Sr = Ц - qoa УроР, где (а, /3, 7) - косинусы углов между осями (ж, у, z) и (^о, Уо, ^о)-

	X	У	Z
ж0	1	—а
Уо	а	1	—а
20	-р	а	1

Углы а, (3, ^ связаны с перемещением уравнениями:

Р = ^ + gow - rov, -а= ^-Vrou-pow.        (5)

0 = ^+pov-9o«.

Считаем, что ось стержня в недеформированном состоянии представляет собой окружность радиуса R. Тогда ро = 0, qo = -^, го = 0, и предположим, что кольцо нагружено весовой нагрузкой:

F_y = 0, ds = Rdd^

d - центральный угол, отсчитываемый от оси £, (£, О - некоторая неподвижная система координат (рис. 1), так что координаты точки М кольца в недеформированном состоянии определяются формулами:

^ = ^cos^, £ = Д sin 19.

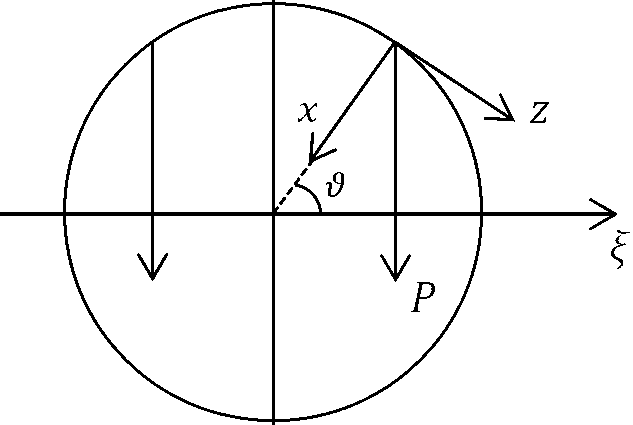
Рис. 1. Кольцо с весовой нагрузкой.

Fig. 1. Weighted ring.

В нашем случае деформация кольца плоская, таким образом, уравнения Кирх го фа-Клебша упрощаются.

Уравнения равновесия будут иметь вид:

Гт^+94^ = й

<    - qV_$ ух* = о,

V ds р = 0, д = до + 5q^ г = 0,

Sq = ^, Ly=B6q, q0 = -(p=^ + qow, \0 = ^-q№

ds = RdO, 5q = ds

где В - жесткость стержня при изгибе.

Координаты точек деформированного кольца определяются уравнениями

(^ = (R — и) cos в — w sin 0, [ £ = (R — ц) sin 9 + w cos 9.

Пусть кольцо находится под жестким препятствием так, что

( = (R — и) sin 9 + w cos 9 > — R. (10)

Наличие неравенства (10) приведет к тому, что силы Р_ж и F_z становятся неизвестными и подлежат определению. Поэтому перейдем к вариационной постановке задачи.

Известно [5,6], что упругая энергия стержня в квадратичном приближении определяется изменением кривизны (замечая, что ds = Rd9)

v-^L 5qd9^^j0 (u +иМ и второе уравнение в (7) принимает вид (условие несжимаемости оси стержня):

u = wz.                  (11)

Предположим, что по ободу кольца равномерно распределена весовая нагрузка Р, направленная как это показано на рис. 1. Проектируя эту силу на оси ^а), получим: Р,. ■= Psin9,P_z = Pcos9. Считая деформации малыми, работу вешних сил можно определить формулой

/*2тг                       /*2тг

А = Р ^(9)d9 = Р / (—usin# + w cos 9)d9.

Jo              Jo

Таким образом, получаем задачу вариационного исчисления или (ад, с) = 0.

Таким образом, получаем задачу выпуклого квадратичного программирования

У — 2тгРР.у„ м ^ min         (19)

при ограничениях (17), (18). Без ограничения общности можно считать ^ = 1. Результаты вычислений представлены на рис. 2-5.

V — А —> min             (12)

при выполнении ограничений (10) и условия несжимаемости (11).

Для конечномерной аппроксимации представим го в виде частичной суммы ряда Фурье:

го = 52 уь sin к9 + y/,-^ cos к9, 9 G [0, 2тг]. (13) к=1

Тогда из условия несжимаемости и = 52 у^к cos к9 — уь+пкsin к9.    (14)

к=1

Подставляя (13) и (14) в выражения для упругой энергии и работы внешних сил, учитывая условие ортогональности тригонометрических функций, получим р п

^ = 5дз 52 ^С^ ” ^ + 52 ^PnoV - I)2, 3=03=1

А = 27гРРута+1.(16)

Потребуем, чтобы ограничения (10) выполнялись в конечном числе точек ^ :

/3      7г\    777, ,

Тогда неравенства (10) запишем в виде:

52 уэа» + 52 dj^aj^ + bj < 0,(17)

3=13=1

где а, = з cos(j^) sin(^) - sin(j^) cos^), аэ*п = -SsN-MNHPj) - cos(j^)cos(yy), bj = -^(1 +sin(^)).

Необходимо исключить перемещение кольца как жесткого целого в направлении оси (. Для этого потребуем,чтобы

<(°Ж(|) +^(тг) + ^у) =0:

что приводит при п = 10 к равенству:

4^1 + 4^з + 8^5 + 827 + 20^д + 20гц + 28ci3 +

4-28^15 + 36^17 + 36ci9 = 0 (18)

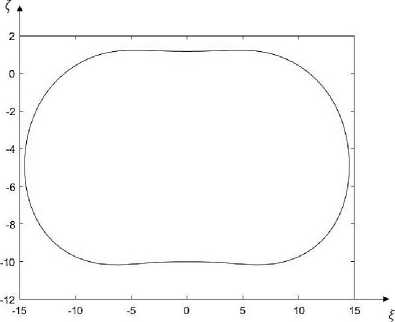
Рис. 2. Форма равновесия кольца при Р = 20.

Fig. 2. Ring equilibrium form at P = 20.

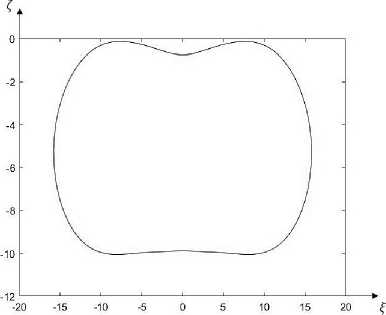
Рис. 3. Форма равновесия кольца при Р = 30.

Fig. 3. Ring equilibrium form at P = 30.

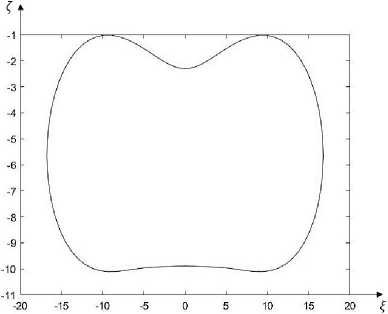
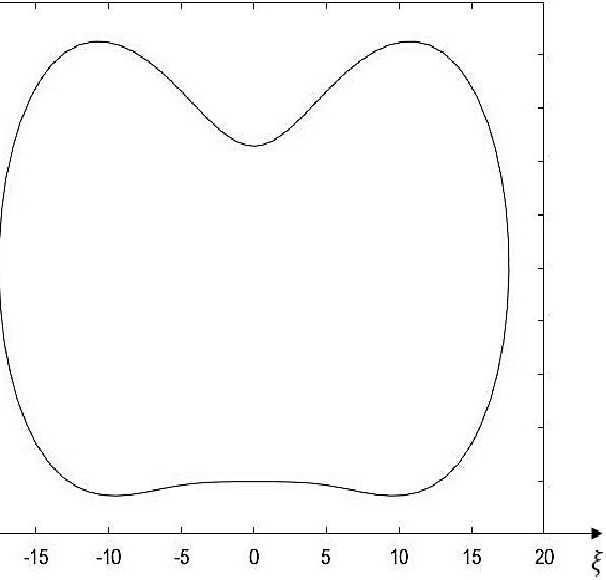
Рис. 4. Форма равновесия кольца при Р = 40.

Fig. 4. Ring equilibrium form at P = 40.

<

-1 -

-2 -

-3 ■

-4 -

-5 ■

-6 -

-7 -

-8 -

-9 -

■10 -

■11

-20

имеет вид:

у = у (А) = -(Q^g + Q~A^tA).

Введем в рассмотрение функцию

^(А) = min (А, у). уЕН^2тг

Тогда и поиск седловой функции Лагранжа сводится к задаче квадратичного программирования

ф(ХД = тах<^(А). АеА

Рис. 5. Форма равновесия кольца при Р = 50.

Fig. 5. Ring equilibrium form at P = 50.

Интересной и практически важной является задача определения силы реакции контактного взаимодействия. Составим функцию Лагранжа для задачи (17)—(19) выпуклого квадратичного программирования

Подставляя у(Х) в функцию (X^y(X)), находим

<^(А) =-(Q ¹ (А^тX-\-дД А^т X-\-д)—

— (Q 1 (АтX-\-дД д) — (Q г(АтХ + дД Ат X) +

+(А,Ь) = |(Q-^^TA^^TA) + (Q-^^TA,y) + Л^у-Чу) - ^^ХА^тХ,д^ - (Q^^.y) -

-(Q-¹ Л^ТА, Л^ТА) - (AQ-^Xg, А) + (А, Ь\ (22)

М

(А; у) = V (^-.РР^^+У Х^а^у^ЬДр^а^

Обозначим через А = (Aq, Ai, ..., Хм) Е Н^м^.

Решение задачи (17)-(19) обозначим через у*. Для того, чтобы точка у* была решением задачи необходимо и достаточно, чтобы нашелся множитель Лагранжа А* такой, что точка (А*, у А была седловой точкой функции Лагранжа на множестве Р^2п х А,

(А,у*) < (А*,у*) < (А*,у)         (20)

Чу е Р^2п, А е А,

Компоненты вектора A(Ai,..., Хм) и являются силой реакции контактного взаимодействия кольца и жесткого основания. Графики сил реакции приведены на рис. 6.

А — {(Ao, Ai,..., Хм)^ Xj > 0, j € 1 : МД

Из (20) следует, что

(Х*,уД = max min ^у АеА _уеН^

<\у)

= min max(A,v), уЕН^ АеА ^{4 у}

те. операции взятия max и min в данном случае перестановочны.

Введем в рассмотрение матрицу А, строками которой являются векторы (ао,«1, ..^ам)^ диагональную матрицу Q, элементы q^j которой имеют вид qij — 0 при г ^Д— Д д^ = д^^^-^^ = З²^ - I)². вектор b_Qj = 0, з ф и + 1, Ь_й^. = -2тгДР^1| Ъ = (Ьо,^,..., Ь_М1

Функция Лагранжа в этих обозначениях определяется формулой

(А, у) = |(Qy,y) + (у, у) + (Лу, А) + (Х,Ь), где ^n+i = —2тгРР, gi = 0 при г ^ п + 1.

Решение задачи min (А, у) yeR2n

(с)

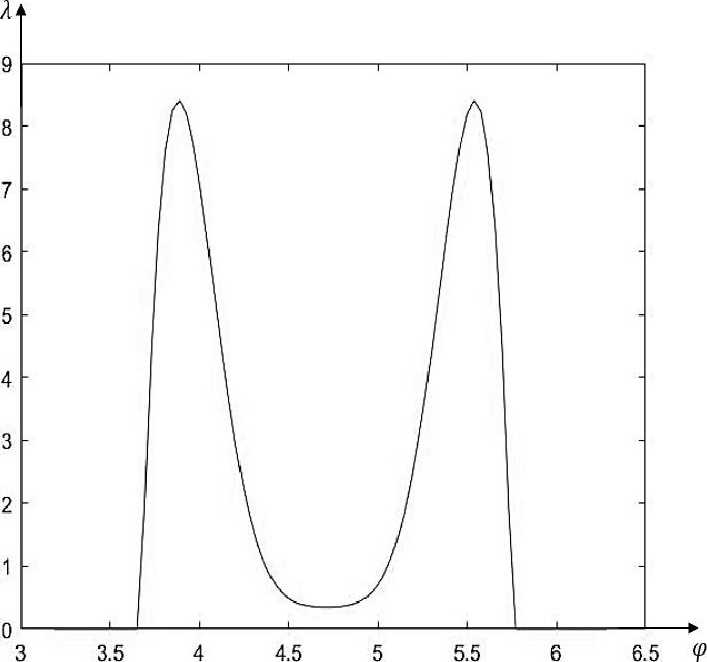
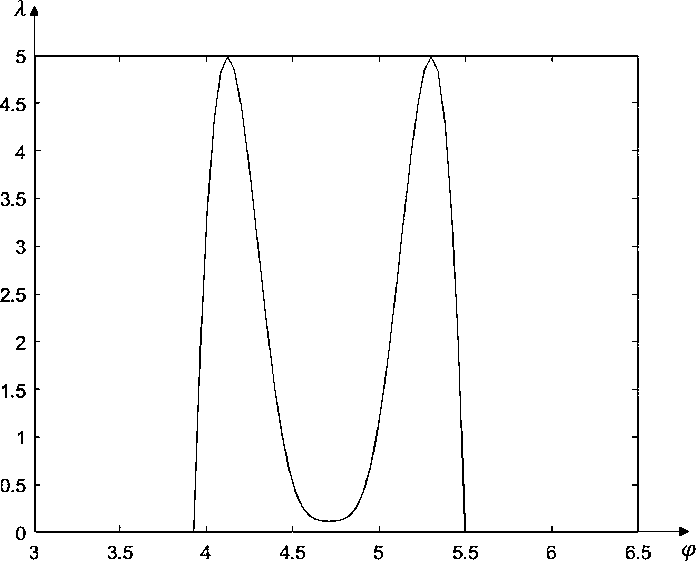
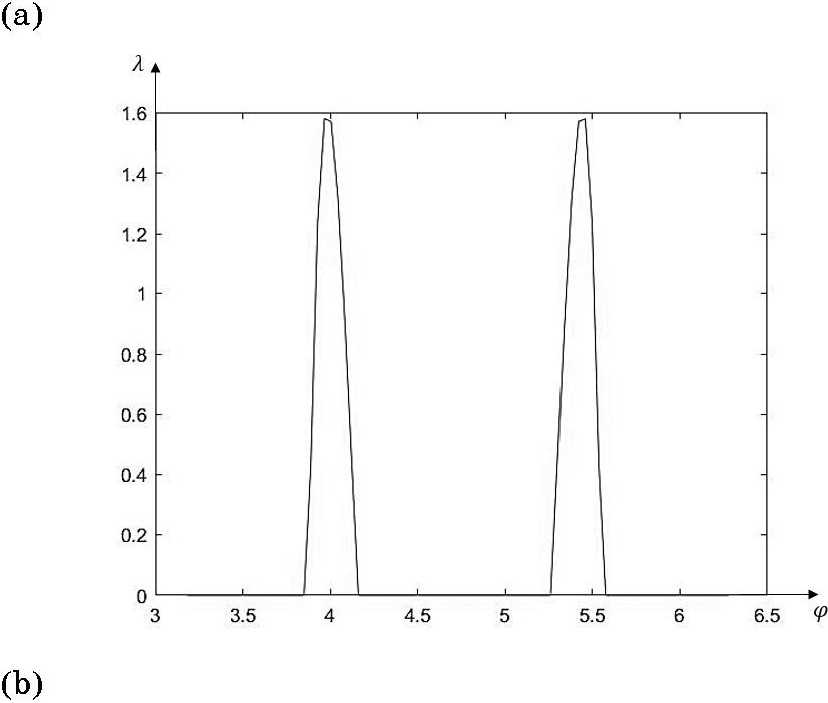
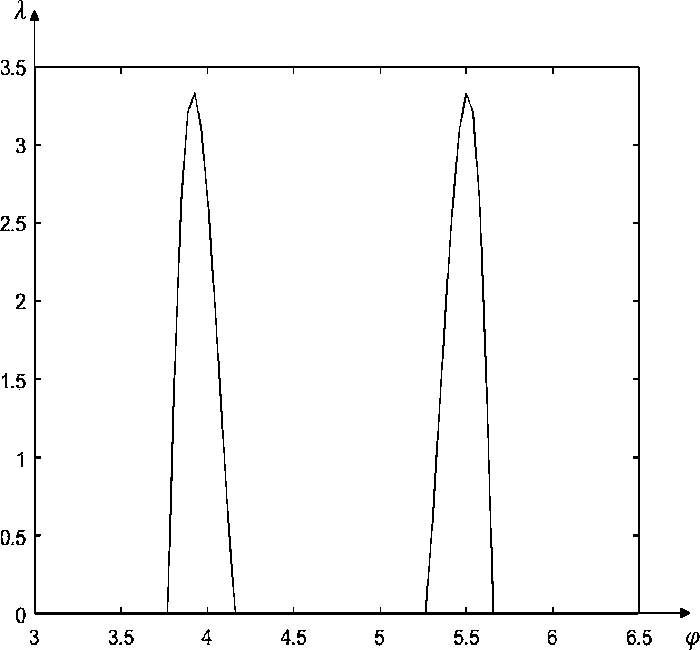
Рис. 6. Графики силы реакции: (а) - при Р = 20; (Ь) — при Р = 30; (с) — при Р = 40; (d) — при Р = 50.

Fig. 6. Reaction force graphs: (a) — at P = 20; (b) — at P = 30; (c) - at P = 40; (d) - at P = 50.

Интересной особенностью задачи является то, что силы реакции контактного взаимодействия носят сосредоточенный характер, т.е. кольцо в окрестности точки Q = ^ отходит от препятствий.

(d)

В данной работе рассмотрена контактная задача кругового кольца и жесткого основания. Ее решение сводится к решению задачи квадратичного программирования. При решении двойственной задачи были определены силы реакции контактного взаимодействия.

• 1.    Михайловский Е. И., Тарасов В. Н. О сходимости метода обобщенной реакции в контактных задачах со свободной границей // Прикладная математика и механика. 1993. Т. 57. Вып. 1. С. 128-136.

• 2.    Панагиотопулос П. Неравенства в механике и их приложения. Выпуклые и невыпуклые функции энергии. М.: Мир, 1989. 494 с.

• 3.    Тарасов В. Н. Методы оптимизации в исследовании конструктивно-нелинейных задач механики упругих систем. Сыктывкар: Коми научный центр УрО РАН, 2013. 238 с.

• 4.    Николаи Е. Л. Труды по механике. М.: Гостех-издат, 1955. 583 с.

• 5.    Теория ветвления и нелинейные задачи на собственные значения // Под ред. Дж. Б. Келлера и С. Антмана. М.: Мир, 1974. 254 с.

• 6.    Тимошенко С.П. Устойчивость упругих систем. М., Л.: ОГИЗ. Гос. изд-во технико-тео-рет. лит., 1946. 532 с.

• 1.    Mikhailovsky ЕЛ., Tarasov V.N. О skhodimosti metoda obobshennoi reaktsii v kontaktnykh zadachakh so svobodnoi granitsei [On the convergence of the generalized reaction method in contact problems with a free boundary] // Applied mathematics and mechanics. 1993. Vol. 57. Issue 1. P. 128-136.

• 2.    Panagiotopulos P. Neravenstva v mekhanike i ikh prilozheniya. Vypuklyye i nevypuklyye funktsii energii [Inequalities in mechanics and their applications. Convex and non-convex energy function]. Moscow: Mir. 1989. 494 p.

• 3.    Tarasov V.N. Metody optimizatsii v issledovanii konstruktivno-nelineynykh zadach mekhaniki uprugikh sistem [Optimization methods in the study of constructive-nonlinear problems of elastic systems mechanics]. Syktyvkar: Komi Science Centre, Ural Branch, RAS, 2013. 238 p.

• 4.    Nikolai E.L. Trudy po mekhanike [Transactions on mechanics]. Moscow: Gostekhizdat. 1955. 583 p.

• 5.    Teoriya vetvleniya i nelineynyye zadachi na sobstvennyye znacheniya [Branching theory and nonlinear eigenvalue problems] // Ed. J.B. Keller and S. Antman. Moscow: Mir, 1974. 254 p.

• 6.    Timoshenko S.P. Ustoychivost uprugih sistem [Stability of elastic systems]. Moscow, Leningrad: OGIZ. State Publ. House of Techn. and Theoret. Liter., 1946. 532 p.