Контактная жесткость плоского стыка

Под нагрузкой неровности, которые определяют особенности шероховатого слоя, могут находится в упругом, упругопластическом и пластическом состояниях. Кроме номинальной или геометрической площади стыка, следует рассматривать контурную площадь, определяемую волнистостью. Каждая из нагруженных волн деформируется упруго, кроме того имеет место дополнительная деформация шероховатого слоя. Контурное давление найдем по задаваемому номинальному давлению по формуле

Контурное давление определяется с помощью имитационного моделирования [1]. Полагаем, что деформируемые неровности, имеющие сферическое очертание в своей верхней части, находятся в упругом, упругопластическом и пластическом состояниях. В этом случае критическая деформация выступа, соответствующая переходу от упругого состояния к упруго-пластическому, определяется выражением

где r - радиус закругления верхней части выступа; H - твердость по Бринеллю более мягкого материала сопряженных поверхностей; E - приведенный модуль упругости, равный

• 1   1-    1-

• где д- коэффициент Пуассона.

Для оценки деформации шероховатого слоя используем фрактальные представления о поверхности твердого тела. Профиль поверхности опишем функцией Вейерштрасса-Ман-дельброта [2,3,5] ∞

• - to = c- ■>"'■"• (      )

где z ( x ) - высота профиля; D - фрактальная размерность профиля (1< D <2); у - скейлинговый параметр для определения спектральной плотности (y>1); G -высотный скейлинговый параметр, не зависящий от частоты; Y ⁿ i =1/L, где L - длина выборки профиля.

Фрактальный параметр G в зависимости от выборочного значения среднего квадратического отклонения профиля Rq будет равен

г

-

Параметр G по данным Д. Павелеску и А. Тудора [4] изменяется в пределах от G= 9,9^10 ¹⁶ до 1,2^10² мкм. Радиус закругления верхней части неровности в соответствии с моделью А. Маджумдара [2, 5] равен

₁ /

^Т = d ²z | =тг ² G^D ~ ¹

При известных данных Rq и г можно определить фрактальные параметры рассматриваемой поверхности G и D .

Модель Маджумдара в отличие от модели Гринвуда-Вильямсона (Г-В) принимает критерий перехода в следующем виде: при деформации, превосходящей критическую 8 >  8_СТ, имеет месс-то соотношение площадей пятен контакта а <  а_ст . Модель Маджумдара предполагает, что все малые пятна (субшероховатость) в начале деформируются пластически, а затем по мере увеличения нагрузки соседние пятна, сливаясь друг с другом, создают такую площадь выступа, которая деформируется упруго. Профиль фрак-тального выступа обычно описывается косину-соидой, верхняя часть которой представляется в виде сферы с радиусом, зависящим от степени «изрезанности» профиля (рис. 1.).

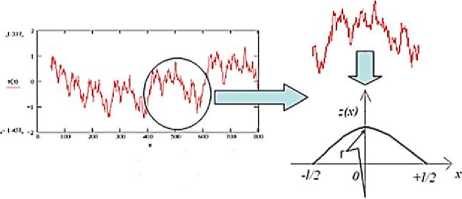
Рис. 1. Модель выступа фрактального профиля

Высота отдельно взятого выступа определяется выражением

(х = 0) = h = G^D" ¹ 1 ² " ^D.

Пусть площадь основания выступа на уровне средней линии равна a_ь = 2urh, а площадь среза на уровне 6 от вершины выступа а = 2лт 8. Так как a_b = it Q) , то а_ъ = у- Тогда

Соотношение

4 a ℎу

=         ․ между  высотой деформацией δ имеет вид

2-D выступа и

4 a ℎ\ 2 "Us")

ℎ= G⁰"¹

Анализ полученного выражения при G=const и h=const, показывает, что отношение должно быть постоянным. Тогда критерий перехода от упругого состояния к пластическому происходит при деформации 5 >   , что соответствует a> CLCr ․ Таким образом, если пло-щадь пятна контакта будет больше, чем кри-тическое значение, то пятно находится в упруго-пластическом состоянии.

Единичный контакт. Для единичного упругого контакта запишем основные соот-ношения

4    1 3

F_e = E Г282 , 8 ≤   ․

Подставив значение радиуса в формулу Герца и, учитывая соотношение 6 =  , получим

F_{e =} 4√ -EG^D"4 ⁽ 3-D )⁄ ² , 0< a < &ecr ․

На рис. 2 показано взаимодействие неровности в виде сферического сегмента с жесткой плитой и с упругим полупространством. Упругопластический контакт характеризуется следующим приближенным соотношением z        \   - ^ecr           .    -

Fep =   + Vp - ^Fe)         _, d_eCT ≤ a ≤ a_p ․

^P - &ecr

Для пластического состояния контакта имеем F_p =    , Cl > dp ․

Множественный контакт. Для множественного контакта используем размерное распределение площадей пятен контакта относительно площади наибольшего пятна aL [5]. Число пятен контакта, имеющих площадь, которая превосходит а , равно

D

N ( a_L > a )=      ․

Тогда размерное распределение площадей пятен контакта (по модулю) имеет вид dN D a° /2

()=    =    (D + 2)/2․ det 2  (    )/

Нагрузка, воспринимаемая всеми пятнами контакта, определяется выражением

Г aecr

F =        ( a' )n( a' ) с!^ +

+ ∫ ^ecr^P ( a ′)n( a ′) с!^ +∫ ^{∞ F}P ( a ′)n( a ′) с!^ ․    (1)

Критерии перехода от одного вида деформации к другому (от упругого к упругопластическому и к пластическому)      выражаются      следующими зависимостями [6]:

Q-ecr = 2,4 TIT² ( H ⁄ E )²; a_p = 5,35 ЛГ² ( H ⁄ E )²․

Для количественной оценки в качестве примера используем экспериментальные данные сочетания, для которого эффективный радиус за-кругления верхней части неровности ^*eff = 50 м км ; Raeff =1,76 мкм. Примем в соответствии с [6] Rq eff = JI ^R-ff = 2,2 мкм. Для фрактального профиля поверхности найдены значения частот ^min =2∙10 ³ мкм и       ⁼

0,125 мкм. Тогда фрактальные параметры определим, решая систему уравнений

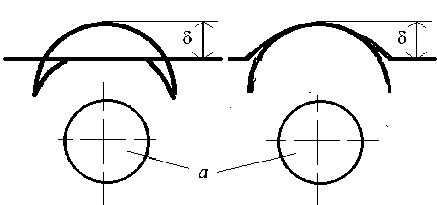
Рис. 2. Площади упругого контакта: деформируемая неровность и деформируемое полупространство

устная: - ^min aD/2

T = —-—z:— r. ⁼         ․

Для рассматриваемого сочетания получены D =1,214 и G =8,758 ∙ 10^-9 мкм=8,758 ∙ 10^-12мм. Приведем в табл. 1 экспериментальные и расчетные данные, характеризующие зависимость сближения от давления при первом нагружении для рассматриваемого сочетания.

Таблица 1. Зависимость сближения от давления

Сближение, мкм	Давление (номинальное), МПа
	3	6	9	12	15
первое нагружение (эксперимент)	1,8	4,4	6,7	7,5	8,1
сближение за счет волнистости (расчет)	0,6	0,8	1,0	1,2	1,4
деформация шероховатого слоя (эксперимент + расчет)	1,2	3,6	5,7	6,3	6,7

Нормальная удельная контактная жесткость шероховатого слоя. Рассмотрим некоторые методы оценки контактной жесткости плоского стыка с шероховатыми поверхностями.

• 1.    Метод, основанный на анализе экспериментальных данных (табл. 1). Зависимость деформации от давления в плоском стыке представлена на рис. 3. Прямая линия представляет собой уравнение регрессии

  p = 1․936 6 ․

• 2.    Аналитический метод. В основу метода

Контактная жесткость шероховатого слоя плоского стыка равна dp      МПа d8 = ,936 мкм․

Knr

положена зависимость (1), в которой переменной величиной принята максимальная площадь пятна Ct_L . Эта максимальная площадь определяет деформацию наибольшего выступа. Связь деформации и площади приведена для рассматриваемого сочетания в табл. 2. Номинальная площадь контакта Аа принята равной 0,6 мм². На рис. 4 представлены зависимости давления от деформации шероховатого слоя плоского стыка.

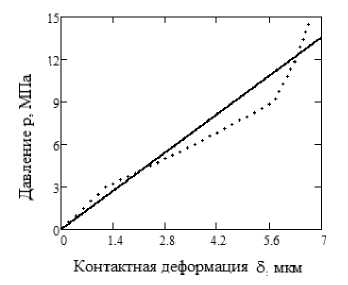
Рис. 3. Зависимость контактного давления от деформации

Уравнение регрессии фрактальной модели имеет вид

= 1,373  + 1․254․

Контактная жесткость шероховатого слоя равна

МПа

=1,373 _мкм ․

Сравнение анализируемых моделей показало их близкое соответствие. Следует отметить, что для данного сочетания зависимость деформации от давления носит линейный характер, и контактная жесткость шероховатого слоя плоского стыка является постоянной величиной.

Рассмотрим другое сочетание стальных поверхностей, для которого эффективные параметры шероховатости были следующими: R a еff = 1,23 мкм; r еff = 37 мкм; r w eff = 2242 мкм. В табл. 3 приведены расчетноэкспериментальные данные, отражающие связь давления с деформацией стыка и выделенной деформацией шероховатого слоя , мкм.

Таблица 2. Основные параметры контактного взаимодействия

Деформация шероховатого слоя   , мкм	Площадь наибольшего пятна а, мм2	Нагрузка F , Н	Контактное давление р = F/Aa, МПа
1,5	2,356 ∙ 10-4	2,6	4,3
2,0	3,142 ∙ 10-4	2,9	4,8
3,0	4,712 ∙ 10-4	3,4	5,7
4,0	6,283 ∙ 10-4	3,9	6,5
5,0	7,854 ∙ 10-4	4,5	7,5

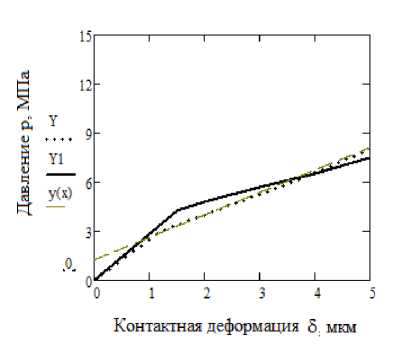
Рис. 4. Зависимость «давление ‒ деформация»: Y ‒ эксперимент; Y1 ‒ фрактальная модель; y(x) ‒ уравнение регрессии модели

Уравнение регрессии фрактальной модели

имеет вид

= 1,373  + 1․254․

Контактная жесткость шероховатого слоя равна

МПа

=1,373 _мкм ․

Сравнение анализируемых моделей показало их близкое соответствие. Следует отметить, что для данного сочетания зависимость деформации от давления носит линейный характер, и контактная

жесткость шероховатого слоя плоского стыка является постоянной величиной.

Приняв R q =1,54 мкм, найдем для рассматриваемого сочетания D=1,195 и G=1,367 ∙ 10^-13 мм. Эти фрактальные параметры были применены для получения количественной оценки контактной жесткости

рассматриваемого плоского стыка.

Таблица 3. Зависимость деформации от давления

Параметр	Давление в стыке р , МПа
	3	6	9	12	15
деформация стыка	3,6	5,8	8,1	9,8	11,2
деформация шероховатого слоя	3,0	5,0	7,1	8,1	9,8

На рис. 5 (а) приве-дена зависимость «давление ‒  деформация»,   получен-ная   на основании экспериментальных данных и здесь же построена кривая уравнения регрессии. Уравнение регрессии имеет вид

=0․798  ^․ .

Нормальная контактная жесткость шероховатого слоя для данного сочетания по экспериментальным данным определяется выражением = 1․037   ^․ ․ .

График зависимости контактной жесткости от номинального давления показан на рис. 5б. Обращает на себя внимание тот факт, что до давления, равного 4 МПа, эксперимент и расчет находятся в хорошем соответствии, а после этого давления наблюдается расхождение данных, полученных экспериментально и расчетом.

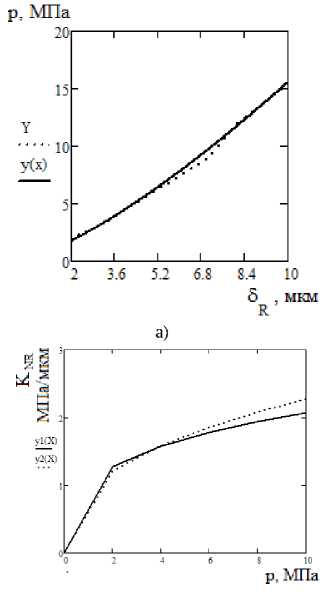
б)

Рис. 5. Механическая характеристика стыка: а) зависимость «давление ‒ деформация», б) зависимость нормальной контактной жесткости от нагрузки (давления): сплошной линией показан эксперимент, пунктирной – модель

Расхождение растет с увеличением давления. Этот факт подтверждается и исследованием Х. Янга. В работе [7] приведены данные о контактной жесткости плоского стыка стальных поверхностей, имеющих следующие физико-механические и фрактальные параметры: H =1960 МПа; G =5 ∙ 10^-11мм; модуль упругости E 1 =E 2 = 2,07 ∙ 10⁵ МПа; коэффициент Пуассона μ 1 =μ 2 =0,29. Янг отмечает, что до 1,2 МПа экспериментальные данные совпадают с расчетом. При увеличении давления в стыке наблюдается расхождение теории с экспериментом, причем это расхождение также растет с увеличением давления.

Определенный интерес для случая преимущественно упругого контакта представляют работы [6, 8]. Для отдельно взятой фрактальной неровности контактная жесткость определяется следующей упрощенной зависимостью

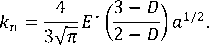
где Е ^∗ ‒ эффективный модуль упругости; а ‒ площадь пятна контакта.

При оценке контактной жесткости стыка (множественный контакт) в работе [6, 8] использовалось размерное распределение пятен контакта, предложенное А. Маджумдаром [5]. В этом случае контактная жесткость стыка, выражаемая в Н/мм, определяется выражением

CaL

К ^∗ NR =        ( а ′) da ․

Здесь максимальная площадь пятна контакта не должна превышать критическое значение, соответствующее переходу от упругого состояния к упругопластическому. Модель имеет ограниченное применение, так как не рассматривает упругопластическое и пластическое состояние пятен касания. Произведя интегрирования с учетом выражений для k„ и размерного распределения пятен контакта, авторы работы [6, 8] получили следующее уравнение

(3- Ds )( Ds -1) (2- D_s ⁾²

iz ∗= ______г ∗

^{NR =}3√2 к

^aL ․

Дадим оценку контактной жесткости шерохо- ватого слоя по этой формуле. Пусть, как в предыдущем случае, D=1,195; aL = ∙0․037∙0․001=1,162∙ 10 4 мм 2 ․ Тогда контактная жесткость шероховатого слоя оказывается равной к∗ NR = 311,4 Н/мм = 0,31 Н/мкм.

Отсутствие значения номинальной площади в предложенных зависимостях не позволяет дать оценку удельной контактной жесткости.

Выводы:

• 1.    Из общей деформации стыка выделена дефор-

• мация шероховатого слоя.

• 2.    Приведена методика определения удельной контактной жесткости плоского стыка как фрактального объекта.

• 3.    Определены фрактальные параметры приведенной поверхности за счет замены контакта двух шероховатых поверхностей на контакт гладкой поверхности с шероховатой, имеющей эффективные параметры. Оценка фрактальных параметров D и G произведена путем решения системы уравнений, содержащих эффективные параметры шероховатости, измеренные в соответствии с ГОСТ 2789-73.

• 4.    Показано влияние фрактальных параметров и установлены закономерности изменения удельной контактной жесткости от номинального давления. Приведены соответствующие примеры.

• 5.    Выявлено, что удельная контактная жесткость разных сочетаний плоского стыка по разному зависит от параметров, характеризующих шероховатость и от давления. Представление о шероховатом слое как о фрактальном объекте позволило разработать общую методику определения контактной жесткости разных сочетаний поверхности элементов плоского стыка.