Контактное взаимодействие котла вагона-цистерны с лежневыми опорами

доработке. В тоже время не установлено убедительных причин эксплуатационного разрушения элементов лежневой опоры, стяжных хомутов, лап крепления котла к хребтовой балке.

Развитие численных методов решения систем дифференциальных уравнений, совершенствование вычислительных технологий и стремительный рост возможностей современных ЭВМ позволяют с высокой точностью определить поле напряжений в деталях сложной формы в пределах упругих деформаций. Проблема здесь кроется в корректной постановке граничных условий, определяемых контактным взаимодействием элементов сложной конструкции. Повышение точности решения контактной задачи опоры котла на лежневую опору имеет целью предотвратить, прежде всего, разрушение обечайки. Разрушение деревянных брусков (или полиуретановых прокладок) между оболочкой и опорой не является предельным состоянием конструкции в целом. Но последующее ослабление крепежных хомутов приводит к динамическим нагрузкам и разрушению хомутов и крепежной лапы, приваренной к днищу котла и соединяющей его с хребтовой балкой [5]. Необходимо решить контактную задачу, чтобы корректно описать передачу нагрузки от котла на лежневые опоры, оценить прочность прокладочных элементов и найти возможную локализацию напряжений в цистерне, которая может определять ресурс всей конструкции.

В работе [ 4 ] в одномерной постановке решена контактная задача моделирующая передачу нагрузки от котла вагона-цистерны на лежневые опоры. При решении использовался метод контактных элементов, который широко применяется при решении контактных задач для оболочек вращения, взаимодействующих с упругими или жесткими основаниями [ 6 ] .

В работе [ 4 ] определена одномерная область контакта и распределение по ней контактных усилий, а затем напряженное состояние и долговечность оболочки.

В предлагаемой работе задача обобщается на двумерную область контакта. Таким образом, задача состоит из определения двумерной области контакта для тонкой оболочки, лежащей на сплошном основании, и определения распределения контактных усилий. Предлагаемая задача имеет как прикладное значение – определяются контактные усилия в двумерной области для реальной конструкции котла вагона-цистерны, которые влияют на напряженное состояние всей конструкции, так и фундаментальное значение – разработанный ранее численный метод контактных элементов применяется для новой задачи.

Представим срединную поверхность котла вагона-цистерны в виде оболочки вращения, лежащей на жестком основании (рис. 1). Между оболочкой и основанием имеется упругая прокладка. Координатную поверхность оболочки вращения отнесем к криволинейной ортогональной системе s, θ , где s – длина дуги меридиана, θ – центральный угол в параллельном круге. Линии s=const , θ=const являются линиями главной кривизны. Воспользуемся классической теорией оболочек, основанной на гипотезах Кирхгофа-Лява. В этом случае задача определения напряженного состояния оболочки описывается системой дифференциальных уравнений в частных производных [ 6, 7]:

dY .4        dmY

----=/ A_m ( s, 0 ) --+ f ( s, 0 ) ,        (1) d s £ o ^mV   ’em™

Y = ,N. Nz S Ms Ux Uz v 0s {        ,        , ,         , , , , }, где Nr, Nz – радиальное и осевое усилия; ur, uz – аналогичные перемещения; S$ - сдвигающее усилие; Ms – меридиональный изгибающий момент; v - окружное перемещение; ^s - угол поворота нормали. Элементы матрицы Am зависят от геометрических и механических характеристик оболочки.

Раскладывая компоненты внешней нагрузки и искомые функции в системе (1) в ряды Фурье по окружной координате θ и разделяя переменные для каждого члена разложения, имеем разрешающую систему обыкновенных дифференциальных уравнений восьмого порядка [6, 7]. Добавляя граничные условия, данная система может быть проинтегрирована численно. Решение задачи состоит в нахождении распределения контактного давления между оболочкой и основанием q(θ,s) в зависимости от окружной координаты, определяемой углом 0 и меридиональной координаты s, и области контакта Ω+(θ,s). При изменении внешней нагрузки P (вес оболочки и груза, избыточное давление и др.) в силу упругости оболочки область контакта Ω+ может изменяться. Возможно также образование зон отставания в меридиональном и окружном направлениях.

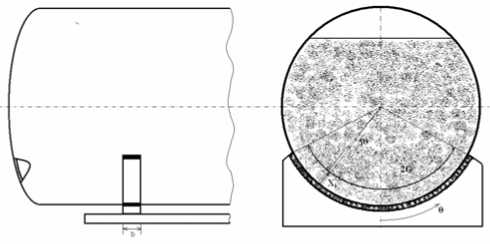
Рис. 1. Срединная поверхность котла вагона-цистерны

При решении рассматриваемой задачи с неизвестной границей области Ω + , необходимо искомую область дополнить областью Ω ^ до некоторой известной области Ω. Следовательно,

Q = Q+ +Q

где Ω – физически допустимая область контакта. При этом

Q = 2 tfl х b m где 2tθ и b – максимальные размеры области контакта в окружном и меридиональном направлениях.

Проведем дискретизацию области Q (NxK) прямоугольными криволинейными элементами (N, K – число элементов по окружности и меридиану). Для этого область Q разобьем на участки в меридиональном направлении, а полученные кольца разделим на одинаковое количество элементов по окружности. На каждом полученном элементе примем постоянное значение контактного давления q≥0. Следовательно, взаимодействие между оболочкой и основанием можно представить определенным количеством усилий Xiy, приложенных на каждом элементе qj = XyA-1, i = 1...N, j = 1...K, где A=aθ x as (aθ, as – линейные размеры по окружности и меридиану) – площадь контактного элемента.

Для определения усилий взаимодействия используем классический смешанный метод строительной механики [ 7 ] . Учитывая наличие упругой прокладки между оболочкой и основанием, уравнения для первого кольца будут иметь вид [4, 6]

N

У ^ X ( 1 ) - Z ^{( 1 )} cos O + DX ^ = 0 1 i i                                    1                  1

i = 1

N

Z ⁸ * ^ХТ" Z "' cos". + DX« = 0

i - ¹                                                       (2)

N

Z cos O X¹ = P ^{( 1 )} .

i = 1

Здесь δ ij – перемещение в основной системе координат по направлению i связи от единичного усилия, введенного по направлению отброшенной j связи; Z cos θ i – перемещение в основной системе по направлению отброшенной i связи, происходящее от единичного перемещения по направлению введенной связи; X i – неизвестные усилия взаимодействия. В системе (2) индекс в скобках обозначает номер кольца, P P ⁽¹⁾ – нагружение первого кольца.

В системе (2) D есть оператор, связывающий реактивное усилие i точки поверхности прокладки и ее перемещение. Оператор D является аналогом параметра регуляризации, применяемым в аналитических методах решения контактных задач теории оболочек [ 8 ] . Для рассматриваемой задачи будем использовать простейшую модель линейно-деформированного основания (прокладки) – модель Винклера, и следовательно

D = —

CA где C – коэффициент постели.

Податливость оболочки δij в системе (2) определяется от единичного усилия, действующего на каждом контактном элементе. Поскольку у нас исследуется двумерная область, то учтем влияние оставшихся К-1 колец на первое, как это делается при решении двумерных задач [7, 9] и найдем искомое распределение давлений на площадке контакта котла с опорой. Поскольку возможны отставания оболочки от основания, то затем необходимо применять итерационные процедуры поиска реальной области контакта, которая зависит от геометрических и упругих параметров конструкции и величины нагрузки P [6, 7, 9].

С использованием предлагаемого подхода рассмотрено контактное взаимодействие цилиндрической части оболочки котла вагона-цистерны, лежащей на опорах (рис. 1). При расчете принимались – внешний радиус цилиндрической оболочки R=1,50 м, радиус основания R=1,50 м, толщина стенки h=0,06 м, модуль упругости E=2,1x105 МПа, коэффициент Пуассона v =0,3. Главный вектор внешней нагрузки, действующий на опору, приложен вертикально и равен P=4,5x105 Н. Оболочка лежит на жестком основании, расположенном симметрично относительно контуров шириной b=0,25 м. Длина основания вдоль окружной координаты 2tθ стягивается углом 120o. Между основанием и оболочкой имеется прокладка. Граничные значения коэффициента постели C=(108-1011) Н/м3 характерны для вакуумной резины и абсолютно жесткого основания. Граничные условия приняты в виде жесткого защемления по обоим контурам ux = Uz = v = Os =0 (s = s 0, SL )

На рис. 2 показано распределение контактного давления q по области Ω. Длина области контакта 2 t θ разбивалась углами равными AO =2 ° ( N =60). Длина области контакта в меридиональном направлениях b=0,25 м делилась на пять контактных элементов ( K =5). Для лучшего восприятия распределения контактного давления q по области Ω рисунок сделан с увеличенным в 5 раз размером контактного элемента a s . Упругие свойства основания – прокладки (C=10⁸ Н/м³ позволяют получить достаточно плавное распределение контактного давления q по всей области Ω. При повышении жесткости основании в тысячу раз (С=1011 Н/м³) можно считать, что контакт происходит с абсолютно жестким основанием. Данный расчетный случай показан на рис. 2. На рисунке видно наличие на границе области контакта локальных сил, что соответствует классическим решениям теории контактных задач для оболочек [ 9 ] . Наличие таких локальных сил может определять прочность и устойчивость оболочечных конструкций, и, следовательно, в этом месте может зарождаться усталостная трещина, которая будет определять общий ресурс конструкции.

Дискретная опора оболочки в виде деревянных брусков меняет характер распределения давления, но максимальное значение в крайних брусках не превышает 3 МПа. В испытаниях на сжатие сосновых брусков попе- рек волокон разрушающее давление составляет по нашим данным 6-8 МПа, следовательно, статическая прочность брусков обеспечена. В эксплуатации бруски выдерживают также нагрузки, связанные с вертикальной динамикой и движением в кривых, а имеющиеся случаи разрушения носят усталостный характер. Для определения долговечности прокладок нужны натурные усталостные испытания при параметрах цикла давления, определенных решением контактной задачи.

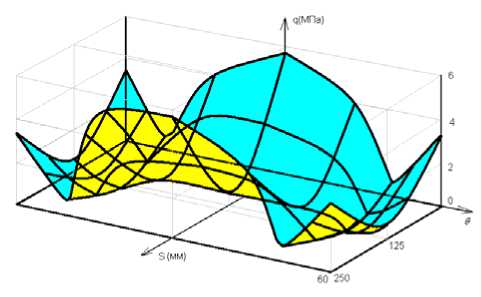
Рис. 2. распределение контактного давления q по области Ω

Вывод: предложенный подход, позволяющий решить контактную задачу, моделирующую передачу нагрузки от котла вагона – цистерны на лежневые опоры, позволяет уточнить распределение контактных усилий и оценить прочность прокладок.